基于动态聚类的文档碎纸片自动拼接算法
尹玉萍,刘万军,张 冲,刘永超
YIN Yuping1,LIU Wanjun2,ZHANG Chong1,LIU Yongchao1
1.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105
2.辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105
1.School of Electrical and Control Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China
2.School of Software,Liaoning Technical University,Huludao,Liaoning 125105,China
1 引言
碎纸片自动拼接技术是图像处理与模式识别领域中的一个较新但是很典型的应用[1],它是通过扫描和图像提取技术获取一组碎纸片的形状、颜色等信息[2-4],然后利用计算机进行相应的处理从而实现对这些碎纸片的全自动或半自动拼接还原[5-7]。二维碎纸片自动拼接问题主要有两种解决方案:基于轮廓的拼接和基于内容的拼接[8]。前者类似的研究较多一些,例如罗智中提出的基于线段扫描的碎纸片边界检测算法研究[9],高剑,张彩明,孟祥旭,冯志全提出的一种基于DDTW的三维碎片自动拼接方法[10],朱延娟,周来水,刘毅提出的二维非规则碎片匹配的算法[11],刘金根,吴志鹏,刘上乾,殷世民提出的一种基于特征区域分割的图像拼接算法[12]等等。目前,对于基于内容的文档拼接研究的论文还比较少,但还是有一些,例如罗智中提出的基于文字特征的文档碎纸片半自动拼接[13]等。在碎纸拼接技术中,从目前的研究现状来看,虽然很多的文献都在这方面做了大量的研究工作,但是迄今为止,仍然没有很成熟的方法应用于相关工作中。
为此,本文主要针对碎纸机撕碎纸片的三种形式进行自动拼接和复原,即分别对仅纵向碎纸条、横纵向均进行碎纸的单面碎纸块和横纵向均进行碎纸的双面碎纸块,开展基于动态聚类的文档碎纸片自动拼接算法研究。(1)首先利用定义的行匹配度矩阵解决仅纵切问题。(2)在横纵向均进行碎纸的单面碎纸块的拼接问题中,首先求出所有碎纸片的特征向量,以特征向量为聚类依据进行动态聚类,初步找出哪些碎纸片属于同一行,然后再根据碎纸片的特征线进行动态聚类的后期处理,确定出最终的行分类,以及行间排序。利用定义的行匹配度矩阵和列匹配度矩阵,结合提出的动态聚类的四邻近拼接算法,匹配出每一行碎纸片的行内排列顺序,最后得到整篇文档的拼接结果。(3)对于横纵向均进行碎纸的双面碎纸块的拼接问题中,在解决第二种碎纸片问题的基础上,求出行分类和行间排序后,考虑到正反两面均有匹配信息,将待匹配碎纸片的正反面匹配度平均值作为匹配依据,根据动态聚类的四邻近拼接算法进行拼接。实验表明,该方法参数少实现简单有效,能快速得到上述三种碎纸片的拼接复原结果。
2 匹配度矩阵
为了能有效地找出对应于原文档的相邻碎纸片,将每一个碎纸片的像素矩阵进行黑白二值化处理转化为(0-1)矩阵,当像素点是白色时该位置赋值为0,否则该位置赋值为1,并由此定义行、列匹配度矩阵如下。
定义1若将原文档碎成m×n块碎片,则行匹配度矩阵记为 Match1=(mij)m×n,其中

行匹配度矩阵元素mij主要体现了碎纸片i的右边缘与碎纸片 j的左边缘的匹配程度。
定义2若将原文档碎成m×n块碎片,则列匹配度矩阵记为 Match2=(nij)m×n,其中

列匹配度矩阵元素nij主要体现了碎纸片i的下边缘与碎纸片 j的上边缘的匹配程度。
3 基于碎纸片特征向量的动态聚类的行聚类
3.1 碎纸片特征向量
为了将碎纸片按行进行分类,即将属于同一行的碎纸片归为一类,定义碎纸片特征向量如下:
定义3设每页纸被切为m×n个碎片,每个碎纸片的像素数为r×l,将全部m×n张碎片进行黑白二值化处理后,若第 j个碎纸片的第i行为纯白色行时该行标记vi=0;否则该行标记 vi=1,则称向量 cvj=[v1,v2,…,vr]T为第 j个碎纸片的特征向量,其中 vi∈{0,1},i=1,2,…,r。
第j个碎纸片如图1所示。
其中22是全零行的行数,35是非零行的行数,以此类推得到所对应的碎纸片特征向量为:
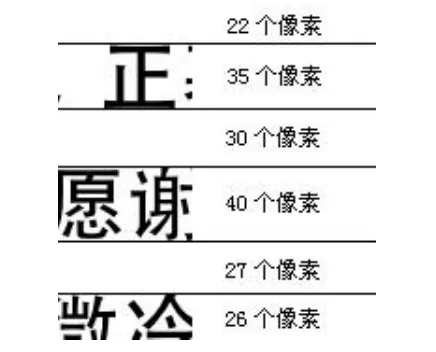
图1 第j个碎纸片
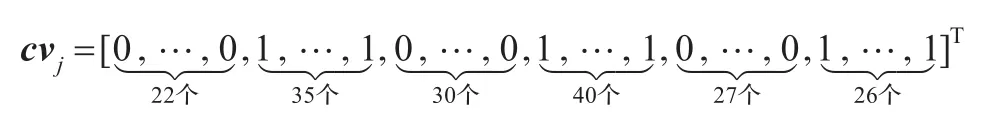
3.2 基于动态聚类的行聚类
由于处于同一行的碎纸片中文字所占位置是相似的,所以文件中属于同一行的碎片的特征向量相似度较大。据此,对所有碎片基于其特征向量进行动态聚类[14-15],初步找出在同一行的碎纸片。设该聚类样本集合为CV={cv1,cv2,…,cvmn},其中 cvj=[v1,v2,…,vr]T为第 j个聚类样本。
动态聚类的行聚类具体算法步骤如下:
(1)选定一个合适的动态聚类阈值γ,原文有m行,所以选取γ的依据为使分类数k大于等于m,且每类包含碎片个数小于等于n。之所以存在k>m的情况是因为考虑到一些特殊的碎片可能不会准确归类问题。并设初始聚类数k=1,聚类重心初始值z1为第一个输入样本。
(2)计算第1个聚类重心与第2个样本之间的距离d21。如果d21>γ,聚类数k=2,第2类的聚类重心为第2个样本;否则第2个样本归于第1类当中。为防止聚类重心飘移对该算法的影响,采取将聚类重心保持不变策略。
(3)依次计算剩下样本与已有的k个聚类重心之间的最小距离dij。如果dij>γ,聚类数为k=k+1,第k+1类的聚类重心为第i个样本。否则,第i个样本就属于第 j类,聚类重心不变。
(4)将所有样本进行聚类完毕后,若k<m,返回步骤(1)。若k≥m,则k即为最后的聚类数,zj(j=1,2,…,k)为对应的聚类重心。
4 动态聚类的后期处理
4.1 聚类检验及调整
如果k=m,检验分类是否正确,即判断每类是否有n张碎纸片,并且同一行碎纸片的汉字中线是否在同一水平线。否则进行如下操作:
(1)将每一类中所有碎纸片看作一个新的碎纸片,根据3.1节的定义3求其特征向量。
(2)求出每一类碎纸片所有完整文字行的中线到碎纸片上边缘的像素数 Sij,i=1,2,…,k;j=1,2,…,jmax,其中 jmax表示第i类碎纸片中完整文字行的行数,为了减少工作量,从第i类碎纸片中第一行完整文字,计算其所占像素数ui,并取第一行完整空白行,计算其所占像素数vi。其中,完整文字行表示该类碎纸片的特征向量两组相邻“0”之间“1”的个数;完整空白行表示该类碎纸片的特征向量两组相邻“1”之间“0”的个数。
然后,将k个类中选出的ui与vi分别取平均值,记为uˉ和vˉ,分别作为整个文档文字字体大小与行间距的平均度量。
例如图1所示碎纸片,假设已按照3.2节方法将其所在的类找出并且该类同图1碎纸片具有两行完整文字,则 jmax=2,Si1=35/2+22=39.5,Si2=40/2+22+35+30=107;ui=35,vi=30。
(3)将第 i类 jmax个 Sij对取余并求平均值,记为,则表示第i类第一行文字的中线与碎纸片上边缘的像素数。
(5)通过图像显示检验分类是否正确,如果存在分类错误的碎纸片,则进行人工干预调整,直至将所有碎纸片分成m行,每行有n张碎纸片。
4.2 行间排序
在4.1节的基础之上,对行与行之间的顺序进行排列。进行如下操作:
(1)将所有碎纸片分成m类后,按3.2节所述步骤(1)~(3)得到每类碎纸片的。
(2)按如下公式判断第i类碎纸片与第 j类碎纸片是否属于相邻行:
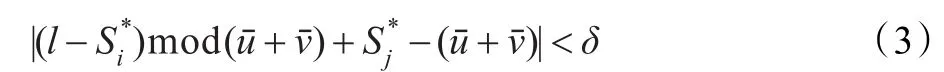
5 基于动态四邻近拼接算法
在已确定所有碎纸片的行分类以及行间排序的基础上,进行碎纸片的拼接,步骤如下:
(1)从第一行中找出处于第一列和最后一列位置的碎纸片,根据Match1矩阵元素的定义和一般文档碎纸片的特点可以得到原文档两个边缘的相应碎纸片,当碎纸片a的右边缘与碎纸片b的左边缘均无文字时,其对应(0-1)矩阵相应的列元素均为0,此时匹配度mab=1,可以以较大概率判断出碎纸片a为最后一列的碎纸片,碎纸片b为第一列的碎纸片,并将两个位置的碎纸片标号存放到碎纸片排序矩阵 pic=(picij)m×n当中。表示如下:

(2)以当前确定好位置的碎纸片排序矩阵 pic为基础,计算所有待匹配区域的四邻近加权匹配度。为了对一般情况进行讨论,以图2中左侧第k次循环的效果图为例进行说明,其中,画斜线阴影的方框表示已放入 pic矩阵的碎纸片,箭头所指空白区域为待匹配区域,例如 pichg表示第h行且第g列位置的待匹配区域所要得到的碎纸片,在第h类未匹配的碎片当中,求出第h行第g列待匹配区域与周边已经匹配完碎片的加权匹配度最大的碎纸片。其中加权匹配度有两种情况:
①待匹配区域与一边相邻,其加权匹配度即为与相邻一侧碎纸片的匹配度。如 pic15所在待匹配区域的位置与左边匹配即可。
②待匹配区域与多边相邻,其加权匹配度即为与各相邻侧已匹配完碎纸片的行列匹配度和上下匹配度的加权平均值,其权重与该边长度成正比。如 pic34、pic22所在待匹配区域的位置。
(3)比较第(2)步中所有已选出的碎纸片四邻近加权匹配度大小,找出最大值对应的碎纸片,并将其添入pic矩阵中。假设 pic15位置的四邻近加权匹配度是最大的,则将其位置填上,如图2右侧第(k+1)次循环的效果图。通过图像显示检验拼接是否正确,如果不正确,暂停程序,并在该行余下的碎纸片中按照匹配度由大到小依次寻找,直到找到正确匹配的碎纸片。如果正确,转下一步。
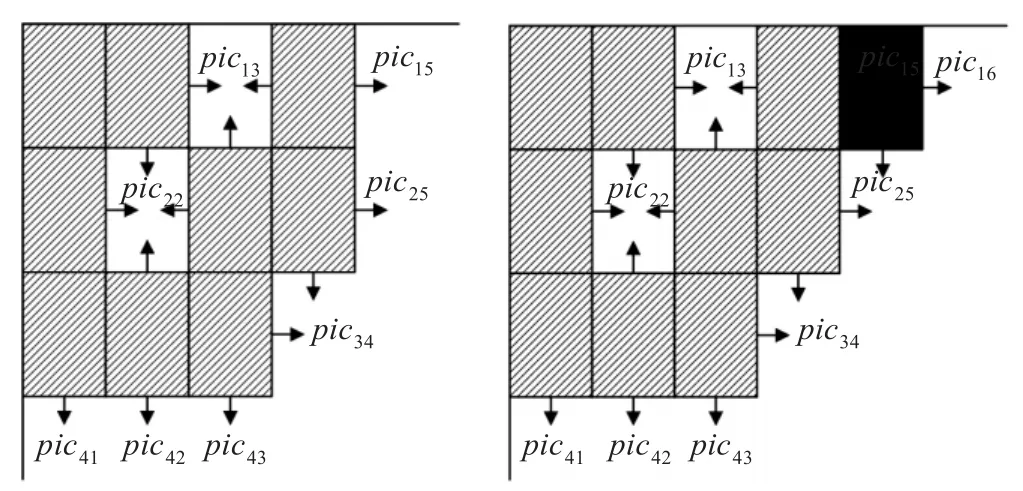
图2 程序第k次循环和第k+1次循环匹配效果图

图3 复原后仅纵向碎纸片拼贴排列序号表
(4)判断所有碎纸片是否均已填入 pic矩阵中,如果没有,返回步骤(2)继续循环,否则循环结束。
6 拼接实验
为检验本文提出的基于动态聚类的文档碎纸片自动拼接算法的可行性和有效性,实验在计算机ThinkPad-SL510k上实践,操作系统是Windows XP,主频2.20 GHz,利用Matlab7.5.0运行程序。本文以2013年“高教社”杯全国数学建模竞赛B题为验证对象。
6.1 仅纵向碎纸条拼接
由于该问题中m=1,n=19为简单问题,属于上述算法的简单特例,具体操作时无需运用动态聚类进行行聚类和行间排序,仅需使用行匹配度矩阵得到如下结果,在匹配过程中没有人工干预,正确率为100%。复原后仅纵向碎纸片拼贴排列序号表如图3所示。仅纵向碎纸片拼贴前后对比图如图4所示。

图4 仅纵向碎纸片拼贴前后对比图
6.2 横纵向均进行碎纸的单面碎纸块拼接
该问题中,m=11,n=19,设动态聚类阈值γ=5,判定两行碎纸片是否相邻的阈值δ=2。利用本文所提算法得到如表1及图5的复原结果,在匹配过程中人工干预12个碎纸片,共209个碎纸片,故正确率为94.3%。

图5 横纵向均进行碎纸的单面碎纸块拼贴前后对比图
6.3 横纵向均进行碎纸的双面碎纸块拼接
此题中同样m=11,n=19,动态聚类阈值γ=5,判定两行碎纸片是否相邻的阈值δ=2,区别于6.2节的是碎纸片是双面的(同一序号分a、b两种,表示同一碎纸片的正反两面),使得碎纸片信息量增大,更方便进行行聚类以及行间排序,在进行基于动态聚类的四邻近拼接时,将碎纸片的正反两面同时进行加权匹配拼接,大大减少了人工干预的几率,得到如图6及图7的复原结果。其中图6的上图为正面的碎片序号排序,图6下图为反面的碎片序号排序,且上图第i行从左到右的顺序为这一行的正面碎片排序,下图为上图的左右180°翻转,且碎纸片进行相应翻转(即序号不变,a、b互换),得到其反面排序,例如图6上图中,第2行第2列的152b翻转得到下图的第2行第18列的152a,它们是原文当中同一个碎纸片的正反面。在匹配过程中人工干预9个碎纸片,共209个碎纸片,故正确率为95.7%。
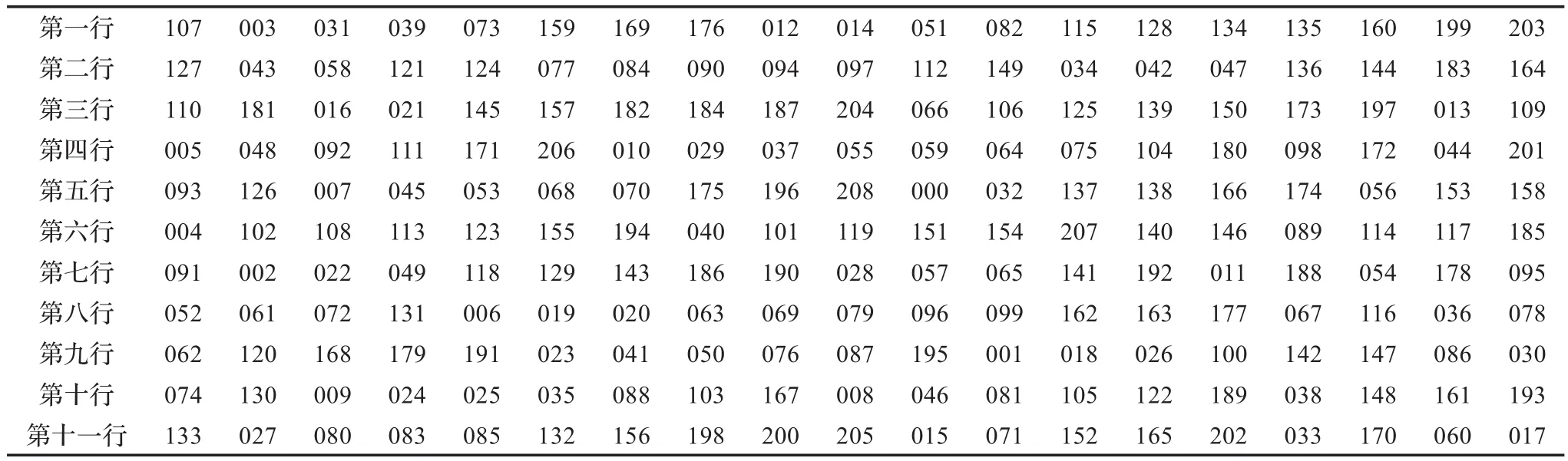
表1 复原后横纵向均进行碎纸的单面碎纸块拼接序号表
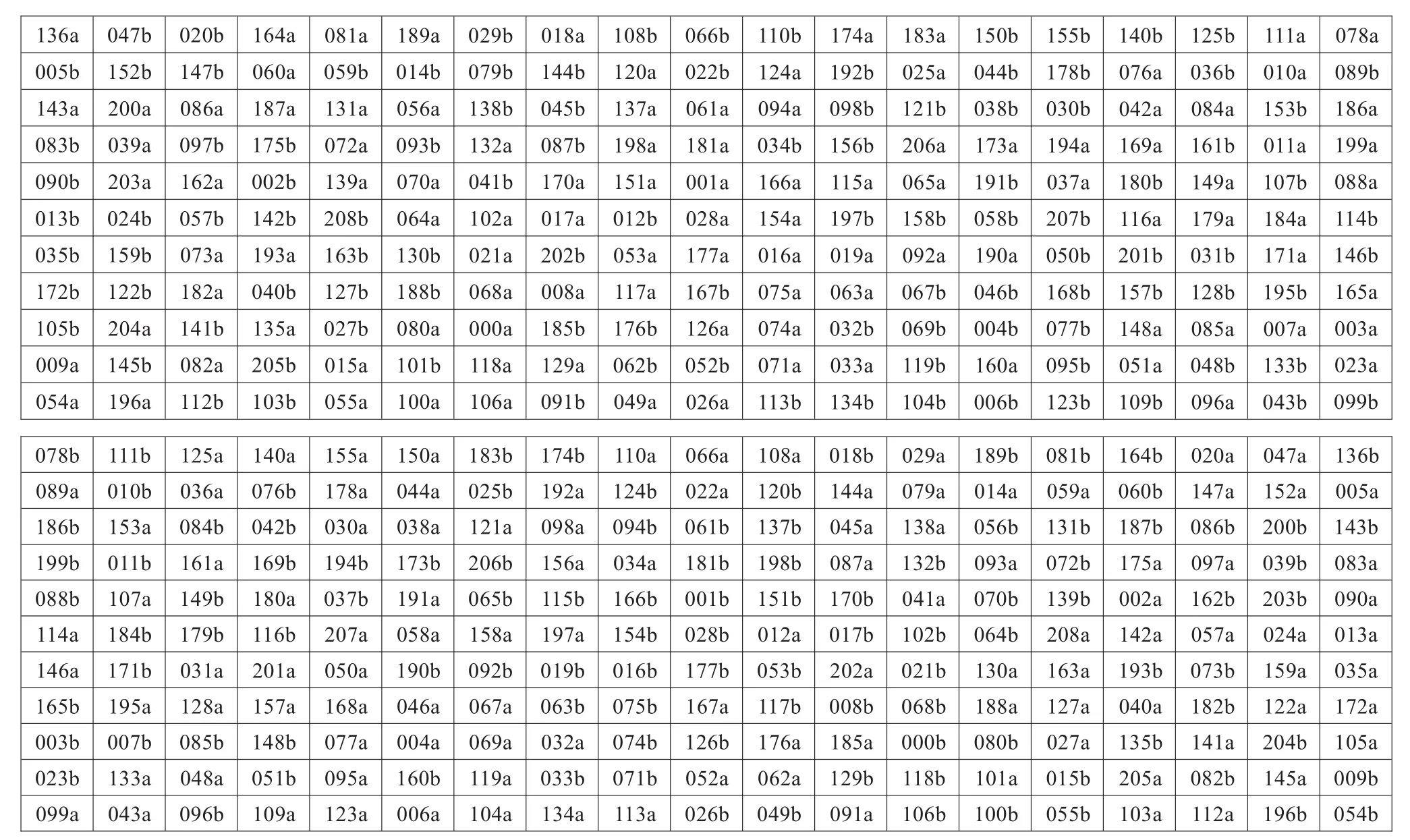
图6 复原后横纵向均进行碎纸的双面碎纸块拼接序号表

图7 横纵向均进行碎纸的双面碎纸块拼贴前后对比图
7 结束语
本文针对碎纸机撕碎纸片的三种形式,提出了基于动态聚类的文档碎纸片自动拼接算法,即分别对仅纵向碎纸条、横纵向均进行碎纸的单面碎纸块和横纵向均进行碎纸的双面碎纸块,进行自动拼接和复原。为了初步解决碎纸片的行聚类问题本文提出了基于碎纸片特征向量的动态聚类方法;为了提高拼接的效率和复原的成功率,提出以同行碎纸片的特征向量及文字中心线为依据,进行动态聚类的后期处理,确定出最终的行分类以及行间排序,减少了搜索的范围;在确定出最终的行分类以及行间排序后,为了得出每一行碎纸片的行内排列顺序,最后得到整篇文档的拼接结果,提出了四邻近匹配的拼接算法。
对上述三种模式的碎纸片拼接算法验证可以看出,该算法不仅可用于汉字文档的拼接,而且也可用于英文文档的拼接。该算法能快速有效解决矩形碎片拼接问题,人工干预很少,成功几率较大。若匹配时加入文字模式识别算法,将更加完善该算法,这也是今后的努力方向。随着碎纸片拼接技术的成熟,一定会给相关行业带来极大的方便。
[1]贾海燕,朱良家,周宗潭,等.一种碎纸自动拼接中的形状匹配方法[J].计算机仿真,2006,23(11):180-183.
[2]王玉亮,沈建新,廖文和.基于SIFT特征的眼底图像自动拼接[J].中国图象图形学报,2011,16(4):654-659.
[3]Gama Leitao H C,Stolfi J.A method for the reassembly of two-dimensional fragmented objects[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(9):1239-1251.
[4]Kong W,Kimia B B.On solving 2D and 3D puzzles using curve matching[C]//Proceedings of the CVPR,Hawaii,USA,2001:583-590.
[5]Pan Rongjiang,Meng Xiangxu,Tu Changhe.Fragment reassembly based on LCS matching[J].Chinese Journal of Computers,2005,28(3):350-356.
[6]Dabak A G,Schmidl T,Sengupta C.Equalizaiton and multi user detection for Space Time block coding based Transmit Diversity(STTD)in frequency selective channels[C]//IEEE VTS Fall VTC 2000,2000:506-513.
[7]王磊,莫玉龙,戚飞虎.基于Canny理论的边缘提取改善方法[J].中国图象图形学报,1996,3(1):191-195.
[8]何鹏飞,周宗潭,胡德文.基于蚁群优化算法的碎纸拼接[J].计算机工程与科学,2011,33(7):67-73.
[9]罗智中.基于线段扫描的碎纸片边界检测算法研究[J].仪器仪表学报,2011,32(2):289-294.
[10]高剑,张彩明,孟祥旭,等.一种基于DDTW的三维碎片自动拼接方法[J].计算机学报,2009,32(2):342-349.
[11]朱延娟,周来水,刘毅.二维非规则碎片匹配的算法[J].计算机工程,2007,33(24):7-9.
[12]刘金根,吴志鹏,刘上乾,等.一种基于特征区域分割的图像拼接算法[J].西安电子科技大学学报,2002,29(6):768-771.
[13]罗智中.基于文字特征的文档碎纸片半自动拼接[J].计算机工程与应用,2012,48(5):207-210.
[14]姜惠兰,安敏,刘晓津,等.基于动态聚类算法径向基函数网络的配电网线损计算[J].中国电机工程学报,2005,25(10):35-39.
[15]朱红霞,沈炯,李益国.一种新的动态聚类算法及其在热工过程模糊建模中的应用[J].中国电机工程学报,2005,25(7):23-27.

