一种非90°移相器的等波纹逼近设计方法

刘渭清

LIU Weiqing

1.西安文理学院 物理与机械电子工程学院，西安 710065

2.西安电子科技大学 电子工程学院，西安 710065

1.School of Physics and Mechatronics Engineering,Xi’an University of Arts and Science,Xi’an 710065,China

2.School of Electronic Engineering,Xidian University,Xi’an 710065,China

1 引言

理想希尔伯特变换器（Hilbert Transformer）经历了从90°移相器到非90°移相器两个发展阶段。90°移相希尔伯特变换器是一个全通滤波器，它对输入信号产生90°相移；目前，在通讯系统及图像的边缘检测中获得了广泛的应用[1-2]。最近几年，非90°移相希尔伯特变换器（Fractional Hilbert Transformer，FHT）在数字通讯及信号处理中也已有广泛应用[3-5]；文献[6-8]介绍了非90°移相器在微波通讯领域中的应用。文献[9]给出了理想非90°移相希尔伯特变换器的定义：

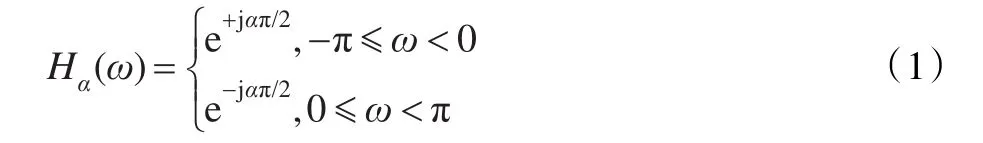
式中尺度因子α是一个指定的参数，且0＜α＜1。可以看出，90°移相器仅仅是非90°移相器在α=1时的特例。理想的90°移相希尔伯特变换器（HT）主要采用具有线性相位的FIR滤波器III型结构近似实现；然而该方法对非90°移相器的设计并不适用，因为它只能产生固定90°移相。文献[10-12]探讨了基于全通滤波器的，以π/2为中心的最大平坦准则意义下的优化设计方法。这些方法的主要特征是其随着频率离π/2越远其误差越大，即误差分布不均匀；而且不能指定通带宽度。文献[13]给出了一种时域设计方法，其特征是滤波器幅度特性不一定为常数。本文提出了一种基于倒谱系数，利用加权最小二乘技术设计具有指定通带宽度且等波纹逼近的非90°移相器，其设计误差在通带呈均匀分布，从而提高了滤波器的频率选择性。

2 基于倒谱系数的非90°移相器设计原理

由理想非90°移相器的定义可知，其相当于一个指定相位特性的全通滤波器，且该全通滤波器的理想相位特性为：

其归一化波形如图1所示(α=0.8)。

图1 理想非90°希尔伯特变换器相位响应(α=0.8)

下面给出一种满足式（2）所示相位特性全通滤波器的设计方法。

2.1 全通滤波器相位响应的特点

一个N阶数字全通滤波器的系统函数为：

可以看出，全通滤波器由其分母多项式系数完全确定，其相位响应可表示为：

这里θN(ω)和θD(ω)分别代表分子和分母多项式的相位响应，因而全通滤波器的相位响应可由阶数N和分母多项式相位确定。

2.2 分母多项式的相位响应与分母系数的复倒谱序列之间的关系

若全通滤波器H(z)是一平稳滤波器，则其分母多项式D(z)必定是具有全极点的最小相位系统[14]；而最小相位系统的复倒谱序列一定是一个因果序列；根据倒谱序列的意义，全通滤波器分母多项式的频率响应D(ω)的对数可表示为：

这里的d(k)代表分母多项式系数所对应的复倒谱序列。另外

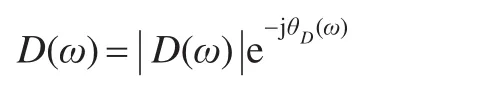
取对数有：

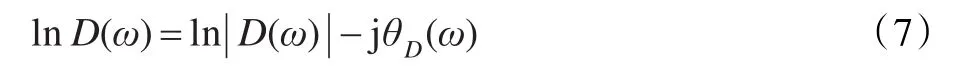
比较式（6）和式（7）有：

其中复倒谱序列d(k)一定是实因果序列。式（8）给出了全通滤波器分母相位响应θD(ω)与分母多项式系数an的复倒谱序列d(k)之间满足的关系。为了由式（8）求出复倒谱序列d(k)，可构造一纯虚奇对称相位函数。对式（8）乘以虚数单位 j，即

由于sinkω是一奇对称函数，d(k)为一实序列，因而式（9）为一纯虚奇对称函数。根据傅里叶变换的对称性质，式（9）的傅里叶逆变换为倒谱序列d(k)的奇对称分量do(k)，

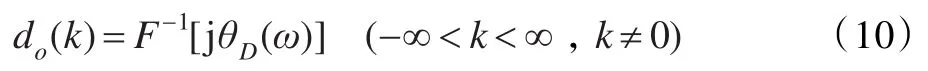
又d(k)是一实因果序列，因而可从其奇对称分量中恢复出d(k)，

定义d(0)=0。根据复倒谱的基本理论，最小相位序列与其复倒谱系数之间满足：

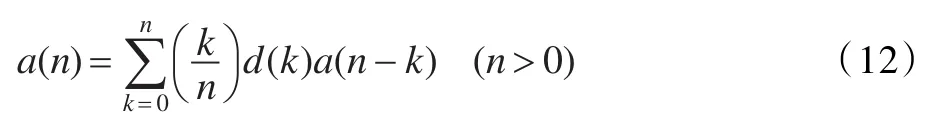
其中a(0)=1，由式（12）可求得分母多项式的系数。上述过程推导出了具有奇对称相位特性的系统的相位与其复倒谱系数之间的关系。据此给出了一种满足奇对称相位要求的全通滤波器的设计方法。

3 非90°移相器的等波纹逼近法设计原理

非90°移相器的设计本质上是具有奇对称相位特性的全通滤波器的设计。因而上述方法即可用来设计非90°移相器。然而一般情况下，系统的倒谱系数为无穷长序列；在滤波器阶数一定的条件下，只能对所求的倒谱值进行截断，因此造成设计结果的低频和高频附近误差较大。其误差的一般化波形如图2所示。另外，考虑到实际应用中并不需要全频带的相位特性，本文提出了一种指定相位频带宽度的、基于倒谱系数的等波纹逼近设计方法，使设计误差在指定频带上呈等波纹分布，从而提高了滤波器的频率选择性。根据式（2）和式（5）可知，分母相位函数为：

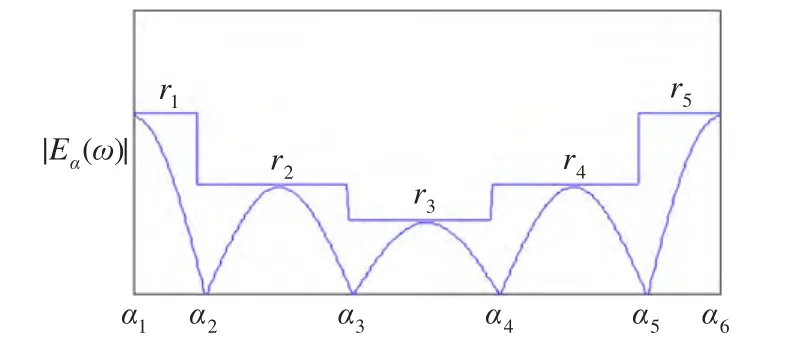
图2 误差函数的一般形式

这里需要说明的是，并不需要考虑式（5）中的线性相移-Nω。因为线性相移可由若干个单位延时来补偿。

3.1 最小二乘等波纹逼近法设计原理

为了实现相位的等波纹逼近，首先采用最小二乘法求得目标相位特性的等波纹逼近函数；然后根据式（10）和式（11）求得其所对应的倒谱序列；最后由式（12）得到设计结果。

（1）加权最小二乘法的基本原理

设 θD(ω)是目标相位函数（分母相位函数），θd(ω)为θD(ω)在指定频带（例如 0.2π～0.8π）上的逼近函数。根据最小二乘法的相关理论，定义误差函数的加权平方和：

其中 Eα(ω)=θD(ω)-θd(ω)是在指定频带上的误差函数，W(ω)为加权函数，K是在误差函数上的采样点数。由式（8）可知，逼近函数 θd(ω)可定义为：

上式中的M称为初始滤波器阶数（不是最终设计的阶数）。式（15）可用矩阵形式表示为 bTs(ω)，其中：

为了使加权平方和Emse最小化，对式（14）求偏导数，

得到线性方程组Ab=d，其中：

这里A是一个实对称的正定矩阵，因此方程有唯一解b。在求解方程组时，为了避免求矩阵的逆矩阵，同时为了提高所求解的精度，可采用柯列斯基分解法（cholesky decomposition）或Hopfield神经网络。求解方程组后可以得到使Emse最小化时的逼近函数θd(ω)。但此时的误差逼近函数并不是等波纹分布的。误差函数的一般形式如图2所示。

（2）加权函数W(ω)的确定

为了实现等波纹逼近，需要确定合适的加权函数。加权函数W(ω)可采用迭代方法求出。设Wk(ω)是第K次迭代的加权函数，那么，第K+1次迭代的加权函数可定义为Wk+1(ω)=Wk(ω)βk(ω)，更新函数βk(ω)可由误差函数的包络轨迹来确定[15]。

由图2可知，|Eα(ω)| 在 [0，π]上的谷底频率处具有局部极小值 αi，i=2，3，…，5。 α1和 α6是边界频率。误差函数在两个连续的αi之间的极大值可表示为：

其中1≤i≤u-1，u-1为谷底频率的个数，α1和 αu+1是滤波器的边界频率。更新函数可以定义为：

更新函数βk(ωl)表示了在每次迭代后，误差函数的分布情况。令 q=[βk(ω1)βk(ω2)…βk(ωN)]T，同时令：

设定ε为一个较小的正数（例如，0.01），如果：

成立，则认为误差函数达到了等波纹分布。否则，按Wk+1(ω)=Wk(ω)βk(ω)调整加权函数，并且对加权函数用其最大值作归一化处理。在首次运算时，可设W0(ωl)=1。另外，为了提高迭代的速度，可按更新权函数，其中θ在1.2至1.7之间（这一点很必要）。

（3）最小二乘等波纹逼近法的计算步骤

①初始化权函数W0(ωl)。

②计算矩阵A和d，并求解线性方程组Ab=d。

③计算误差函数 Eα(ω)。

④确定 αi和 ri；进而求得βk(ωl)和 c。

⑤如果c≤ε（例如0.01），保存向量b，退出；否则，更新权函数，返回第二步。

3.2 求逼近函数所对应的倒谱序列

将上述利用加权最小二乘法经迭代运算确定出的向量b代入式（15），即

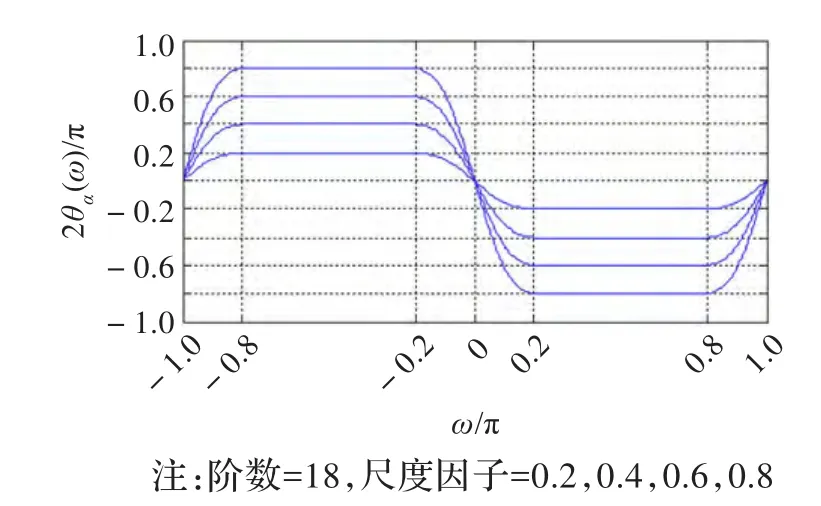
图3 设计滤波器的相位响应

图4 设计滤波器的相位响应

图5 滤波器阶数=18的误差函数

图6 滤波器阶数=36的误差函数

可延拓求得在整个频带上的逼近函数θd(ω)，然后依据式（10）及式（11），即

求得逼近函数θd(ω)所对应的倒谱值d(k)。将d(k)代入式（12）即可求得分母多项式系数an，进而得到所需的非90°移相器的系统函数。需要说明的是以上运算多在离散频域进行；理论上式（16）计算结果应只有前M项为非零值。然而，由于受到频域采样点数的限制，式（16）的计算结果除前M项外仍有非零值，即造成了倒谱值的泄漏。为了达到等波纹逼近的要求，一般应选取d(k)的长度为M的2～3倍。d(k)的长度决定了最终设计滤波器的阶数N。在具体设计时，可根据精度要求确定初始滤波器阶数M。

4 设计举例

为了进一步阐明上述方法的可行性和有效性，本章给出一个设计实例。指标为：尺度因子α分别取为0.2，0.4，0.6，0.8；通带宽度设定为 ωa≤|ω |≤ωb，ωa=0.2π，ωb=0.8π ；在整个设计过程中，全频带 [0，2π]上的采样点数设定为512，根据对称性并考虑到设计在正频率方向进行，故在[0，π]上采样k=256点。

作为比较，本例设计了两款不同阶数的非90°移相器。初始滤波器阶数设定为M1=6和M2=12。首先根据式（15），通过迭代运算得到[0，π]上的256点等波纹逼近函数θd(ω)的样值；根据对称性可得全频带[0，2π]上的512点样值。然后，根据式（16），利用快速傅里叶变换IFFT求得512点的倒谱值d(k)；分别取其前18项和36项（M的3倍）代入式（12），即可得到设计结果。最终的滤波器阶数分别为N1=18和N2=36。图3和图4分别给出了设计结果的相位波形，图中相位幅度用π/2归一化。考虑到篇幅有限，图5和图6仅仅给出了图3和图4中α=0.8时在通带内的误差函数E(ω)的波形。可以看出，在通带内等波纹逼近良好，且随着阶数的增加，其精度显著提高。通过对不同的尺度因子和不同的带宽作类似的设计可知，尺度因子越小，带宽越窄，其设计精度越高。

5 结论

本文提出了一种非90°移相希尔伯特变换器的等波纹逼近设计方法。其核心思想是：在求得分母相位的等波纹逼近函数后，利用逼近函数的奇对称特性构造一个纯虚奇对称的相位函数；然后，利用傅里叶逆变换求得逼近函数的倒谱系数，从而得到所要求的设计结果。由于相位逼近函数的阶数可任意指定，因而理论上，该方法可实现在指定频带上对理想相位的无限精度等波纹逼近。

[1]Kohlmann K.Corner detection in natural images based on the 2-D Hilbert transform[J].Signal Processing，1996，48（3）：225-234.

[2]Kim K J，Kim J H，Jung T H.Closed-form design of sharp fir half-band filters，Hilbert transformer，and differentiator[C]//New Circuits and Systems Conference（NEWCAS），2011 9th International，Bordeaux，2011：181-184.

[3]Zayed A I.Hilbert transform associated with the fractional fourier transform[J].IEEE Signal Processing Letters，1998，5（8）：206-208.

[4]Pei S C，Yeh M H.Discrete fractional Hilbert transform[J].IEEE Trans on Circuits and Systems II：Analog and Digital Signal Processing，2000，47（11）：1307-1311.

[5]Tseng C C，Pei S C.Design and application of discretetime fractional Hilbert transformer[J].IEEE Trans on Circuits and Systems II：Analog and Digital Signal Processing，2000，47（12）：1529-1533.

[6]Han Y，Li Z.Photonic-assisted tunable microwave pulse fractional hilbert transformer based on a temporal pulse shaping system[J].IEEE Photonics Technology Letters，2011，23（9）：570-572.

[7]Li Z.A continuously tunable microwave fractional hilbert transformer based on photonic microwave delay-line filter using a polarization modular[J].IEEE Photonics Technology Letters，2011，23（22）：1694-1696.

[8]Li Z，Han Y.A continuously tunable microwave fractional hilbert transformer based on a nonuniformly spaced photonic microwave delay-line filter[J].Journal of Lightwave Technology，2012，30（12）：1948-1953.

[9]Lohmann A W，Mendlovic D，Zalevsky Z.Fractional hilbert transform[J].Optics Letters，1996，21（4）：281-283.

[10]Pei S C，Wang P H.Maximally flat allpass fractional hilbert transformer[C]//IEEE International Symposium on Circuits and Systems（ISCAS’2002），2002：701-704.

[11]Fernandez-Vazquez A，Jovanovic-Dolecek G.Design of digital fractional Hilbert transformers using allpass filters[C]//Intelligent Signal Processing and Communication Systems，2005：525-528.

[12]Pei S C，Lin H S，Wang P H.Design of allpass fractional delay filter and fractional hilbert transformer using closedform of cepstral coefficients[C]//Circuits and System，2007：3443-3446.

[13]Pei S C，Wang P H，Lin C H.Design of discrete fractional hilbert transformer in time domain[C]//Circuits and Systems，2008：2661-2664.

[14]Rajamanni K，Yhean-Sen L.A novel method for designing allpass digital filters[J].IEEE Signal Processing Letters，1999，6（8）：207-209.

[15]Sunder S，Ramachandran V.Design of equiripple nonrecursive digital different ors and Hilbert transforms using a weighted least-squares technique[J].IEEE Transactions on Signal Processing，1994，42（9）：2504-2509.