小波与自蛇模型在放大图像清晰化中的应用
雷建坤 钟铭华 张凯歌 王鑫 蒋慕蓉
Lei Jiankun,Zhong Minghua,Zhang Kaige,Wang Xin,Jiang Murong1
云南大学 信息学院计算机科学与工程系 昆明 650091
School of Information Science and Engineering,Yunnan University,Kunming 650091,China
1 引言
图像在传输与使用的过程中极易受到外界的干扰,对图像进行放大后,将无法保持原有的视觉效果和清晰度。所以提高放大图像的清晰度是目前迫切需要解决的问题。图像清晰化方法大致可以分为两类:第一类是通过对原图像进行内插值的方法来提高放大图像的清晰度;另一类是对放大后的图像做进一步的优化处理,如增强图像的边缘和细节。第一类方法主要是指经典的线性插值方法和相关的改进插值算法,R.G.Keys[1]通过对平滑内插值放大图像进行分析,针对其高频信息丢失严重的问题,提出基于三次样条的不均匀插值图像放大方法,有效地改善对图像高频信息的处理; Chang[2]等人针对放大图像后在图像边缘出现的块状边缘结构问题,运用近似矢量化逼近的方法对图像进行插值放大,有效地改进了 S.Battiato[3]等人提出的边缘像素自适应图像放大方法。第二类方法主要是指小波插值、分形插值与偏微分方程插值方法。A.Belahmidi和 F.Guichard[4]提出了一种非线性偏微分方程模型,朱长青等[5]先将待放大的图像用内插值方法放大,之后进行小波分解,取其高频系数与原图像一起作小波逆变换得到超分辨图像。袁建军和朱宁[6]对插值放大后的图像,提出了一种基于偏微分方程和三次样条的后处理技术。这些方法都取得了一定效果,但是偏微分模型在计算过程中不可避免地受到迭代次数过多的,使得处理时间过长,容易造成输出图像出现不同程度的模糊和边界震荡效应。
为此,利用小波具有多分辨率分析和局部化时频域特性,引入小波变换对图像进行放大,在一定程度上缓解了传统插值引起的边缘锯齿化和模糊化效应。鉴于小波放大方法普遍存在灰度变暗和边缘模糊问题[7],给出改进的自蛇模型对放大后的图像进行清晰处理。实验结果显示,该算法可以有效地对放大后的图像进行清晰化处理,同时通过对边缘停止函数的修改可以提高算法的时间性能,增强了图像的视觉效果。
2 小波插值
经过小波变换后的图像,可得到良好的空间-频率多分辨率表示,不但能保持原图像的空间特性,还能更好地提取图像的高频信息。同时由于高频分量具有丰富的细节边缘信息,所以可以通过对插值放大后的图像进行小波分解以提取更精确的边缘信息。传统基于小波变换的图像的放大算法都不可避免的存在灰度变暗和边缘模糊问题,本文将传统的内插值算法嵌入到小波变换过程中,得到小波插值(wavelet-interpolation)算法。
算法的具体步骤如下:
Step1:对原始低分辨率图像P进行一级小波分解,结果为[A, H, V, D ]=DWT(P),其中A是小波分解的低频成分,H是水平高频成分,V是垂直高频成分,D是对角线方向的高频成分。
Step2:将分解后的低频分量A采用内插值算法进行放大得到A0。
Step3:图像P直接采用内插值法进行放大,并对放大后的图像进行小波分解得到 AA, H H, V V, DD。
Step4:将第二步中得到的放大后的低频分量A0与第三步得到的水平、垂直、对角线上的高频细节HH, V V, DD进行小波逆变换重构得到放大后的图像PT,即 PT=DWT-1(A0, H H,V V, D D)。
小波插值(wavelet-interpolation)算法流程如图1所示:
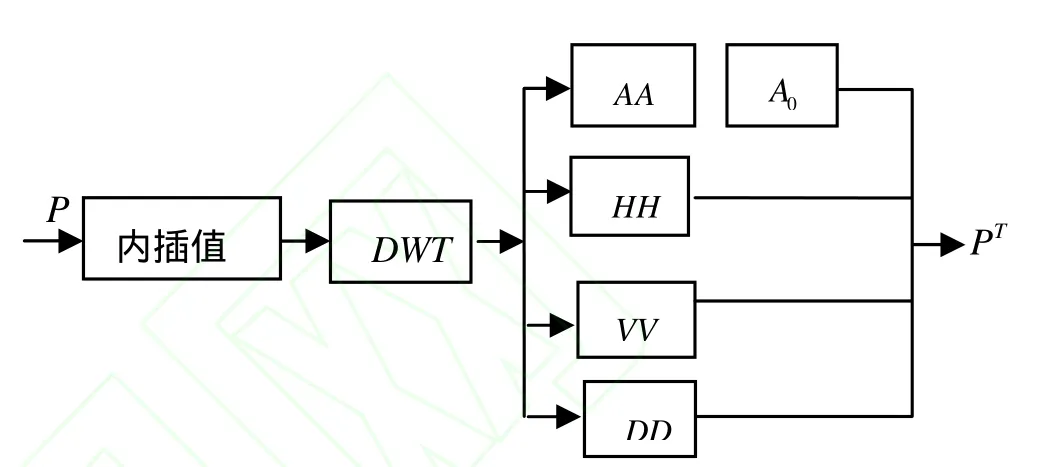
图1 小波插值(wavelet-interpolation)放大算法流程图
3 自蛇模型的改进与计算格式
自蛇模型(self-snake)[8]属于非线性偏微分方程,其表达式如(1)所示:
其中g(ΔI)是边缘停止函数,表达式为公式(2)所示:

其中门限梯度k是选定的常数,一般取 15、16[9],用来控制g的下降速度。本文采用的边缘停止函数为:

比较公式(2)和(3)两个边缘函数,可以看出:
a、新的边缘停止函数(3)取消了门限梯度,使得模型更加的简单化。
b、由于通常梯度门限门限k>1,因此

由(4)式可以知道,边缘停止函数(3)减少了对参数k的讨论,更多的依赖放大后图像的边缘信息,这样就使得在对图像进行后处理时能够对边缘进行较为细致地处理,得到更好的边缘效果。
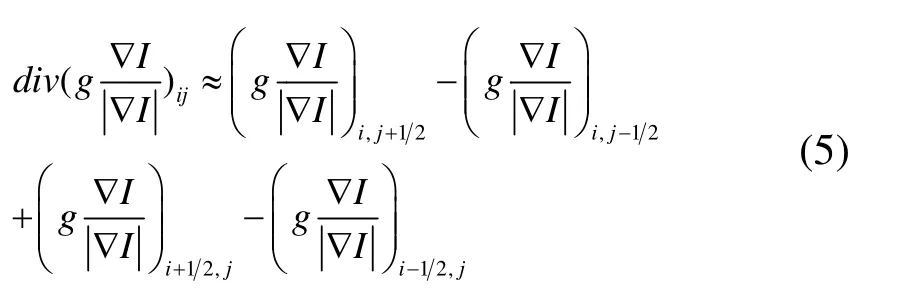
采用“整点”近似来表达(6)式中的每一项,例如,第一项可表示为:

其中梯度的两个分量可表示为:
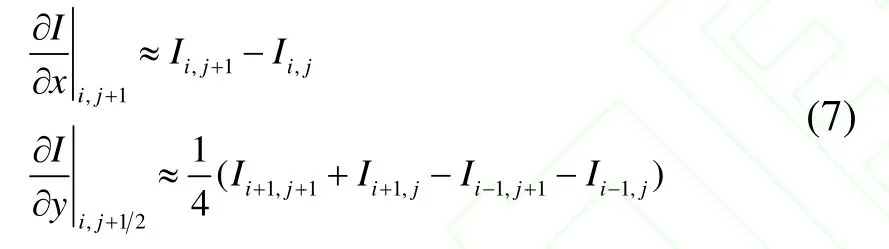
如此,我们就可以用g和I的“整点”值计算(8)式中的第一项。同理,处理其它三项,则散度算子的离散化就完成了。对自蛇模型求粘滞解,其显式计算格式为:

其中:

4 实验结果与分析
实验中用大小为60×60的图像进行放大清晰化处理,为了能够更清楚地观察小波插值的实验结果,采用双性插值得到的图像2(b)做为对比。图2(a)是原始图像,图2(b)是双线性插值放大后的图像,图像整体比较平滑且出现边缘模糊和锯齿化效应,图2(c)对应于小波插值对图像进行放大3倍后的结果图,从图中可以看出,小波插值放大后的图像失真度比较小,目标边缘消除了一部分边缘方块效应,同时图像的灰度变暗。图2(d)是采用本文方法对图像放大3倍的实验效果图,从处理效果来看,本文方法有效地避免了小波插值带来的图像灰度变暗问题而且放大后的图像保持较为清晰的轮廓。

图2 小波插值与改进自蛇模型用于无噪声图像
为量化图像的放大效果,采用峰值信噪比(PNSR)和均方误差(RMSE)来评价图像放大清晰效果的好坏.峰值信噪比是一种比较接近人眼的视觉效果评价量。均方误差用来测量放大图像与标准图像的相近程度。表 1给出了不同算法的峰值信噪比对比结果,由表中结果可以看出,采用小波插值与改进自蛇模型对无噪声图像进行放大清晰处理后,图像的峰值信噪比更高,均方误差值更小。

表1 实验结果图像的PSNR、RSME比较
针对噪声图像在放大的同时也放大了噪声,所以先采用自蛇模型对噪声图像进行去噪和清晰化处理,随后采用小波插值进行放大,实验中选取视频图像《罗马假日》中的一帧噪声图像的局部进行放大清晰化处理,图3为选取原视频中的一帧图像的局部(30×30),实现放大倍数为4。图4(b)为直接对噪声图像进行双线性插值得到的图像效果,从图中可以看出这种插值方法放大了噪声,而图4(c)则采用改进自蛇模型对帧图像的局部进行去噪和清晰处理,随后进行小波插值放大,最终效果如图4(d) 所示,图像的视觉效果较好,符合视频图像清晰度要求。

图3 《罗马假日》中的一帧图像


图4 小波插值与改进自蛇模型用于含噪视频图像
5 结论
本文提出了一种基于小波变换与改进自蛇模型相结合的方法,该方法适用于对无噪图像和噪声图像进行放大和清晰化处理:针对无噪声图像采用小波变换的方法代替传统的插值方法[10],加上对放大后的图像采用改进的自蛇模型进行边缘修正处理,不仅能够避免小波插值放大造成的灰度变暗和边缘模糊问题,而且提高了算法的时间性能,同时由于噪声图像的特殊性,采用自蛇模型对待放大的图像进行去噪和清晰化处理,随后采用小波插值放大处理后的图像。实验结果表明:采用本文方法处理的图像,不仅可以使得图像平滑清晰,而且保持了图像边缘轮廓的细节特征,视觉效果较好。
[1]R.G Keys.Cubic convolution interpolation for digital image processing.IEEE Trans,Acoust,,Sp eech,,Signal Processing,1981,29(6)6:1153–1160.
[2]Chin-Chen Chang,Yung-Chen Chou,Yuan-Hui Yu and Kai-Jung Shih.An image zooming technique based on vector quantization approximation[J].Image an d Vision Computer,2005,23(13):1214-1225.
[3]S.Battiato,G.Gallo,F.Stanco.A locally adaptive zooming algorithm for digital images[J].Image and Vision Computing,2002,20(11):805-812.
[4]Abdelmonnitn Belahmidi,F.Guichard.A Partial Differential Equation Approach to Image Zoom[C].2004 International Conference on Image Processing(ICIP),2004:649-652.
[5]朱长青,王倩,陈虹.基于多进制小波变换的图像放大方法[J].中国图像图形学报,2002,7(3),261-266.
[6]朱宁,吴静,王忠谦图像放大的偏微分方程方法[J].计算机辅助设计与图形学学报,2005 17(9):1 941-1945.
[7]郝鹏威,朱重光.基于小波的图像插值方法[J].遥感学报,1998,2(2):98-102.
[8]吴良武,欧宗瑛.保持轮廓清晰光滑的灰度图像放大算法.计算机辅助设计与图形学学报.2002,1 4(4):306—309.
[9]Osher S,Rudin LI.Feature oriented image en hacement using shock filters.SIAM.J.Num.An aL,1990,(27) ,919—940.
[10]Carey WK,Chuang DB,Hemami SS.Regularity preserving image interpolation.IEEE Trans I mage Proc,1999,8(9):1293-1297.

