特殊旋转二次曲面的性质

周　明

(亳州师范高等专科学校 数学系，安徽 亳州 236800)

圆柱、圆锥、旋转椭球面、旋转双曲线、旋转抛物面都是特殊旋转二次曲面。旋转二次曲面是空间一条曲线(绕着定直线L旋转一周所生成的曲面。[1](P152)通过对特殊旋转二次曲面性质的研究，可以更好建立空间曲面与平面曲线之间的关系。

1　圆柱面

命题1到定直线的距离等于定长的点的轨迹是圆柱面。

证明以定直线为z轴，建立直角坐标系，定长为r，动点为p(X,Y,Z),

所以有

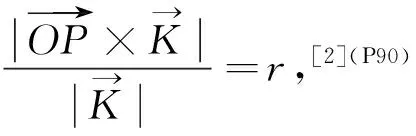
即x2+y2=r2。

所以，点的轨迹是圆柱面。

依题意

2　圆锥面

命题2与定直线相交，且成定角的射线所构成的曲面是圆锥面。

证明设以定直线为z轴，建立直角坐标系，定角为α，定点为坐标原点O(0,0,0),动点为P(x,y,z),

所以

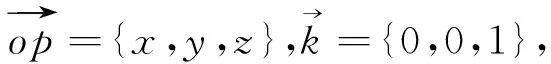
依题义可知

即z2=(x2+y2)cot2α。

所以，射线所构成的曲面是圆锥面。

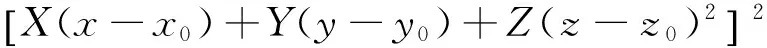
证明设M(x,y,z)是圆锥面上任一点，

所以

所以

(X2+Y2+Z)[(x-x0)2+(y-y0)2+(z-z0)2]cos2α

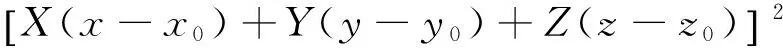
3　旋转椭球面

命题3到两定点的距离之和等于定长的点的轨迹是旋转椭球面。[4]

依题意

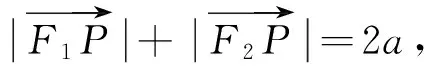
(1)

两边同乘

化简得

(2)

(1)+(2)得

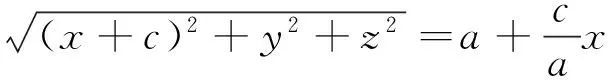
整理可得

(3)

令

所以，点的轨迹是旋转椭球面。

证明设动点为P(x,y,z),

依题意可知

化简得

(a2-c2)x2+a2y2+a2z2=a2(a2-c2),

令

所以，点轨迹是旋转椭球面。

由此可得，到一个定点的距离和到一定平面的距离的比是常数e(e<1)的点的轨迹是旋转椭球面。

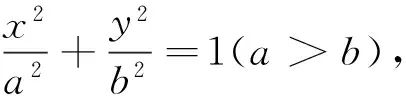
4　旋转双叶双曲面

命题5到两定点距离之差等于定长的点的轨迹是旋转双叶双曲面。[4]

证明以两定点F1,F2,所在直线为x轴，线段F1F2的中点为坐标原点，建立直角坐标系。

依题意

整理可得

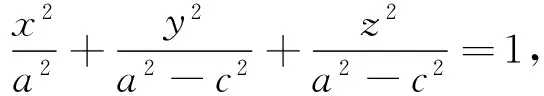
令

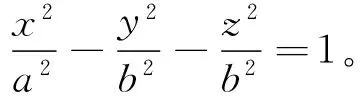
所以，点的轨迹是旋转双叶双曲面。

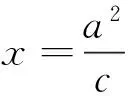
证明与命题4相同。

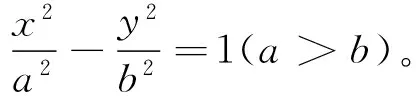
5　旋转抛物面

命题7到定点与到不过此点的定平面的距离相等的点的轨迹是旋转抛物面。[5](P127)

证明取经过定点F且垂直于定平面π的直线为x轴，x轴与π相交于点k,以线段KF的中点为坐标原点，建立直角坐标系。

再设动点为M(x,y,z),

依题意

整理可得

y2+z2=2px。

所以，点的轨迹是旋转抛物面。

由旋转抛物面方程，当转化为平面上时，令z=0，则可直接得抛物线方程y2=2px(p>0)。由此可见，旋转抛物面方程是由抛物线绕其对称轴旋转形成的曲面。

命题8到一个定点的距离和到一定平面的距离的比是常数e的点的轨迹，

当0

当e>1时是旋转双叶双曲面；

当e=1时是旋转抛物面。

此命题与平面曲面椭圆，双曲线，抛物线的性质具有一致性，通过对特殊旋转二次曲面性质的研究，有助于理解二次曲面与二次曲线的关系，更好地理解二次曲面的形成过程。

参考文献：

[1] 吕林根，许子道.解析几何[M].北京：高等教育出版社，2004.

[2] 尤承业.解析几何[M].北京：北京大学出版社,2004.

[3] 纪永强.解析几何[M].北京：高等教育出版社，2013.

[4] 尚云.旋转二次曲面与平面二次曲线的统一[J].济宁师专学报，1998，19(6)：8-9.

[5] 人民教育出版社中学数学室.几何[M].北京：人民教育出版社，1997.