阻力对惯性秤摆动幅度和周期的影响
郑雪梅,黄 瑛,彭 莉,杨建荣
(1.上饶师范学院,江西 上饶 334001;2.上饶县第二中学,江西 上饶 334001)
引言
惯性秤实验对于提高大学生认识惯性质量,学会秤衡质量的一种新方法,具有一定的意义。在现有的大学物理实验教材中,是直接给出惯性秤摆动周期与振动体空载时的等效质量、附加质量块的质量、悬臂振动体的劲度系数三者的关系。要求完成的实验内容有惯性秤的定标、秤衡物体质量和研究重力对周期的影响[1]。其中重力和悬线对摆动周期的影响[2-6]、惯性秤的弹性钢片的等效长度[7]等问题,已有老师进行了分析讨论。而目前使用的惯性秤实验装置,都会出现摆动幅度随时间的增大而明显减小的实验现象,由这一实验现象可知,秤臂和秤台所具有的宽度,在摆动过程中,受到了不可忽略的空气阻力。本文将考虑阻力作用,研究惯性秤摆动的动力学方程,以及阻力对周期和振幅的影响。
1 阻力作用下惯性秤摆动的动力学方程和解
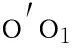
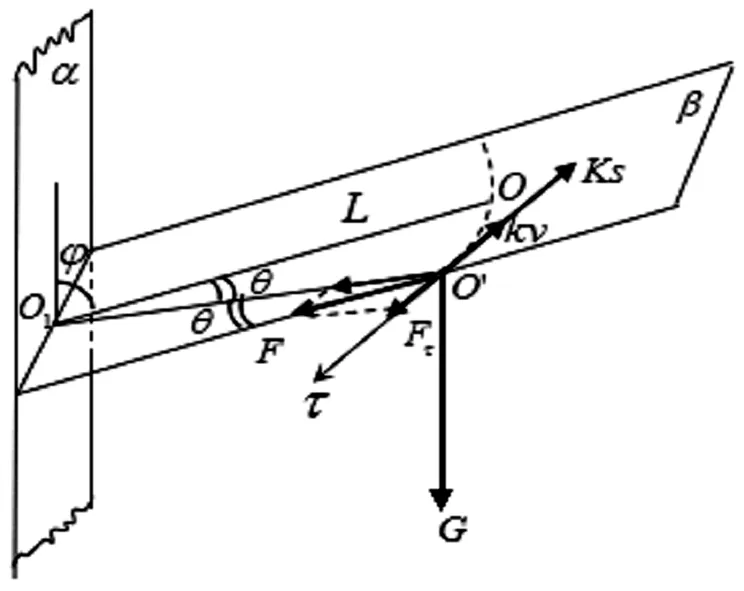
图1 惯性秤实验装置示意图
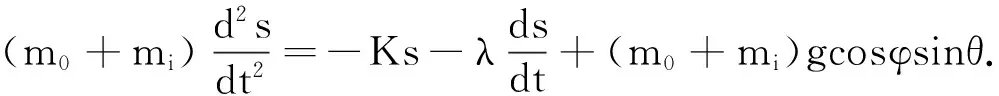
(1)
考虑到s=Lθ,当摆角θ<5°时,可取sinθ≈θ,代入(1)式,得
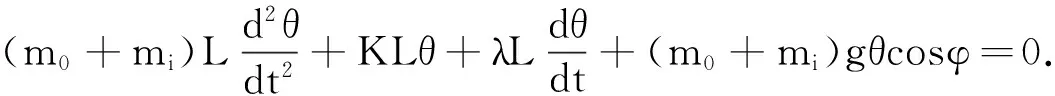
(2)
由此可解得
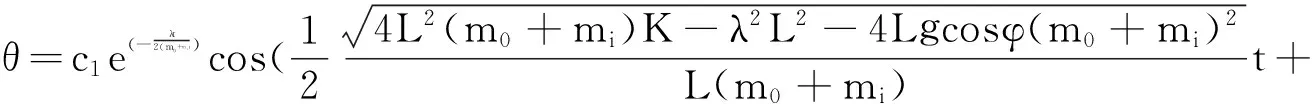
(3)
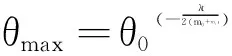
(4)
由(3)式知园频率为
(5)
摆动周期为
(6)
(4)和(6)式分别反映了惯性秤秤台摆动幅度和周期与空气阻力、重力、秤臂等效摆长和质量所存在的关系,下面主要分析讨论其中空气阻力对摆动幅度和周期的影响。
2 空气阻力对摆动幅度和周期的影响
根据(3)式的摆角与空气阻力系数λ、摆体质量(m0+mi)、秤臂的等效摆长L、弹性系数K、夹角φ和摆动时间t等物理量之间的关系,可知,由于空气阻力的存在λ≠0,摆角随时间的增长,摆幅减少,如图2所示。
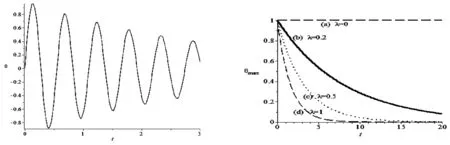
图2 由(3)式决定的摆角与时间的关系,图3 由(4)式决定的摆角θmax与空气空气阻力系数λ=0.5阻力系数和时间的关系
作图时考虑了惯性秤的实际装置,取m0=0.4kg,mi=0.1kg,L=0.4m,K=120N/m,φ=6rad,g=9.8m/s2。由(4)式可进一步知摆角的最大值θmax随时间的增长而呈指数衰减,如图3所示。当空气阻力系数λ=0时,θmax不随时间衰减,是一直线,如图3中的(a)直线;λ≠0,θmax随时间衰减,λ越大,θmax衰减越快,如图3中的(b)、(c)和(d)曲线。另外,由(4)式可知质量(m0+mi)越大,θmax衰减越慢。
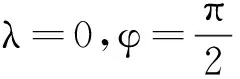
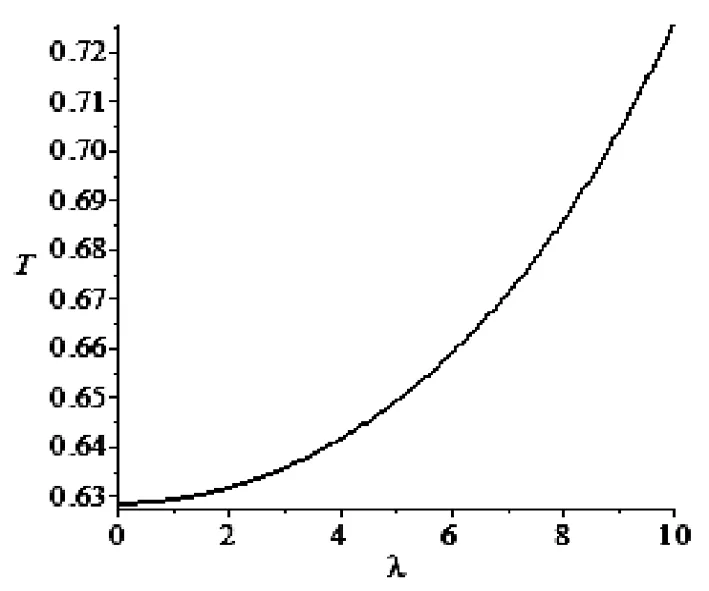
图4 由(6)式决定的空气阻力系数与摆动周期的关系
3 结论
根据惯性秤实验中所出现的摆角随时间增长而衰减的实验现象,推导了具有阻力作用的惯性秤动力学方程,如(1)式。由此而解得摆动幅度随时间增长而逐渐衰减的周期波解,如(3)式。(4)式表明空气阻力系数λ越大,摆动幅度衰减越快,而(6)式表明空气阻力系数λ越大阻摆动周期增大,说明阻力的存在使惯性秤周期增大,忽略阻力的影响,使测量结果比实际待测物的惯性质量要大。另外,文献[1-6]的结果,是本文的一个特例。研究结果对引导学生观察实验现象,养成分析问题的科学态度,培养和提高应用理论解决实际问题的能力,具有一定的意义。如何根据(6)式测量惯性质量和阻力系数,我们将另文讨论。
参考文献:
[1] 杨述武. 普通物理实验: 力学及热学部分[M] . 北京: 高等教育出版社, 2000.
[2] 张秀莲,朱安丽,林长. 惯性秤特性的实验探讨[J].西北师范大学学报(自然科学版),1996,32(2):104-106.
[3] 刘竹琴,刘艳峰,王玉清. 惯性秤振动周期的讨论[J].物理实验,2003,23(7):42-43.
[4] 张淑萍. 重力对惯性秤振动周期影响的分析与实验演示[J].大学物理实验,2010,23(6):53-55.
[5] 曾腾,林红. 惯性秤振动周期的研究[J].海南师范学院学报(自然科学版),2006,19(2):136-139.
[6] 汤云兴,王云霞. 重力对惯性秤影响的实验研究[J].物理实验,2004, 24 (9): 43-46.
[7] 汤云兴. 惯性秤秤台弹性钢片在振动中的作用[J].淮阴师范学院学报(自然科学版),2005,4(2): 120-123.

