层状弹性场地基岩斜入射地震动二维反演
梁建文, 张爱娟, 何 颖
(1.天津大学土木工程系, 天津 300072; 2.天津市土木工程结构及新材料重点实验室, 天津 300072;3.天津大学仁爱学院, 天津 301636)
引 言
基岩地震动求解是进行场地地震响应和结构抗震计算的必要步骤,基岩地震动反演是由场地参数和地表地震记录推求基岩输入运动。20世纪80年代初胡聿贤、谢君斐等就开展了基岩地震动非线性反演的研究[1,2]。陈厚群等通过自由场地表运动的反演分析和正演计算[3],确定坝址河谷自由场地震运动。蔡袁强等采用非线性土层平稳随机地震反应分析的等价线性化方法反演分析了非线性成层地基基岩的地震动[4]。陈清军和刘拓对地震波反演的波动法和有限元法进行了比较[5],并对频率截断问题进行了探讨。
值得指出的是,上述基岩地震动反演均是仅根据地表水平地震动加速度记录来推求基岩面水平地震动,是一维反演问题;而实际上,地表某点的水平加速度记录只是该地表点地震记录的一个方向,在该点同时还有竖向加速度记录和另外一条水平加速度记录,或者说该地表点的实际地面运动是三维的;虽然地震记录通常均是以三个正交方向的地震动来表示,但三个方向的地震动自基岩到地表的传播过程中却是耦合的,或者说,斜入射的波自基岩向地表传播过程中,每遇到一个土层界面均存在波型转换,因此可以设想,仅根据地表水平加速度记录来推求该方向的基岩面水平地震动无疑存在一定的误差。
不失一般性,以二维反演问题为例,本文提出了层状弹性场地基岩斜入射地震动反演的一个方法,方法根据地表一点的水平和竖向的两个加速度记录,进行基岩输入地震动和入射角的反演,并以剪切波斜入射为例对方法进行了验证。最后对文献中一维反演的误差进行了分析。
1 斜入射地震动反演方法
图1所示层状弹性半空间场地,由基岩半空间和其上的N个土层组成。本文的目的是根据地面水平加速度记录uL和竖直加速度记录wL来反演基岩斜入射地震动aSV和斜入射角φ。图中,uR和wR分别表示基岩面运动,uR0和wR0则分别表示基岩露头运动。
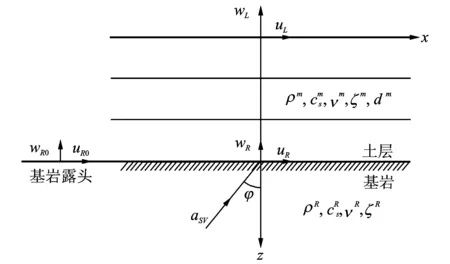
图1 斜入射地震动二维反演模型
利用土层动力刚度矩阵和半空间动力刚度矩阵[6],第m(m=1,2,…,N)个土层和基岩半空间在频域内的动力平衡方程可以分别写为
(1)
(2)
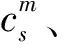
将各土层和半空间的动力刚度矩阵集整,得到场地的动力刚度矩阵K,自由场的动力平衡方程可写为
(3)
上式两边同时左乘K的逆矩阵(柔度矩阵)Δ,得到
(4)
式中 矩阵Δ只与场地动力特性和波入射角度φ有关,右边位移向量中的U1,W1可由地表加速度记录uL和wL的Fourier变换并积分求得。
式(4)展开后得
(5)
方程两边分别相除,并将等号右边项左移,可得如下方程
(6)
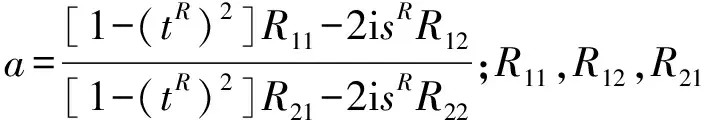
反演的目的在于求解基岩入射地震动和入射角,使得地表加速度时程响应等于地表加速度记录。由于场地动力特性已知,则式(6)为仅含未知量φ的方程,最优求解即可得到基岩入射角φ,进而求得基岩斜入射地震动。
2 斜入射地震动二维反演步骤
以基岩半空间上N个土层场地为例进行反演分析,其主要步骤如下。
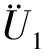
(2)求解方程(6),得出地震波入射角φ。求解的关键在于寻找一个合适的角φ,在所有频率上满足式(6),可采用最小二乘法最优寻解。即考虑M个频率点的残差均方根
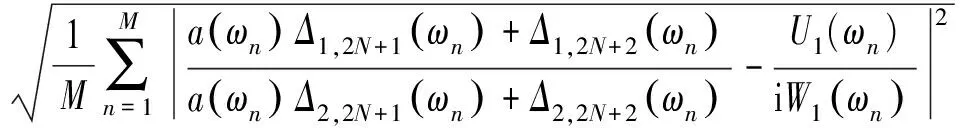
(7)
求取使e取得最小值的角度值φ作为方程的解。值得指出的是,当入射角为0°时方程(6)无意义,自然也无需最优寻解。
(3)将求得的入射角φ代入整体柔度矩阵Δ,求解方程组(5)得到半空间荷载幅值P0和R0。
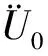
(5)频域内基岩处入射波由下式可得
(8)
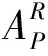
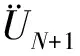
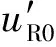
3 方法验证与算例分析
首先,通过模拟产生地表水平和竖向加速度记录。在层状弹性场地(场地土参数资料见表1)基岩处斜入射幅值为0.1g的El Centro波(图2),斜入射角分别为0°,5°,10°,15°,20°,25°,30°,35°和40°,求得地表水平和竖向加速度响应作为地表水平加速度记录和竖向加速度记录,图3给出了斜入射角φ=0°,10°,20°,30°和40°情况下地表水平加速度记录uL和竖向加速度记录wL。
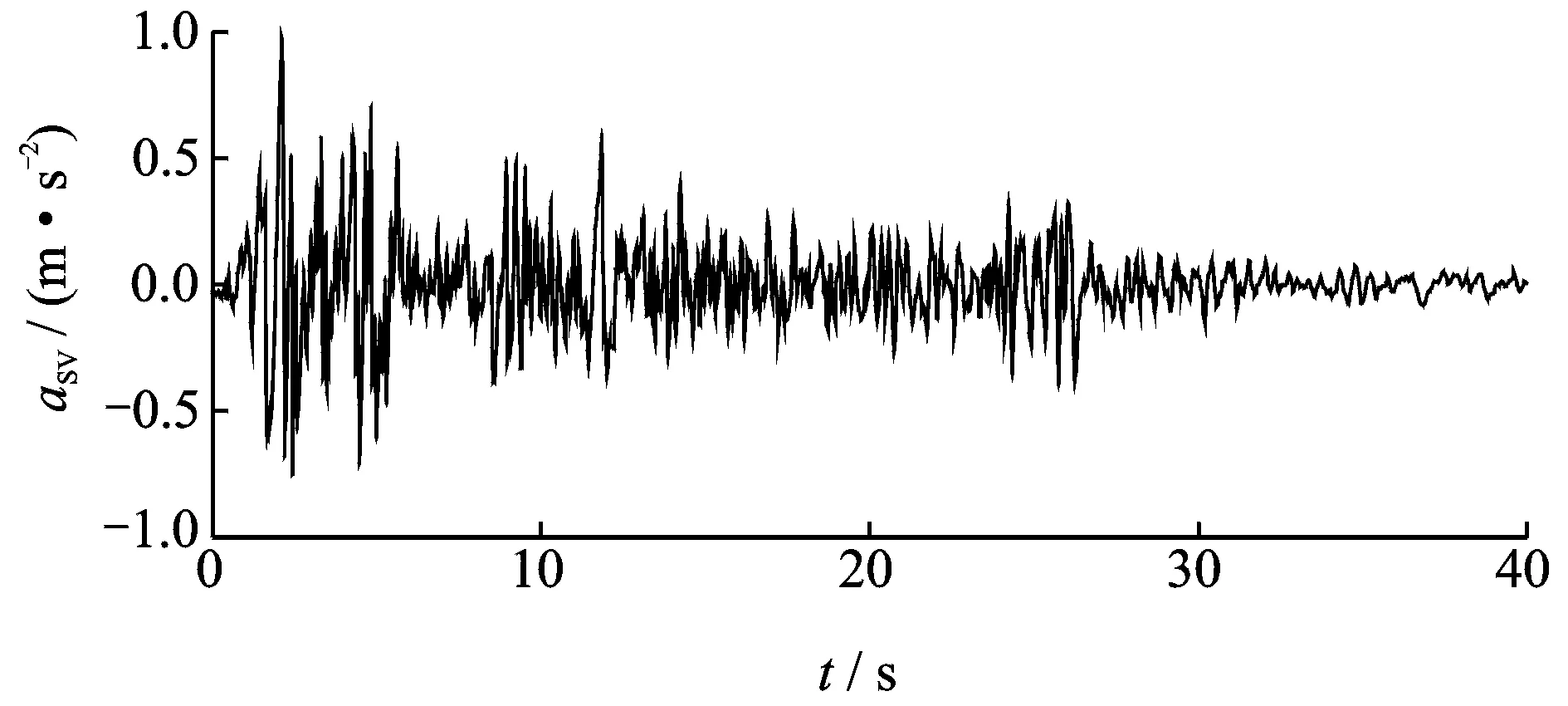
图2 输入地震波加速度时程
3.1 基岩斜入射地震动二维反演
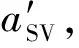
图4给出了基岩斜入射地震动时程二维反演结果和入射角最优寻解结果。值得指出的是,对于入射角为0°的情况,入射角无需最优寻解,仅凭地表无竖向运动即可判断地震波的入射角度(图4(a))。可以看出,在不同(斜入射角情况)地表水平加速度记录和竖向加速度记录情况下(图4(b)),均可以准确反演出基岩斜入射地震动的入射角和时程。说明本文方法是正确的,计算精度是非常高的。
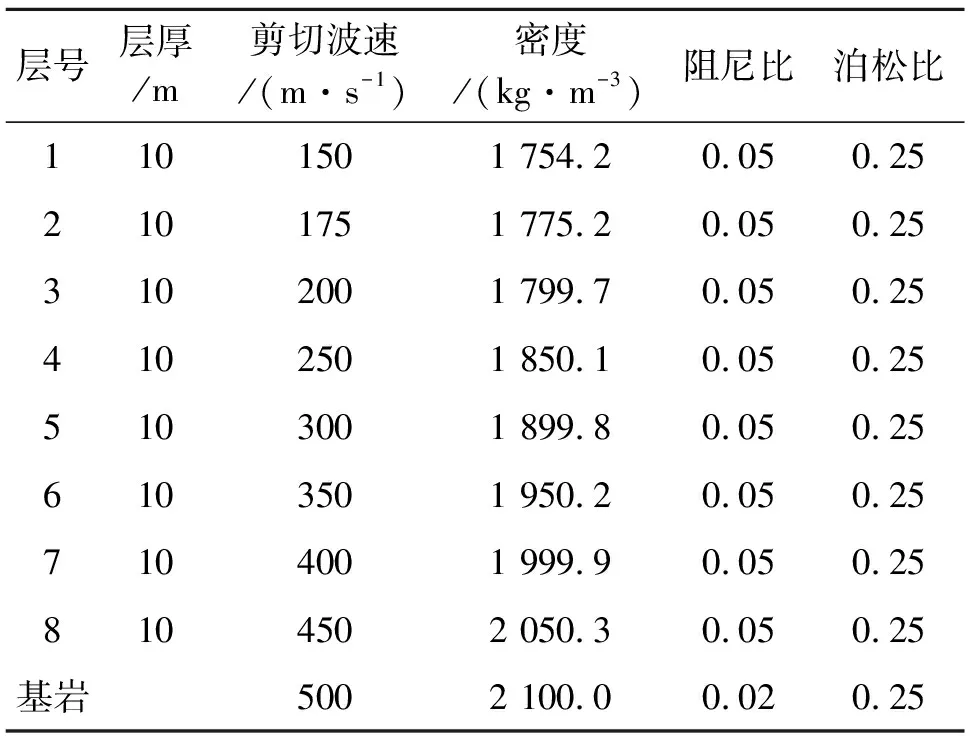
表1 场地基本资料
3.2 基岩垂直入射地震动(一维)反演
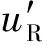
图5给出了入射角为0°,10°,20°,30°和40°情况下,一维反演得到的基岩面运动和基岩露头运动分别与实际基岩面运动和基岩露头运动的比较,表2和3则分别给出了入射角为0°,5°,10°,15°,20°,25°,30°,35°和40°情况下,基岩面运动和基岩露头运动时程的峰值及峰值出现时刻的反演值和实际值的比较。可以看出,斜入射角φ=0°时,反演的基岩面运动和基岩露头运动与实际基岩面运动和基岩露头运动完全重合;随着斜入射角的增大,差别(误差)逐渐增大。可以看出,当入射角φ=25°时,基岩面运动反演误差为9.71%,基岩露头运动反演误差为7.35%,而φ>25°时误差将显著增加。原因在于,虽然地震记录均采用相互正交的地震动来表示,但斜入射地震动自基岩到地表的传播过程中却是耦合的,每遇到一个土层界面均存在波型转换,因此,仅根据地表一条水平加速度记录来推求该方向的基岩面水平运动必然存在一定的误差,且该误差随着实际地震动斜入射角的增大而增大,误差的本质在于忽略了竖向地震动的影响。由于实际地震动无疑是三维的,或者说竖向地震动不可忽视(有时竖向地震加速度峰值甚至大于水平地震加速度峰值),因此,文献中的一维反演可能存在较大的误差,值得重视。
为了进一步说明误差的影响,图6分别给出了入射角为0°,10°,20°,30°和40°情况下,基岩面运动反应谱和基岩露头运动反应谱分别与实际基岩面运动反应谱和基岩露头运动反应谱的比较。可以看出,当入射角φ≥30°时,基岩面运动反应谱和基岩露头运动反应谱均与实际相差已非常明显,此时采用一维反演将造成较大的误差。
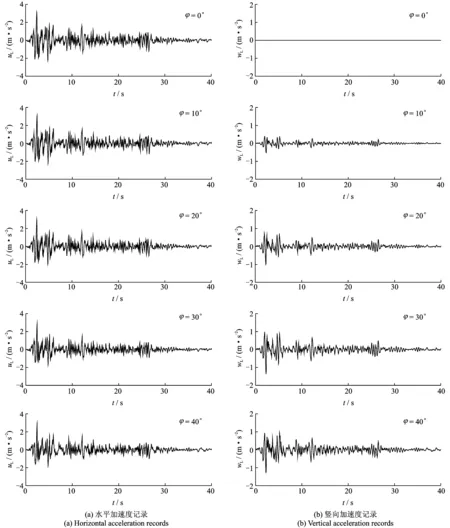
图3 模拟的地表水平和竖向加速度记录
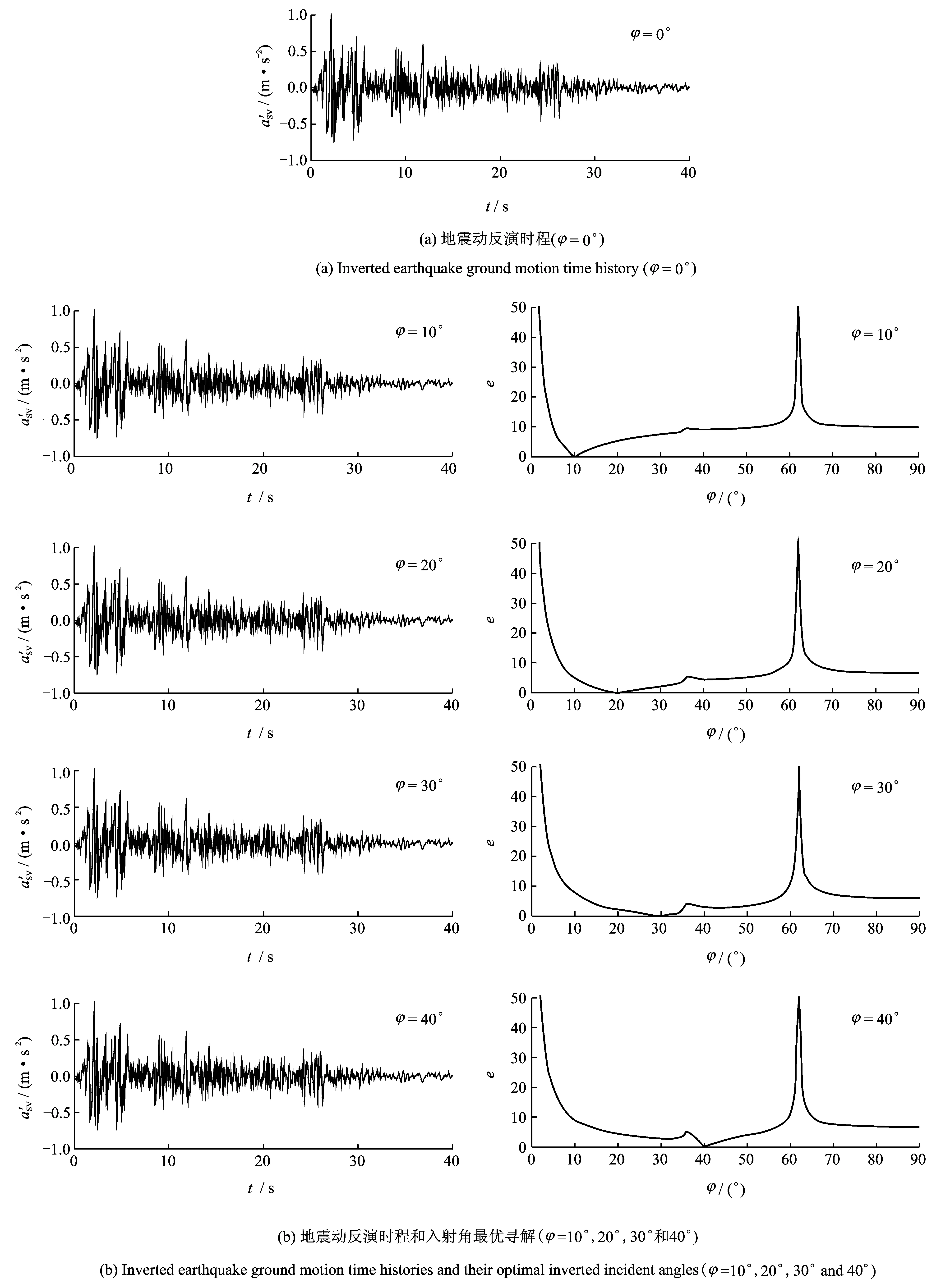
图4 基岩斜入射地震动二维反演结果
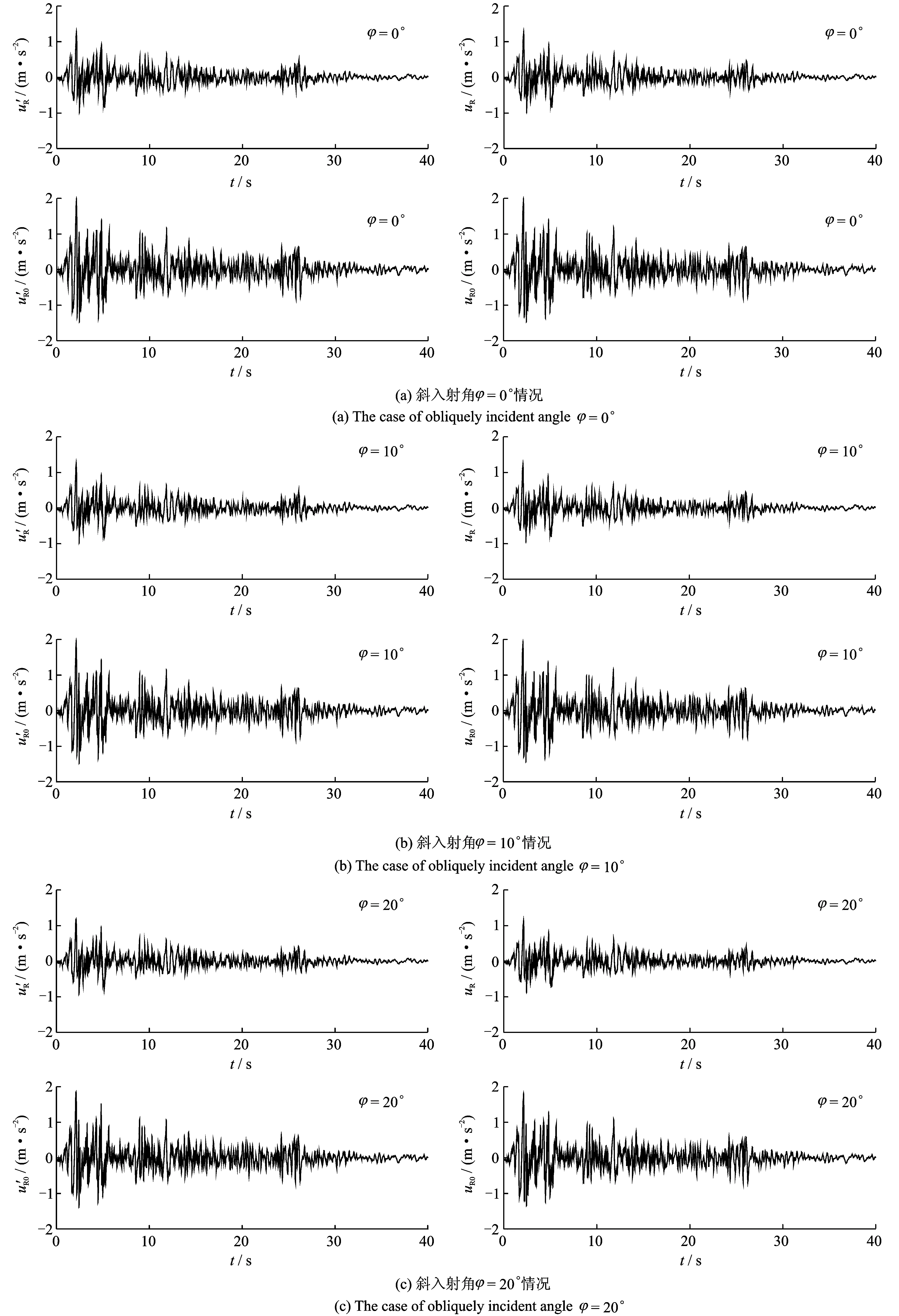
图5 一维反演的基岩面水平运动和基岩露头运动(左图)与实际二维基岩面水平运动uR和基岩露头水平运动uR0(右图)的比较
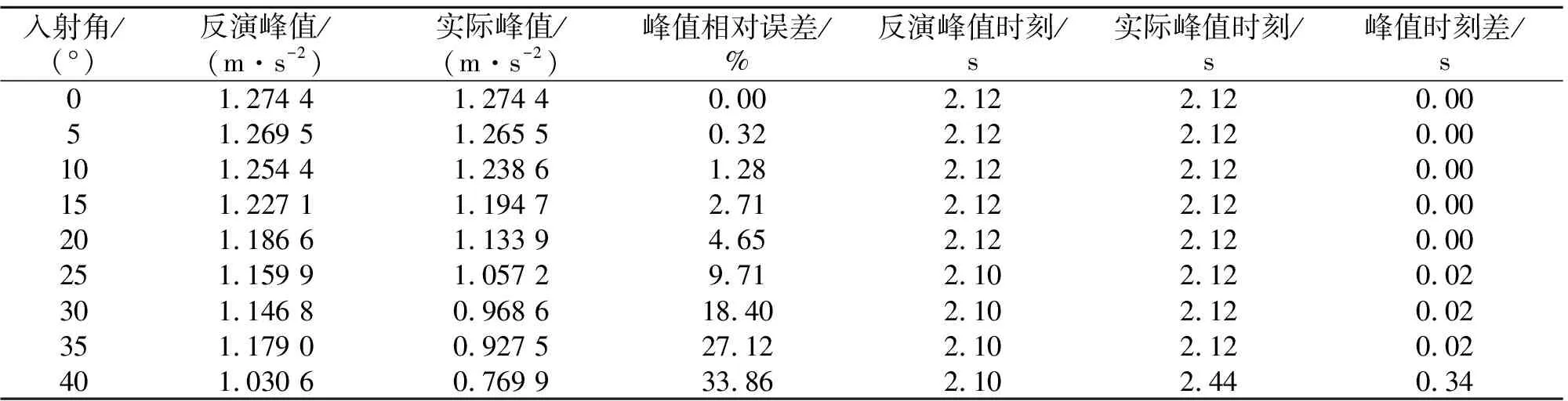
表2 基岩面运动水平加速度时程反演误差
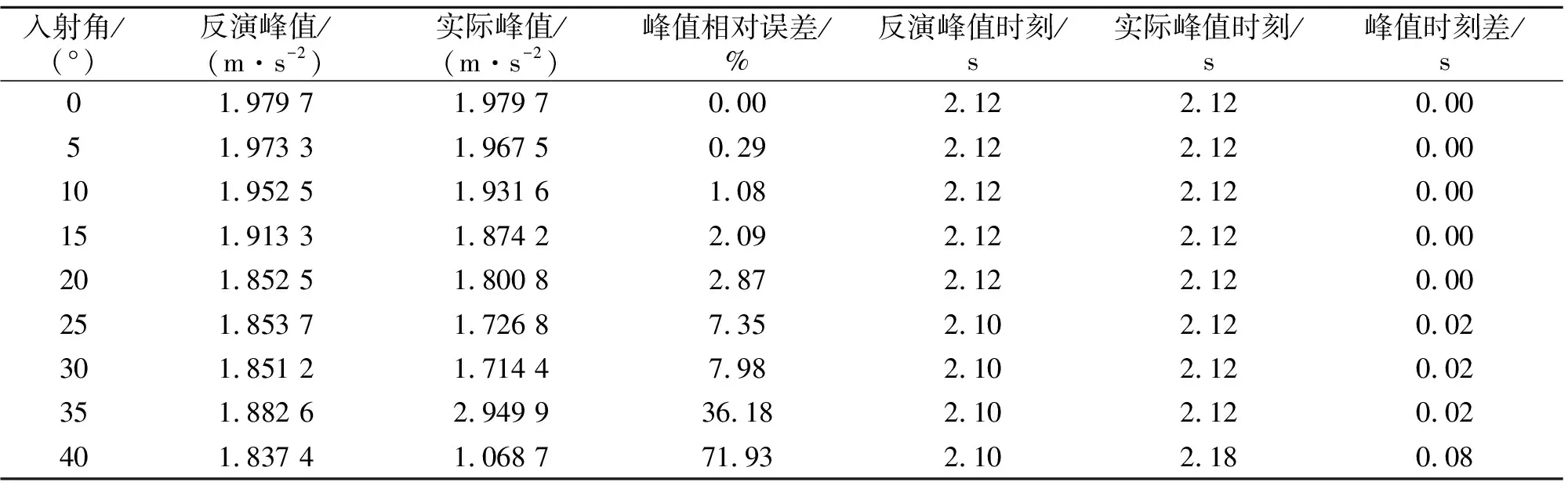
表3 基岩露头运动水平加速度时程反演误差
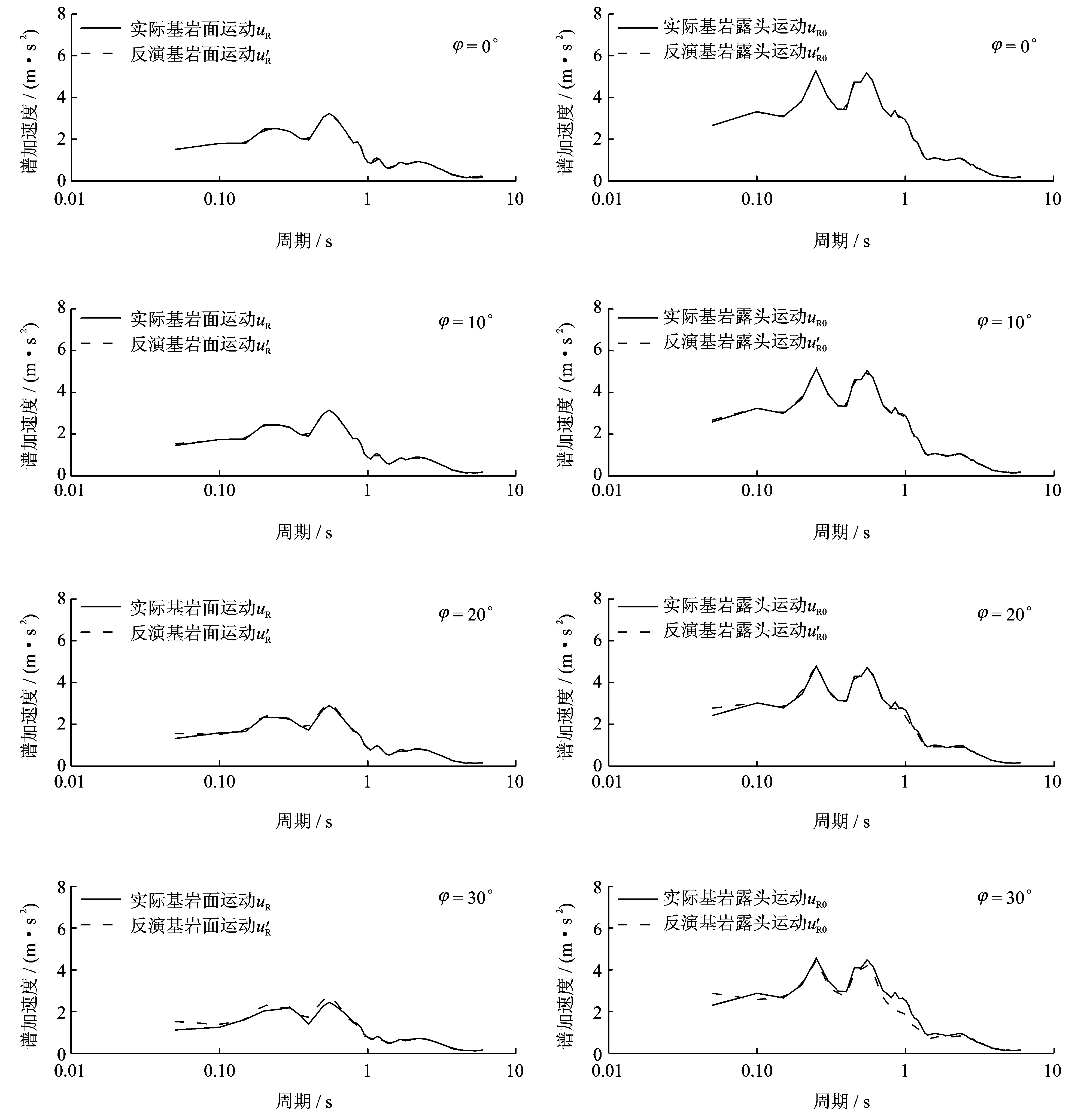
图6 按垂直入射(一维)反演加速度反应谱对比图
4 结 论
本文提出了层状弹性场地基岩斜入射地震动二维反演的一个方法,方法利用半空间和土层的精确动力刚度矩阵,根据地表某一点的水平和竖向的两个地震加速度记录,进行基岩斜入射地震动和入射角的反演,并以SV波斜入射为例对方法进行了验证。研究表明,根据水平和竖向两个地震加速度记录可以准确进行基岩地震加速度时程和入射角的反演。论文并分析指出了文献中一维反演存在的误差及出现误差的原因。
参考文献:
[1] 胡聿贤,朱镜清,朱莉,等.频域中的结构振动输入反演[J].地震工程与工程振动,1981,1(1):41—53.Hu Yuxian, Zhu Jingqing, Zhu Li, et al. Identification of input to vibrational structure in frequency domain[J]. Journal of Earthquake Engineering and Engineering Vibration, 1981,1(1):41—53.
[2] 谢君斐,石兆吉.地面运动的反演及其在震害分析中的应用[J].地震工程与工程振动,1981,1(2):9—24.Xie Junfei, Shi Zhaoji. The inverse calculation of ground motion with application to earthquake damage analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 1981,1(2):9—24.
[3] 陈厚群,侯顺载,王均.拱坝自由场地震输入和反应[J].地震工程与工程振动,1990,10(2):53—64.Chen Houqun, Hou Shunzai, Wang Jun. Earthquake input and free-field motion response of arch dams[J]. Journal of Earthquake Engineering and Engineering Vibration, 1990,10(2):53—64.
[4] 蔡袁强,凌道盛,周迪永,等.非线性分层地基地面运动反演分析[J].振动工程学报,2000,13(3):426—432.Cai Yuanqiang, Ling Daosheng, Zhou Diyong, et al. Inverse calculational analysis of ground motion in non-linear layered soil[J]. Journal of Vibration Engineering, 2000,13(3):426—432.
[5] 陈清军,刘拓.地震波反演两种计算方法比较与频率截断问题的探讨[J].力学季刊,2010,31(3):388—394.Chen Qingjun, Liu Tuo. Comparison of two methods of ground motion inversion and discussion on question of freqnency cut-off[J]. Chinese Quarterly of Mechanics, 2010,31(3):388—394.
[6] Wolf J P. Dynamic Soil-structure Interaction[M]. Englewood Cliffs: Prentice-Hall, 1985.

