输入未知条件下基于自适应广义卡尔曼滤波的结构损伤识别

穆腾飞， 周 丽

(南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016)

引 言

近年来，愈发频繁发生的地震、台风等自然灾害对建筑等土木工程基础设施的安全运行产生了较大的威胁，有能力在线精确地评估结构状态，将有助于突发事件后快速地采取应急措施，合理地规划结构改造的先后次序，减少灾难事故的发生[1,2]。传统的系统辨识理论是建立在系统输入与输出信息均已知的基础上，对时不变参数进行识别，然而，在实际工程应用中，系统输入信息，如地震动、脉动风等是难以精确测量甚至无法测量的；此外，结构参数通常会随着损伤的发生而变化。因此，输入未知条件下系统时变参数追踪技术的研究有着重要的理论价值及广泛的实际工程应用背景[3]。

输入未知条件下系统参数识别领域，诸多方法得到了发展，主要包括频域法和时域法：频域法主要关心系统的模态参数，如随机子空间法、随机减量法和模态函数分解法[4～6]等，此类方法在稳态载荷输入下具有较高的识别精度，但在非平稳载荷输入下具有较大的局限性，此外，该类方法需要重大事件发生前的原始数据作为基准以判断结构损伤[7]；时域法主要关心系统的结构参数，如假定输入为白噪声等平稳随机振动的参数识别、假定结构响应为自由衰减过程的参数识别[8，9]等，此类方法的假设情况通常与实际输入不符，这使得参数估计精度大受影响[10]。以上方法仅能识别系统参数信息，却不能反演对研究具有重要意义的未知输入载荷[11]。近年来，国内外的学者在系统参数与载荷的复合反演方面取得了一定成果，如ILS-UI法、统计平均法、加权平均修正法和动态响应灵敏度分析法[12～15]等；此外，未知风荷载情况下的复合反演也得到了研究[16]。然而，由于整个动力系统非常庞大，需要的是稳定收敛的解析递归解而不是迭代解，这方面仍有待研究。近期，一些经典的系统辨识算法得到了发展，如LSE-UI法，然而该方法仅适用于线性参数系统并不适用于非线性参数系统[17]。为了弥补此点不足及实现对结构时变参数的追踪，Yang等发展了输入未知条件下的自适应广义卡尔曼滤波方法，该方法能够在线复合反演结构参数与未知输入及追踪结构损伤，然而，该方法所应用的自适应技术是通过使用MATLAB中的CONSTR函数求解自适应因子矩阵，在该过程中可能会出现复数，导致损伤追踪失败，这有待进一步改进[18]。一种基于遗传优化算法的自适应追踪技术被提出以弥补以上不足，然而该技术在计算自适应因子矩阵过程中容易陷入局部极值且收敛速度较慢[19]。近期，一种改进粒子群优化(Improved Particle Swarm Optimization, IPSO)算法得到了发展，该算法将传统的粒子群优化技术与佳点集理论及协同进化理论相结合[20～22]，使种群避免陷入局部极值并提高了算法的搜索精度和计算效率，仿真研究表明该方法在解决约束优化问题上的优势[23]。

本项研究发展了输入未知条件下的自适应广义卡尔曼滤波方法，在线复合反演系统参数(阻尼、刚度和非线性参数等)与未知输入(激励)，结合基于改进粒子群优化算法的自适应技术实现系统时变参数的追踪，进而识别结构损伤，包括损伤发生的时间、位置和程度，并以基础隔震结构模型为对象进行振动台实验研究。建立理论模型以模拟基础隔震结构模型的动力学特性，其中，隔震层的非线性动力学特性通过Bouc-Wen模型描述。对其进行振动实验，实验过程中采用刚度元件装置在线模拟结构损伤，测量模型加速度响应，基于测得的加速度响应和AEKF-UI方法在线复合反演结构参数与未知输入，并追踪结构损伤。研究结果表明：在两种典型地震波激励下，通过时间、位置和程度不同的刚度突变模拟结构损伤，AEKF-UI方法得到的结构参数值与分析所获得的参考值相一致，识别得到的未知输入与实验测得的系统输入相吻合，并可以准确地追踪损伤发生的时间、位置和程度，验证了AEKF-UI方法在系统参数与载荷的复合反演及损伤追踪中的有效性和准确性。

1 AEKF-UI算法

在未知输入条件下，m自由度的非线性结构运动方程可表示为

ηf(t)+η*f*(t)

(1)

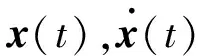
引入广义未知状态向量

(2)

式(1)可以转化为非线性广义状态方程

(3)

式中w(t)为模型噪声，其协方差矩阵为Q(t)。则非线性离散观测矩阵可以表示为

(4)

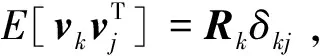
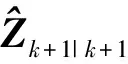
(5)

(6)

(7)

(8)

(9)

(10)

Rk+1]-1

(11)

(12)

(13)

KZ,kHk|k-1)PZ,k|k-1

(14)

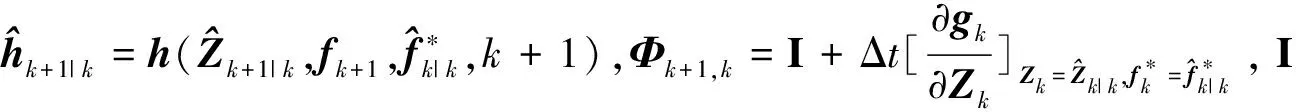
(15)

式中γk+1为m维预测误差向量，Vk+1为γk+1的平方和误差。根据文献[24]中的渐消因子理论可得

(16)

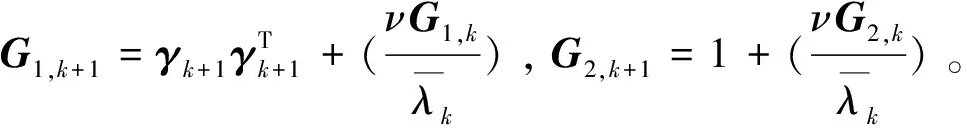
(17)

其中

(18)

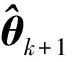
(19)

(20)

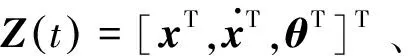
(21)

式中s是采样数，s≤k，本文中采用s=300。以上即为AEKF-UI方法的求解过程。

2 实例分析

2.1 实验装置

实验模型为一个三层剪切型框架(上层结构)安装在GZN110型叠层橡胶隔震支座组(隔震层)上。隔震层尺寸为600 mm×500 mm×315 mm，质量m1=255.5 kg，其参数、性能及相关试验测试结果详见文献[26,27]；上层结构尺寸为400 mm×300 mm×1 035 mm，质量m2=54.5 kg，m3=48.5 kg，m4=24.5 kg。实验中，使用一套可在线改变结构刚度的装置——刚度元件装置(Stiffness Element Device, SED)，以模拟结构在实验振动过程中的损伤[28]。该装置由气缸和支架系统组成，能够为所在结构部位提供一定量的有效刚度。在实验前，先向气缸内充入压缩气体，这时SED就相当于一个空气弹簧；在振动实验过程中，通过排除压缩气体，使SED提供的有效刚度下降为零，以达到在线降低结构部位刚度的目的。实验装置如图1所示。

图1 实验装置图

本项实验将模型固定在ETS GT1200M振动台上，通过UCON VT-9008振动控制器实现地震波基础激励。在基础、隔震层及上层结构上安装PCB 3701G3FA3G加速度传感器，由NI PXI4472B信号采集卡实现信号采集，测量系统的加速度响应，其中基础加速度响应用来和AEKF-UI方法识别得到的未知输入进行比较，判断AEKF-UI方法用于结构未知输入识别的可行性和准确性。实验中所有信号的采样频率均为1 000 Hz。

2.2 基础隔震结构模型

基础隔震结构由隔震层和上层结构组成。本项研究采用广泛应用于非线性建模的Bouc-Wen模型描述隔震层的动力学特性[27,29,30]。基础隔震结构的运动方程可写为

(22)

其中

RT(x1,z,t)=αk1x1+(1-α)k1z

(23)

(24)

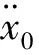
2.3 实验研究

本项研究基于测量得到的加速度信号和简化迟滞模型，通过基于改进粒子群优化技术的AEFK-UI方法实现基础隔震结构模型的在线系统参数与未知输入的复合反演，追踪结构损伤，包括损伤发生的时间、位置和程度。实验前，测量得到实验模型的频率，其前四阶固有频率分别为1.650,2.356,6.941和10.024 Hz，将其视为四自由度剪切梁模型，根据有限元法可得到模型由下至上四层刚度分别为50.9,45.9,46.1和55.4 kN/m[26～28]。这组有限元分析结果在本项研究中将作为参考值，与AEKF-UI法的识别结果作比较，评价该方法的有效性和准确性。在振动实验过程中，分别考虑两种典型实验工况对本文所发展方法进行实验验证，实验研究结果如下。

2.3.1 工况一

基础隔震结构模型受El Centro地震波激励(滤波后频带[1.5～5]Hz，能量分布均匀)，第二层的SED中充入0.75 MPa空气，其提供的有效刚度约为7.5 kN/m，则第二层刚度变为53.4 kN/m，第三层的SED中充入0.45 MPa空气，其提供的有效刚度约为4.5 kN/m，则第三层刚度变为50.6 kN/m。在实验过程中，结构振动到t=15 s时，同时排出第二层和第三层SED中的压缩空气，模拟上层结构刚度突变，则第二层的刚度从53.4 kN/m降低到45.9 kN/m，第三层的刚度从50.6 kN/m降低到46.1kN/m，其他层刚度保持不变。在El Centro地震波激励下，测得的每层的绝对加速度响应ai如图2所示。

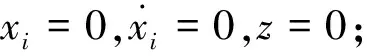
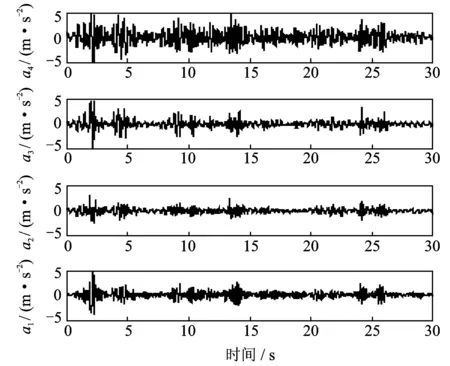
图2 测得的加速度响应(工况一)

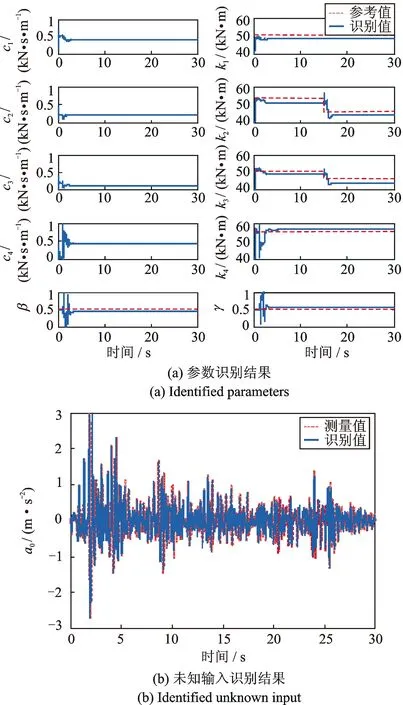
图3 实验识别结果(工况一)

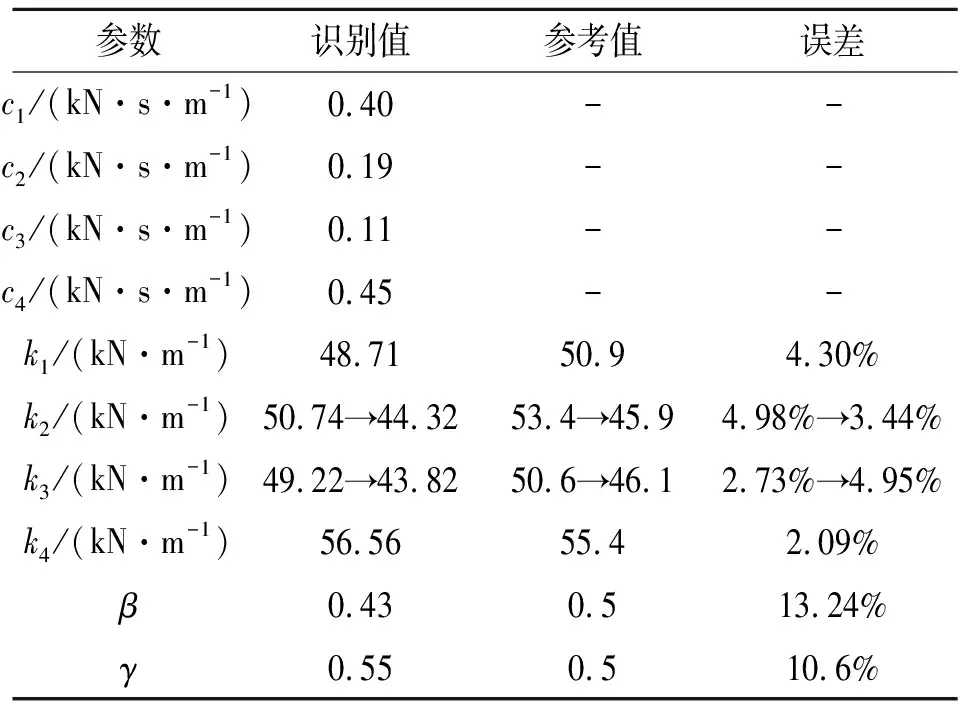
表1 实验识别结果(工况一)

在El Centro地震波激励下，AEKF-UI方法对基础隔震结构模型的参数及未知输入识别结果可知：刚度的识别精度较好，通常与有限元参考值的误差在5%以下，非线性迟滞参数的识别精度亦可以满足工程要求；该算法的收敛速度较快，且当结构发生损伤时，可以实时地追踪结构参数的变化；未知激励识别结果与传感器测得的结果相一致，能够有效地实现在线的未知输入反演。

2.3.2 工况二

基础隔震结构模型受Kobe地震波激励(滤波后频带[1.8～3]Hz，短持时高能量)，第二层和第三层SED所提供的有效刚度与工况一所提供的相同，在实验过程中，结构振动到t=12 s时，排出第三层的压缩空气，则第三层刚度从50.6 kN/m降低到46.1 kN/m，结构振动到t=20 s时，排出第二层的压缩空气，则第二层刚度从53.4 kN/m降低到45.9 kN/m，其他层刚度保持不变。在Kobe地震波激励下，测得的每层的绝对加速度响应ai如图4所示。

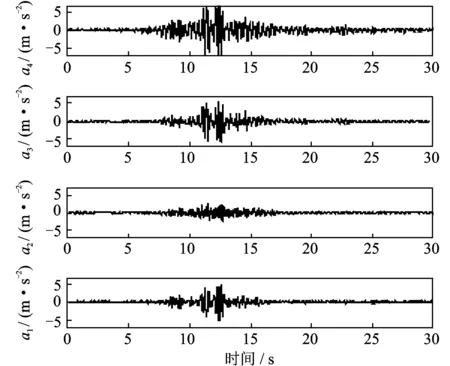
图4 测得的加速度响应(工况二)

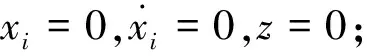
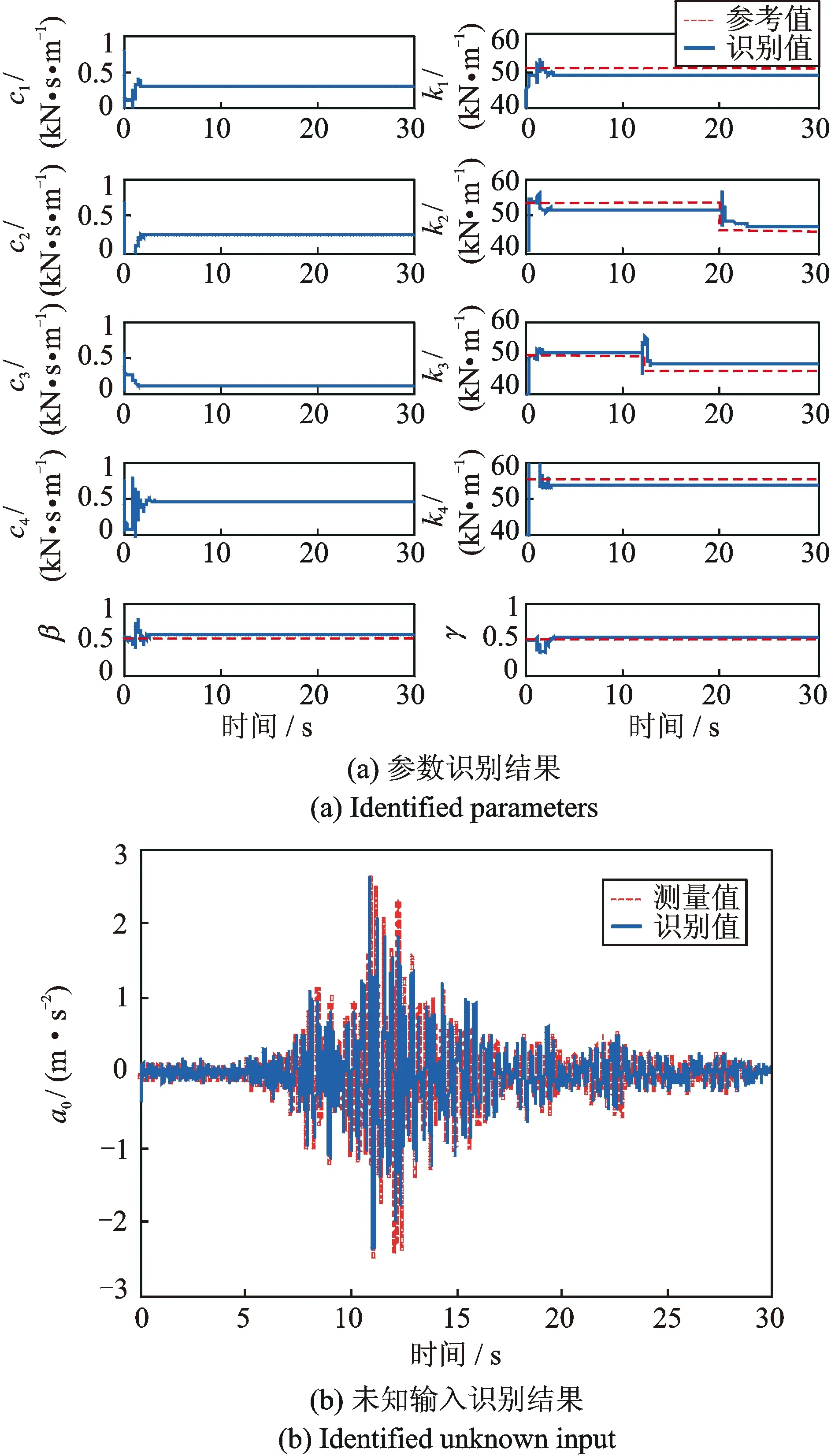
图5 实验识别结果(工况二)

在Kobe地震波激励下，AEKF-UI方法对基础隔震结构模型的识别结果可知：刚度及非线性迟滞参数识别值与参考值相一致，且参数识别结果与工况一中的识别结果相吻合；对不同于工况一中的损伤情况，该算法也可以有效地追踪结构参数变化；本工况下的未知输入识别结果误差略大于工况一中的识别结果，表明激励信号对识别结果精度有一定影响，综合分析两种工况中未知输入的识别结果可知该算法能够有效地识别未知输入。

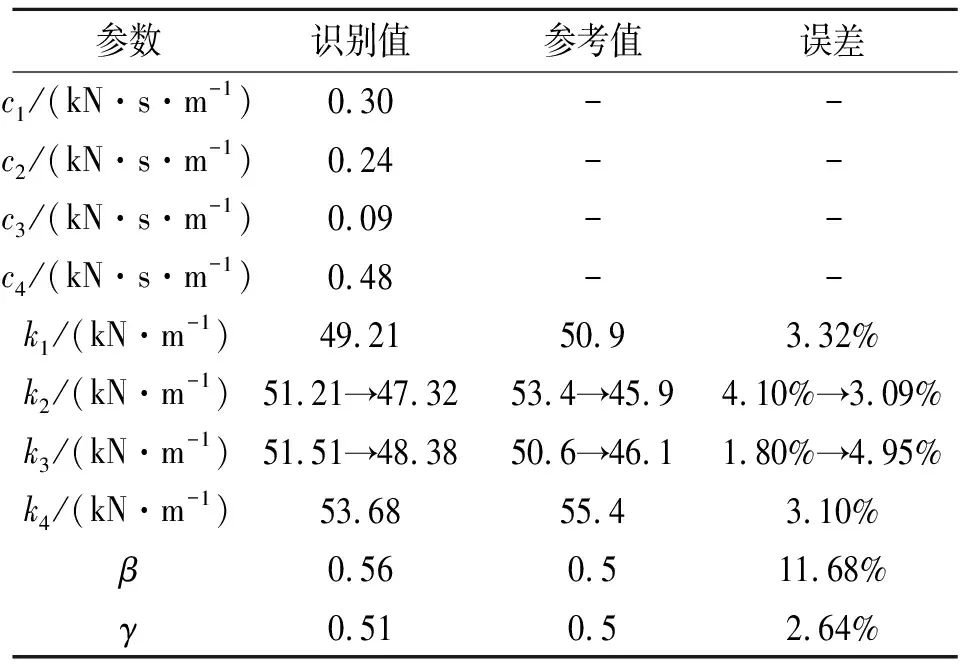
表2 实验识别结果(工况二)

3 结 论

本项研究发展了基于改进粒子群优化技术的AEKF-UI方法，以基础隔震结构模型为研究对象，在两种典型工况条件下对其进行振动实验。基于测得的加速度响应和AEKF-UI方法在线复合反演结构参数与未知输入，追踪结构损伤。实验研究结果表明：

(1)在两种典型地震波的激励下，采用AEKF-UI方法对基础隔震结构模型进行在线参数及未知输入识别，所得到的参数识别值与参考值相一致，且识别得到的未知输入与实验实测值吻合良好，验证了AEKF-UI方法复合反演结构参数与未知输入的可行性与有效性。

(2)通过时间、位置和程度不同的刚度突变模拟结构损伤，基于IPSO的自适应追踪技术能够实时地追踪结构参数变化，进而识别结构损伤，包括损伤的发生时间、位置和程度，表明了所发展的AEKF-UI方法具有较强的损伤追踪能力。

(3)AEKF-UI方法仅需测量系统的加速度响应即可实现结构参数及未知输入的识别，使得该方法在实际工程应用中易于实现；但由于算法过程中对状态方程进行了线性化处理，当初始参数估计超出了收敛范围时，识别结果可能会不收敛，通常需要预先进行仿真研究或根据经验确定合理的初始参数取值范围。

参考文献：

[1] Komodromos P. Seismic Isolation for Earthquake-resistant Structures [M]. Ashurst Lodge: WIT Press, 2000.

[2] Chang F K. Structural health monitoring [A]. Proceedings of 8th International Workshop [C]. Stanford, USA, 2011.

[3] Furukawa T, Ito M, Noori M N. System identification of base-isolated building using seismic response data [J]. ASCE Journal of Engineering Mechanics, 2005, 13(3): 268—273.

[4] 史东锋, 郑敏, 申凡, 等. 工程结构工作模态的子空间辨识方法[J]. 振动工程学报, 2000, 13(3): 406—412.Shi D F, Zheng M, Shen F, et al. Modal extraction of structure in operating conditions with subspace method [J]. Journal of Vibration Engineering, 2000, 13(3): 406—412.

[5] Ibrahim S R. Efficient random decrement computation for identification of ambient responses [A]. Proceedings of 19th IMAC [C]. Florida, USA, 2001, 4 359(1): 1—6.

[6] 续秀忠, 华宏星, 陈兆能. 基于环境激励的模态参数辨识方法综述[J]. 振动与冲击, 2003, 23(3): 1—5.Xu X Z, Hua H X, Chen Z N. Review of modal identification method based on ambient excitation [J]. Journal of Vibration and Shock, 2003, 23(3): 1—5.

[7] Humar J, Bagchi A, Xu H. Performance of vibration-based techniques for the identification of structural damage [J]. Structural Health Monitoring, 2006, 5(3): 215—241.

[8] Kozin F. Estimation of parameters for system driven by white noise excitation [A]. Proceedings of INTAM Symposium on Random Vibrations and Reliability [C]. Frankfurt Ioder, Germany, 1985: 163—173.

[9] Toki K, Sato T, Kiyono J. Identification of structural parameter s and input ground motion from response time history [J]. JSCE Structural Eng./Earthquake Eng., 1989, 6(2): 413—421.

[10] Doebling S W, Farrar C R, Prime M B. A summary review of vibration-based damage identification methods [J]. The Shock and Vibration Digest, 1998, 30(2): 91—105.

[11] 朱广荣, 陈国平, 张方, 等. 基于Wilson-θ算法的动载荷识别及影响因素[J]. 振动、测试与诊断, 2012, 32(5): 709—858.Zhu G R, Chen G P, Zhang F, et al. Dynamic load identification based on wilson-θ method and influence factors [J]. Journal of Vibration, Measurement and Diagnosis, 2012, 32(5): 709—858.

[12] Ling X, Haldar A. Element level system identification with unknown input with rayleigh damping [J]. Journal of Engineering Mechanics, 2004, 130(8): 877—885.

[13] Chen J, Li J. Simultaneous identification of structural parameters and input time history from output-only measurements [J]. Computational Mechanics, 2004, 33(5): 365—374.

[14] 王建有, 陈健云, 李宗坤, 等. 输入未知下非比例阻尼结构参数识别方法的研究[J]. 振动与冲击, 2007, 26(4): 119—125.Wang J Y, Chen J Y, Li Z K, et al. Study on identification method for a structure with non-proportional damping and unknown input [J]. Journal of Vibration and Shock, 2007, 26(4): 119—125.

[15] 张坤, 罗绍湘, 段忠东. 有限测点下结构参数与基底激励的同步反演 [J]. 振动工程学报, 2010, 23(1): 52—59.Zhang K, Law S S, Duan Z D. Simultaneous identification of structural parameters and support excitation from responses on limited degrees of freedom [J]. Journal of Vibration Engineering, 2010, 23(1): 52—59.

[16] 李杰, 陈隽. 未知输入条件下的结构物理参数识别研究[J]. 计算力学学报, 1997, 16(1): 32—40.Li J, Chen J. Study on identification of structural dynamic parameters with unknown input information [J]. Journal of Computational Mechanics, 1997, 16(1): 32—40.

[17] Yang J N, Pan S, Lin S. Least-squares estimation with unknown excitations for damage identification of structures [J]. Journal of Engineering Mechanics, 2007, 133(1): 12—21.

[18] Yang J N, Pan S, Huang H. An adaptive extended kalman filter for structural damage identifications II: unknown inputs [J]. Structural Control and Health Monitoring, 2007, 14(3): 497—521.

[19] 尹强, 周丽. 基于遗传优化最小二乘算法的结构损伤识别[J]. 振动与冲击, 2010, 29(8): 155—160.Yin Q, Zhou L. Structural damage identification based on GA optimized least square estimation [J]. Journal of Vibration and Shock, 2010, 29(8): 155—160.

[20] Zhou Y, Pei S. An effective adaptive multi-objective particle swarm for multimodal constrained function optimization [J]. Journal of Computers, 2010, 5(8): 1 144—1 151.

[21] 张铃, 张钹. 佳点集遗传算法[J]. 计算机学报, 2001, 24(9): 917—922.Zhang L, Zhang B. Good point set based genetic algorithm [J]. Chinese Journal of Computer, 2001, 24(9): 917—922.

[22] He Q, Wang L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems [J]. Engineering Applications of Artificial Intelligence, 2007, 20(1): 89—99.

[23] 李妮, 欧阳艾嘉, 李肯立. 求解约束优化的改进粒子群优化算法[J]. 计算机应用, 2012, 32(12): 3 319—3 325.Li N, Ouyang A J, Li K L. Improved particle swarm optimization for constrained optimization functions [J]. Journal of Computer Applications, 2012, 32(12): 3 319—3 325.

[24] Xia Q, Rao M, Ying Y, et al. Adaptive fading kalman filter with an application [J]. Automatica, 1994, 30(8): 1 333—1 338.

[25] Yang J N, Lin S, Huang H, et al. An adaptive extended kalman filter for structural damage identification [J]. Structural Control and Health Monitoring, 2006, 13(4): 849—867.

[26] 汪新明, 周丽. 基于振动响应的隔震支座的非线性建模及参数估计[J]. 振动与冲击, 2008, 27(1): 146—150.Wang X M, Zhou L. Modeling of a rubber bearing and its parameters estimation based of its dynamic response [J]. Journal of Vibration and Shock, 2008, 27(1): 146—150.

[27] Yin Q, Zhou L, Wang X. Parameter identification of hysteretic rubber-bearing based on sequential nonlinear least-square estimation [J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 9(3): 375—383.

[28] 周丽, 吴新亚, 尹强, 等. 基于自适应卡尔曼滤波方法的结构损伤识别实验研[J]. 振动工程学报, 2008, 21(2): 197—202.Zhou L, Wu X Y, Yin Q, et al. Experimental study of an adaptive extended kalman filter for structural damage identification [J]. Journal of Vibration Engineering, 2008, 21(2): 197—202.

[29] Ma F, Zhang H, Bockstedte A, et al. Parameter analysis of the differential model of hysteresis [J]. ASCE Journal of Applied Mechanics, 2004, 71(3): 342—349.

[30] Chen B J, Tsai C S, Chung L L, et al. Seismic behavior of structures isolation with a hybrid system of rubber bearings [J]. Structural Engineering and Mechanics, 2006, 22(6): 761—783.

[31] 尹强, 周丽. 基于EKF方法的橡胶隔震支座参数识别实验研究[J]. 南京航空航天大学学报, 2012, 44(1): 43—49.Yin Q, Zhou L. Experimental study on parameter identification of non-linear hysteretic rubber-bearing isolators using EKF method [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(1): 43—49.