强冲击载荷下钢筋混凝土路面动态响应影响因素敏感度分析

周晓和，马大为，仲健林，任杰

南京理工大学 机械工程学院，江苏 南京210094

0 引言

钢筋混凝土结构由于充分利用了混凝土的抗压性能和钢筋的抗拉性能，已被广泛地应用于高层建筑物、长跨桥、高速公路、水电站、隧道等。这些结构在其工作过程中除了承受正常的设计载荷之外，往往还要承受诸如爆炸、冲击和碰撞等动载荷，此时，受载结构处于大变形、高应变率和高静水压力状态;在远离动载荷作用处，围压效应减弱而多轴应力效应明显;介质内部由于拉、压应力波的相互作用对材料内部产生不同程度的破坏，对材料性能产生复杂的影响［2，3］。

文中对ABAQUS 有限元软件中混凝土塑性损伤模型的基本理论与特点进行介绍，并将其运用到钢筋混凝土建模中;结合参数化技术，通过对钢筋混凝土路面模型参数的修改，快速、准确地建立相应的非线性有限元动力学模型，并根据设定参数自动地进行计算，完成参数化求解目标，通过对计算结果的分析，对钢筋混凝土路面模型主要性能参数进行敏感度评估。

1 混凝土塑性损伤模型

ABAQUS 中的混凝土损伤塑性模型使用于模拟各种类型中的混凝土和其他准脆性材料，其采用各向同性弹性损伤结合各向同性拉伸和压缩塑性理论来表征混凝土的非弹性行为，可模拟低围压，混凝土受到单调、循环或动载作用下的力学行为，结合非关联多重硬化塑性和各向同性弹性损伤理论来表征材料断裂过程中发生的不可逆损伤行为。材料的弹性行为应为各向同性和线性的［5］。

1.1 屈服函数

模型考虑了在拉伸和压缩作用下材料具有不同的强度特征，考虑高围压力、等效应力以及有效最大主应力的影响，将材料的屈服函数写成式(1)的形式［4，5］:

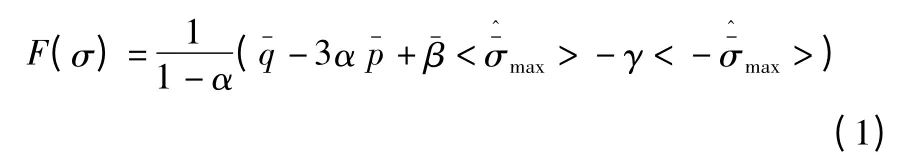
式中:α，β，γ—材料参数，由实验确定;

通过单轴压缩实验、等双轴压缩实验、单轴拉伸实验、TM(tensile meridian)实验、CM(compressive meridian)实验得到:

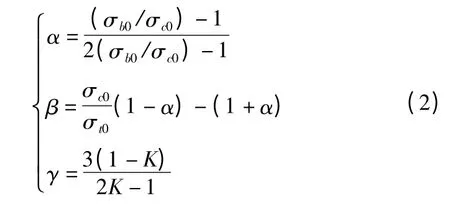
式中:σc0—单轴压缩实验的初始屈服点应力;

σb0—等双轴压力实验的初始屈服点应力;

σt0—单轴拉伸实验的初始屈服点应力;

σc—单轴压缩时的破坏临界应力;

1.2 混凝土的损伤行为描述

模型为连续的、基于塑性的混凝土损伤模型。它假设混凝土材料主要因拉伸开裂和压缩破碎而破坏。屈服或破坏的演化由两个硬化变量和控制。如图1 及图2 所示［4］。

图1 混凝土单轴拉伸下的应力应变关系

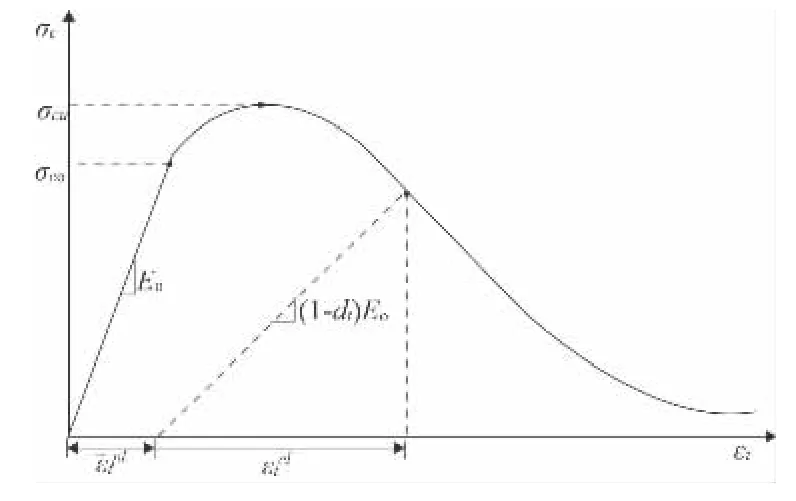
图2 混凝土单轴压缩下的应力应变关系

如果E0为材料的初始(无损)弹性刚度，则单轴拉伸和压缩载荷作用下的应力应变关系分别为:

1.3 流动势函数

混凝土损伤塑性模型采用非相关联势塑性流动。模型中采用的流动势G 为Drucker－ Prager 抛物线函数［4］，即:

ψ(θ，fi)为p－q 平面上高围压下的剪胀角;

ξ(θ，fi)为偏移量参数，给出了函数趋向于渐近线的速率。

2 有限元计算模型

有限元模型分为两层:1)钢筋混凝土层;2)土基。钢筋混凝土层采用混凝土与钢筋分离的方法建模，有限元模型尺寸为5.4 m×4 m ×0.24 m。混凝土的模拟采用混凝土塑性损伤模型，根据文献［1］提供的数据，定义材料的力学行为;钢筋采用Mises 弹塑性模型，用埋入(Embedded)的方式将钢筋放置在距混凝土表面0.11 m 的位置。第二层为土基层，有限元尺寸为5.4 m ×4 m ×2 m。各层材料参数见表1、表2;钢筋混凝土层与土基层之间不考虑层间断裂效应，四周设置为自由，土基底面设置为固端约束。钢筋混凝土路面中心处加载，加载半径R=0.4 m;加载时间t=8 ms，载荷最大值14 MPa，单次载荷总作用时间T=0.1 s。

表1 混凝土塑性参数

表2 各层材料参数

3 计算结果及分析

运用参数化技术，通过自编钢筋混凝土路面参数化仿真软件，对混凝土厚度、纵向配筋率及钢筋位置三项参数逐一进行参数化计算，从而对单个参数敏感度进行分析。

3.1 混凝土板厚度

当钢筋混凝土路面模型纵向配筋率、钢筋位置等参数相同时，分析混凝土板厚度对路面在强冲击载荷下动态响应的影响。分析模型如表3 所示。

表3 不同混凝土厚度有限元分析模型

图3、图4 为计算后得到的不同混凝土厚度情况下钢筋混凝土路面的载荷中心点最大沉降值及板底中心最大应力。

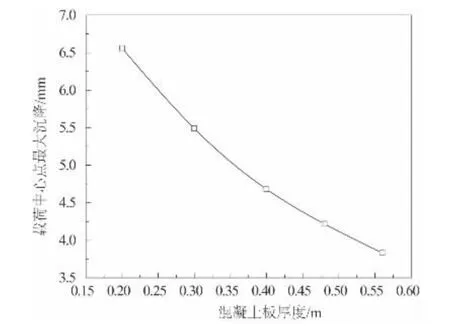
图3 载荷中心点最大位移随混凝土板厚度变化曲线

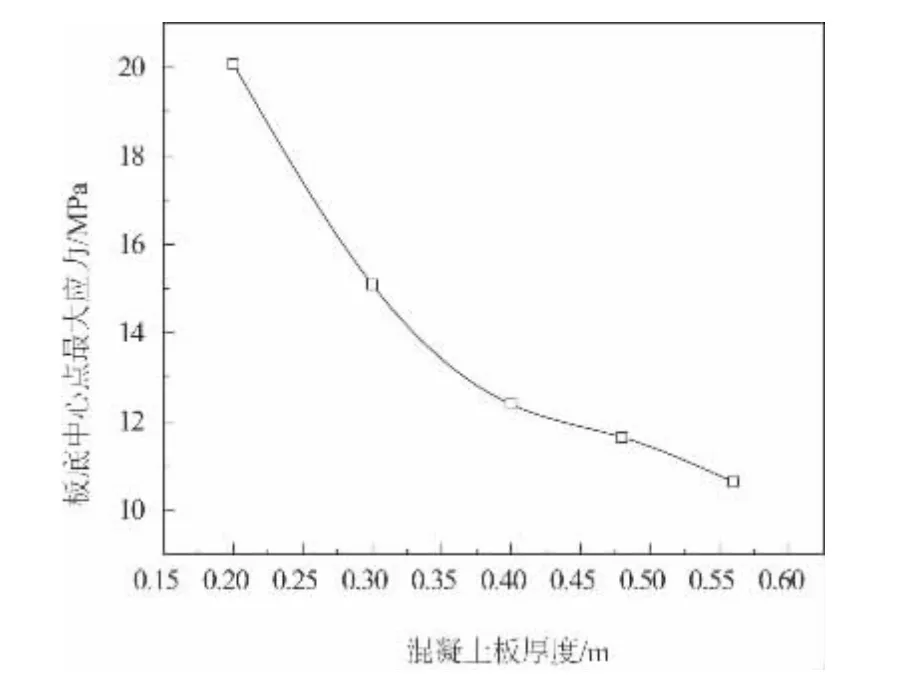
图4 板底中心点最大应力随混凝土板厚度变化曲线

通过图3 及图4 可以看到:1)随着混凝土板厚度的增加，载荷中心点最大沉降值减小。混凝土板厚度从开始的0.2 m 变至0.3 m，加载中心点最大位移减小了16.3%;厚度从0.3 m 变至0.4 m，最大位移减小了14.8%;厚度从0.4 m 变至0.48 m，最大位移减小了9.8%;厚度从0.48 m 变至0.56 m，最大位移减小了9.2%。故随着混凝土板厚的增大，加载中心点最大位移变化率变小。

2)随着混凝土板厚度的增加，板底中心点最大应力逐渐减小。当混凝土板厚度H ＞0.4 m 之后，随着板厚的进一步加大，板底中心点最大应力值的变化趋于平稳。故得到随着混凝土板厚的增大，板底中心点最大应力变化率变小。

3.2 纵向配筋率

影响纵向配筋率大小主要有两方面因素:钢筋直径与钢筋间距。对混凝土厚度及钢筋位置等参数相同的钢筋混凝土路面，选取8 个不同纵向配筋率钢筋混凝土路面模型进行研究，计算结果如表4 及图5 所示。

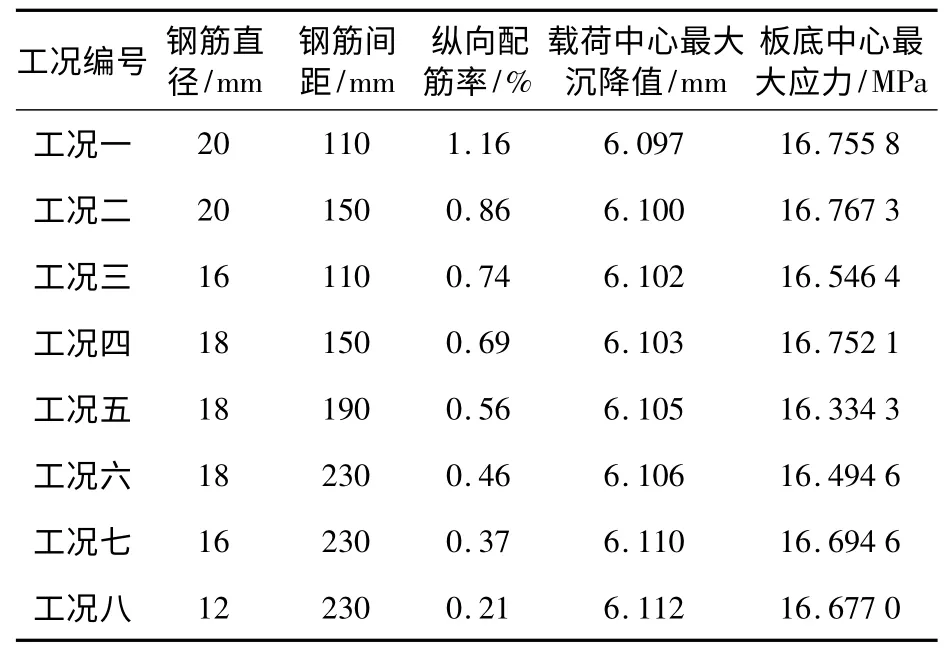
表4 不同纵向配筋率有限元分析工况及结果

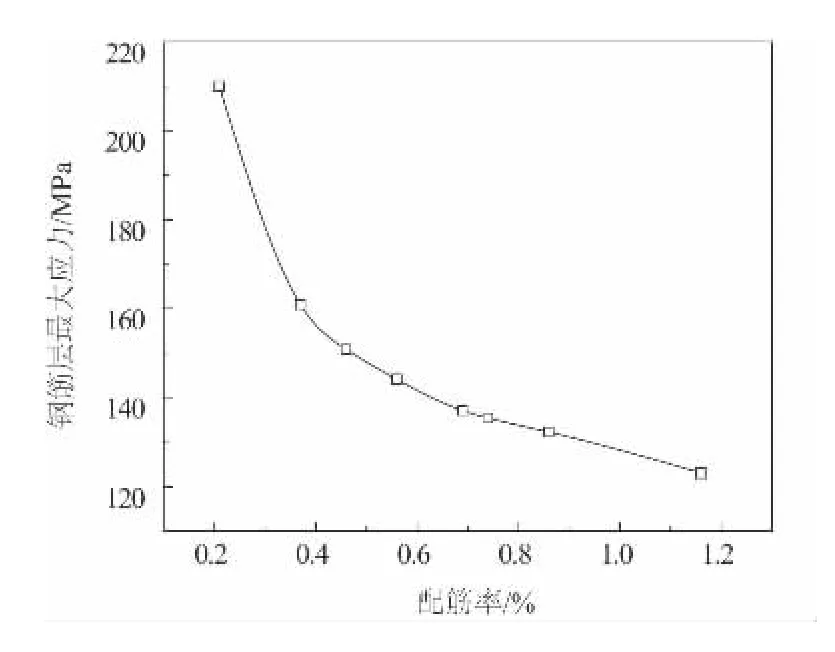
图5 钢筋层最大应力随纵向配筋率变化曲线

通过表4 及图5 可以看到:1)随着配筋率的减小，载荷中心点最大位移逐渐增大，但变化值非常小;在8 个工况中，板底中心最大应力的变化并无明显规律，且计算结果中最大值与最小值间仅相差2.6%。说明纵向配筋率的增加对加载中心最大位移及板底中心最大应力无太大影响。原因为设置钢筋网的主要目的并非是为了增加板的抗弯强度，而是为了将开裂的混凝土落在一起，使板依靠断裂面的集料嵌锁作用保证结构的强度。

2)随着配筋率的增大，钢筋层最大应力明显下降，应力在钢筋层中更加平均，提高了钢筋混凝土层的结构强度。但是当配筋率λ ＞0.4%之后，随着配筋率的进一步增大，钢筋层最大应力减小幅度减缓，此时纵向配筋率的提高对钢筋混凝土路面的抗冲击性能提高起到的作用也越来越有限。

3.3 钢筋位置

当钢筋混凝土路面模型纵向配筋率、混凝土厚度等参数相同时，分析钢筋位置对路面在强冲击载荷下动态响应的影响。分析模型及工况计算结果如表5 所示。

表5 不同钢筋位置有限元分析工况及结果

通过表4 及表5 可以看到:

1)随着钢筋距顶面距离的增大，载荷中心最大沉降值在减小，但变化值不大。

2)通过表5 工况计算结果发现，钢筋层靠近面板顶层和靠近面板底层的板底中中心最大应力值都比较大;钢筋层在混凝土板2/3～1/2 之间时，板底中心最大应力值比较小。故通常将钢筋层放置于混凝土层中间位置比较合理。

4 结论

1)强冲击载荷下，混凝土层厚度对钢筋混凝土路面载荷中心沉降值及板底中心最大应力值影响较大。随着混凝土层厚度的增加，载荷中心最大位移值及板底中心最大应力值均减小，并且载荷中心最大位移变化率及板底中心最大应力变化率均减小。

2)强冲击载荷下，钢筋层位置对钢筋混凝土路面载荷中心沉降值有规律性影响，但影响不大，但是钢筋层位置对钢筋混凝土板底应力有较大影响。钢筋层靠近钢筋混凝土面板顶层和面板底层的板底中心点应力均比钢筋层处在中间位置的板底中心点应力要大，故将钢筋层设置在混凝土层2/3～1/2 比较合理。

3)强冲击载荷下，纵向配筋率的变化对钢筋混凝土载荷中心最大沉降值影响不大，并且对钢筋混凝面板板底应力的影响并无明显规律。但是，随着配筋率的提高，钢筋层内最大应力降低，钢筋混凝土内部应力更加均匀，提高了钢筋混凝土路面的结构强度;当配筋率λ ＞0.4%之后，随着配筋率的进一步增大，钢筋层最大应力减小幅度减缓。

［1］刘文晶，姚婵娟，刘涛等.冲击荷载作用下混凝土路面的损伤分析［C］.中国公路学会公路环境与可持续发展分会2010 年学术年会论文集.2010 .

［2］朱聪.碰撞冲击荷载下钢筋混凝土结构的动态响应及损伤机理［D］.天津:天津大学，2011.

［3］梁星文，叶艳霞.混凝土结构非线性分析［M］.北京:中国建筑工业出版社.2007.

［4］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京:清华大学出版社.2004.

［5］王金昌，陈页开.ABAQUS 在土木工程中的运用［M］.杭州:浙江大学出版社.2006.