基于GA-PIDNN 的液压弯辊控制系统设计

张秀玲，徐腾，赵亮，樊红敏，臧佳音

(1. 燕山大学 河北省工业计算机控制工程重点实验室，河北 秦皇岛，066004；2. 国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛，066004)

板形是板带钢的重要质量指标，板形控制是板带轧机的关键技术。建立稳定、精确、快速的板形控制模型已成为板形控制技术发展的迫切要求[1]。在板形控制系统中，液压弯辊控制是影响板形二次分量的主要因素[2]，液压弯辊力响应的快速性和精准性对整个板形控制系统的性能起着至关重要的作用。现阶段液压弯辊控制系统多采用常规的PID 控制算法，但是实际系统具有时变性和非线性等特点，而且随机干扰严重，难以建立较准确的数学模型，实践证明传统PID控制难以获得满意的控制效果[3]。因此，采用现代控制方法(如预测控制、最优控制等)和智能控制方法(如专家系统、神经网络等)相结合的手段，已成为板形控制系统的发展趋势[4]。陈丽等[5]提出的FNN 模型参考自适应控制和张秀玲等[6]提出的RBF 网络板形预测控制等，这些新方法提高了板形质量，促进我国高精技术制造业的发展。但是存在原理复杂、结构繁琐等缺陷，需要对其进行深入研究寻求更简捷易行的控制方法。目前应用较多的神经元模型，一般只考虑了神经元的静态特性，只能处理静态信息。对于动态信息的处理，主要通过神经元网络互联方式的动态结构进行。PID神经网络(PIDNN)是由Shu等[7]提出的一种新型网络，隐含层神经元中，不仅具备静态非线性映射功能的比例元，而且可处理动态信息的积分元和微分元。PIDNN 是固定2×3×1 结构，避免了优化选择隐含层神经元个数的过程。PIDNN 控制器是将神经网络和PID 控制规律融为一体，既具有神经网络自学习、自适应的功能，又具有常规PID 控制器结构简单、参数物理意义明确的优点[8]，并且不需要测量或辨识对象的内部结构和参数，非常适用于复杂的被控对象。本文在文献[9]的基础上结合GA 全局寻优的特点，设计了基于GA-PIDNN 的控制器，利用GA 代替BP 算法修正PIDNN 权值。以某900HC 四辊轧机液压弯辊控制系统为例，对其进行了仿真对比实验。

1 基于GA 的PIDNN 优化设计

1.1 PIDNN 结构及工作原理

液压弯辊系统是单输入单输出系统，控制该系统，只需要1 个PIDNN(SPIDNN)。其拓扑结构如图1 所示[10]。

SPIDNN 的前向算法如下。

输入层有2 个比例神经元，输入分别为被控量的给定值和实际值。在任意采样时刻k，其输入为

输入层神经元的状态为

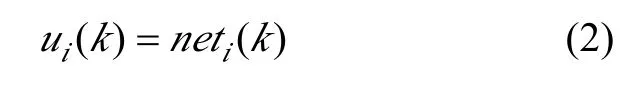
输入层神经元的输出为

式中：i=1,2。隐含层是神经网络中最重要的层次，SPIDNN 的隐含层有3 个神经元，分别为比例元、积分元和微分元，它们各自的输入为

比例元的状态为

积分元的状态为

微分元的状态为

隐含层各神经元的输出为

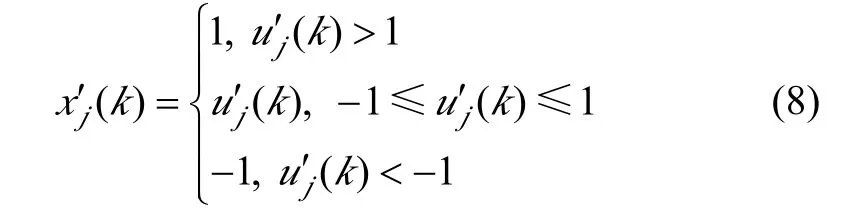
式中：j=1,2,3；wij为输入层至隐含层的连接权重值。

输出层有1 个神经元，完成网络的总和输出功能，其输入为

输出层神经元的状态函数与比例元的状态函数相同，状态为

输出层神经元的输出为

而SPIDNN 的输出 v (k)就等于输出层神经元的输出，即

式中： w′j为隐含层至输出层的连接权重值。

1.2 GA 优化PIDNN

GA 是一种基于生物遗传和进化机制的适合于复杂系统优化的自适应概率优化技术[11]。GA 借鉴了达尔文进化论和孟德尔遗传学说，模仿生物遗传与进化机制，在固定种群规模中，对于具体问题进行染色体编码，根据生物进化的选择、交叉、变异因子等基本操作，产生新种群，得到最适合环境的个体，即最符合优化要求的染色体代码，使群体进化到搜索空间中更好的区域，如此不断繁衍进化，最后收敛到一群最适应环境的个体，通过解码求得问题的最优解[12]。GA与传统寻优方法和其他搜索方法有很大不同，最主要的区别是GA 以一组可行解为起点全局寻优，而其他方法在搜索空间中从一个点出发[13]。GA 优化流程如图2 所示。本文作者采用的PIDNN，包括9 个权值，即9 个变量，采用实数编码方法对其每个参数进行编码，码串中包括输入层至隐含层的权值及隐含层至输出层的权值，如其中某一码串可写为：(0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9)。

图2 GA 的基本流程图Fig.2 Process of genetic algorithm

GA 运行参数需要预先设定，包括群体大小、GA终止进化代数、交叉概率、变异概率，本文利用GA工具箱，选择初始群体大小为20，交叉概率为0.8，变异概率自适应调整范围0.01～0.1。GA 工具箱中以求适应度函数最小值为优化目标[14]，所以取网络误差平方为适应度函数。为达到控制要求GA 终止条件为适应度函数达到最小，GA 在遗传代数达到120 代时结束，此时适应度函数值为3.697 9×10-5，适应度函数值变化曲线及最优个体如图3 所示。GA 优化得到 的 PIDNN 权 值 为 w=[4.640 778 733 126 01,8.714 444 759 873 39,1.493 657 123 164 90,-1.407 261 160 785 11,14.943 934 511 553 0,3.217 539 431 226 30, 30.119 752 166 772 3,37.696 235 537 772 5,-0.432 580 167 496 972]。

使用BP 算法优化PIDNN 权值，其误差平方曲线如图4 所示，优化后的权值为w=[2.726 540 746 656 00,2.099 856 150 367 00,-2.968 661 938 620 00,-21.808 020 028 176 0,-72.852 575 854 975 0,2.942 897 941 130 00, -23.963 145 443 672 3,-44.380 911 612 162 3,-2.268 926 167 558 37]。

图4(a)中BP 算法陷入局部极小值，不能达到控制要求。图4(b)中BP 优化算法虽能够减小误差，但具有随机性，并且BP 优化PIDNN 的学习时间较长，优化结果与初始权值的选择有很大关系，GA 具有全局寻优特点，克服了BP 算法的不足，使液压弯辊力控制系统达到理想控制效果。

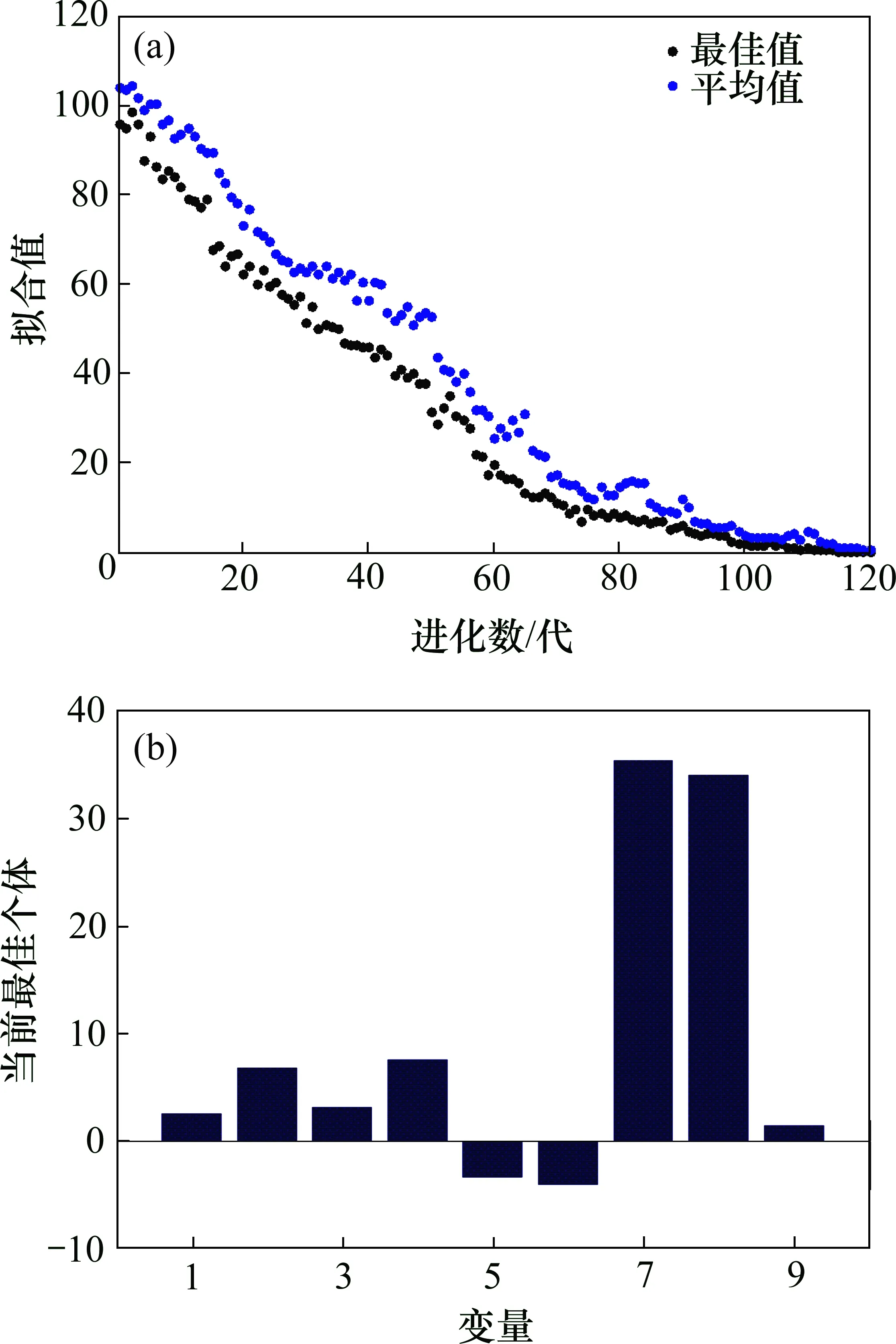
图3 GA 优化过程及优化结果Fig.3 Process and results of GA’s optimization

图4 PIDNN 的BP 优化训练误差平方曲线Fig.4 Squared error’s curves of training of PIDNN optimized by BP algorithm

1.3 GA-PIDNN 液压弯辊控制系统设计

传统的液压弯辊控制系统主要包括伺服放大器、伺服阀、液压缸和压力传感器等几部分[15]。其原理如图5 所示。

本文设计的GA-PIDNN 液压弯辊控制系统对伺服阀及液压缸进行控制，控制结构如图6 所示。

SPIDNN 输入层的输入分别为弯辊力给定值和弯辊力实际输出值。神经网络控制器的输出端与伺服阀的输入端相连，u 为液压弯辊系统的控制输入，控制伺服阀的容积流量，伺服阀输出控制液压缸弯辊力输出。SPIDNN 通过GA 修正网络权值，以误差平方作为适应度函数，利用GA 工具箱对网络权值进行优化。

图5 弯辊力控制系统原理图Fig.5 Schematic diagram of bending force control system

图6 GA-PIDNN 液压弯辊控制系统Fig.6 Structure of hydraulic bending force control system

3 仿真验证

以某900HC 四辊可逆轧机液压弯辊控制系统为研究对象，由机理建模可知，该系统是一个复杂的高阶系统，为便于研究取其离散化模型[16]

式中： F (k)为液压系统输出的弯辊力；u (k)为控制器的输出；ξ(k)为系统的随机干扰。

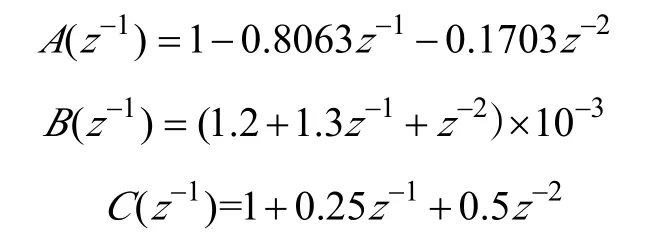
以此模型为受控对象，分别使用GA 和BP 算法优化SPIDNN，弯辊力设定为14 kN，在随机干扰情况下，仿真结果如图7 所示。

图7 SPIDNN 液压弯辊力控制仿真曲线Fig.7 Simulation curves of hydraulic bending force control based on SPIDNN

从图7 可见：1) 在扰动情况下，PIDNN 控制器使系统输出在目标值附近振荡，总体获得较好的控制效果；2)BP 算法易陷入局部极小值，达不到控制要求；3) 与BP 算法比较，在同样的仿真条件下GA 所优化的PIDNN 控制器能够使输出更快的达到目标值，具有很好的快速性。

4 结论

由于GA 具有全局寻优的特点，其遗传算子易于操作，通过GA 优化的PIDNN 液压弯辊控制系统优于BP 算法优化的控制效果，显示了GA-PIDNN 控制器的快速性和有效性，克服了常规PIDNN 控制的不足，进一步证实了GA-PIDNN 不仅结构简单并且具有优于其它神经网络的动态性能，利于在控制领域中的推广应用。

[1] 张材, 谭建平. 基于遗传算法反向传播模型的板形模式识别[J]. 中南大学学报(自然科学版),2006,37(2):294-299.ZHANG Cai, TAN Jianping. Strip flatness pattern recognition based on genetic algorithms-back propagation model[J]. Journal of Central South University (Science and Technology), 2006,37(2):294-299.

[2] CAO Jianguo,XU Xiaozhao,ZHANG Jie,et al.Preset model of bending force for 6-high reversing cold rolling mill based on genetic algorithm[J]. Journal of Central South University of Technology,2011,18(5):1487-1492.

[3] 王志勇, 郑德忠. 基于广义预测控制的液压弯辊控制系统[J].重型机械,2006(5):8-11.WANG Zhiyong, ZHENG Dezhong. The hydraulic roll bending control system based on the generalized predictive control[J].Heavy Machinery,2006(5):8-11.

[4] 陈丽, 李建更, 乔俊飞, 等.UC 轧机二次型板形缺陷模糊神经网络控制[J]. 控制工程,2005,12(5):438-441.CHEN Li, LI Jiangeng, QIAO Junfeil, et al. Fuzzy neural network control for shape defects of quadratic form of UC rolling mill[J]. Control Engineering of China, 2005, 12(5):438-441.

[5] 陈丽, 李建更, 乔俊飞, 等.FNN 模型参考自适应控制在轧机液压弯辊系统中的应用[J]. 计算机测量与控制,2005,13(12):1396-1399.CHEN Li, LI Jiangeng, QIAO Junfei, et al. Fuzzy neural network model reference adaptive control method for the hydraulic roll bending in the control system of UC rolling mill[J].Computer Measurement&Control,2005,13(12):1396-1399.

[6] 张秀玲, 陈丽杰, 逄宗朋, 等.RBF 神经网络的板形预测控制[J]. 智能系统学报,2010,5(1):70-73.ZHANG Xiuling, CHEN Lijie, PANG Zongpeng, et al. A predictive system for process control of flatness in rolling mills using a radial basis function network[J]. CAAI Transactions on Intelligent Systems,2010,5(1):70-73.

[7] SHU Huailin, PI Youguo. PID neural networks for time-delay systems[J]. Computers and Chemical Engineering, 2000:859-862.

[8] 舒华, 舒怀林. 基于LabView 的PIDNN 控制器设计与仿真[J].系统仿真学报,2006,18(10):2918-2920.SHU Hua,SHU Huailin.Development and simulation of PIDNN controller based on LabView[J]. Journal of System Simulation,2006,18(10):2918-2920.

[9] 王益群, 孙福.PIDNN 在电液弯辊伺服控制系统中的应用[J].机床与液压,2008,36(3):83-85.WANG Yiqun, SUN Fu. Application of PID neural network in electro-hydraulic bending control system[J]. Machine Tool &Hydraulics,2008,36(3):83-85.

[10] 舒怀林.PIDNN 及其控制系统[M]. 北京: 国防工业出版社,2006:21-25.SHU Huailin. PIDNN and control system[M]. Beijing: National Defense Industry Press,2006:21-25.

[11] Tang K S, Man K F, Wong S K. Genetic algorithm and their applications[J]//IEEE Signal Process,1999,13(6):22-37.

[12] SHI Haiyan. Parameters estimation of continuous system using improved hybrid genetic algorithm[J]. Journal of Information and Computational Science,2009,5(5):2285-2291.

[13] Ga´bor Renner, Aniko Ekart. Genetic algorithms in computer aided design[J].Computer-Aided Design,2003(35):709-726.

[14] 雷英杰, 张善文, 李续武, 等.MATLABGA 工具箱及应用[M].西安: 西安电子科技大学出版社,2005:160-178.LEI Yingjie, ZHANG Shanwen, LI Xuwu, et al. MATLAB GA toolbox and application[M]. Xi’an: Xi’an University of Electronic Science and Technology Press,2005:160-178.

[15] 曾春峰. 液压弯辊系统对板凸度影响的实验研究[D]. 秦皇岛:燕山大学机械工程学院,2011:31-39.ZENG Chunfeng. The experimental study of hydraulic roll bending system’s effect on plate crown[D]. Qinhuangdao:Yanshan University. College of Mechanical Engineering, 2011:31-39.

[16] 张秀玲, 刘宏民. 液压弯辊系统的智能内膜控制[J]. 电工技术学报,2002,17(1):91-95.ZHANG Xiuling, LIU Hongmin. Intelligent internal model control for hydraulic roll bending system[J]. Electrical Technology Journal,2002,17(1):91-95.