公路连续刚构桥梁车桥耦合共振判定方法

王凌波，蒋培文，康馨，马印平，周勇军

(1. 长安大学 公路学院，陕西 西安，710064；2. 陕西省交通厅 基本建设工程质量监督站，陕西 西安，710075；3. 密苏里科技大学 土木工程学院，美国 密苏里，65401)

移动车辆通过桥梁时会与桥梁结构产生耦合振动，该问题的研究起源于19 世纪中后期。Dahlberg等[1-2]对客运专线和高速铁路桥梁车桥相互作用的理论及其应用进行了研究，先后建立了各具特色的车桥振动分析模型，使车桥耦合振动的研究取得了很大进展。国内对车桥耦合振动的研究同样起始于铁路桥梁，李国豪[3]以列车荷载通过悬索桥为工程背景，进行了桥梁的强迫振动等方面的研究。夏禾[4]较全面地研究了车辆与结构动力相互作用的分析理论、分析方法及其工程应用。而对于公路桥梁，早期学者往往由于公路交通荷载较小而忽略车桥振动问题。随着我国公路交通建设的飞速发展，车辆载重及行驶速度均显著提高，公路桥梁的车桥耦合振动问题已逐渐受到国内外众多学者的广泛关注。谢旭等[5]以大跨斜拉桥为研究对象，应用考虑拉索侧向振动影响的车桥耦合振动分析方法研究了钢索和CFRP 索斜拉桥的交通振动响应。肖永刚等[6]采用移动振动模型，考虑桥梁的几何非线性影响因素，建立了车桥耦合系统的运动微分方程并分析了非线性因素对桥梁跨中最大位移的影响。叶茂等[7]将桥梁简化为两端简支的欧拉-伯努梁模型，以桥面不平度功率谱密度函数作为输入参数，建立了多个移动车辆系统与桥梁间的耦合力学分析模型，并研究了多种工况作用下桥梁跨中位移均方根的变化规律。陈榕峰等[8-9]采用多次迭代的方法对车桥耦合振动响应进行求解，效果良好。郭文华等[10-11]对斜拉桥、连续桥梁在不同影响因素下的车桥耦合响应进行了研究。连续刚构体系桥梁跨越能力较大，施工周期较短，设计施工技术较成熟，目前已在我国公路交通建设中广泛使用。车桥耦合共振作为车桥耦合振动时一种特殊的小概率现象，人们对复杂多变的公路交通荷载是否存在与桥梁结构产生共振的可能性以及共振判定方法的研究很少。由于共振效应会使荷载效应在一定时间内成倍增长，对桥梁结构造成损伤甚至破坏，故即使现行规范中连续刚构桥梁车辆静力荷载较小、大跨结构冲击系数较低，对其进行车桥耦合共振效应研究也具有十分重要的意义。为此，本文作者首先提出车桥耦合振动的通用建模分析方法，进而应用该方法对公路连续刚构桥梁进行车桥耦合共振效应的研究。

1 车桥耦合振动建模分析方法

1.1 基于ANSYS 的分析方法

1.1.1 ANSYS 车桥模型的建立

本文方法将车辆模型与桥梁模型建立于同一个ANSYS 工作环境下，但两者之间无任何直接联系，各自独立，两者间耦合作用关系通过APDL 编程语言实时计算。在此以五自由度三轴车辆为例进行研究，模型及车辆参数如图1 所示。图1 中：mc为车体质量；Ic为车体质心绕z 轴转动惯矩；mi，kui，kdi及cui，cdi(i=1,2,3)分别为各车轮处的质量、刚度及阻尼参数；b1和b2分别为车体质心距后轴、前轴的距离；b3和b4分别为中轴距后轴、前轴的距离；c1为驾驶员位置处距前轴的距离。

图1 五自由度三轴车辆模型Fig.1 Model for 3 axes 5 degrees freedom vehicle

当多辆车以不同行驶参数作用于桥梁时，可在ANSYS 环境下建立多个相互独立的车辆模型，以进行多车辆过桥时的耦合振动分析。也可将各种不同工况对应的桥梁及车辆在同一ANSYS 环境下建模，并结合APDL 语言通过1 次计算得到所有计算结果。

1.1.2 确定车辆各轮在任意时刻的坐标

采用车辆行驶时前轮的起始点M与结束点N来定义车辆的行驶方向(M 点的空间坐标为(Mx，My，Mz)，N 点的空间坐标为(Nx，Ny，Nz))，结合车辆的初始速度v0、车辆的加速度a、车辆的行驶时间t，可确定匀速或匀变速行驶时的车辆模型各轮坐标。以图1 所示的三轴车为例，各轮位置坐标计算结果为

1.1.3 车轮位置与桥梁相关节点的竖向荷载与挠度转换

1) 车轮位置最近节点的等效荷载。梁单元的等效荷载转换示意图如图2 所示，梁单元等效荷载可根据参考文献[12]进行计算，结果为

2) 车轮位置处的竖向位移。梁单元位移转化示意图如图3 所示，纯弯梁单元的位移场(竖向挠度)推导结果为[12]

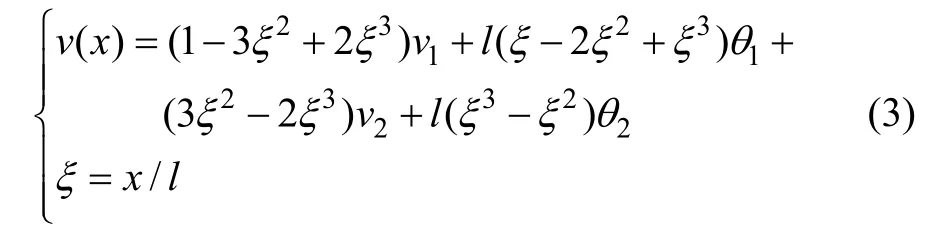
此外，扭矩的荷载及位移转换可根据线性插值进行计算[12]。

1.1.4 车桥耦合相互作用的数值计算方法

以图1 所示的三轴车辆模型为例，该模型的车辆位移列阵Zv包含的5 个独立自由度分别为车体的竖向位移zc与转角rc以及车轮处的竖向位移z1，z2和z3。车辆模型的振动方程为

图2 梁单元的等效荷载转换示意图Fig.2 Diagram of equivalent load transformation

图3 梁单元位移转化示意图Fig.3 Diagram of displacement transformation

其中：Mv为车辆质量矩阵；Kv为车辆刚度矩阵；Cv为车辆阻尼矩阵；Gv为重力荷载向量；Fbv为耦合荷载向量。

由结构动力学可知，Mv(Cv，Kv)的第i 行第j 列元素的物理意义为：由第j 自由度处的单位加速度(速度、位移)引起的第i 自由度处的力。故当车辆行驶于桥面时，车辆模型底部支撑即车桥接触点产生竖向位移，但该位移变化与Mv，Kv，Cv和Gv并无关联，由此可见车辆振动方程中仅有Fbv随时间及车辆位置变化。以图1 所示的三轴车辆模型为例，易得Fbv为

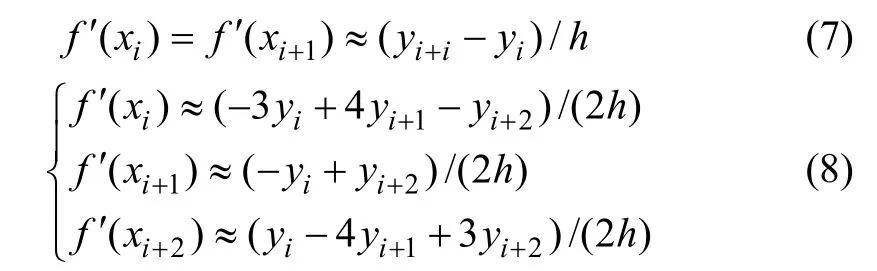
根据以上算法，结合有限元建模理论[13-16]编写《公路桥梁车桥耦合振动响应计算系统》。该系统可以实现的主要功能如图4 所示，系统主要界面如图5 所示。

图4 系统功能示意图Fig.4 Software function

图5 系统界面示意图Fig.5 Software interface

1.2 车辆匀速通过简支梁时的车桥耦合振动分析

车辆与简支梁的参数按照参考文献[3]取值，依据本文方法进行建模计算，将结果进行整理并与文献[3]中半解析法得到的结果插图进行对比，如图6 所示。

1.3 车桥耦合振动实桥测试

以陕西某座实桥为工程背景进行车桥耦合振动响应测试，该桥上部结构为(75+140+75)m 预应力混凝土连续刚构，最大墩高49.0 m，下部结构为空心墩及桩基础。以3 辆三轴重车依次以30 km/h 行驶过桥工况为例，得到实测中跨跨中竖向位移时程曲线与本文方法计算结果对比，如图7 所示。

经对比表明，本文基于ANSYS 平台的分析结果与参考文献及实测结果吻合良好，通过自开发软件，只需对桥梁结构进行建模结合输入的计算参数即可对多种工况的车桥耦合振动响应进行求解，并具有较高的精度及良好的适用性。

2 连续刚构车桥耦合共振判定方法

共振是指结构所受激励的频率与结构的某阶固有频率相接近时，结构振幅显著增大的现象。共振通常会引起结构很大的变形和动应力，甚至造成破坏性事故，工程史上不乏实例。公路连续刚构桥梁的设计及施工技术已日趋成熟，其最大跨径超过300 m，最大墩高超过150 m，对于此类低基频高墩大跨桥梁结构，现行规范对应的冲击系数极低，而对于低基频结构车桥耦合共振的可能性及判定方法研究很少。这里以1座高墩大跨连续刚构桥梁为背景，研究公路连续刚构桥梁的车桥耦合共振效应及判定条件。

2.1 桥梁与车辆模型

以1 座大跨预应力混凝土连续刚构桥梁为研究对象。跨径组合为(100+160+160+100)m，主梁采用单箱单室截面，跨中处梁高为3.0 m，支点处梁高为9.0 m，桥面宽度为13 m，按双车道加紧急停车带设计。桥墩采用6.5 m(宽)×6.0 m(高)空心薄壁墩，墩高为100 m，该桥梁有限元模型如图8 所示。行驶车辆采用三轴车辆模型，车辆参数见表1。

图6 位移分析结果与文献[3]中结果对比Fig.6 Displacement of comparison between calculated results and results in Ref.[3].

图7 跨中位移时程曲线Fig.7 Displacement of displacement time curves at mid-span

图8 桥梁有限元模型Fig.8 Finite element model of bridge

车轴 构量架轮m/对kg质车体旋转刚度Ic/(kg·m2)前轴8001.6221.96×1052.7399.80×1041.6×1043.822×105中轴1 6003.2443.92×1055.4781.96×1051.6×1043.822×105后轴1 6003.2443.92×1055.4781.96×1051.6×1043.822×105一系垂向刚度ku/(MN·m-1)一系垂向阻尼cu/(kg·s-1)二系垂向刚度kd/(MN·m-1)二系垂向阻尼cd/(kg.s-1)车体质量mc/kg

2.2 单车辆车桥耦合共振判定方法

对连续刚构桥梁各截面的影响线进行计算后发现，主梁截面的影响线无明显的周期性，且沿桥面方向衰减较快，见图9。而桥墩截面的影响线则具有比较明显的周期性，且沿桥面方向几乎无衰减，见图10。

对于单车辆匀速行驶过桥工况，其对于某截面的荷载效应时程曲线形状与相应的影响线形状类似。故对于主梁截面，车辆匀速过桥并不产生周期性荷载效应；而对于主墩截面，车辆匀速过桥则会产生周期性荷载效应，当此周期性荷载效应的频率接近桥墩振动基频时，即可能发生共振。

图9 主梁中跨4 分点弯矩影响线Fig.9 Moment influence line at quarter point of mid-span

图10 中墩墩底弯矩影响线Fig.10 Moment influence line at bottom section of central pier

在此以该连续刚构桥为例，将边墩与中墩分别沿竖向长度4 等分，等分处截面自墩顶至墩底分别编号1～5(位移效应由于墩底位移恒为0，故无5 号点)。分别将以上各截面位置的位移、弯矩影响线转换为车辆以单位速度过桥时的荷载效应时程曲线并对其进行傅里叶变换求得基频，将结果进行整理后如图11 所示。

由图11 可以看出：中墩各位置荷载效应基频分布较整齐，边墩各位置荷载效应基频分布较零散，但两者均处于图示范围内。不难得出，当桥梁中跨跨径为L，车辆行驶速度为v 时，其对于主墩各截面的荷载激扰基频范围fv为

当荷载激扰基频fv与桥墩基频fb接近时结构会产生较明显的共振效应。当fb已知时，结合式(9)，即可得偏保守的单车辆车桥耦合共振判定公式：

其中：fb为桥墩基频；k 为安全系数。当单车辆行驶速度满足式(10)所示范围时，结构存在车桥耦合共振的可能性；反之，则认为无法产生车桥耦合共振效应。为便于广大工程师使用，可将k 近似取为1.3，得到行驶车速的“不安全”范围为

图11 桥墩各位置荷载效应基频分布Fig.11 Distribution of basic frequency at each section of piers

根据式(11)可判定单车辆匀速行驶时发生车桥耦合共振的可能性。当车桥发生共振时，荷载效应随时间迅速增大。由于单车辆自身荷载效应较小，且受桥梁全长与行车速度的限制，共振时间(即行驶车辆位于桥面的时间)较短，故单车辆共振效应较弱，对结构安全性影响较小，但结构动态响应与静态响应有明显的差异，动力放大系数显著增大。

2.3 多车辆车桥耦合共振判定方法

对于多车辆组成的车流荷载，不同车辆与不同车间距组成的“杂乱车流”产生车桥耦合共振概率极小，为此，这里着重讨论对于车桥耦合共振效应较不利的相同车型等间距过桥工况。由于车辆为等间距布置，当车流布满于全桥时，t0时刻桥面的车辆位置与t0+t时刻的车辆位置完全一致，如图12 所示(其中，t 为车辆行驶1 个车间距所需时间)。从图12 可见：等间距车流对桥梁的荷载效应以车辆间隔时间t 为周期。车流荷载对桥梁的激扰频率fv可按下式计算：

图12 不同时刻车辆位置对比Fig.12 Comparison of vehicle position at different moments

其中：v 为车辆行驶速度；sv为相邻车辆纵向间隔距离。对于通常的高墩大跨径连续刚构桥梁，基频往往较低，当车流荷载激扰频率fv与桥墩基频fb接近时结构会产生较明显的共振效应；反之，则不会产生明显共振。

2.4 车桥耦合共振判定算例分析

以2.1 节中的桥梁与车辆模型为例，应用本文方法对不同工况下的车桥耦合振动进行分析。各工况计算参数见表2，桥梁基频及对应振型见图13，时程响应分析结果见图14～17。

工况编号本文方法判定结果1单车辆60—0.040～0.1350.189无共振2单车辆120—0.080～0.2700.189共振310 辆车等间距602.50.4000.189无共振410 辆车等间距1202.50.4000.189无共振510 辆车等间距605.00.2000.189共振610 辆车等间距1205.00.2000.189共振车辆布置形式行车速度/(km·h-1)车辆间隔时间/s荷载激扰频率fv/Hz桥梁基频fb/Hz

图13 结构一阶振型(基频fb=0.189)Fig.13 First mode shape of structure(basic frequency fb=0.189)

图14 工况1 和2 时墩顶顺桥向位移对比Fig.14 Comparison for longitudinal displacement of pier between Conditions 1 and 2

图15 工况3 和4 时墩顶顺桥向位移对比Fig.15 Comparison for longitudinal displacement of pier between Conditions 3 and 4

分析结果表明：

图16 工况5 和6 时墩顶顺桥向位移对比Fig.16 Comparison for longitudinal displacement of pier between Conditions 5 and 6

图17 120 km/h 时各工况跨中位移对比Fig.17 Comparison for displacement at mid-span in all conditions at 120 km/h

1) 连续刚构桥梁由于基频较小，可能与单车辆或等间距车流产生共振现象。采用本文提出的共振效应判定方法与算例结果较吻合。由于连续刚构桥基频对应振型主要体现在桥墩位移，主梁位移很小，故桥墩响应的共振现象十分明显，而主梁共振现象不明显。

2) 现行规范中结构的冲击系数随结构基频降低而减小，但考虑共振效应后的连续刚构桥梁(由其是桥墩动态响应)并不满足此规律。

3) 在单车辆作用下，荷载对桥梁的激扰频率主要由行驶速度与桥梁中跨跨径确定；在等间距车流作用下，激扰频率则主要由行驶车辆纵向间隔时间确定。车辆分析模型及桥面平整度对冲击系数有影响但不改变共振状态，移动车辆的自身振动频率对共振状态影响极小。

3 结论

1) 提出一种基于ANSYS 单一环境下的车桥耦合振动数值求解方法。该方法将桥梁与车辆模型独立建立在ANSYS 环境下，并将两者间耦合作用关系通过APDL 编程语言计算并将其在任意时刻施加于车辆及桥梁结构中，最终得到振动响应曲线。该方法易于操作，结果精度较高。通过与既有文献及实桥测试的结果对比，验证了本文方法的正确性，为公路复杂桥型的车桥耦合振动研究提供了一种可行的数值方法。

2) 分别提出单车辆及多车辆与连续刚构桥梁发生共振响应的判定方法，证明了连续刚构桥梁发生车桥耦合共振的可能性，并给出了具体的判定公式。对不同工况下的车桥耦合振动响应及共振状态进行了算例分析，与车桥耦合共振响应判定结果较吻合。

3) 应重视车桥耦合共振等小概率高危害事件的预防工作，建议连续刚构桥运营时在桥面各车道纵向不同位置分别设置减速标志，将车流“打乱”，减小共振概率。对于特殊状况下的车队，过桥时，尽量分散行驶于各车道，避免单车道等间距行驶从而与桥梁结构产生共振。

[1] Dahlberg T. Vehicle-bridge interaction[J]. Vehicle System Dynamics,1984,13(1):187-206.

[2] Diana G, Gheli F. Dynamic interaction of railway systems with large bridges[J]. Vehicle System Dynamics, 1989, 18(1):71-106.

[3] 李国豪. 桥梁结构稳定与振动(修订版)[M]. 北京: 中国铁道出版社,2003:51-62.LI Guohao. Stability and vibration of bridge structures[M].Beijing:Railway Publishing House of China,2003:51-62.

[4] 夏禾. 车辆与结构动力相互作用[M]. 北京: 科学出版社,2002:39-48.XIA He. Dynamic interaction of vehicles and structures[M].Beijing:Science Press,2002:39-48.

[5] 谢旭, 朱越峰, 申永刚. 大跨度钢索和CFRP 索斜拉桥车桥耦合振动研究[J]. 工程力学,2007,24(增刊I):53-61 XIE Xu, ZHU Yuefeng, SHEN Yonggang. Study on vibration of long-span cable-stayed bridge with steel and CFRP cables due to moving vehicles[J].Engineering Mechanics,2007,24(I):53-61

[6] 肖勇刚, 朱素红. 车桥耦合系统的非线性动力分析[J]. 振动与冲击,2007,26(8):104-108.XIAO Yonggang, ZHU Suhong. Dynamic analysis of vehicle-bridge coupled interaction system[J]. Journal of Vibration and Shock,2007,26(8):104-108.

[7] 叶茂, 谭平, 任珉, 等. 多个车辆荷载作用下桥梁演变随机振动分析[J]. 振动工程学报,2010,23(3):269-274.YE Mao, TAN Ping, REN Min, et al. Evolutionary random vibration analysis of a bridge subjected to moving vehicles[J].Journal of Vibration Engineering,2010,23(3):269-274.

[8] 陈榕峰. 公路桥梁车桥耦合主要影响因素仿真分析方法研究[D]. 西安: 长安大学公路学院,2007:28-46.CHEN Rongfeng. Simulation approach to the main factors of vehicle-bridge coupled vibration[D]. Xian: Chang’an University.Highway School,2007:28-46.

[9] 宋一凡. 公路桥梁动力学[M]. 北京: 人民交通出版社,2000:113-132.SONG Yifan. Highway bridge dynamics[M]. Beijing: China Communications Press,2000:113-132.

[10] 郭文华, 陈代海, 李整. 二期恒载对大跨度斜拉桥车桥耦合振动的影响[J]. 中南大学学报(自然科学版), 2011, 37(8):2423-2429.GUO Wenhua, CHEN Daihai, LI Zheng. Influence of secondary dead load on vehicle-bridge coupling vibration of long-span cable-stayed bridges[J]. Journal of Central South University(Science and Technology),2011,37(8):2423-2429.

[11] 王凌波, 马印平, 蒋培文, 等. 连续刚构体系车桥耦合振动敏感性参数研究[J]. 合肥工业大学学报(自然科学版), 2014,37(8):901-906.WANG Lingbo, MA Yinping, JIANG Peiwen, et al. Sensitive parameter analysis of vehicle-bridge coupled vibration based on continuous rigid system[J]. Journal of Hefei University of Technology,2014,37(8):901-906.

[12] 曾攀. 有限元分析及应用[M]. 北京: 清华大学出版社,2006:221-222.ZENG Pan.Finite element analysis and applications[M]. Beijing:Tsinghua University Press,2006:221-222.

[13] 张雄, 王天舒. 计算动力学[M]. 北京: 清华大学出版社,2007:259-276.ZHANG Xiong, WANG Tianshu. Computational dynamics[M].Beijing:Tsinghua University Press,2007:259-276.

[14] 王新敏.ANSYS 工程结构数值分析[M]. 北京: 人民交通出版社,2007:108-112.WANG Xinmin. ANSYS numerical analysis of engineering structures[M]. Beijing: China Communications Press, 2007:108-112.

[15] 邓凡平.ANSYS10.0 有限元分析自学手册[M]. 北京: 人民邮电出版社,2007:66-75.DENG Fanping. ANSYS10.0 finite element analysis self-study manual[M].Beijing:Post&Telecom Press,2007:66-75.

[16] 曹雪琴. 桥梁结构动力分析[M]. 北京: 中国铁道出版社,1987:139-145.CAO Xueqin. Dynamic analysis of bridge structure[M]. Beijing:Railway Publishing House of China,1987:139-145.