具有量化反馈的顾前顾后型车辆跟随控制
王鹏,张继业,宋鹏云,陈彦秋
(西南交通大学 牵引动力国家重点实验室,四川 成都,610031)
近年来,随着计算机通信与网络技术的发展,网络传输信号对控制系统的影响引起了学者们的广泛关注[1]。对于非自主车辆控制,每个车辆需要通过车队内的无线网络来传递状态信息[2],研究网络因素对车辆跟随控制器的影响是有必要的。量化误差是网络传输的一个重要因素。文献[3]首先将量化误差处理为系统状态的不确定性,针对具有量化反馈的线性系统,基于线性矩阵不等式方法设计了鲁棒控制器。文献[4]进而将该方法引入到网络传输环境下的车辆跟随系统,并设计了保性能/ H∞控制器。但是该方法是一种集中式控制器的设计方法,当车辆数较多时,求解的矩阵维数较高,计算量较大。因此,在此基础上,文献[5-6]应用包含原理对跟随误差关联系统进行解耦,对解耦的子系统设计了分布式保性能控制器,并通过收缩扩张条件将其转换回原耦合系统,降低了计算量,便于应用。然而文献[4-6]均要求得到线性化的车队模型,而车辆本身的复杂性及路况的影响常常需要通过非线性模型来进行描述。文献[7-9]建立了车辆跟随系统的非线性模型,并利用加权Lyapunov 函数法和传递函数法研究该系统的群稳定性。但是该方法只适合于弱耦合的关联系统。文献[10-11]则利用向量Lyapunov函数法分析了车辆跟随系统的群稳定性,并设计了纵向跟随滑模控制器,确保系统稳定的控制器参数条件较文献[7]得到较大改善。文献[12-13]进一步分析了随机因素和脉冲因素对群稳定性的影响,并研究相应的车辆自动跟随滑模控制律。这些系统模型均只考虑了前方车辆的信息,而没有考虑后方车辆的信息。由于车辆间的设定间隔通常较小,为了进一步确保车队的安全行驶,每个跟随车辆应同时兼顾其前后车辆的状态信息。因此,文献[14-15]在文献[10]的基础上研究了一类考虑前后车辆信息的顾前顾后型车辆跟随系统,并给出了相应的跟随控制律,但没有考虑网络量化因素对控制系统的影响。因此,本文作者针对顾前顾后的车辆跟随系统模型,研究了具有量化反馈的纵向跟随控制器,设计方法计算量小,控制参数易于满足群稳定性条件。
1 系统建模及问题描述
1.1 系统模型
考虑图1 所示自动化公路系统的车辆纵向编队,该编队采用固定间隔跟随策略,图中Li(i=1,2, …)表示第i 辆车与第i-1 辆车之间设定的固定空间间隔,xi,vi,ai,Mi(i=0,1,2, …)分别表示第i 辆车的位移、速度、加速度和质量,其中i=0 表示领头车辆。

图1 车辆纵向编队Fig.1 Longitudinal vehicles in platoon
定义车队中第i 辆车与第i-1 辆车的跟随误差

其中:t 表示时间。第i 辆车与领头车辆之间的跟随误差为

根据车辆纵向动力学模型[2],第i 个跟随车辆的纵向动力学行为可用如下非线性微分方程表示


1.2 问题描述
1.2.1 车队信息反馈结构
本文考虑无线网络量化误差在车队信息传输中的影响,车队信息反馈结构如图2 所示。

图2 车队状态信息传输结构Fig.2 Information structure of states of vehicles in platoon

1.2.2 网络通信约束
对于车队内第i 辆跟随车辆定义量化器[3]hi(⋅) ,i=1, 2, …, 每个hi(⋅)的量化级集合为

量化器函数hi(⋅)将每个变量值y 映射到Wi的一个元素,其映射关系定义为
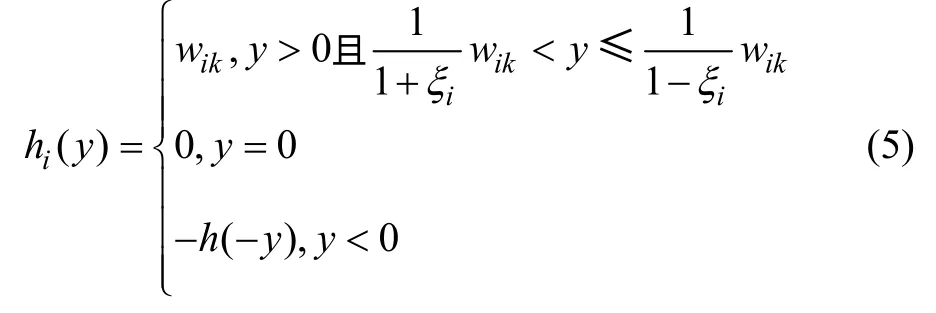
其中:ξi=(1-ρi) /(1+ρi)。
按照文献[4]的处理方式,量化误差作为系统状态的不确定性,可得如下关系

因此,考虑量化器对信息传输的影响,控制律将具有如下形式

1.2.3 控制器目标
对于每个跟随车辆,根据反馈的领头车辆和相邻前后车辆的状态信息,寻找适当的控制输入(8),满足以下要求:
1) 车辆个体稳定性:车队内每个跟随车辆的跟随误差ei(t)渐近趋于0。
2 车辆纵向跟随控制
对于自动化车辆跟随系统,车辆间的跟随误差可通过如下形式的关联系统进行描述。

其中, i∈N,yi∈Rn;fi:Rn×Rn×Rn→Rn,且fi(0,0,0)=0。假定系统(9)满足零解的存在性和唯一性条件。

引入基于向量Lyapunov 函数方法得到的关联大系统(9)的稳定性引理,作为纵向跟随控制器设计的基础。
引理1[14]对于系统(9),若满足以下条件,则其零解是群指数稳定的。
(i)∀mk,nk∈Rn,k=1,2,3,

(ii) 对于系统y˙i=fi(yi,0,0)(i=1, 2, …),存在一个Lyapunov 函数Vi(yi)和正数 αl, αh, α1, α2,使得

2.1 滑模控制器
采用滑模控制方法设计系统控制器,定义切换函数

其中: q1,q2,q3和 q4是待定参数。对 Si求导,并将式(3)代入得

为了使系统的状态满足滑动模态的可达条件,取非线性控制律


其中:sign 为符号函数;λ>0为可选控制参数。由式(12)和(13)可得第i 个跟随车辆的控制律为

2.2 稳定性分析
2.2.1 滑动模态的可达性
下面证明车辆跟随系统(3)在控制律(17)调节下的滑动模态渐近可达。取Lyapunov 函数

并令
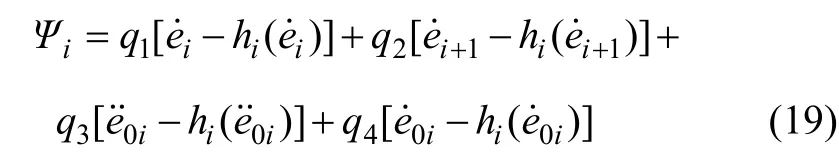
则式(18)沿式(10)对时间求导,并代入式(17)和(19)得

考虑式(6),由式(20)得

再考虑不等式(7),并代入式(14)和(15),由式(21)得

因此,系统的滑动模态是渐近可达的。
2.2.2 滑模运动的稳定性
通过确定控制参数q1,q2,q3和q4,使得t→∞时,ei( t)→0。联系式(10),由滑模面Si=0,i=1,2, …可得

因此,由式(23),ei(t)的滑模运动方程为


可见:式(25)与式(9)的形式是一致的。
定理1 对于系统(25),若满足

则系统(25)的零解是群指数稳定的。
证明 由式(26)可知,q1,q3,q4同号,并且q2与q1,q3,q4异号,因此

容易验证∀mk,nk∈R,k=1, 2, 3

即满足引理1 的条件(i)。取Vi= ei2,则可取αl=1,αh=1,α1=2l1,α2=2,满足引理1 的条件(ii);又由于q4/q3>0,可得l2+l3<l1,因此

满足引理1 的条件(iii)。所以根据引理1,若系统(25)满足条件(26),则零解是群指数稳定的。证毕。
3 仿真分析
设车队由1 辆领头车辆和4 辆跟随车辆组成,设置量化密度ρi=0.6,按照文献[15]设车辆质量均为1 000 kg,受到的摩擦力为200 N,空气阻力系数为0.5 N·s2/m2,车间固定间隔为12 m;初始位移为x0(0)=100.0 m,x1(0)=90.0 m,x2(0)=79.5 m,x3(0)=68.5 m,x4(0)=57.0 m,即初始车辆间距误差e1(0)=2.0 m,e2(0)=1.5 m,e3(0)=1.0 m,e4(0)=0.5 m;初始速度设为v0(0)=25.0 m/s ,v1(0)=24.5 m/s ,v2(0)=24.0 m/s ,v3(0)=23.5 m/s,v4(0)=23 m/s;初始加速度a1,a2,a3,a4均为0 m/s2,领头车辆加速度的变化如下

控制律采用式(17),控制参数分别取q1=0.3,q2=-0.3,q3=0.3,q4=0.3,λ=0.2。容易验证q1,q2,q3和q4的设置满足定理1 的稳定条件。为了削弱控制输入的颤振,将控制项(13)中的符号函数改为饱和函数

其中:

采用此种控制律虽然不能保证Si→0,但是能实现其一致最终有界。取Φi=0.2,i=1,2, …,仿真结果如图3 和图4 所示。
由图3(a)可以看出:车辆之间保持着固定间隔,而图3(b)和(c)则显示车队内四辆跟随车辆的速度和加速度能够很快的逼近领头车辆的速度和加速度。由图4 可知:所有车辆的跟随误差在12 s 内均已收敛到0,实现了车辆固定间距纵向跟随的自动跟随行驶策略。
图5 给出了第4 辆跟随车辆的跟随误差信息量化的结果,车辆跟随误差的真实值经过对数量化器传输变成了一个离散量化值的集合。在控制器设计阶段,应该考虑对网络传输量化误差进行补偿,否则控制器的性能将因为信息传输的不准确而受到影响。
在不考虑车辆间信息传输的量化误差,其余系统参数不变的情况下,按文献[14]取控制律

与本文设计的控制器进行比较。跟随误差的仿真结果见图6。
由图6 可知:4 辆跟随车辆的跟随误差在接近40 s时才收敛到0。与图5 对比可知:由于本文设计的控制律考虑了量化误差的影响,车辆跟随误差具有更快的收敛速度。
为了进一步验证本算法的有效性,在之前算例的基础上,即车队所有车辆已保持10 m 间隔,并且以25 m/s 的速度在路上行驶时,领头车辆突然在2 s 时间内实现紧急制动并减速到0 m/s,其余跟随车辆的仿真计算结果如图7 所示。
由图7(a)可知:所有跟随车辆均在2 s 时间内实现了制动,并减速到0 m/s。而图7(b)则显示车辆间的跟随误差也基本保持为0,没有发生剧烈变化,避免了安全事故的发生。

图3 车队车辆状态Fig.3 States of vehicles in platoon
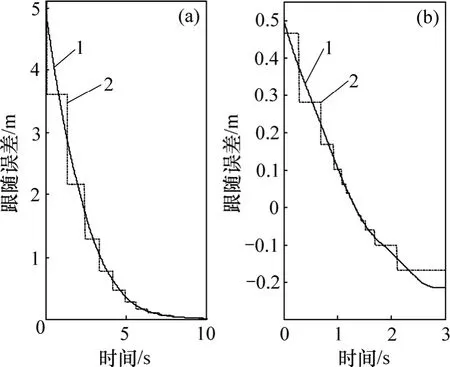
图5 第4 辆跟随车辆接收的跟随误差Fig.5 Following displacement errors received by the 4th following vehicle

图6 未考虑量化误差时的跟随误差Fig.6 Following displacement errors without quantized error compensation

图7 车队车辆紧急制动Fig.7 Emergency breaking for vehicles in platoon
4 结论
1) 基于车辆非线性纵向动力学模型,采用固定距离跟随策略,得到了对数量化器传输信道下的顾前顾后型车辆跟随系统数学模型。
2) 将量化误差处理为系统不确定性,应用向量Lyapunov 函数法得出的关联大系统群指数稳定性判据,研究了补偿量化误差的自动车辆跟随系统的滑模控制器设计。该控制器是一种分布式控制器,计算量小,控制参数易于满足群稳定性条件。
3) 与不考虑量化误差的控制方法相比,应用本方法的车辆跟随系统,其跟随误差能够更快地收敛到0。
[1] Lubomir B, Martin P. Decentralized control and communication[J]. Annual Reviews in Control, 2012, 36(1):1-10.
[2] Rajesh R.Vehicle dynamics and control[M].New York:Springer,2006:187-220.
[3] Fu M Y, Xie L H. The sector bound approach to quantized feedback control[J]. IEEE Transactions on Automatic Control,2005,50(11):1698-1711.
[4] Guo G, Wei Y. Hierarchical platoon control with heterogeneous information feedback[J]. IET Control Theory and Application,2011,5(15):1766-1781.
[5] 岳伟, 郭戈. 通讯网络影响下自主车队的控制[J]. 控制理论与应用,2011,28(7):1041-1048.YUE Wei, GUO Ge. Control of autonomous platoon under networked communication effect[J]. Control Theory &Application,2011,28(7):1041-1048.
[6] 岳伟, 郭戈. 通信网络影响下的自主车队分散式控制[J]. 东南大学学报(自然科学版),2011,41(S1):144-151.YUE Wei, GUO Ge. Decentralized control of autonomous platoon under networked communication effect[J]. Journal of Southeast University (Natural Science Edition), 2011, 41(S1):144-151.
[7] Swaroop D, Hedrick J K. String stability of interconnected systems[J]. IEEE Transaction Automatic Control, 1996, 41(3):349-357.
[8] Swaroop D, Hedrick J K, Choi S B.Direct adaptive longitudinal control of vehicle platoons[J]. IEEE Transactions on Vehicular Technology,2001,50(1):150-161.
[9] Eyre J, Yanakie D, Kanellakopoulos I. A simplified framework for string stability analysis of automated vehicle[J]. Vehicle System Dynamics,1998,30(5):375-405
[10] Zhang J Y, Yang Y R, Zheng J. String stability of infinite interconnected system[J]. Applied Mathematics and Mechanics,2000,21(7):791-796
[11] Zhang J Y, Suda Y, Iwasa T.Vector Liapunov function approach to longitudinal control of vehicles in a platoon[J]. JSME International Journal,2004,47(2):653-658.
[12] 施继忠, 张继业, 徐晓惠. 时滞随机关联系统的群稳定性[J].自动化学报,2010,36(12):1744-1751.SHI Jizhong, ZHANG Jiye, XU Xiaohui. String stability of stochastic interconnected systems with time delays[J]. Acta Automatic Sinica,2010,36(12):1744-1751.
[13] 徐晓惠, 张继业, 张克跃. 脉冲变时滞车辆纵向跟随系统的群指数稳定性与控制[J]. 控制与决策,2012,27(9):1293-1300.XU Xiaohui, ZHANG Jiye, ZHANG Keyue. Exponential stability and control of vehicle longitudinal following system with impulsive effects and time-varying delays[J]. Control and Decision,2012 27(9):1293-1300.
[14] 任殿波, 张京明, 崔胜民, 等. 基于向量Lyapunov 函数方法的顾前顾后型车辆跟随控制[J]. 中南大学学报(自然科学版),2010,41(6):2195-2200.REN Dianbo, ZHANG Jingming, CUI Shengmin, et al. Vehicle following control using front and back information based on vector Lyapunov function[J].Journal of Central South University(Science and Technology),2010,41(6):2195-2200.
[15] 任殿波, 张策, 张继业. 考虑前后信息的车辆跟随自适应控制[J]. 哈尔滨工业大学学报,2011,43(6):76-80.REN Dianbo, ZHANG Ce, ZHANG Jiye. Vehicle following adaptive control using front and back information[J]. Journal of Harbin Institute of Technology,2011,43(6):76-80.

