临界雷诺数区准椭圆形覆冰导线风压特性研究

马文勇,张晓斌,李玲芝,刘庆宽

(石家庄铁道大学 风工程研究中心,石家庄 050043)

0 引 言

覆冰导线舞动对输电线路安全危害很大，目前仍未很好地解决。覆冰导线的气动力特性尤其是驰振气动力特性及驰振机理还不清晰是影响该问题解决的最主要因素之一。

类似于准椭圆形(又称新月形)、扇形等覆冰形状在实际导线覆冰中多次出现，因此准椭圆形及扇形断面的气动力特性及驰振稳定性受到了广泛的关注。

从研究方法上看，采用高频天平测力试验是最常用的气动力测试方法之一，通过节段模型试验，该方法可以得到近似的二维3分量气动力系数，但是该方法无法得到气动力沿覆冰导线截面周向的分布情况，也无法反映导线轴向不同位置气动力的相关性。

影响类似于覆冰导线截面形状气动力的因素很多，雷诺数、表面粗糙度和来流湍流度是最重要的3个影响因素，这些因素对气动力的影响规律仍没有定论。其中临界雷诺数区内气动力特性是研究的重点和难点之一，一般认为，输电导线由于其直径较小(钢芯铝绞线直径一般小于5cm)，其雷诺数很难达到临界区，但在冻雨等条件下，覆冰往往可以达到几倍的导线直径。另外湍流度和表面粗糙度的影响也可以减小临界区的起始雷诺数。

圆形截面在临界雷诺数范围阻力系数下降同时产生不对称的平均升力系数[1]，这种力系数随雷诺数的变化被用于解释干索驰振现象[2]及其它振动现象[3-4]，而临界雷诺数范围内圆形截面的驰振不稳定性[5]与椭圆形截面的驰振不稳定性[6]也受到了研究者的重视。类似于本文所研究的准椭圆形断面在临界区的气动力特性仍未见报道。

本研究通过刚性模型测压试验，得到不同雷诺数下准椭圆形覆冰导线风压分布，讨论亚临界区风压分布与临界区的差别，分析临界区风荷载特点对覆冰导线驰振的影响。试验结果有效补充高频天平测力的结果，为进一步研究三维导线气动力模型、覆冰导线非定常特性和驰振机理的参数分析提供研究基础。

1 研究概况

1.1试验模型

利用刚性模型进行测压试验，模型采用ABS板制作，表面均匀喷涂微粒直径小于1×10-5m的油漆，中间固定钢管以保证其刚度。其中试验模型概况如图 1所示。模拟导线直径为D，覆冰厚度Di为0.25D。

为了提高测试信号的信噪比同时考虑到方便测压孔的布置，导线模型直径约为LGJ-800/100型钢芯铝绞线(LGJGB117983)外径的2.5倍，即D=100mm。试验中采用端板消除端部效应的影响，模型长度为L=2m，端板为直径550mm的圆板。长度与直径比为20。

(a) 安装在风洞中的模型

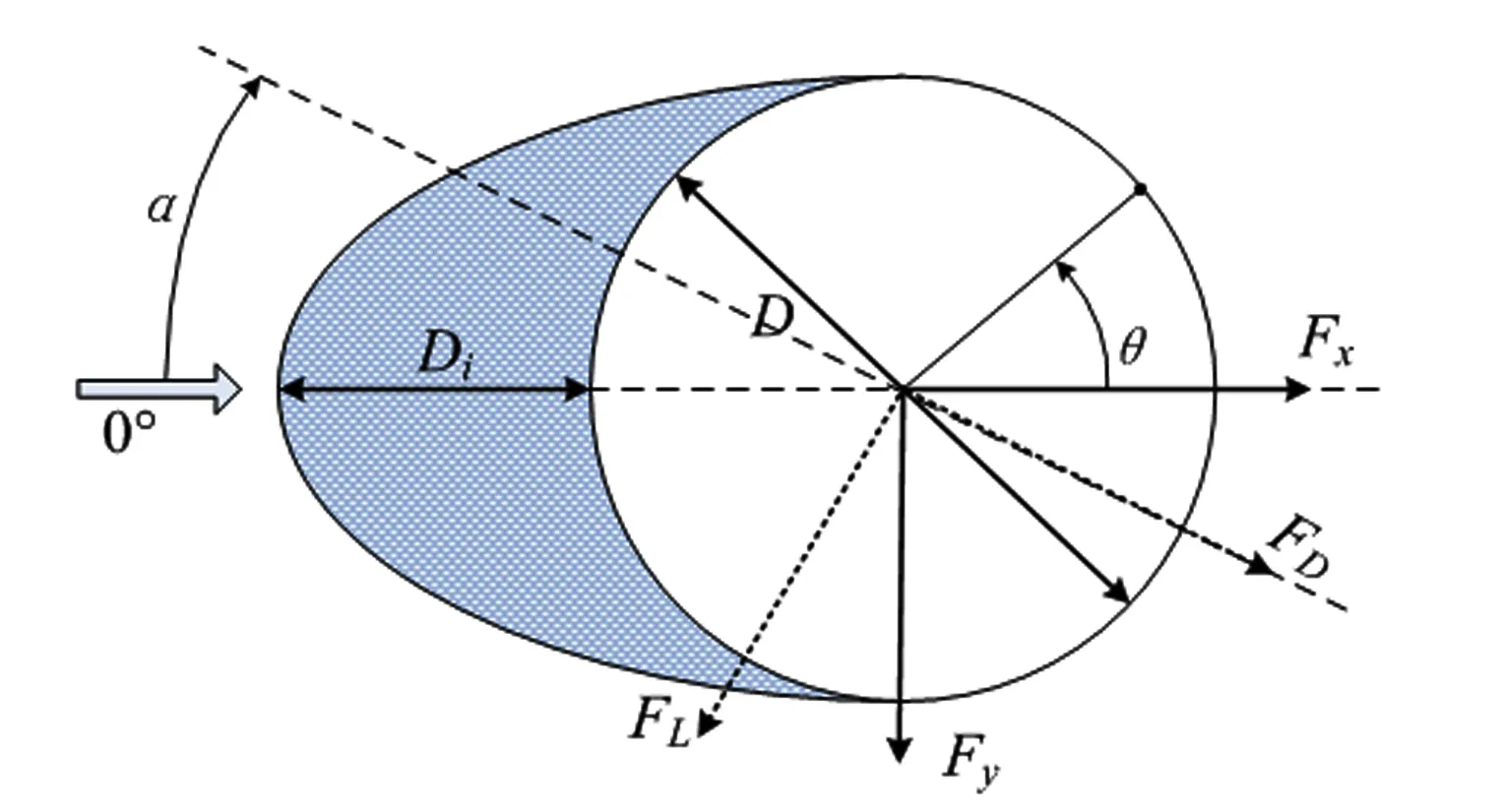
(b) 模型及试验工况

1.2来流条件及试验工况

试验在石家庄铁道大学STU-1风洞试验室高速段内进行[7]，流场为近似均匀层流，来流平均风速U分别为5m/s、7.5m/s、10m/s、15m/s和20m/s，对应的背景湍流度在0.2％～0.5％之间。试验风向角为α，测试范围0°～180°，间隔5°。

采用刚性模型进行测压试验，测压管内径0.9mm，最长测压管长度为500mm，并采用分布摩擦模型对测压管路信号进行修正[8]。由于临界雷诺数区风荷载对结构表面及形状很敏感，为了防止单个截面气动力的随机性，试验中沿模型轴向共在四个截面上布置测压孔，依次为S1、S2、S3、S4，其间距分别为D、3D、2D；测压孔沿截面周向位置方位用θ表示，模型沿周向共布置50个测压孔。

1.3参数定义

采用风压系数描述表面风荷载的分布定义为

(1)

其中：pi为测点测试风压；p0为环境静压；ρ为空气密度；U为来流风速。风压系数Cp(t)的平均值用Cp表示，均方根值用Cpr表示，分别称为平均风压系数和脉动风压系数。

阻力系数和升力系数定义为：

(2)

其中：FD(t)和FL(t)分别为风轴坐标系下的阻力和升力；CD(t)和CL(t)为升力系数和阻力系数，其平均值和均方根值分别用CD、CL和CDr、CLr表示，称为平均阻力、升力系数和脉动阻力、升力系数。

雷诺数Re计算采用直径D作为特征长度，试验雷诺数范围从Re=3.45×104(U=5m/s)到Re=13.8×104(U=20m/s)，最大雷诺数对应输电导线承受的真实风速大于50m/s。

在10m/s风速下对模型及风场的对称性进行测试，图 2为测试结果，模型及风场的对称性良好，迎风向测点风压系数值接近1.0，表明来流风速测量准确，无量纲风压系数计算准确。

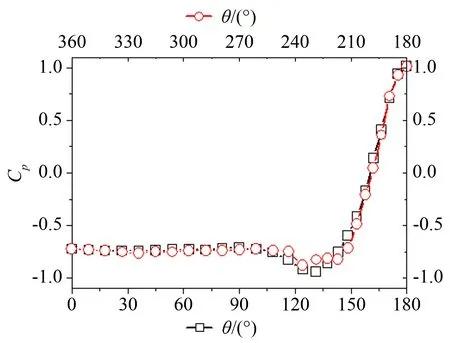
图2 对称性测试

2 风压分布结果分析

2.1平均气动力分析

图3给出了不同雷诺数下覆冰导线的平均阻力系数。当Re=13.8×104时，各个风向角下的阻力系数明显小于Re<10×104对应值，这是临界雷诺数区域阻力系数的一个明显特征。对应的平均升力系数如图4所示，图中在某些风向角下(30°风向角左右)，平均升力系数与亚临界区的对应值差别较大。

图3 平均阻力系数

图4 平均升力系数

为进一步说明图4中平均升力系数的差别，图5给出了不同测试截面临界雷诺数下的平均升力系数。

图3～5说明，对于该准椭圆形覆冰导线，当雷诺数在(3.5～10)×104之间，平均阻力系数和升力系数不随雷诺数变化，当雷诺数达到13.8×104时，平均力系数与雷诺数在10×104以下的对应值差别较大。这种力系数随雷诺数的变化对来流条件和表面粗糙度等参数很敏感，图5中4个截面并未同步发生该现象：S2截面在0°～40°风向角下，S3和S4截面在150°～180°风向角下并未发生明显的变化。文献[1,3,9]等均发现在特定雷诺数下圆形等对称结构会产生不对称的平均升力，图5中S1和S2截面在180°角下也发现了类似的现象，这种现象可能是由于特定雷诺数下(一般在临界区)结构表面流体分离对流场及结构表面条件等特别敏感所造成的。由于试验条件非理想化，因此该现象有一定的随机性。在本文的验证试验中，这种随机现象也得到了体现，即在不同批次的试验中，平均升力的方向及发生的截面会发生变化。

图5 不同截面平均升力系数

依据图5中平均升力系数随风向角的变化，选取图6中0°、30°、170°和180°风向角下，Re=13.8×104和Re=6.9×104平均风压系数的分布。

Re=6.9×104时，平均风压系数分布随风向角变化比较平缓，而Re=13.8×104时，随着风向角的变化，平均风压系数分布形式变化剧烈，如170°和180°风向角下风压系数分布差别明显，且在180°风向角下产生不对称的风压分布。

30°风向角下，2个雷诺数下的平均风压系数分布形态接近，但在高雷诺数下来流两侧的风压差异更大，这说明，2种雷诺数下来流两侧流体分离特点有较大的差异。

2.2脉动气动力分析

图7和8分别为不同雷诺数下的阻力系数均方根和升力系数均方根值。

Re=13.8×104的升力系数均方根值在110°～170°风向角下明显小于其它雷诺数下的对应值。图9为2种雷诺数及不同风向角下的风压系数均方根分布。

图6 平均风压系数分布

图7 阻力系数均方根值

图8 升力系数均方根

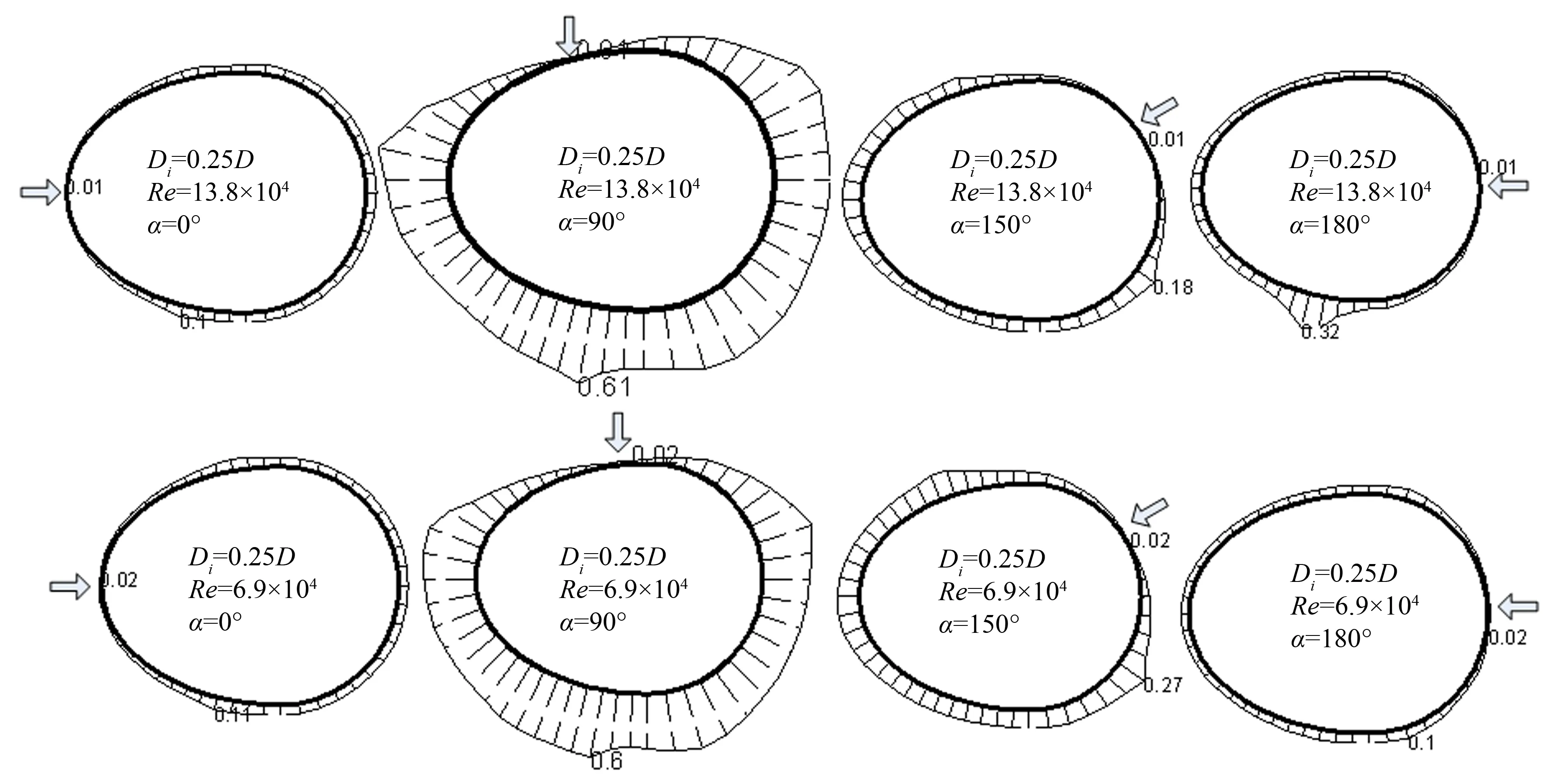
图9 风压系数均方根分布

图中0°和90°风向角下，2个雷诺数的脉动风压系数分布及值都比较接近，而150°的脉动风压系数值差别大，180°风向角下雷诺数为13.8×104时，局部脉动风压系数较大。

2.3风力谱及风压相关性分析

当雷诺数小于10×104时，准椭圆形覆冰导线在不同的风向角下的升力系数功率谱为单峰功率谱，其对应的斯托罗哈数如表1所示。其中f为频率，单位为Hz,Re=6.9×104。

表1 斯托罗哈数

图10为2种雷诺数下的升力系数功率谱，其中SCL为升力系数功率谱。当雷诺数为6.9×104时，各个风向角下的功率谱图为单峰功率谱，说明此时的漩涡脱落频率有规律，而当雷诺数为13.8×104时，部分风向角下的功率谱并不存在峰值，说明其不存在规则的漩涡脱落。这种漩涡脱落形式的差别，也是雷诺数效应的一个典型特征。

图11给出了2种雷诺数下S1截面周向测点与来流正对测点的风压系数相关系数。

从图11可以看出，2种雷诺数下，风压的周向相关性类似，其中雷诺数为6.9×104时，其周向相关性更强一些。

图10 升力系数功率谱

3 雷诺数对驰振稳定性的影响

Den Hartog横风向驰振机理认为，产生驰振不稳定的必要条件是升力系数随风向角增大而减小，其数学表达式为：

(3)

从平均气动力分析的结论可以看出，当雷诺数增大为13.8×104时，升力系数随着风向角变化下降更迅速，发生横风向驰振的可能性增大。

考虑到导线迎风向覆冰的特点，图12给出了0°～90°风向角下S1截面2种雷诺数的下的平均升力系数和阻力系数并分析其横风向驰振的Den Hartog系数(见图13)，可以看出，雷诺数为13.8×104时，更容易发生横风向驰振。

上述雷诺数对驰振气动稳定性产生影响的对应风速为40m/s以上，而实际常发生覆冰导线舞动的风速一般在20m/s以下。但是依据圆形截面的雷诺数研究成果，表面粗糙程度和湍流度的增强会使临界区提前。因此，雷诺数效应可能是引起实际覆冰导线舞动的主要原因，至少该因素应作为覆冰导线舞动分析中重要的影响因素。

图13 Den Hartog系数

4 结 论

针对本研究的准椭圆形覆冰导线，当雷诺数达到临界区，与亚临界区的对应值相比，平均阻力系数下降、平均升力系数变化剧烈且在某些对称风向角下产生横风向平均升力系数，平均风压系数分布对风向角等参数更为敏感；旋涡脱落由亚临界区的规则脱落变为不规则脱落，周向相关性减弱，特征频率消失；临界区内平均升力系数随风向角变化的快速下降使得结构更易满足横风向驰振判别准则。

参考文献:

[1]Zdravkovich M M.Flow around circular cylinder[M].New York: Oxford University Press,1997.

[2]Matsumoto M,Yagi T,Hatsuda H,et al.Dry galloping characteristics and its mechanism of inclined/yawed cables[J].Journal of Wind Engineering and Industrial Aerodynamics,2010,98(6-7): 317-327.

[3]刘庆宽,张峰,马文勇,等.斜拉索雷诺数效应与风致振动的试验研究[J].振动与冲击,2011,30(12): 114-119.

Liu Qingkuan,Zhang Feng,Ma Wenyong,et al.Tests for Reynolds number effect and wind-induced vibration of stay cables[J].Journal of Vibration and Shock,2011,30(12): 114-119.

[4]马文勇,顾明,全涌,等.覆冰导线任意方向驰振分析方法[J].同济大学学报(自然科学版),2010,38(1): 130-134.

Ma Wenyong,Gu Ming,Quan Yong,et al.Analysis Method of Galloping in Arbitrary Directions of Iced Conductors[J].Journal of Tongji University(Natural Science),2010,38(1): 130-134.

[5]Nikitas N,Macdonald J H G,Jakobsen J B,et al.Critical Reynolds number and galloping instabilities: experiments on circular cylinders[J].Exp Fluids,2012(52): 1295-1306.

[6]Alonso G,Meseguer J,Sanz-Andrés A,et al.On the galloping instability of two-dimensional bodies having elliptical cross-sections[J].Journal of Wind Engineering and Industrial Aerodynamics,2010,98(8-9): 438-448.

[7]刘庆宽.多功能大气边界层风洞的设计与建设[J].实验流体力学,2010,25(3): 66-71.

Liu Qingkuan.Aerodynamic and structure desigh of multifunction boundary-layer wind tunnel [J].Journal of Experiments in Fluid Mechanics,2010,25(3): 66-71.

[8]马文勇,刘庆宽,刘小兵,等.风洞试验中测压管路信号畸变及修正研究[J].实验流体力学,2013,27(4): 71-77.

Ma Wenyong,Liu Qingkuan,Liu Xiaobing,et al.Study on correction and distortion effects caused by tubing systems of pressure measurements in wind tunnel[J].Journal of Experiments in Fluid Mechanics,2013,27(4): 71-77.

[9]刘庆宽,郑云飞,马文勇,等.雷诺数效应对斜拉索气动特性的影响[J].工程力学,2013,30(Suppl): 284-289.

Liu Qingkuan,Zhang Yunfei,Ma Wenyong,et al.Reynolds number effect on aerodynamic characteristics of stay-cables[J].Engineering Mechanics,2013,30(suppl): 284-289.

作者简介:

马文勇(1981-)，男，陕西蒲城人，博士，副教授。研究方向：结构风荷载及风致振动研究。通信地址：石家庄市北二环东路17号石家庄铁道大学风工程研究中心(050043)。E-mail：mawenyong@126.com