阵风环境模拟用控制器设计与实验研究

孟庆龙，王元，李彦鹏

1.长安大学环境科学与工程学院，西安710054

2.西安交通大学能源与动力工程学院，西安710049

1 引言

模拟包括数值模拟和物理模拟，其中物理模拟是把对实际现象的研究转换为在专门实验室条件下对缩尺或放大模型所进行的相似现象研究（一种特殊的模拟是在原型上进行，称为复现模拟）。物理模拟的基本思想，是根据模型实验的结果就能给出关于效应特性和与实际条件下的现象有关的各种量的必要的答案[1]。这种模拟是以物理实验平台为基础的。

环境模拟技术在不断解决环境模拟和实验的研究过程中，形成了独立的理论体系，其整个发展历程与环境模拟设备息息相关。环境模拟设备与实验技术经历了由静态到动态，从单参数到多参数，从产品环境到人机环境的发展过程。目前其发展方向是建立多参数综合动态环境模拟系统并进行多参数综合动态人机系统环境实验[1]。1949年美国温特教授在加利福尼亚州的帕萨迪纳主持建造了世界上首个环境模拟设施，命名为“phytotron”[2]。这个环境模拟设施的出现对当时的生物科学研究起到了极其重要的推动作用。随后，环境模拟设施如雨后春笋，广泛应用于航空、航天、海洋、农业、环境等各个领域，多种不同规模和类型的环境模拟设施相继建立[3-6]。世界上建成的最具代表性的动态综合环境模拟设施是建立在美国亚利桑那州的生物圈2号（Biosphere 2）[7]。按照设计思想，地球被称为生物圈一号，生物圈2号是地球的缩影。

实际上，成功的环境模拟必须依靠一个可靠的控制系统来维持。通过对模拟装置的改进，采用合理有效的控制技术，不但能够模拟平均风速廓线，提高气流分布均匀性，还能够模拟温度层结和太阳辐射等环境参数，更真实地反映近地层环境的实际状况，为应用研究提供可靠、可控的实验平台。因此，要在环境模拟实验室这样封闭的环境空间内实现近地层环境参数的动态模拟，就必须对环控设备进行控制。模拟是目标，控制是手段，可以这样说，缺少自动化系统的环境模拟几乎不可能实现。

本文的主要目的就是在充分了解近地层风环境特性的基础上，使用人工方法实现近地层微气候风环境模拟。通过设计合理的控制策略和先进的控制算法，提高风环境模拟精度。

2 控制对象简介-环境模拟实验室

环境模拟实验室建筑面积约105m2，屋面平均高度4.8m，局部为二层。整个实验室按空间位置分成三部分：实验区、设备室及观察控制室，其立体结构示意图如图1所示。图2给出了实验室的上部平面示意图。为构造真实近地层的局部地表环境，实验中心位置处设有6 280（L）×5 040（W）×1 350（D）的地表构造坑。实验区上部设置高度可调的全光谱日光模拟器，为将光源发出的热量排出室外，模拟器配备了通风降温系统；观察控制室设在局部二层上（下部为设备室，放置压缩机、表冷器等），实验人员通过双层玻璃窗可对实验区实验情况进行实时观测。

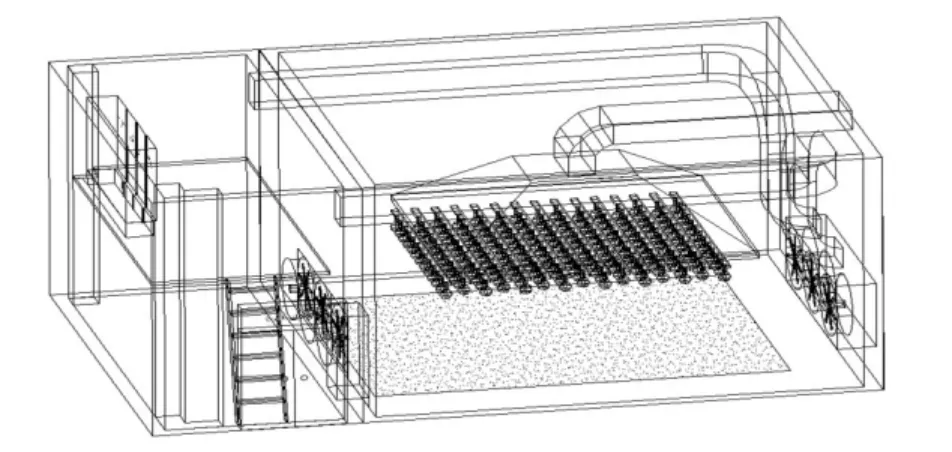
图1 环境模拟实验室立体结构示意图

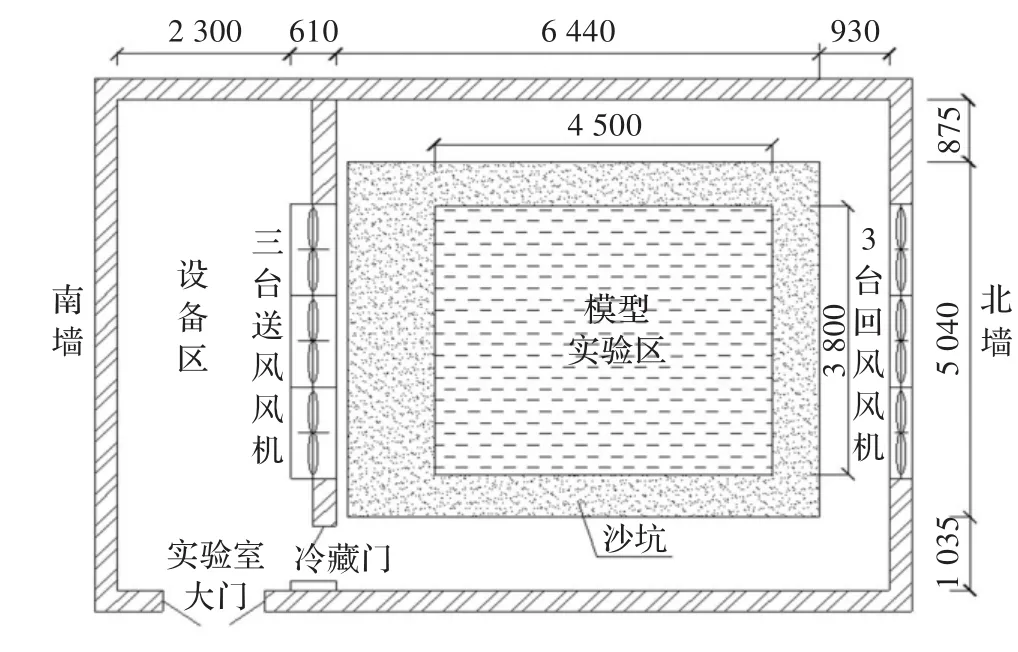
图2 环境模拟实验室下部平面图（单位：mm）

实验室内采用6台风机来模拟自然环境风。3台低噪声轴流风机作为送风机布置在实验室南侧；3台低噪声轴流风机作为回风机布置在北侧。回风管从回风风机后的静压箱伸出，沿屋顶下侧穿过实验室连接至送风风机的静压箱，形成闭式回路。风机是制造自然风的设备，为得到期望的效果，对其的精确控制非常关键。对送风机和回风机分别用两台变频器驱动，通过计算机可自动调节变频器频率来实现风速的自动控制，完成所需自然风效果的模拟。为使风机出口风速进一步提高，在送风机出口设置一收缩段。收缩段的顶面和底面不收缩，两个侧面按照维托辛斯基收缩曲线设计。为改善实验区气流特性和形成期望的风速廓线，采取增设单层或多层不等高的阻尼网，通过合理布置阻尼网的高度和层数，使模型实验区风场展向均匀且垂向满足期望得到的风速廓线[8]。考虑阵风的正弦叠加性，在满足风速廓线的同时，需要满足阵风特性，能够实现任意正弦风速的模拟。

3 控制算法：基于ILC的自校正PID控制器

迭代学习控制（Iterative Learning Control，ILC）是A rimoto在1984年针对机器人系统特点，模拟人类学习技能过程提出的[9]。它利用系统前期的运行信息，通过迭代的方式修正当前的控制信号，使系统的输出能够精确地跟踪期望轨迹。ILC最大的特点是跟踪性能会随迭代逐步改善。迭代学习控制和PID（Proportional Integral Derivative）控制一样具有简单的形式，但却不依赖系统模型。随着迭代学习控制理论的不断发展和完善，迭代学习控制方法在实际控制工程问题中也得到了广泛的应用，例如：过程工业中的批处理过程，半导体晶片的温度控制，磁盘驱动，无缝钢管壁厚控制，烟叶发酵系统等，但多局限于仿真研究[10]。虽然迭代学习控制的性能分析是建立在严格数学分析基础上的，但却不需要精确的数学模型，因而，它是简单实用的控制方法，这也是它引起人们关注的主要原因。

3.1 离散时间PID型ILC算法

假设离散时间系统的受控对象模型为：

输出误差定义为：

ek(t)=yd(t)-yk(t)

根据误差定义可以分别定义出开环和闭环PID型学习律：

比较开环控制和闭环控制两种控制策略，开环控制利用上一步的控制误差信息计算控制规律，闭环控制采用的是由上一步的控制和当前误差信息计算控制规律的方法[11-13]。考虑开环迭代学习利用信息的简单特点，本文采用开环迭代学习控制。

3.2 基于ILC的自校正PID控制器

实际应用中，系统下一次运行的新的控制既可以在上一次运行结束后离线计算得到，也可以在上一次运行中在线计算得到；新的控制量存入存储器，刷新旧控制量。在控制过程中，从存储器取出控制量。可以看出，迭代学习控制算法可利用的信息要多于常规的反馈控制算法。

如果设定值是连续变化的曲线，实际上并不会直接将设定值直接加到系统上，而是分段加到系统上。而这种分段又会引起实际值的超调，造成调节时间过长等问题[14]。为了克服这些问题，在自校正PID基础上加入ILC设定值优化序列，其控制结构如图3所示。该结构是在文献[15]基础上引进自校正控制后的改进。迭代学习的输出r为经过优化的设定值，将作为直接控制单元的设定；直接控制单元由自校正PID控制器和被控对象组成的闭环系统，系统可实时更新PID参数。实质上，迭代学习和直接控制单元构成了双闭环控制系统。内环进行系统动态控制，外环在原来阶跃设定基础上通过迭代学习进行系统设定值序列的优化调整，得到了“受控”的设定值。

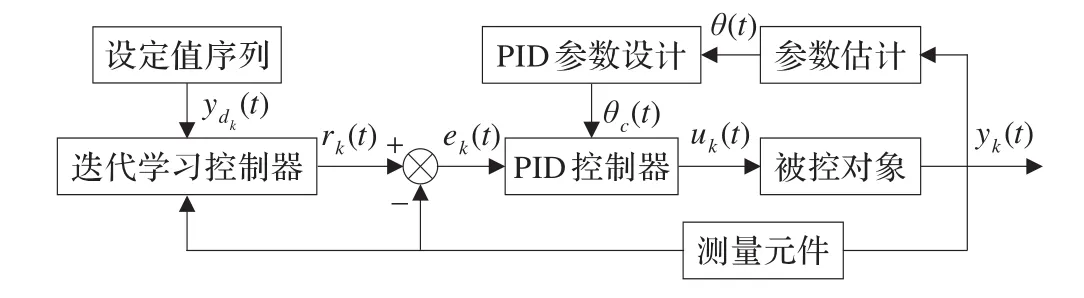
图3 基于迭代学习控制的自校正PID控制系统结构图

每个设定值下的期望轨迹定义为设ck为系统第k个的设定值，则第k个优化周期内系统的运行期望轨迹为：

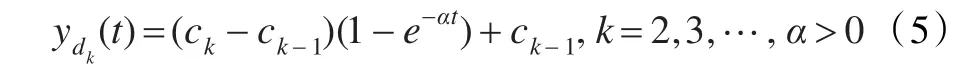
式中，α取值不同，轨迹变化快慢不同：当1＞α＞0时，期望轨迹平滑，变化缓慢。α＞1时，期望轨迹坡度大，变化迅速。

当t=0时，ydk(t)=ck-1；当t→∞ 时，ydk(t)=ck，即系统最终稳定运行于当前优化周期内的设定值ck。由上述分析可以看出，理想轨迹是第k个设定值与第k-1个设定值的差和第k-1个设定值ck-1的函数。即本次期望轨迹是在上次设定值的基础上按设定值增量的指数规律变化。

采用PD型ILC算法：

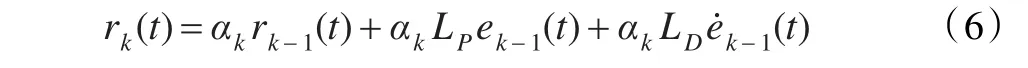
其中

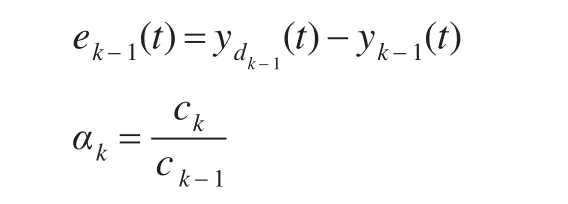
式中rk(t)为迭代学习输出的设定值；LP和LD分别为比例学习增益和微分学习增益。

将设定值序列分段加到系统上，本次迭代控制会将上次迭代学习的经验继承下来，指导本次控制量（这里为设定值rk(t)），随着迭代次数的增加，系统从一个稳态过程到另一个稳态过程实现了平滑过渡。该控制算法的流程图如图4所示。

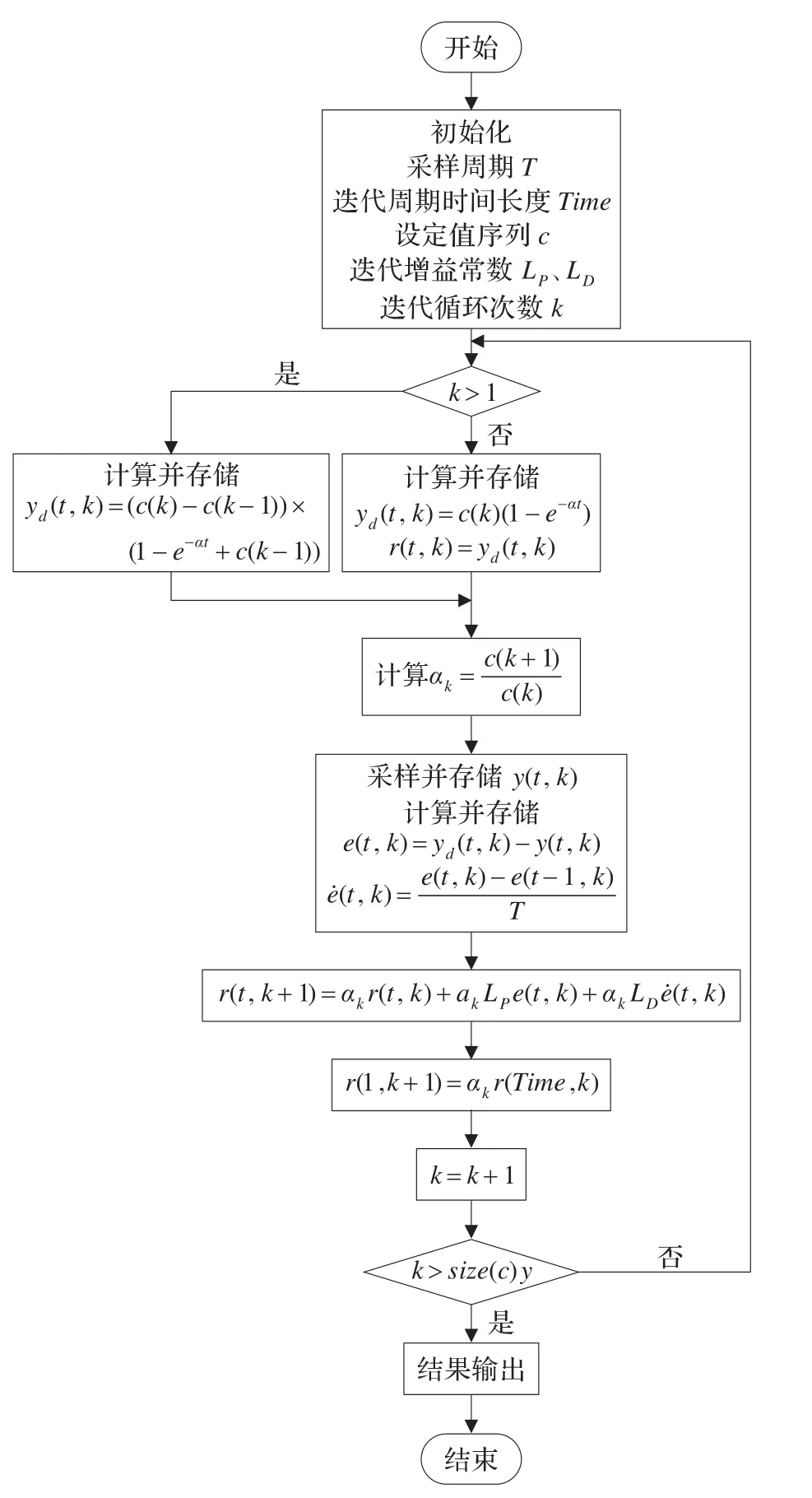
图4 基于ILC的自校正PID控制算法流程图

3.3 仿真实例

为验证该算法的有效性，对该算法进行了M atlab仿真研究。仿真模型为：

将正弦变化的设定值分为63段加到系统上，形成63个设定值序列。每个迭代周期为30 s，α取为1，LP、LD为本学习律的学习增益，为保证迭代收敛性，同时考虑收敛的快速性，通过仿真实验，LD和LP分别取为3.5和0.8。算法仿真结果如图5所示。由图可以看出，经过两次迭代学习系统的超调明显减小，随着迭代次数的增加，实际值基本上实现了期望值的无差跟踪。可以看出，随着迭代次数的增加，最大偏差很快减小，到第10次几乎达到零偏差。

图5 基于迭代学习控制的自校正控制系统仿真结果图

4 风环境模拟控制器设计

为模拟自然阵风，采用了变频技术控制送、回风机。进行阵风模拟时，采用被动和主动两种控制方式，为在模型实验区实现整场近地层风速廓线的模拟，通过合理布置阻尼网高度和层数以及粗糙元的来实现风速在垂向的廓线要求；通过设置出口收缩段和阻尼网来保证展向风速分布均匀；通过送风机和回风机的协调控制，以保证实验区纵向（风机轴向）速度分布的均匀性。

4.1 控制器设计

由系统的稳态特性曲线控制可知，系统呈线性特性。实际上，在系统运行过程中受其他干扰影响，系统具有慢时变特性。在某一时间段设计的控制器在系统发生时变后其特性并不能达到最佳效果。为了使控制器发挥最佳效果，需要根据系统模型参数实时更新控制器参数，即控制参数是依赖于控制状态的。加上阵风具有随机性，而这种随机性是由多个不同振幅和频率的正弦波组成。为模拟风环境，需要不同的正弦波风速，这种正弦风具有重复特性。因此，采用基于迭代学习的自校正PID控制可以有效实现正弦风的模拟。

4.2 控制参数与结果

通过前期数值模拟发现，在地面以上1.0m范围内具有较强的风速可控性。图6给出虚拟测点支架示意图，序号(1，2，…，i，…，N)代表N个竖直支架。每个支架上布置n个测点，测点位置根据需要设定。各支架上风速分布均应满足对数廓线，具有唯一的

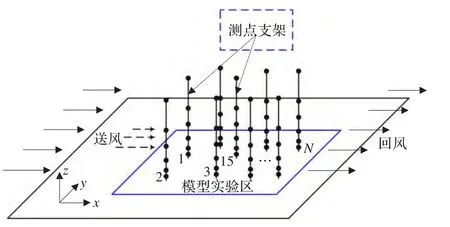
图6 支架位置示意图

其中u*为摩阻风速，z0为地面粗糙度。

实际上，支架位置不同，u*可能不同，但目标是希望获得整个模型实验区整场均一的u*，此时被控参数是u*。实际上u*仅是一个虚拟速度，可根据u*的设定值按竖直方向的风速廓线获得实际流场各点的设定值。

图7给出了图6中虚拟测点支架1、3、15和N位置处基于CFD的风速控制系统仿真结果。这里采用的控制算法为PI控制，比例增益为0.6，积分增益为0.03，u*设定值为0.2m/s。由结果可以看出，不同位置的测点支

风速廓线如下式：架上的速度近似满足对数风速廓线，各处的廓线基本一致，说明其u*值也保持一致，约为0.2m/s。

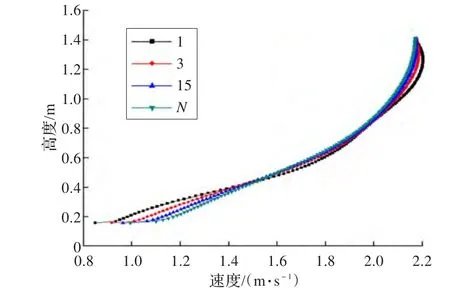
图7 风速廓线数值模拟结果

实际控制时采用基于迭代学习控制的自校正PID控制。为验证控制器性能，对模型实验区中心处支架上的风速进行闭环控制。支架上共布置6个测点，测点距地面高度依次为0.15m，0.2m，0.3m，0.45m，0.67m和1m。设定CFD数值模拟中的控制器增益为当前控制器增益的初始值（比例增益为0.6，积分增益为0.03）。图8给出了不同u*设定期望值下高度为0.67m处的风速控制结果与控制量（图中的风速设定值由给定的u*设定值按照式（8）推得）。

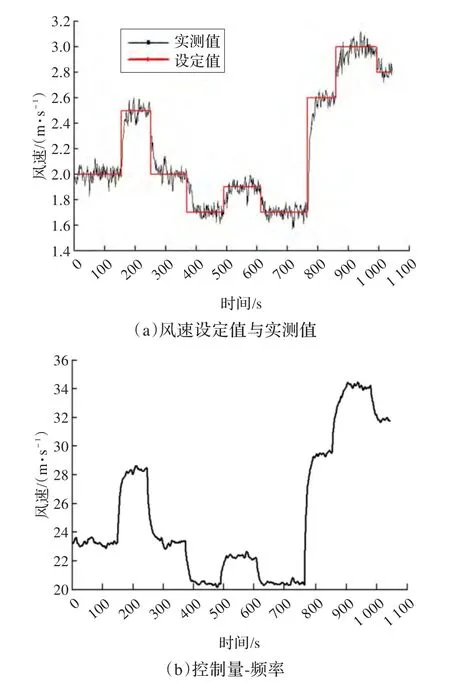
图8 风速控制结果

图9给出了不同时刻风速在高度上的分布廓线。由于整个控制过程中速度变化范围较大，对风速分布廓线进行了无量纲化处理。图中z表示高度，h为高度尺度，u为水平时均风速，U为水平来流速度尺度。由图8可知，系统实际值能够实时跟踪设定值，由于控制系统进行了在线参数估计，并实时更新控制器参数，实现了不同工况下期望风速的无差控制，保证环境模拟中其他动态风速期望的可靠实现。在高度方向的分布特性取决于被动控制值方式的可靠性，由图9可知，在动态控制过程中，高度方向的风速分布基本满足对数廓线分布。

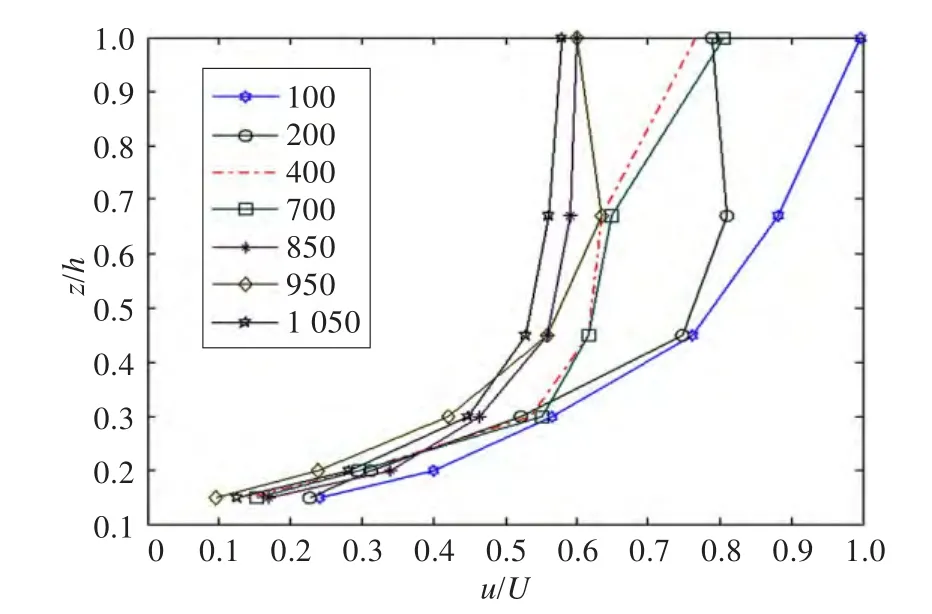
图9 不同时刻时的风速分布廓线

图10给出了设定值为正弦u*风速信号的控制效果和控制量。

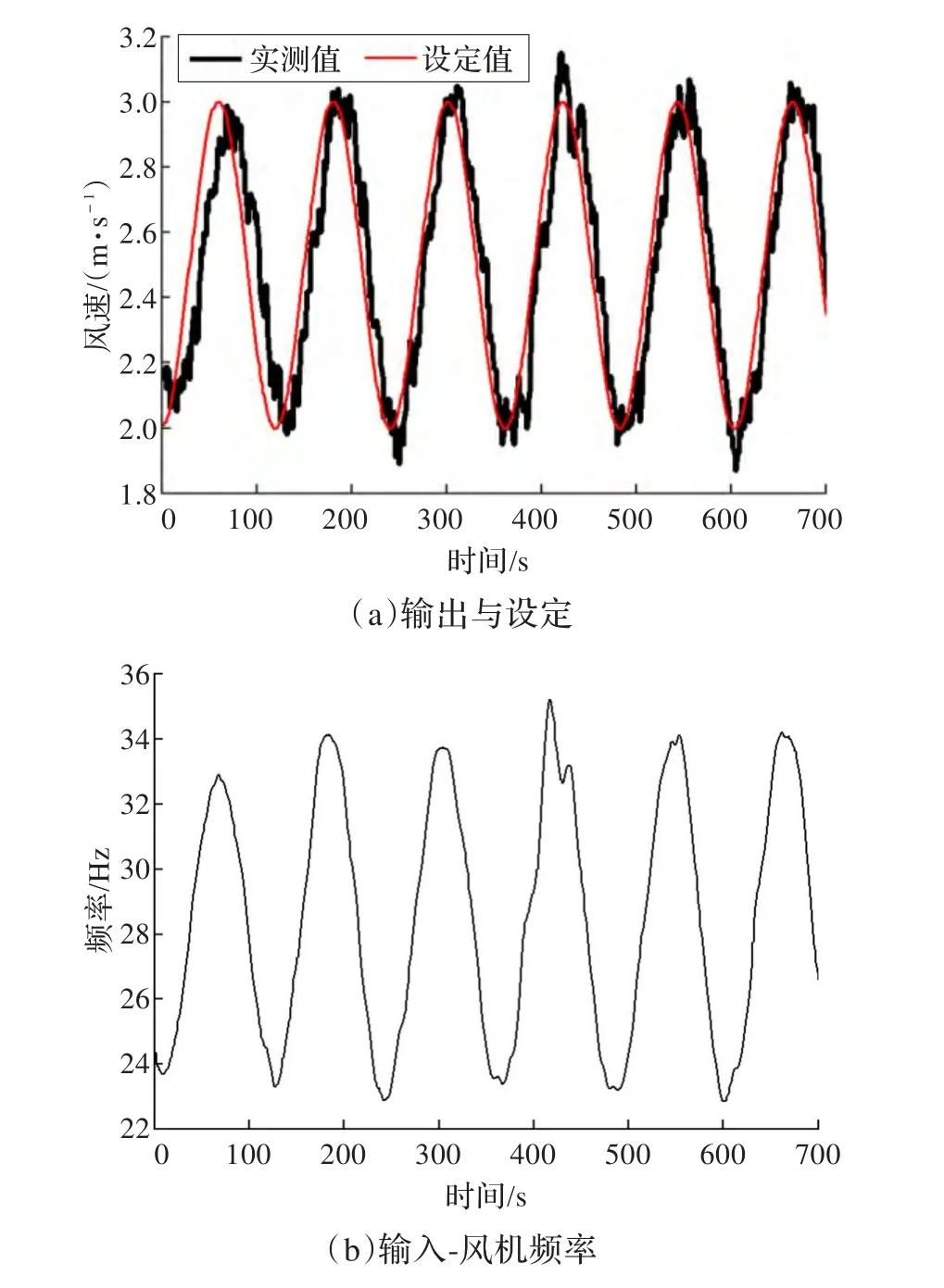
图10 正弦风速控制响应

由图可以看出，在第一个周期控制结果并不理想，实际值与设定值有0.3m/s左右的误差，且实际值较设定值滞后约5 s。经过一个周期后，由第二个正弦周期开始，由于迭代学习控制的作用，实际值已基本跟踪设定值。而且，在440 s时给系统一个干扰，可以看出，系统经过短暂调节，很快使输出跟踪设定。

5 结论

（1）仿真和实验结果均表明，本文提出的控制算法针对风环境模拟的系统控制可行；

（2）实现了对期望风环境参数的有效控制，控制系统具有较强的鲁棒性；

（3）由于迭代学习控制的作用，对于正弦风的模拟，随着时间推进，实际值可跟踪定值，保证了环境模拟的控制精度。

[1]王俊，黄本诚，万才大，等.环境模拟技术[M].北京：国防工业出版社，1996.

[2]M oinn A S，Obukhov A M.Basic law s of turbulentm ixing in the atmosphere near the ground[J].Tr Akad Nauk SSSR Geofiz inst，1954，24（151）：163-187.

[3]李云峰，吴胜兴.现代混凝土结构环境模拟实验室技术[J].中国工程科学，2005，7（2）：81-85.

[4]徐俊，蒲亮，厉彦忠，等.人工环境室内湿度场的数值模拟和优化[J].西安交通大学学报：自然科学版，2007，41（1）：77-81.

[5]川戴玉英.汽车空调环境模拟实验室设计及特点[J].空调与制冷，2002，2（4）：36-39.

[6]肖飚，金苏敏，史敏.人工环境试验室内空气流场的研究[J].制冷与空调，2007，7（5）：89-92.

[7]Mervis J.Bye，bye Biosphere 2[J].Science，2003，302（19）：2053.

[8]孟庆龙.近地层微气候环境模拟与基于CFD的控制方法研究[D].西安：西安交通大学，2010.

[9]A rimoto S，Kaw amura S，M iyazaki F.Bettering operation of robotics by learning[J].J Robotic System，1984，1（2）：123-140.

[10]刘山.迭代学习控制系统设计及应用[D].杭州：浙江大学，2002.

[11]Ruan X iao’e，Wang Jianguo，Wan Baiw u.Filter-based iterative learning control for linear large-scale industrial processes[J].Journal of Control Theory and Applications，2004（2）：149-154.

[12]Xu J X，Xu J.On iterative learning from different tracking tasks in the presence of time-varying uncertainties[J].IEEE Trans on Syst，Man，and Cybernetics，2004，34（1）：589-597.

[13]Ruan X iao’e，Zenn Bien Z，Park K H.Decentralized iterative learning control to large-scale industrial processes for nonrepetitive trajectory tracking[J].IEEE Transactions on System s，Man and Cybernetics：Part A Systems and Humans，2008，38（1）：238-252.

[14]万百五，黄正良.大工业过程计算机在线稳态优化控制[M].北京：科学出版社，1998-06.

[15]Ruan Xiao’e，Hou Zhuosheng，Wan Baiwu.The iterative learning control for the course of steady-state hierarchical optim ization of linear large-scale industrial processes[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation，Shanghai，P R China，2002.