基于小波Contourlet系数相关性的红外图像增强算法

万智萍

（中山大学新华学院，广东 广州510520）

红外图像现如今已被广泛地应用于军事与民用等领域，但由于外界环境的影响或探测器自身设备的影响，使得采集回来的红外图像的噪声量要比普通的图像多，严重影响到信息获取与传输；因此，对红外图像的处理研究具有很重要的意义。为了得到更为清晰的红外图像，人们提出了很多红外图像优化算法，其中图像增强算法能够在保留图像自身信息的同时提高图像的视觉质量或者突显出某些特征信息[1-2]，使得采集回来红外图像比较清晰，便于人们信息的获取，并且该算法也比较适合于红外图像方面的运用。传统的图像增强算法根据性质的不同可以分为空域滤波与频域滤波，而这些方法都具有一个共同的问题，即在图像增强的同时会放大噪声。因此，为了能使算法保留图像增强的特性，同时有效的抑制噪声；选用小波Contourlet变换，该变换是在Contourlet变换[3]与小波变换[4]为基础上的一种改进的新兴算法，通过将这两种算法进行结合，实现这两种变换的优势互补，最终能够更好地捕捉图像的边缘信息。因此,本文根据小波Contourlet变换具有的多分辨率的、局域的、多方向性，提出一种基于小波Contourlet系数相关性的红外图像增强算法，该算法利用各层间小波Contourlert换系数的相关性[5-6]，来对小波Contourlet变换系数进行分类，第一类是对相关性小的小波Contourlet系数进行去噪处理；而第二类则是对相关性大的小波Contourlet系数进行边缘优化处理；并根据各层间系数的相关性与当前系数的所在层数，提出了一种适用于本文算法的阈值选择方法，来获得更好的去噪与边缘优化效果，实现算法的最优化。

1 小波Contourlet变换

小波Contourlet变换由Ramin Eslami和Hayder Radha于2004年提出。根据小波变换与Contourlet变换的不同特性；即小波变换的画笔只能用不同大小的正方形的刷子画轮廓，随着分辨率的加细,使得小波变换的画笔具有局限性,需要许多更细的点来描述轮廓；而Contourlet变换的画笔，是通过沿着轮廓不同方向产生不同大小的长方形,使得该变换可以更有效地抓住轮廓光滑性的特征。其中小波变换能够很好地捕获图像的奇异点却无法很好的表示它，而Contourlet变换能很好的将其表达却不能很好的对其进行捕抓[7]；因此，本文采用小波Contourlet变换对图像进行分解，来实现以上两种变换的优势互补，使其更适用于采集回来的红外图像。图1为小波变换与Contourlet变换曲线。

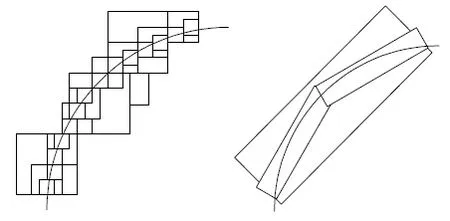
图1 小波变换与Contourlet变换曲线

小波Contourlet变换可以分为两个滤波阶段。第一阶段是先进行子带分解，用小波分解实现；第二阶段是进行方向变换。第1阶段的小波变换每一级是将上一级的低频分量再分解为低频和LH、HL、HH共3个高频部分。在第2阶段，方向滤波器将各个子带进行2N方向的分解，将分布在同方向上的奇异点合成为一个系数。最终得到图2为小波Contourlet变换示意图。

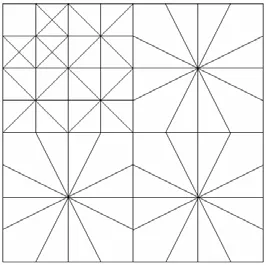
图2 小波Contourlet变换示意图

高频部分主要存储的是图像的细节对其中部分小波系数进行处理不会影响图像重构质量；而最低频子带存储的是图像的主要信号，通常对其进行修改容易破坏原始图像的总体架构；因此，本文只对分解后的高频子带进行处理。

通过方向滤波器后，可以得到如下离散小波Contourlet变换公式：

其中，Wφ(j0,m,n)，(j,m,n)，(j,m,n)，(j,m,n)分别为小波Contourlet变换的低频分量、水平高频分量、垂直高频分量以及对角线高频分量，φ为小波函数，MN为图像大小；其函数的重构公式为：

图3为各频率方向子带的频域分布图。

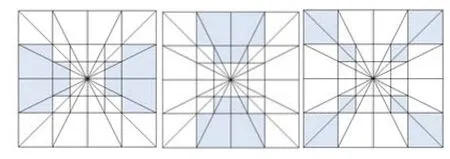
图3 各频率方向子带的频域分布图

2 本文算法

2.1 小波Contourlet系数的相关性

通过对小波Contourlet系数的研究发现：尽管小波变换和Contourlet变换都具有去相关性质,来保证红外图像经变换后的能量集中在有限的变换域系数上；但红外图像经过小波Contourlet分解后，在其高频子带中相邻尺度间的小波Contourlet系数依然存在着很强的相关性，而噪声的小波系数则弱相关或不相关[8]；根据这一特性，根据图像中各尺度间的相关性大小来估计小波系数。

先采用小波Contourlet分解，对其进行3个方向的相关性计算法，即水平方向、垂直方向以及对角线方向的相邻尺度间同一空间位置上的小波Contourlet系数进行乘积运算，其中图像的相关性：

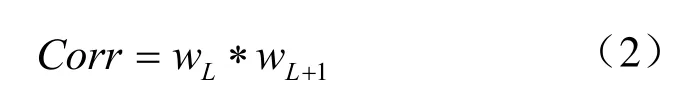
计算可得第L层相关性的总功率和小波系数的总功率，其相关性与小波系数的总功率如下：

而为了得到更为精确的图像中各子带间的图像相关性，对该相关性公式进行完善，本文对其图像的相关函数表达式进行改进，通过引入图像高频子带中各方向子带间的系数比，可得到图像各方向子带中各层小波系数的差异比，即令其函数表达式为：

最终得到相关值：

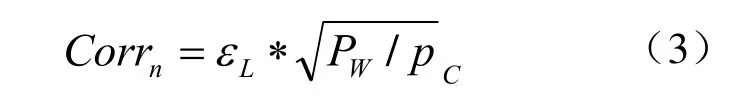
针对水平、垂直与对角线3个方向分别进行小波Contourlet相关性计算，并计算法其最大值与最小值，为图像的小波Contourlet系数的分类运算提供依据；为了方便运算，本文对其相关值进行定义，令ρ=CorrL。相关值的最小绝对值：

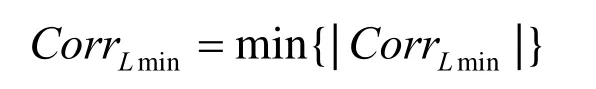
相关值的最大绝对值：

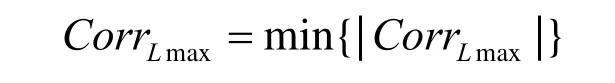
2.2 小波Contourlet系数的分类

通过结合上述的小波Contourlet分解后，分别对不同方向的高频子带进行相关性求解，并根据其相关性的大小，根据以下小波Contourlet的系数特性，文章对其进行分类。

特性 1：在红外图像中，信号和噪声在小波域内具有不同的相关性，信号在尺度间相应位置上的小波系数具有很强的相关性，而噪声的小波系数则具有弱相关性或者不相关；

特性 2：小波变换和Contourlet变换都具有去相关的性质，但是系数间仍然存在着一定的相关性，例如层间对应位置上的系数表现出较强的相关性。

即对图像的高频子带各层间进行小波Contourlet相关性运算，对3个方向的高频子带分别进行小波Contourlet的相关值运算，最终得到如下小波Contourlet系数分类。

相关性小：当0＜ρ≤CorrLmin时，则表明区域小波Contourlet系数的相关性很弱，即主要由图像的噪声信号和少量的图像信号组成，为了得到更为优质的去噪图像，本文对该区域进行小波Contourlet去噪处理以及弱边缘的提取。

相关性大：当CorrLmin＜ρ时，则表明区域主要存放的是图像的有效信号，为了更好地对图像进行处理，本文根据其相关值的大小再次进行分类，并进行边缘优化处理。

2.3 分类处理

2.3.1 降噪处理

红外图像中有效信号在尺度间的相应位置上的小波系数具有很强的相关性，而噪声信号在小波域内由于是随机且均匀分布的，根据这一特性，可以知道噪声信号具有很弱的相关性或不具备相关性。本文根据该性质对噪声信号进行处理，采用阈值去噪算法，通过对软阈值去噪算法进行改进，来得到优化的去噪阈值算法。

传统的阈值去噪算法有硬阈值去噪算法与软阈值去噪算法，如下所示。硬阈值去噪函数：

软阈值去噪函数：

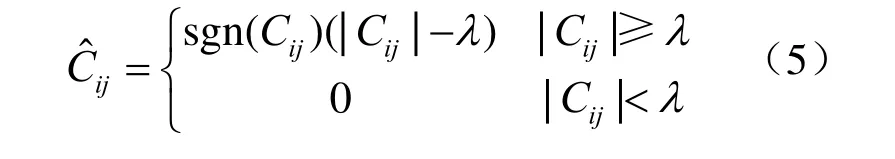
其中，Cij为小波Contourlet系数，λ为阈值；

图4为硬阈值信号曲线图、图5为软阈值信号曲线图。

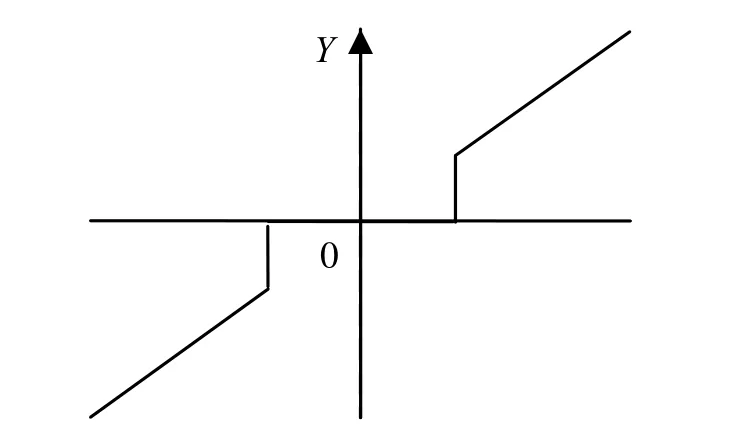
图4 硬阈值去噪曲线图

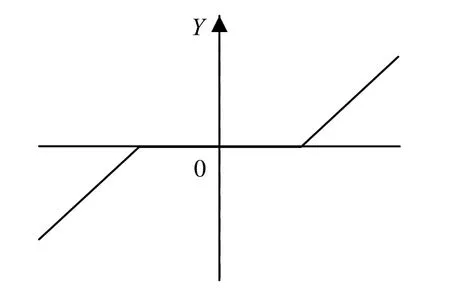
图5 软阈值去噪曲线图

通过对上述两种去噪算法进行研究，软阈值去噪算法相对于硬阈值去噪算法，其计算量相对较大，但其去噪效果较好；而本文采用软阈值去噪算法对相关值0＜ρ≤Corrnmin范围内的小波Contourlet系数进行去噪；在算法的去噪过程中，算法只对相关值较低的小波Contourlet系数进行去噪处理，使得计算法量相对较小，因此，本文采用软阈值去噪算法进行图像的去噪处理，通过结合其系数的相关性对软阈值去噪算法进行改进，如下：

对相关值介于0＜ρ≤Corrnmin的范围内进行降噪处理，但该领域中往往有一部分有效信号也表现出较弱的相关性，因此，如果一味的将其删除，将会使图像的有效信号缺失，进而影响到最终整体的效果，为此，设需要进行降噪处理的图像信号为I=f+n。

其中，f为图像信号，n为噪声信号,本文通过对软阈值去噪算法进行改进，得到小波Contourlet变换图像的降噪处理函数，其函数的表达式定义如下：

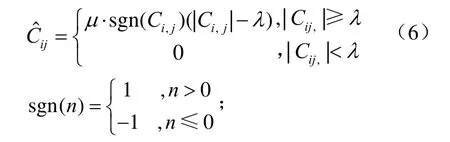
其中，μ为权值常数，λ为阈值，其中阈值λ选取的好坏直接影响图像的降噪处理，而传统的阈值λ=由于没有考虑不同子带和不同分解级数上的差别，容易造成“过扼杀”现象；因此，本文通过结合各子带与分解级数的不同的性质，采用下面提出的阈值选取方式，对其小波Contourlet系数进行判断；

根据反复实验对权值μ进行定义，令μ值为0.6，将其代入Contourlet 变换图像降噪公式中，则有以下公式：

2.3.2 边缘信号强化处理

在相关性较强的区域，为了更好的对其小波Contourlet系数进行边缘优化处理，文章将该区域分为两个不同的区域并对其进行处理；通过小波分解后的高频子带中，高频子带中主要存储的是图像的细节信号，其中图像中的边缘信号主要存放于高频子带。为了验证其边缘信号与系数相关性大小的关系，下面对其进行检验。

在MATLAT 7.10.0的仿真软件中进行边缘检测，文章采用边缘检测算法对图像进行边缘检测，通过定义尺度2j时函数f(x,y)小波变换小波系数模与幅角表达函数对图像的边缘信号进行检测[9]。

模：

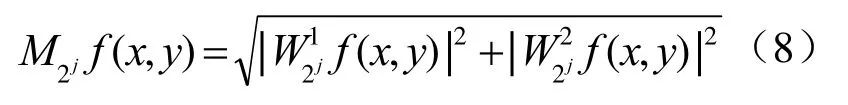
幅角

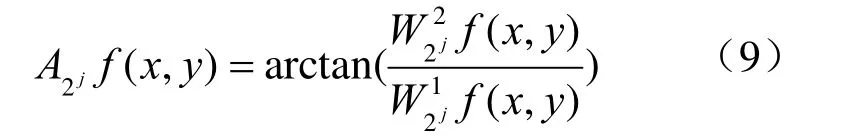
通过反复实验，得图6为图像相关性与边缘信号的关系图。

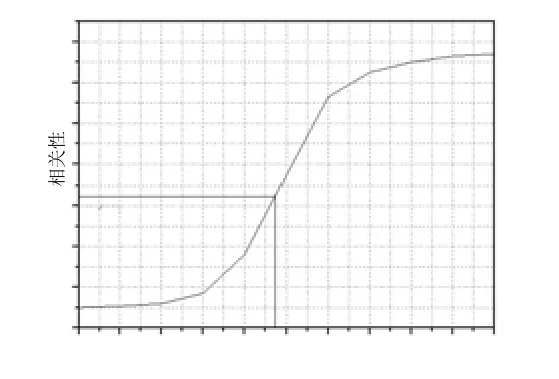
图6 图像相关性与边缘信号的关系图

由图6可以看到，随着边缘强度的不断加强，图像中的相关性也随着不断的增强；通过对相关性值的分析可以区分边缘信号的强弱；因此，本文在相关性与边缘强度信号曲线上增加了当0.45Corrnmax的临界点，来为边缘信号的划分提供依据，定义如下：

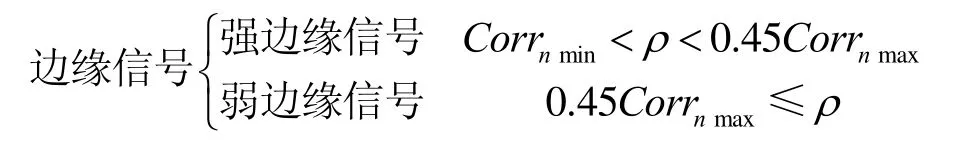
而边缘信号较强的信号可以对其进行适当的弱化，对于边缘信号较弱的边缘信号则是要对其进行强化；因此，本文通过引入边缘增强因子β与弱化因子α，来对图像的边缘信号进行处理，其收缩因子为其中Sx,y为当前的变换系数，N2为原图像的大小，σ为源图像的噪声标准偏差，ρ为小波Contourlet系数的相关值；而弱化因子α的取值范围为(0,1)之间。为了实现对图像信号的边缘信号进行优化处理，本文对其小波Contourlet系数Ci,j进行非线性处理，其中，Cˆi,j为处理后的小波Contourlet系数。

通过对其分类处理，并结合引入增强因子与弱化因子，使图像中较细的细节上细节得以突出，而在图像中较粗的细节上得以弱化，而图像中边缘信号强的进行弱化；最终整理可得边缘处理公式为：

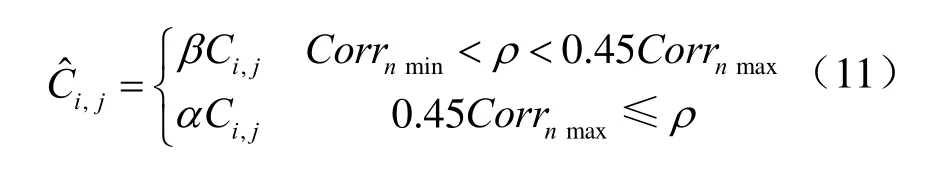
2.4 阈值的选取

通过对比现有的去噪算法[10]，发现这些算法都是通过预先设定阈值，然后对小波系数进行比较判断，但这样会不可避免的出现部分小波系数的误判；传统的小波去噪算法中，由Donoho等人提出的通用阈值公式为：

其中，σ为噪声的标准方差，N2为原图像的大小，这种阈值的设定公式使得在去噪过程中会出现“过扼杀”现象，容易使图像中的有效信号丢失；因此，为了更好的使阈值适用于红外图像，本文更加上述所求得的小波Contourlet系数的相关值并且结合当前的小波分解层数，来提高小波系数阈值判断的准确性,使其更加适应于本文算法的去噪处理，新阈值定义如下：

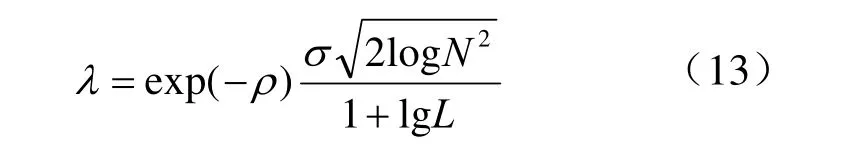
其中，L为当前小波Contourlet的分解系数的层数，ρ为小波Contourlet系数的相关值，通过在其小波阈值原有的基础上，结合小波Contourlet系数的相关性值与所对应的分解层，来提高阈值的适应性，使其更为准确的对相关值介于0＜ρ≤CorrLmin进行有效的图像信号处理。

3 算法设计

算法的具体步骤如下：

Step 1小波分解，对图像进行三层离散小波Contourlet变换分解；

Step 2对分解后的小波Contourlet系数进行水平方向、垂直方向以及对角线方向独立进行小波Contourlet系数运算；

Step 3根据小波Contourlet系数的相关性计算公式，计算出上述3个方向的小波Contourlet系数相关性大小，并根据其相关性的大小来对小波Contourlet系数进行分类；相关值为0＜ρ≤CorrLmin时，对小波Contourlet系数进行改进的软阈值去噪处理，转至Step 4；相关值为CorrLmin＜ρ时，对小波Contourlet系数进行边缘优化处理，转至Step 5；

Step 4采用图像的阈值去噪处理，采用本文所设定的阈值公式(13)，对图像中的噪声信号进行筛选，通过改进软阈值去噪算法，即公式(7)进行去噪处理，最后获得新的去噪小波Contourlet系数，并将其送到Step 6；

Step 5采用图像的边缘优化处理，根据图像中小波Contourlet系数对图像的边缘信号的强弱进行分类；通过引入边缘的强化因子与弱化因子，来对边缘信号进行分类处理；则公式(11)对其边缘优化处理，最后获得新的边缘信号，并将其送到Step 6；

Step 6图像重构，将所获得的图像系数通过小波Contourlet的逆变换重建图像。

4 仿真实验

为了验证本算法的图像增强以及图像的去噪效果，本通过对同一内容与大小的红外图像进行仿真实验，并采用以下几种现有的传统算法进行对比：基于小波变换的图像增强算法、基于Contourlet变换的图像增强算法以及基于小波Contourlet变换的图像增强算法。

采用的红外仿真图像为两幅复杂度不相同的图像；其中猫爪星云红外图像比较简单，而北美星云红外图像相对复杂；并分别加入一定量的噪声量，分别对其进行以上几种算法的仿真实验，得图7为猫爪星云红外图像仿真效果图、图8为北美星云红外图像仿真效果图。

图7 猫爪星云红外图像仿真效果图

图8 北美星云红外图像仿真效果图

通过对以上两种代表复杂程度的图像进行处理，算法对内容简单的猫爪星云红外图像进仿真得图7，可以看出小波Contourlet增强算法的仿真效果优于小波变换的增强算法与Contourlet变换的增强算法以及传统的小波Contourlet增强算法处理后的图像，其中通过观察，可以看到本文算法的清晰度高于其他算法；而当对内容复杂的北美星云红外图像进行仿真得图8，可以看出本文算法优于其他种算法，可以看到本文算法能够在增强图像的边缘信号的同时很好的去除图中的噪声信号；通过结合两个实验可以看到，传统的小波Contourlet增强算法虽然能够得到较好的仿真图像，但其中一些有效的弱小信号被当成了噪声信号被去除了，而本文算法通过引入弱化因子与强化因子的边缘优化算法，使得本文算法依然能够有效的保护图像中的弱小信号；其实验结果与预期的效果相符，有效的证明了算法的可行性；

为了更好的对各算法的仿真效果进行比较，本文通过在MATLAB 7.10.0仿真软件中进行各算法的仿真，在不同的噪声量的环境下，采用的客观评价标准峰值信噪比PSNR对仿真的质量进行评估，经检测，得图9为猫爪星云红外图像PSNR曲线图、图10为北美星云红外图像PSNR曲线图。

本文采用的PSNR函数表达式为：

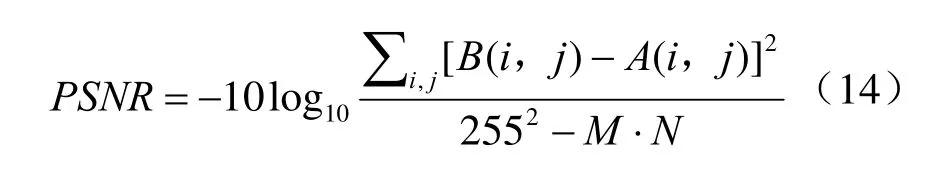
其中，A(i，j)为未加噪的原始图像，B(i，j)为含噪的图像；MN为图像的大小。

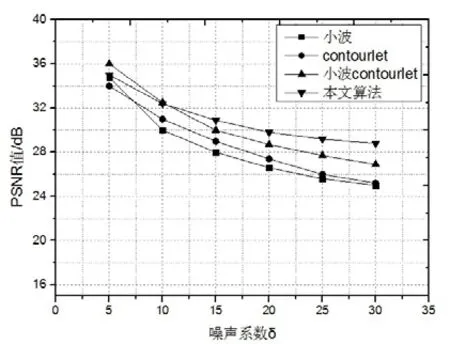
图9 猫爪星云红外图像PSNR曲线图

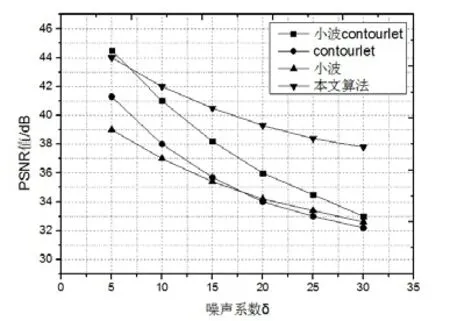
图10 北美星云红外图像PSNR曲线图

通过分析图9各算法的仿真曲线可以看出，算法对于图像信号内容简单的处理效果与其他算法相差无几，随着噪声系数δ的增强本文算法的优势逐渐体现出来，但相对传统小波Contourlet增强算法所求得的PSNR值最高高出2.4dB；而算法对于图像信号内容复制的处理效果优于其他算法，且算法受噪声系数的影响较小，由图10可以看出，其中与传统的小波Contourlet增强算法的PSNR值最高相差4.9dB。

边缘保持指数EPI反映的是原始图像与去噪图边缘对比度之比，去噪后的图像边缘细节保持得越好，其EPI值就越大且最大值为1；通过对各算法处理后的效果图进行EPI值的测量，评价图像的边缘保护效果；经测试，得表1为各算法边缘保护指数数据表，如下所示。

其边缘保持指数函数表达式为：

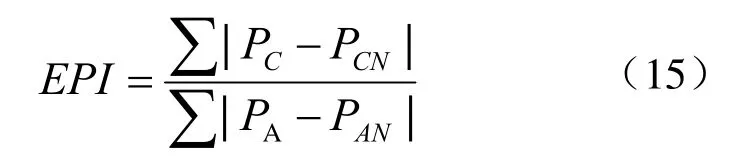
其中，PC为去噪处理后的像素点的灰度值，PCN为PC相邻像素点的灰度值，PA为原始图像的像素点灰度值，PAN为PA相邻像素点的灰度值。

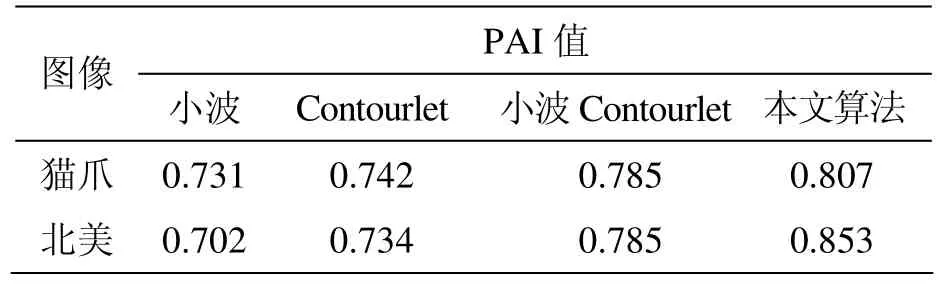
表1 各算法边缘保护指数数据表

由表1可以看出，当在噪声量为20的时候，通过各算法对猫爪星云红外图像进行仿真后，通过对所测得的PAI值进行比较，本文算法优于其他算法，其中本文算法高于小波Contourlet算法，相差0.022；而对复杂度较高的北美星云红外图像进行处理后的仿真数据，本文算法明显优于其他算法，其中比小波Contourlet增强算法高出0.68；有效的证明了算法的显著边缘保护效果。

5 结束语

提出一种基于小波Contourlet变换系数相关性的红外图像增强算法，根据结合高频子带各层间的系数相关性来对子带系数进行合理地分类，其中对弱相关的系数进行去噪以及弱边缘增强处理；而对于相关性较强的系数，则是采用边缘优化处理；最后通过优化阈值的选择方式，来提高算法的去噪以及边缘优化效果。实验结果表明，实验结果与预期目标相符，该算法能够获得比其他算法更好的去噪以及保护边缘信号，但如何提高运算速度是一个值得进一步研究的问题。

[1]Kim S,Kang W,Lee E,Paik J.Wavelet-domain color image enhancement using filtered directional bases and frequency-adaptive shrinkage [J].IEEE Transactions on Consumer Electronics,2010,56(2): 1063-1070.

[2]Kober V.Robust and efficient algorithm of image enhancement [J].IEEE Transactions on Consumer Electronics,2005,52(2): 655-659.

[3]Zhang Xin,Jing Xili.Image Denoising in Contourlet domain based on a normal inverse Gaussian prior [J].Digital Signal Processing,2010,20(5): 1439-1446.

[4]Balster E J,Zheng Y F,Ewing R L.Feature-based wavelet shrinkage algorithm for image Denoising [J].IEEE Transactions on Image Processing,2005,14(12):2024-2039.

[5]He Yanmin,Gan Tao,Chen Wufan,Wang Houjun.Multi-stage image Denoising based on correlation coefficient matching and sparse dictionary pruning [J].Signal Processing,2012,91(1): 139-149.

[6]Eslami R,Radha H.Translation-invariant Contourlet transform and its application to image Denoising [J].IEEE Transactions on Image Processing,2006,15(11):3362-3374.

[7]Cunha A L,Zhou J P,Do M N.The Nonsubsampled Contourlet transform: theory design and applications [J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.

[8]Rajpoot N,Butt I.A Multiresolution framework for local similarity based image Denoising [J].Pattern Recognition,2012,45(8): 2938-2951.

[9]Kao Wenchung,Chen Yingju.Mltistage bilateral noise filtering and edge detection for color image enhancement [J].IEEE Transactions on Consumer Electronics,2005,51(4): 1346-1351.

[10]Binh N T,Khare A.Multilevel threshold based image Denoising in Curvelet domain [J].Journal of Computer Science and Technology,2010,25(3): 632-640.