滚珠丝杠副热变形计算分析及可视化

李凌丰，管灵波，张振然，陈 豪

（浙江大学机械工程学系工程及计算机图形学研究所，浙江 杭州 310027）

目前，随着塑料原料价格和性能的提高，塑料制品逐渐向小型化、轻量化方向发展，主要表现为：其一是制品尺寸精度较高；其二是薄壁制品。然而传统的液压注塑机无法很好满足要求，首先是液压系统的能耗大，易转变成热能引起温升，影响合模精度；其次是容易漏油，而部分产品诸如医疗器械等对清洁环境要求较高。在此背景下，全电动式注塑机凭借节约能源、清洁低噪、控制性能优良等几大特性[1-3]成为注塑行业的发展方向[4]。

然而，全电动式注塑机的软肋在于锁模机构[5]，而滚珠丝杠副和拉杆是锁模机构的关键传动元件，其中滚珠丝杠副主要由丝杆，螺母件及滚珠等组成，借助滚珠返回通道构成滚珠的闭合回路，实现往复螺旋传动。这两个传动元件的不足表现为：一方面因为采用肘杆式锁模机构，此结构易磨损；另一方面，液压驱动改成由伺服电机带动滚珠丝杠来驱动，锁模压力大部分由丝杠承受，特别是在高速的工况下，将极大地降低丝杠的精度和缩短使用寿命，限制了注塑机在大吨位注塑领域的应用。对前者国内有颇多研究，主要进行结构改进，如胡静和张有忱[6]讨论了差动式齿轮锁模机构特点，又如焦志伟等[7]将三板肘杆式改成二板直压式。因为温升对合模精度影响显著，这与注塑机高精度要求相悖，本文探讨温升对滚珠丝杠精度的影响。

国内对滚珠丝杠的研究多集中于车床，虽然与注塑机的工作条件有所不同，但是仍具有借鉴性，如易学平[8]分析丝杠机构热变形的原因，并给出了实际工况的温度场经验公式；夏勇军[9]通过有限元方法研究了多变化热源作用下滚珠丝杠的热动态特性的分析，获得进给系统热误差的辨识模型；钟名东[10]、王淑坤[11]分析滚珠丝杠副的温度场，通过热——结构耦合仿真，求解热变形，研究其热态特性。本文基于传热学理论，分析滚珠丝杠的热边界条件，利用有限元软件对滚珠丝杠副进行热仿真，获取滚珠丝杠副的稳态温度场和热变形数值结果，通过云图、矢量图等数据场可视化方法，直观地展示滚珠丝杠运行时的热传递和热变形规律，分析后提出减少热变形影响的预防措施。

1 热分析基本理论

1.1 传热的理论基础

滚珠丝杠副的热变形与热量的传递及温度分布密切相关，根据传热的物理本质，热量传递有3种基本方式：导热、对流和辐射。

（1）导热

导热是指热量从物体（包括静止的液体）高温部分传递给低温部分，或者从高温物体传递给相接触的低温物体。导热与温度场息息相关，温度场描述了空间内任意点在某一瞬时的温度值分布，所以温度场是空间和时间的函数，温度T用位置坐标x，y，z和时间τ可以表示为[12]：

各点温度随时间变化的温度场被称为瞬态温度场，如式(1)；若温度的时间变化率很小，则温度场被称为稳态温度场，如式(2)，本文将探讨滚珠丝杠副的稳态温度场。

温度场中相同温度的点连接成的曲面即等温面，这常用于描述温度场。因为物体内任一点某一瞬时的温度值是唯一的，所以等温面不相交且连续。温度场的分析可借助温度梯度(gradT)，所谓温度梯度是指等温面法线方向温度增量与法向距离之比的极限，见式(3)，可以表征温度场内任意一点在垂直其所在等温面方向上的温度变化的强烈程度。温度梯度的方向与等温面的法线方向相一致，但与热流量的方向相反。

在温度场中，非等温面方向的温度是变化的，因此会发生热量传递，可以用热流密度来表征，即单位时间内通过等温面单位面积的热量。热流密度的方向是沿着等温线法线而指向降温的方向。温度场的温度与热流密度通过Fourier基本导热定律[12-14]联系起来：

式中，q为热流密度(W/m3)；λ为热导率(W/m· K)。

（2）对流换热

对流换热是指流体流经固体表面时，两者之间发生的热交换，这是流体的对流和导热联合作用的结果。对流传热可分为强迫对流与自然对流：自然对流是由于流体冷热不均所引起的流动；强迫对流则是由于压差引起的。

对流换热的强度通过对流换热系数(h)表征，指单位时间内温差为1的单位表面的对流传热量[12,14-15]。

式中，h为对流换热系数(W/m2·K)；D为几何尺寸(m)；Nu为努塞尔数（无量纲），壁面上流体的温度梯度。

对流换热系数受较多因素影响，如流体物性，流动状态等等，所以该系数较难确定，常用的方法是针对特定的物理现象，将众多的影响因素组成几个无量纲参数，如雷诺数Re，这是表征惯性力与黏性力的一种度量，反映了流体的流动状态，可通过下式确定：

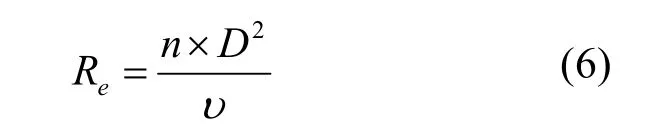
式中，n为丝杠转速(r/min)；υ为运动黏度(m2/s)。

确定无量纲参数后，通过实验确定包含无量纲参数的准则方程，这类方程概括性地归纳了主要物理量的关系，如下是两类特定现象的对流准则方程。

① 流体沿着平壁强迫流动

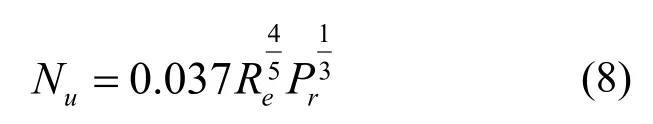
式中，Pr为普朗特数（无量纲），动量扩散厚度与热量扩散厚度之比的一种度量；vf为流体的线速度(m/s)。

② 流体沿着单管强迫流动

局部表面传热系数变化比较复杂，但从平均表面传热系数看，渐变的规律性很明显，可采用如下准则方程[12]：

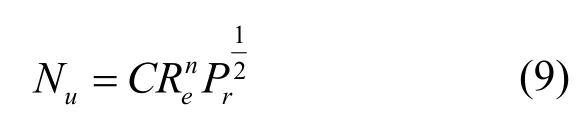
式中，C，n为常量，需要查表获取。

根据式(7)～式(9)，可求得Nu代入式(5)，即可求得对流换热系数。

（3）辐射传热

辐射传热是物体以电磁波方式向外传递能量的过程，被传递的能量就是辐射能。热辐射的能量。热辐射的能量投射到物体表面时，发生吸收，反射和穿透现象，而固体可以认为无法穿透，所以辐射传热主要通过吸收。

通常，辐射传热多在凸体之间通过大气或真空中进行，滚珠丝杠副表面A1与外界热源表面A2(如注塑机其他部件，车间墙壁，地面等)之间辐射传热，辐射传热系数[12,14-15]可根据下式：

如果A2＞＞A1，则

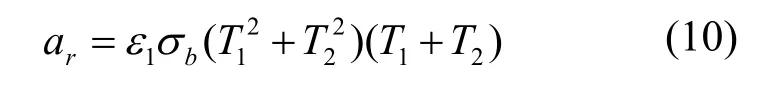
如果A2≈A1，则

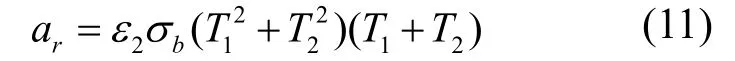
式中，ar为辐射传热系数(W/m2·K)；1ε，2ε由温度T1和T2决定；bσ为斯忒藩-玻耳兹曼常数，其值为5.7×10-8W/(m2·K4)；T1为机床壁面的热力学温度(K)；T2为外界热源，可近似取周围大气的热力学温度(K)。

1.2 导热微分方程

根据热力学第一定律，系统内能的总增量等价于内热源的发热量和进出的热量差的总和，如下：

式中，dE为系统内能总增量；dQg为内热源的发热量；dQ为进出的热量差，取为零。

各项用傅里叶方程式展开后，可得：

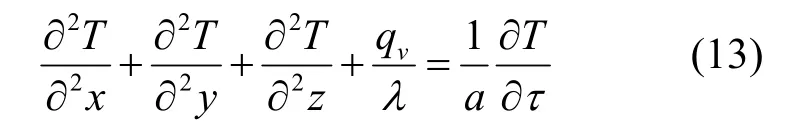
式中，qv为单位体积单位时间内的热源发热强度(W/m3)；a为热扩散率(m2/s)；λ为导热系数(W/(m·K))。

本文中的滚珠丝杠副系统经过预热后，温度升高并达到稳定状态，稳定后的滚珠丝杠副系统可视为“热源”的稳态传热，式(13)可改成泊松方程[12]：

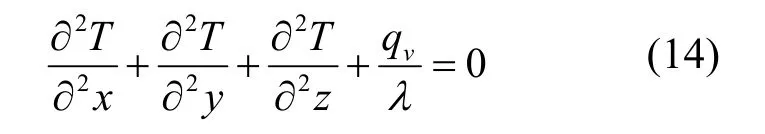
1.3 单值性条件

导热微分方程是由传热的一般规律推导出来的，代表无数种彼此不同的导热现象。如果要研究某种导热现象，就必须将其特点表示成数学式，并与导热微分方程联立求解，表述这些特点的数学式成为单值性条件。单值性条件主要指初始条件和边界条件，对于稳态温度场只需要确定边界条件即可。边界条件是指物体边界表面与周围介质之间的传热情况，有三类[12,14,16]：

（1）第一类边界条件：已知物体边界Γ上温度场。

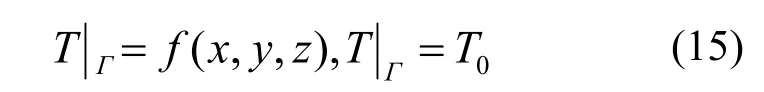
式中，T0为已知温度，f(x,y,z)为已知温度函数。

（2）第二类边界条件：已知物体边界上Γ的热流密度。

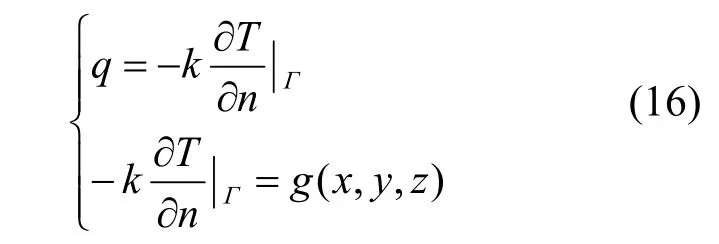
式中，q为热流密度(W/m2)；g(x,y,z)为热流密度函数；k为传热系数(W/(m2·K))。

（3）第三类边界条件：已知与物体相接触的流体介质的温度和换热系数。

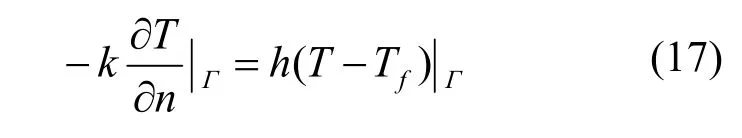
式中，Tf为流体介质的温度(K)；h为换热系数(W/m2·K)，在稳态温度场中，Tf和h可以是常数，也可以是随位置而变化的函数。

1.4 热弹性运动方程式

物体随着温度升高而膨胀，温度降低而收缩，这种由于温度改变而引起的变形称为热变形。以平面微元体应力问题为例，当温度由T0变成T时，温差ΔT=T-T0，热变形只产生线应变[10,13]：

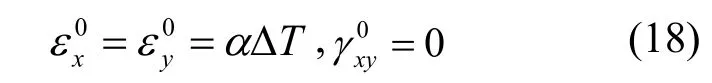
式中，xε，yε分别为x，y方向的正应变；γxy为切应变。

假设物体的膨胀完全不受约束，那么物体内不产生热应力。当物体受约束或者各部分温变不均匀，热变形无法自由进行，热应力就产生了。

热应力和热应变的关系可以根据胡可定律[10-11]得到

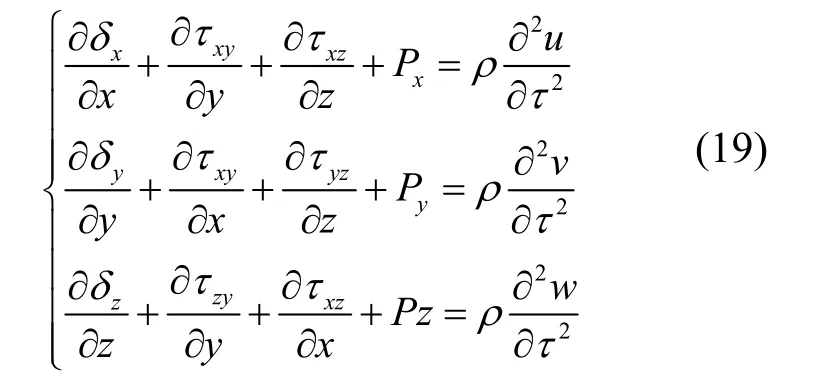
式中，δx,δy,δz分别为x,y,z方向的正应力；τxy,τyz,τxz分别是x,y,z方向的切应力；ρ为密度(kg/m3)；u,v,w为变形时物体某一点在x,y,z方向的位移分量；Px,Py,Pz分别为x,y,z方向的体力。

进一步推导可得用位移分量表示的热弹性运动方程[10,11]：

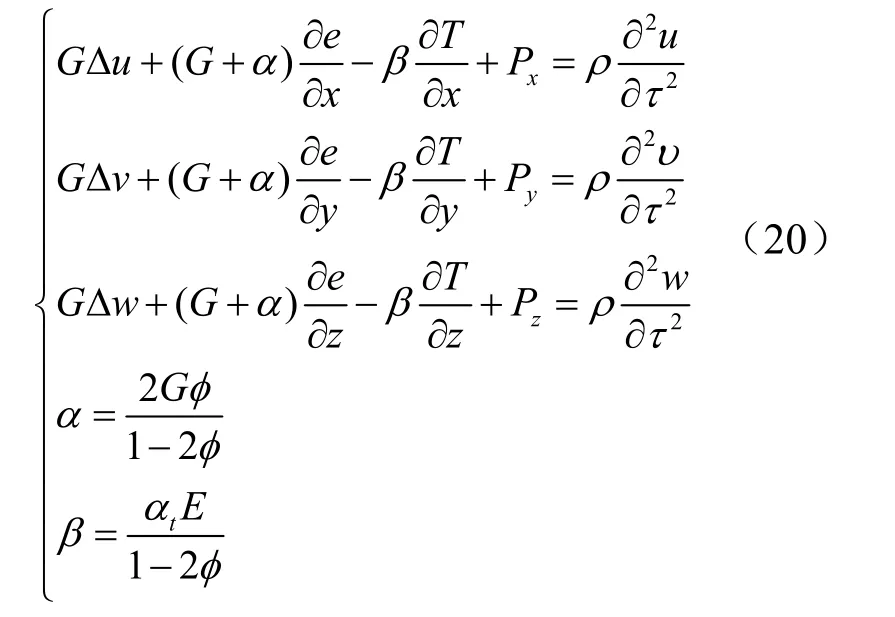
将式(20)用矢量表示[10,13]，并忽略重力，则可得：

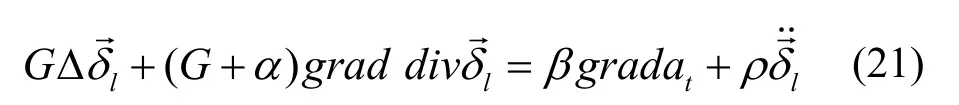
式中，为u,v,w。

2 滚珠丝杠热边界条件计算

滚珠丝杠副的结构如图1，本文中滚珠丝杠采用一端由轴承支撑，呈悬臂状态[17]。有限元热分析的第一步是确定热边界条件。根据滚珠丝杠的工作特点，主要考虑热传导和对流两种传热方式，而忽略辐射传热。

图1 滚珠丝杠副的三维模型

2.1 滚珠丝杠副的参数

本文选用某型号滚珠丝杠副，其相关参数为：轴径d=63mm，导程为Ph=12mm，总轴向载荷Fa=10000N，轴向预紧力Fp=1/3Fa=10000/3 N，转速n=1350r/min，丝杆效率η=94% 。

滚珠丝杠副的材料选择轴承钢GCr15[18]，相关参数为：密度ρ=7850kg/m3，抗拉强度σb=1861MPa，平均线膨胀系数α=1×10-6a/℃，导热率λ=36.72W·m-1·K-1，泊松比μ=0.29。

2.2 热传导系数

滚珠丝杠副的内热源来自于摩擦热，主要来自于丝杠和螺母间的相对移动，丝杠与支承轴承间的旋转运动，因为移动螺母直接关系锁模精确性，影响最终成型的精度，着重关注丝杠和螺母与滚珠之间的摩擦热。

滚珠丝杠副运转过程中，滚珠与滚道面之间产生的摩擦热通过接触界面不断向外传导。滚道面之间充满润滑油，润滑油不仅能减少摩擦阻力，同时实现快速导热。最终，当滚珠丝杠副达到工作状态时，丝杆与螺母滚道面之间的温度场应当是均布的，即丝杠与螺母的滚道面之间温度恒定，所以滚道面可采用第二类边界条件，即在滚道面施加恒定的热流密度。

计算热流密度[10,16-17,19]，首先求得滚珠丝杠副的摩擦热量，可以参考滚动轴承的发热量计算公式：

式中，Q为滚动轴承的发热量(W)；M为总摩擦力矩(N·mm)，包括丝杠的驱动力矩Md和滚珠螺旋的阻力矩Mp。

发热量无法作为热载荷直接加载到有限元模型，需要进一步求出热流密度，即热源单位面积的发热量，计算式如下：

式中，S为螺母内滚道面面积(m2)。

2.3 对流换热系数

在高速运转中，滚珠丝杠副的部分丝杠表面总是暴露在空气中，丝杠的强劲旋转势必加快空气对流，这是强迫对流换热。对流换热系数可根据式(8)可得，其常数C，n查阅相关文献[12,15]，可知：

把式(24)带入式(8)可得

根据式(6)，式(24)，式(25)可求得Nu，代入式(5)即可求得对流换热系数。

3 滚珠丝杠副的热分析

3.1 温度场仿真

滚珠丝杠副的几何模型比较复杂，次要特征有必要简化处理[14]，如去除倒角，次要螺纹孔改成光孔，减少滚珠的数量等等，简化后的模型如图1所示。有限元仿真主要有3个步骤：建立有限元模型，施加载荷及边界条件，查看数值结果。

建立有限元模型，需要合理划分网格，在保证单元质量的前提下，通过收缩控制，局部细化等手段，控制单元数，这样在保证求解的精度和准确性的同时，加快收敛速度[11,20]。

由式(5)，式(22)，式(23)计算可知，丝杠滚道面与周围空气的对流换热系数，滚珠滚道面的热流密度，设定空气温度为20。滚珠丝杠副温度达到稳态，即温度T不随时间τ变化，传热方程依据式(14)可知，热源的发热量通过传导完全释放到环境。

丝杆滚道面的各部分载荷不同，首先进行面分割，分别施加热载荷及边界条件；螺母件内滚道面及滚珠导管内表面施加热流密度载荷。载荷设置完成后，求解温度场及热流密度，计算结果如图2所示。

图2 滚珠丝杠副的温度场

由图2可知，丝杆外滚道面的温度与环境温度接近，因为丝杆的高速旋转，极大提高其表面对流换热，使得热量快速散发，温升相对较小，不到1℃。而螺母件的温升最高，特别是滚珠导管处，达到3.8℃。这是由于滚珠与滚道面产生摩擦热，另外螺母件外表面的对流换热强度相对较小，引起热量的积聚。滚珠与滚道面的温度场需要重点考察。

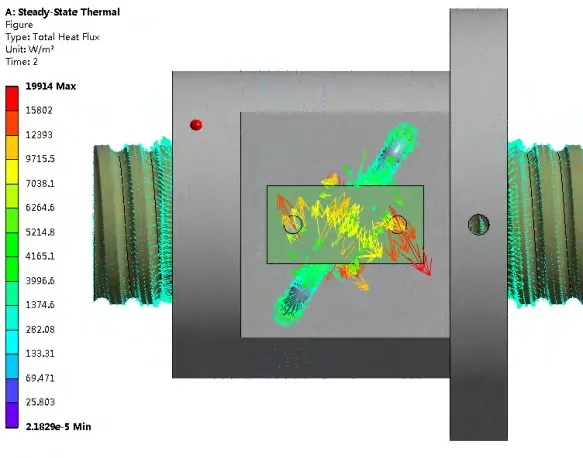
图3 外表面热流密度

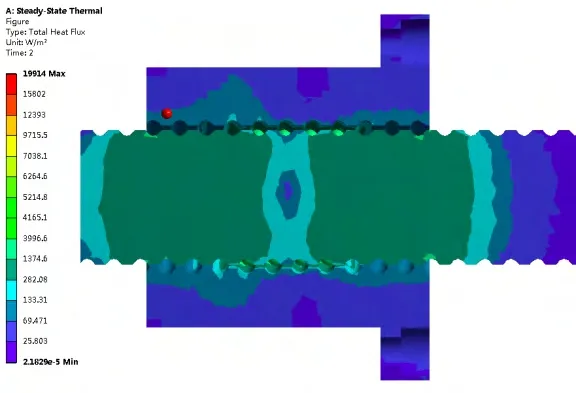
图4 截面热流密度

由图3可知，热流密度最高值为19914W/m2，发生在滚珠导管附近，同时螺母件的热流密度比丝杆要弱。由图4可知，螺母的平均热流密度为80W/m2左右，而与螺母旋合的丝杆部分则达到了700～800W/m2，所以丝杆的散热速度快，温度相对螺母件要低，如图2所示。同时，由图4可知，丝杆的最高热流密度集中在螺母端面处。

3.2 热-结构耦合仿真

热-结构耦合需要导入温度场结果，并对滚珠丝杠副进行约束[20]，如限制丝杆的轴向与径向的移动，限制螺母的径向移动，施加角速度载荷。加载完毕后，计算求解热-结构如下：

图5 滚珠丝杠副的总体热形变

图6 滚珠丝杠副的总体热应力

图7 滚珠丝杠副的总体热应变

由图5可知，丝杆支承端的热变形最小，接近零，由于轴承的径向约束限制其变形，势必导致应力的积聚，如图6可知，支承端的应力及应变最大。丝杆自由端则正好相反，温差使得自由端无约束的膨胀，变形相对较大，达到8.32μm，应变与应力相对较小。螺母件由于温差变化小，其热变形相对较小。

由式(21)可知，热变形量与材料的热物性参数密切相关，所以选择合适材料，能极大改变热变形量。

4 结 论

由于本文的数值仿真是在理想状态下进行，如果考虑外界热源，丝杆的制造误差等因素，热误差数值将放大数倍；此外，滚珠丝杠副正向高速方向发展，速度进一步提升必然引起热变形加剧。因为滚珠丝杠副是传动件，热误差逐级积累，直接影响合模精度，最终影响制品质量。

综上所述，滚珠丝杠副的热误差将降低合模精度，影响最终制品的精度，为控制热变形，可采用预拉伸技术等措施[17,21-22]。预防热变形措施可通过数值计算进行优化，这将涉及到有限元软件的二次开发，这些问题尚待进一步的研究。

[1]黄步明.精密注塑机的最新技术进展及发展趋势[J].中国医疗器械信息, 2012, 18(3): 23-26.

[2]宋春华.高档注塑机的发展动向[J].机床与液压,2012, 40(2): 122-129.

[3]向 鹏, 李绣峰, 杜遥雪.全电动注塑机的特点及应用领域[J].现代塑料加工应用, 2007, 19(1): 5254.

[4]黄步明.全液压式与全电动式注塑机的比较: 2005《中国塑料》论坛暨塑料注塑新技术国际研讨会[Z].上海: 2005.

[5]杨 玥, 王柏村, 纪 国, 袁卫明, 厉永福.全电动精密注塑机及其合模装置的比较与分析[J].轻工机械, 2011, 29(6): 113-116.

[6]胡 静, 张有忱.全电动注塑机差动式合模机构的设计与分析[J].工程塑料应用, 2010, 38(10): 79-82.

[7]焦志伟, 谢鹏程, 严志云, 杨卫民, 王兴天.全液压内循环二板式注塑机性能特点及锁模精度研究[J].塑料, 2009, 38(6): 112-115.

[8]易学平.丝杠结构热变形及近似估算探讨[J].机械工程与自动化, 2011, 133(6): 170-171.

[9]夏军勇.热弹性效应和数控机床进给系统热动态特性的研究[D].华中科技大学, 2008.

[10]钟名东.高速高精数控车床滚珠丝杠进给系统热态特性研究[D].江西: 华东交通大学, 2011.

[11]王淑坤.滚珠丝杠进给系统定位精度分析[D].大连: 大连理工大学, 2006.

[12]杨世铭, 陶文铨.传热学(杨世铭)[M].北京: 高等教育出版社, 2006.

[13]陈兆年, 陈子辰.机床热态特性学基础[M].北京:机械工业出版社, 1988.

[14]俞佐平, 陆 煜.传热学(俞佐平)(第3版)[M].北京: 高等教育出版社, 1995.

[15]张靖周, 常海萍.传热学(张靖周)[M].北京: 科学出版社, 2009.

[16]张朝晖.ANSYS 12.0热分析工程应用实战手册[M].北京: 中国铁道出版社, 2010.

[17]程光仁, 施祖康, 张超鹏.滚珠螺旋传动设计基础[M].北京: 机械工业出版社, 1987.

[18]钟顺思, 王昌生.轴承钢[M].北京: 冶金工业出版社, 2000.

[19]王延忠, 闫 涵, 周元子, 李秀琴, 刘景祎.龙门加工中心主轴系统热态特性分析[J].机床与液压,2008, 36(5): 16-18.

[20]许京荆.ANSYS 13.0 Workbench数值模拟技术[M].北京: 中国水利水电出版社, 2012.

[21]葛继承, 二宫瑞穗.滚珠丝杠的摩擦和温升[J].机床, 1981, (3): 26-29.

[22]江 平.数控机床丝杠预拉伸技术研究[J].机电研究及设计, 2010, (5): 43-45.