边缘识别的二维正交多项式拟合及结构变形检测

袁向荣

（广州大学土木工程学院，广东 广州 510006）

数字图像检测结构变形常用数字图像相关法(Digital Image Correlation，DIC)和边缘检测法(Edge Detection，ED)，DIC法一般是由变形图像和参考图像图案的相似性识别图像变形，ED法是根据边缘两侧灰度的一或二阶导数特征识别边缘位置，DIC是面检测，ED法是线检测，DIC法检测精度可达0.01像素。常用的整像素ED方法有Roberts、Sobel、Prewitt、Laplacian和Canny[1]等方法。结构工程对检测的精度要求很高，常常要求采用亚像素识别，亚像素ED方法有基于矩保持的识别法[2]，正切函数拟合法[3]，基于插值的方法[4]等。袁向荣[5]将DIC法用于边缘识别，研究表明，在梁体没有图案的情况下，二维相关方法精度与一维相关方法相当，但计算量要大很多。ED法检测精度在0.05像素左右。虽然DIC法精度较高，但要求结构表面有明显的图案特征，限制了DIC法的应用。

Fu和Moosa[6]提出用多项式函数拟合边缘灰度，可由函数的连续性求导以识别边缘。袁及其团队对多项式函数拟合法进行了研究，并将边缘识别法应用于梁模型的静动力试验[7-11]。按照泰勒级数公式，多项式对已知函数逼近的精度取决于多项式的阶数，对已知函数的拟合由于级数的各项系数可由函数的导数求得，采用高阶多项式并不难。但对已知数据进行拟合时，须对优化方程进行求解以确定待定系数，但阶数高于7的多项式拟合的优化识别方程，其系数矩阵是病态的，因此次数高于7的多项式不能有效提高边缘识别精度[7,12]。为改善拟合精度，文献[7]提出滑动拟合法，对边缘曲线的拟合精度提高明显 。

Ye等[13]提出一种基于高斯函数边缘模型的识别方法，采用光强函数

式中，h为灰度基值，k为灰度增值，某邻域内设边缘曲线为抛物线Px2+Qx+R，σ为模糊因子。则边缘附近的像素灰度为

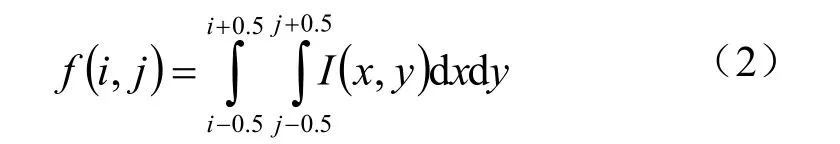
在某领域内取模型灰度与图像灰度Gij的平方差为目标函数，采用优化法识别式(1)中的6个待定系数，以此识别边缘的位置。在实际研究中，阶跃边缘可用高斯模型进行描述，因此已有学者采用这种模型[14-15]。基于高斯模型的边缘识别优于基于矩保持的方法和插值法。此方法边缘识别效果较好，原因应是采用了二维边缘模型式(1)和式(2)进行识别，但式中的参数识别方程为隐式方程，须用非线性优化方法，如采用牛顿-拉尔森法，还须计算梯度和雅可比矩阵，不可避免的要对反常积分进行数值计算，应用上不够简便。现有的多项式拟合法的主要缺点：一是不能采用高阶多项式，限制了拟合精度；二是一维拟合仅考虑跨边缘的灰度变化，未考虑沿边缘的变化，限制了边缘的识别精度。下面介绍二维正交多项式拟合边缘曲面的方法，拟合和识别优化过程无须求逆和解方程，因此不存在病态方程求解问题，可以采用高阶多项式进行拟合，且简便易行。

1 二维正交多项式边缘拟合法

对于图像中某边缘领域的灰度曲面f(x,y)在矩形网格点(xs,yt),s=0,1,…,n;t=0,1,…,m的型值已给。选定一组乘积型基函数并假定n≥N，m≥M。可用最小二乘法寻求二元曲面

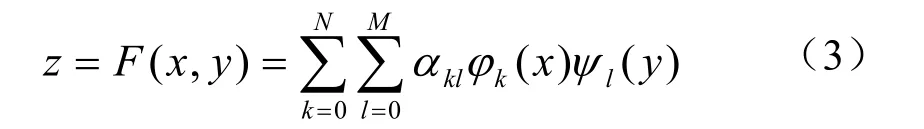
由目标函数

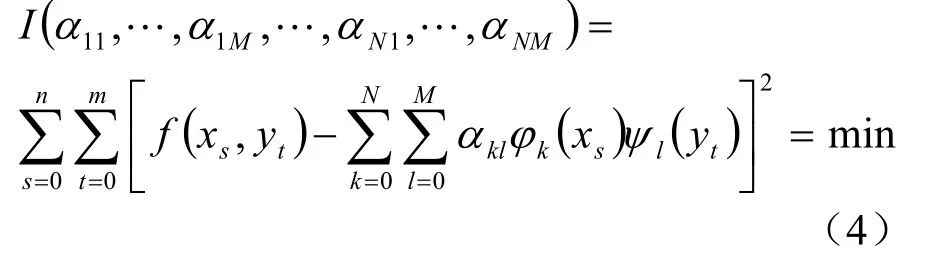
第一步任意固定yt，用Lx表示对函数f(x,y)作x方向的最小二乘拟合，则有

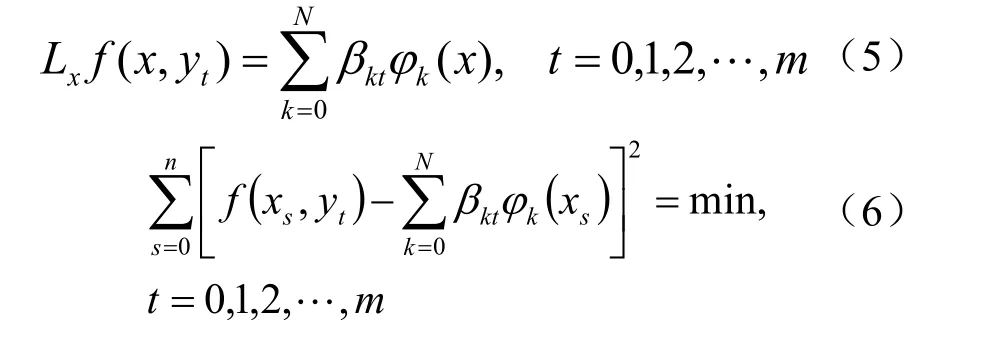
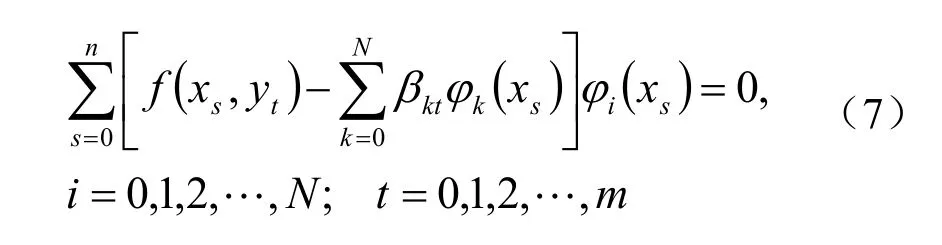
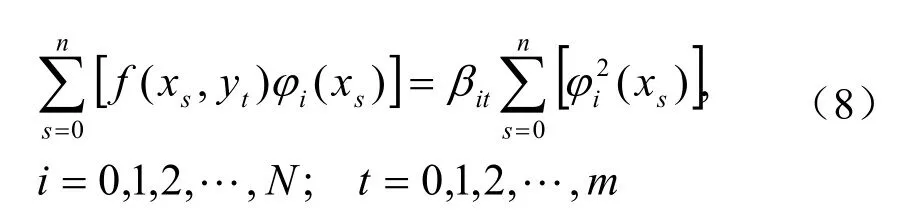
第二步记Ly是y方向的最小二乘拟合，则有

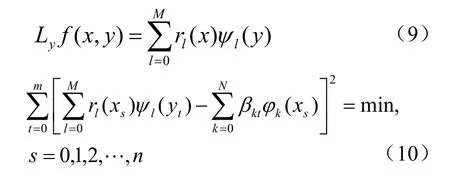
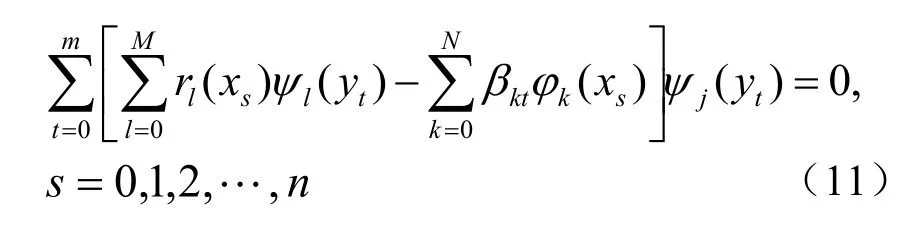
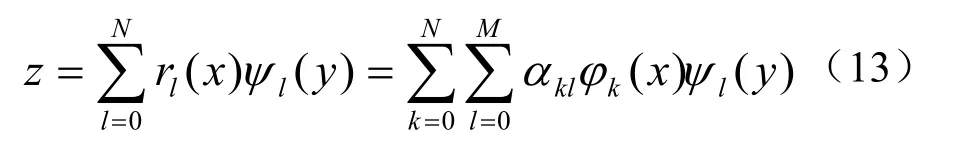
式(4)的一步拟合，N+M一般最高不超过6。分步拟合的每步按一维拟合，对普通多项式N、M最高均可选6。

若采用正交多项式，系数识别式(8)和式(12)不须解方程，因此可采用高于6阶的多项式，可有效提高曲面拟合的精度。

2 正交多项式递推算法[12]

3 数字算例

3.1 边缘拟合

由式(2)可以生成边缘图像如图1，在边缘附近选择一小区域，用乘积型正交多项式对区域内子图像数据进行二维拟合，以采用Canny法确定的整像素边缘位置为中心(x0,y0)，选择n×m（跨边缘为n，沿边缘为m）矩形区域子图像

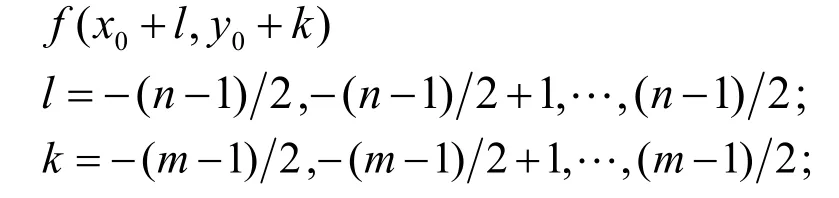
用二维正交多项式对其进行拟合。为分析比较，区域选n×m=21×7，二维多项式选N=6,10,15,20，M=6。图2、图3为拟合结果。

图1 根据高斯边缘模型生成的图像

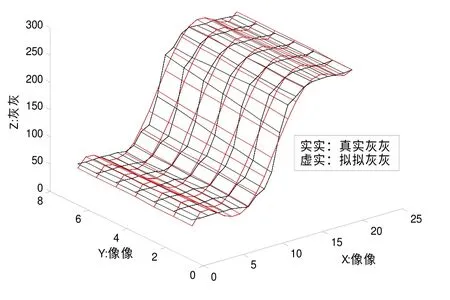
图2 6×6阶二维多项式边缘拟合

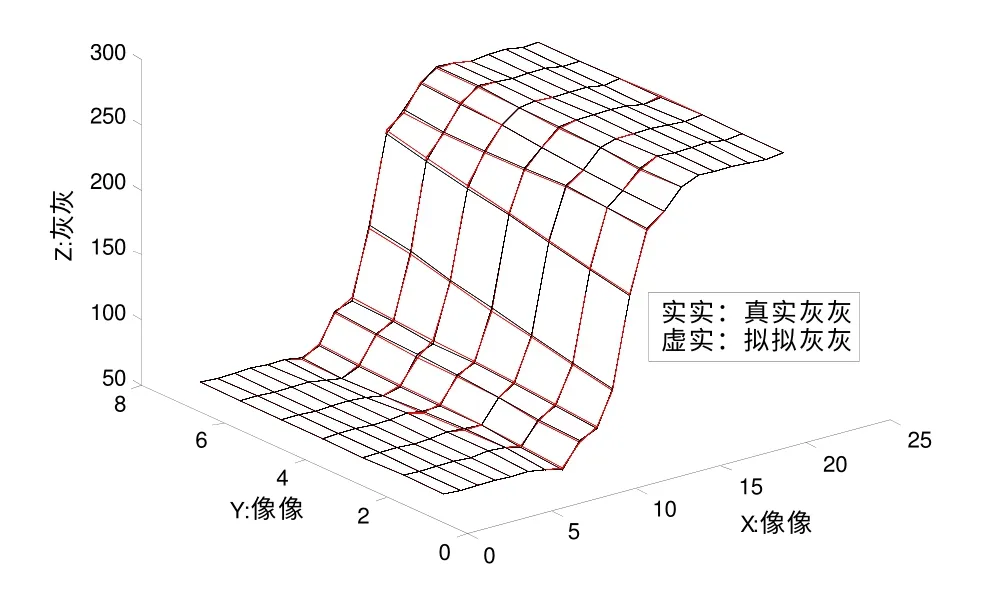
图3 20×6阶二维正交多项式边缘拟合

如前所述，普通多项式拟合阶数最高可选6阶，图2 为普通多项式拟合的最佳结果。跨边缘方向21个数据构成的曲线变化较大，多项式最高可选20阶，选择6～20阶正交多项式进行拟合以进行比较，沿边缘方向，曲线变化较缓，2～6阶多项式拟合效果相差不明显。图3可见高阶正交多项式拟合效果明显优于图2的6阶普通多项式。

3.2 边缘识别

一般认为灰度变化最大的点为边缘位置，可以由灰度曲面方向变化率最大确定边缘的位置，即按梯度确定边缘的位置，这里采用近似的多项式边缘模型，近似采用确定边缘的位置[1]。

以图1为参考图像，给其边缘一竖向3像素位移生成位移图像。先识别两幅图像中边缘曲线，再由这两曲线的差得到边缘的变形。图4为无噪声图像边缘变形识别结果比较，虚线为一维拟合，实线为二维拟合。图5为含5%噪声图像的边缘变形识别比较。一维拟合采用6阶普通多项式[6]，二维拟合采用20×6阶正交多项式。图4可见，二维方法处理无噪声图像，识别边缘位移最大绝对误差0.08像素，相对误差2.7%，略好于一维拟合，多数像素点位移的误差在0.03像素以内。如果采用小波分解或奇异值分解等方法对边缘或变形识别数据进行去噪处理[17]，误差可控制在0.01像素左右。图5可见，对含噪声图像的处理，二维方法识别边缘变形的效果明显优于一维方法。

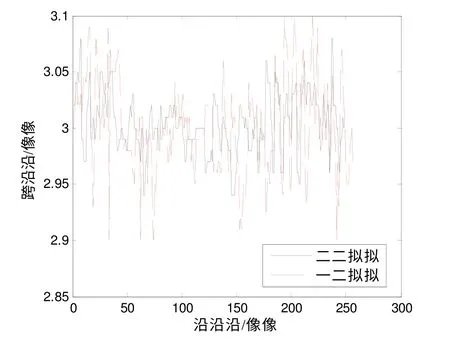
图4 无噪声图像边缘变形识别

图5 5%噪声图像边缘变形识别

4 模型试验

试验模型为铝合金槽形梁，横截面尺寸如图6，壁厚1mm，梁长1366mm，两端用直径25mm的钢锟轴支撑以实现简支，计算跨径l=1341mm，在跨中加载。因为试验主要目的是比较图像检测与传统检测的结果和验证边缘检测的新方法，对荷载未精确控制，未采用高像素高质量摄像器材，采用480×640像素网络摄像头。试验采集图像、边缘检测及变形检测结果，如图7～图9所示。区域选n×m=21×7，二维多项式选N=20，M=6。

图6 槽形梁横截面尺寸(mm)

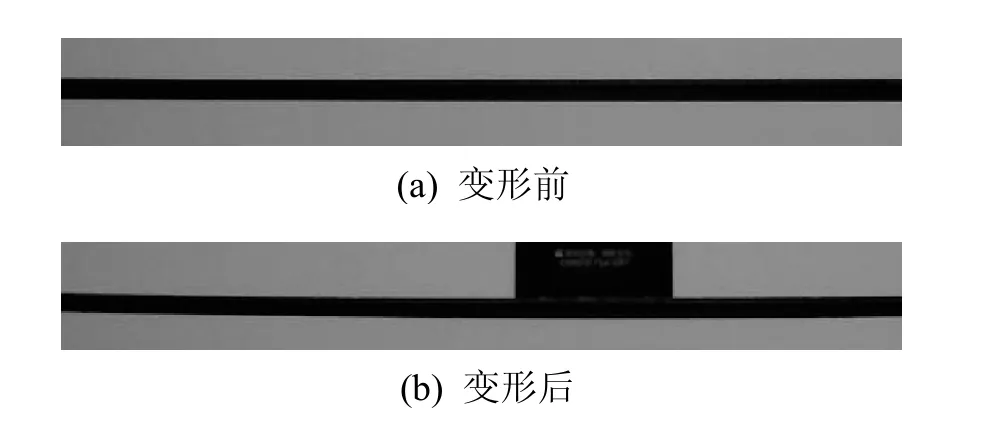
图7 梁变形图像

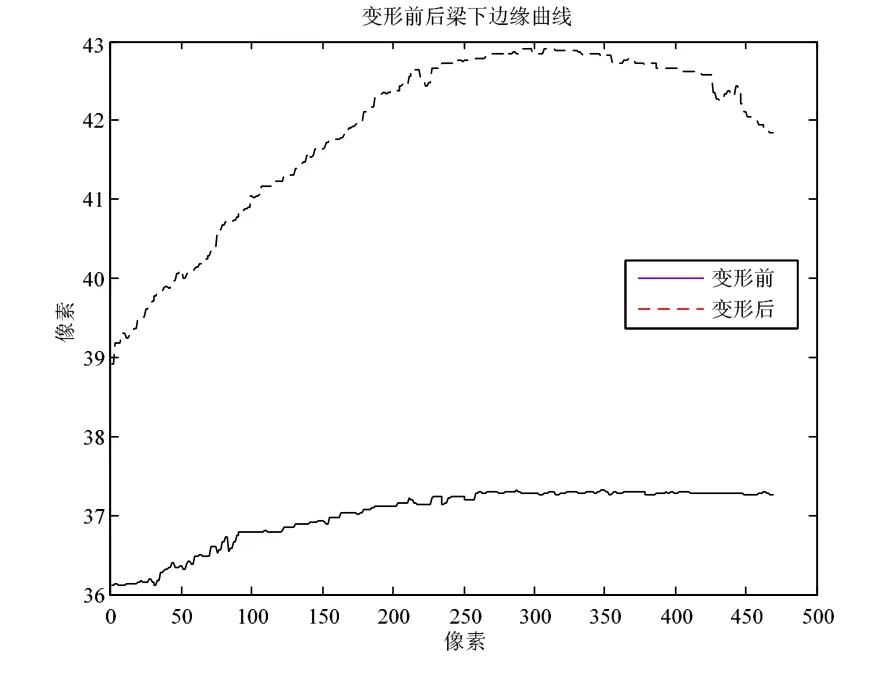
图8 由边缘识别检测所得梁底边缘曲线

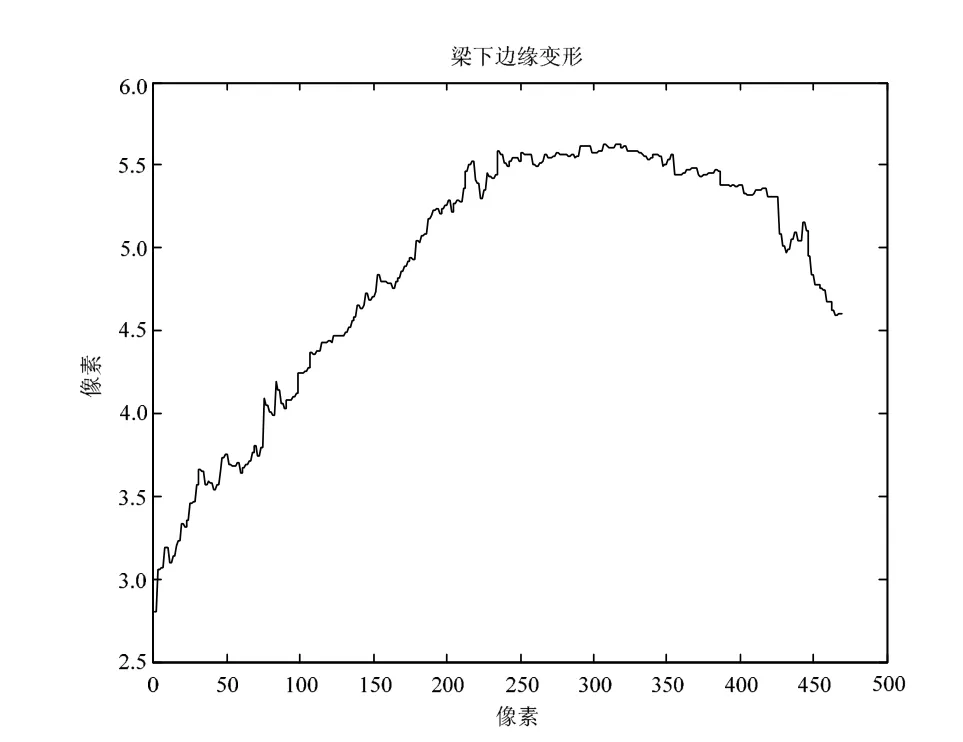
图9 由边缘识别检测所得梁底变形曲线

由图8，图9可见，边缘检测曲线波动范围基本上在±0.05像素之内，边缘变形检测曲线波动范围基本上在±0.1像素之内。说明新方法边缘检测的分辨率和稳定性较高。

按以下过程进行标定将检测结果换算为毫米。由梁的物理尺度与像素尺度比较，可得图像纵横向检测标定系数分别为10mm/11像素和540mm/470像素。由梁跨中检测挠度与理论值比较，得梁的荷载抗弯刚度比P/EJ。简支梁挠度曲线理论解为

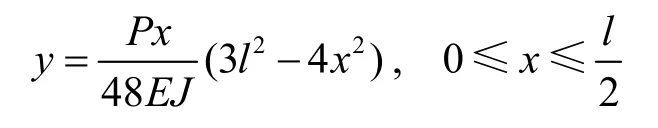
图10为实测值与理论值的比较，两者符合较好。

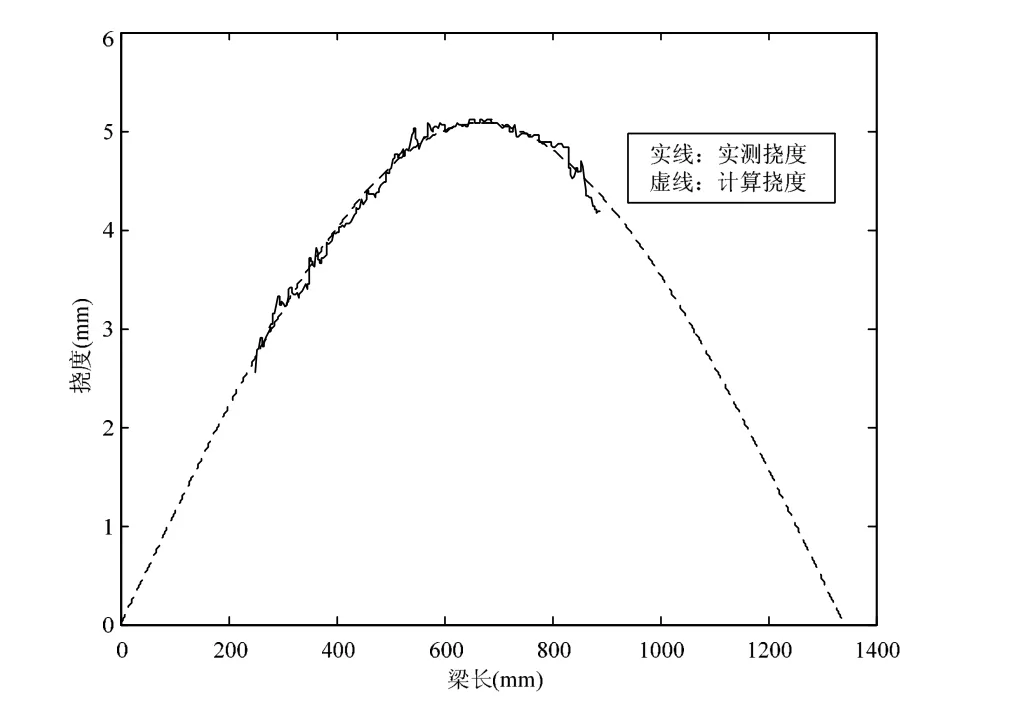
图10 实测值与理论值的比较

5 结 论

（1）边缘检测属二维问题，采用一维方法进行检测局限性明显。现有方法中基于高斯边缘模型拟合方法检测效果最好，但其优化方程是非线性隐式方程，只能用数值方法，6个待定参数的隐式方程中含有反常积分，算法较复杂。多项式拟合法，优化方程是显式线性方程，算法简单易行，但高于6阶的多项式不能提高拟合效果，用于一维拟合还可以，二维拟合一个方向用2阶，另一个方向最高只能用4阶，无法满足边缘拟合的要求。采用分步拟合，两个方向均可为6阶。正交多项式二维拟合法，参数识别的优化过程不用求逆或解方程组，可以在采用高阶多项式，对于n×m的子图像，最高可采用(n-1)×(m-1)阶多项式，多项式的阶数只取决于子图像的尺度，保证较好的拟合效果。拟合过程只须算术除法，算法简易。

（2）对生成图像进行边缘检测的结果表明，适当提高多项式阶数可以提高拟合效果，二维正交多项式法检测效果优于一维普通多项式的检测，对于含噪声图像的检测新方法的效果更明显。

（3）简支梁模型试验表明，变形前后梁底检测边缘曲线波动较小，说明检测方法稳定性分辨率较高，由这两条曲线的差所得的梁变形曲线波动较小，说明二维拟合对由于梁弯曲引起的边缘横向变化的适应性较好，这也是二维拟合优于一维拟合的原因。检测变形的波动范围多数在±0.1像素之内，如果对若干像素点取平均，其精度可提高到±0.02像素左右，亚像素变形检测的效果明显。以30万像素（640×480）网络摄像头采集约1.2m范围内梁的变形图像，边缘识别所得变形检测精度与百分表检测结果相当。

（4）一维拟合法，对各边缘点跨边缘N个像素点一次拟合即可。二维分步拟合法，对M个像素的一小段边缘，先进行M次拟合（对N个像素点拟合）形成中间数据，再对中间数据进行N次拟合（对M个像素点拟合），因此相对于一维拟合增加了极大的计算量。相对于普通多项式拟合，正交多项式增加了递推计算，拟合区间和多项式阶数的增加，均会导致计算量的增加。

（5）本文方法适用于直边、平滑曲边构件的边缘识别和变形检测。

[1]章毓晋.图像工程(中册)图像分析(第2版)[M].北京:清华大学出版社,2006: 75-156.

[2]Tabatabai A J,Mitchell O R.Edge location to sub-pixel values in digital imagery [J].IEEE-PAMI,1984,6(2): 188-201.

[3]Nalwa V S,Binford T O.On detecting edge [J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1986,8(6): 699-714.

[4]Steger C.Unbiased extraction of curvilinear structures from 2D and 3D images [D].Dissertation of PhD,Germany: Technischen Universitat Munchen,1998.

[5]袁向荣.梁变形检测的一维数字图像相关法[J].广州大学学报(自然科学版),2010,9(1): 54-56.

[6]Fu G K,Moosa A G.An optical approach to structural displacement measurement and its application [J].Engineering Mechanics,2002,128(5): 511-520.

[7]Yuan Xiangrong.Polynomial moving fitting method for edge identification [J].Advanced Material Research,2011: 308-310,2560-2564.

[8]Yuan Xiangrong.Digital image edge detection method in the application of the beam displacement measurement and damage detection [J].Advanced Materials Research,2012,487: 221-225.

[9]Yuan Xiangrong.The natural bending vibration of the continuous beam and the impact factor of bridge [J].Applied Mechanics and Materials,2011: 90-93,1245-1249.

[10]黄 文,袁向荣.视频图像振动测试技术研究[J].微型机与应用,2011,30(22): 62-64.

[11]刘 敏.数字图像处理技术在桥梁结构检测中的应用研究[D].广州: 广州大学土木工程学院,2009.

[12]徐士良.数值方法与计算机实现[M].北京: 清华大学出版社,2010: 257-274.

[13]Ye J,Fu G,Poudel U P.High-accuracy edge detection with blurred edge model [J].Image &Vision Computing,2005,23(5): 453-467.

[14]Shan Y,Boon G W.Sub-pixel location of edges with non-uniform blurring: a finite closed-form approach [J].Image and Vision Computing,2000,18(13):1015-1023.

[15]Elder J H,Zucker S W.Local scale control for edge detection and blur estimation [J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1998,20(7): 699-716.

[16]黄友谦.曲线曲面的数值表示和逼近[M].上海:上海科学技术出版社,1984: 137-147.

[17]胡朝辉,袁向荣,刘 敏.简支梁位移场小波去噪的试验研究[J].广州大学学报(自然科学版),2010,9(6): 50-53.