基于二次代数曲线端点几何信息的最优有理参数化

厉玉蓉， 姜 丽

（1.山东工商学院计算机科学与技术学院，山东 烟台 264005；2.山东师范大学信息科学与工程学院，山东 济南 250014）

曲线、曲面是计算机图形学(CG)和计算机辅助几何设计(CAGD)中的基本研究对象。参数曲线曲面具有构造简单直观、易于显示等特点，又脱离了对坐标系的依赖，因而在计算机图形学中得到广泛应用。在图形的显示过程中，参数化算法的优劣会直接影响曲线段的绘制效果。二次代数曲线的参数化的数学实现并不困难，但仅仅是实现还远远不能满足工程需要，一方面，在实际的应用中，往往需要对曲线的某一部分进行参数化，而不是整条曲线；另一方面，出于工程需求、造型美观和计算量等方面的考虑，工程人员往往想要得到曲线的最优参数化方程[1-7]。

理论上来说，弧长参数化是理想中最优的参数化。代数曲线的弧长参数化不可能是有理参数化方程，而有理参数化是最常用的一种参数化形式，因此众多学者转为研究最接近弧长参数化的有理参数化方程[8-11]。

最优参数化的评判标准对最优参数化的构造具有一定程度的影响。Rida[9]提出了一个评判标准，并利用这一标准得到了一类曲线参数化方程。但是该评判标准存在一定的不足：曲线几何信息不明确、不能确定该类参数化所能达到的最优值。从物理意义讲，在参数域[0,1]上，可以将参数看作时间，曲线上某点的切向量的模看作该点处的移动速率，则曲线上各个动点的移动速率的波动越小越好，若保持均匀，则可弧长参数化。

本文利用文献[10]中的评判标准来衡量参数化效果的优劣，这一标准可以简单的表述为参数曲线切矢量模的最大值和最小值的比与1的接近程度。

1 二次代数曲线的最优有理参数化

1.1 问题描述

设g(x,y)∈R[x,y]是关于x,y的二次多项式，方程g(x,y)=0定义了一条平面二次代数曲线C。A、B分别是曲线C上的两个点，向量n0为A点的单位切向量，求以A为起点，沿n0方向到达B点的曲线段的最优有理参数化。

不妨设A=(0,0),B=(x1,y1),n0=(n0x,n0y)=(1,0)，否则可通过平移、旋转变换使其满足。记向量n1=(nx,ny)为B点的单位切向量，曲线在A点处的曲率半径为ρ，不失一般性，令曲线段AB的参数域为[0,1]，如图1所示。

图1 参数域为[0,1]的曲线段AB

1.2 有理参数化及最优评判标准

对于二次曲线：

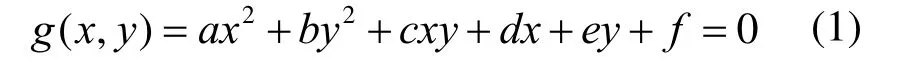
由于曲线过点A(0,0)，且与x轴相切，则有：

依照文献[10]的方法可得曲线段AB对应于参数域[0,1]的所有二次有理参数方程：

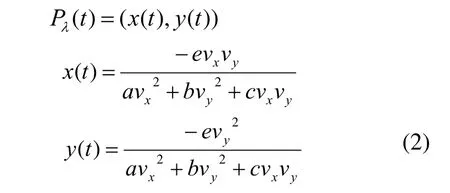
其中

λ为非零实数。

(t)=(x′(t),y′(t))是参数曲线Pλ(t)的切矢量，记

如果Γ(P*)=min{Γ(P(t))}称此P*(t)为曲线段AB的最优参数化方程。显然

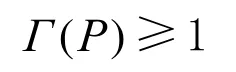
Γ(P)=1⇔P(t)可弧长参数化。

注意，对于代数曲线的有理参数化方程必有Γ(P)＞1。

1.3 参数λ的确立

定理对于二次曲线段有理参数化，曲线切矢量的模的值在起点和终点处相同的充分必要条件是λ=（其中l是线段AB的长度，ρ表示代数曲线C在起点A处的曲率半径，α表示向量n1和直线AB的夹角）。

证明：

必要性：

首先利用曲线段的几何信息确定其代数方程：

设l1、l2、l0分别为三条二次曲线起点处切向量、终点处切向量和由起点指向终点的向量所在的直线（如图1所示），直线方程分别为：

l1:y=0

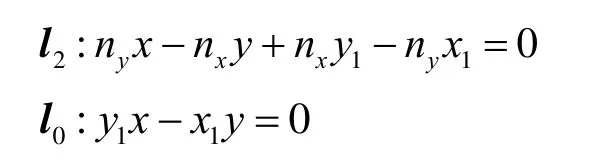
根据文献[11]利用二次曲线的几何信息，任意经过A、B两点，且分别以l1,l2为切线的二次曲线可以表示为如下形式：

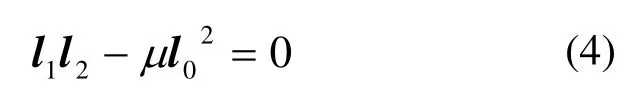
其中，μ为自由参数，可由曲线起点处的曲率半径确定。

分别将l0,l1,l2的直线方程代入式(4)得二次曲线的代数方程为：

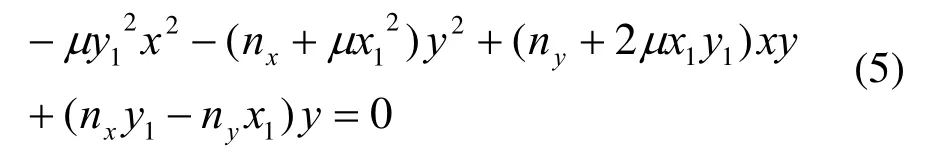
对比方程(1)，(5)可求得二次曲线的系数：

由曲线起点处的曲率半径ρ可确定参数μ为：

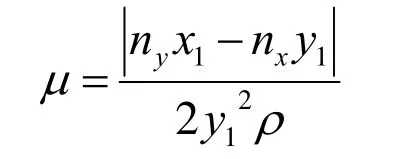
由公式(2)，(6)二次有理参数方程可表达为：

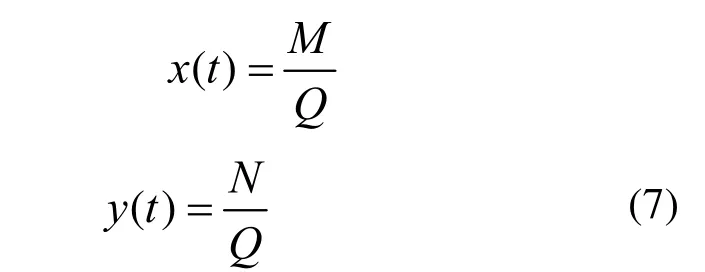
其中：

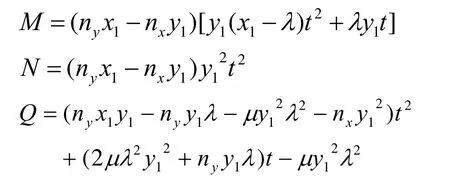
由于曲线C的参数速率在起点和终点处相同，即：

利用式(7)并分别求出x′(0)，y′(0)，x′(1)，y′(1)，代入式(8)化简得到：

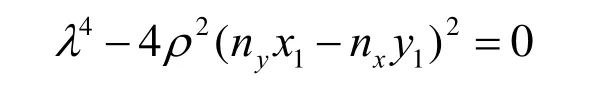
根据λ的几何意义，舍去负根求得：

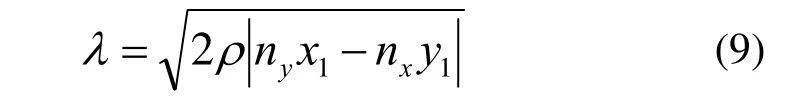
其中

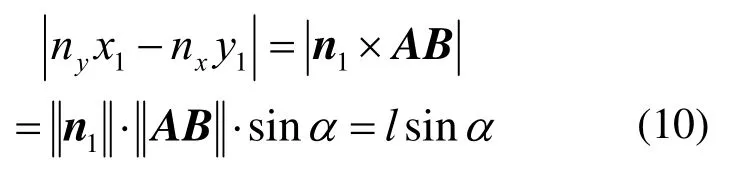
将式(10)代入式(9)得λ=

充分性：

将λ=代入公式(2)易求：

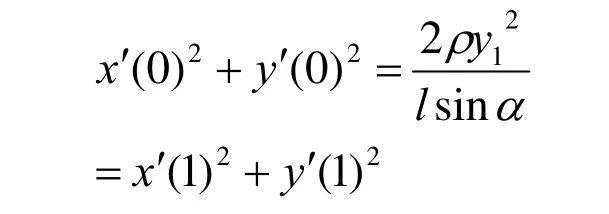
即曲线端点处切矢量的模相等。 证毕！

由于AB曲线段对应[0,1]参数域的有理参数方程可由公式(2)给出，λ是其自由参数，即Γ值由λ决定，则寻求最优有理参数方程即是寻求使得Γ值最小的λ。Γ值是参数速率的最大值与最小值的比，大量实例表明，若存在二次曲线段的有理参数方程Pλ(t)满足且是最值，则此参数化即为最优有理参数化。此时的λ可由定理给出的公式来构造并确定。

2 实例分析

2.1 实例1

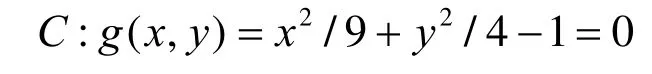
已知平面二次代数曲线：上点A(3,0)和B(0,2)，按逆时针方向求AB弧的最优有理参数化。

用本文方法有理参数化时得到曲线段AB的参数方程：

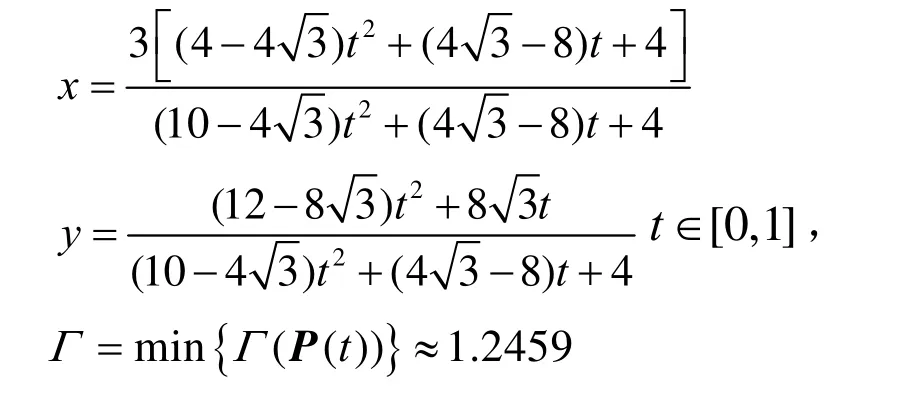
本文方法参数化后的曲线及曲线的参数速度分别如图2中的空心点和图3中的实线所示，得到的是曲线段的最优有理参数化方程。文献[10]的方法参数化后的曲线及曲线的参数速度分别如图2中的实心点和图3中的虚线所示,此时Γ≈1.6204。

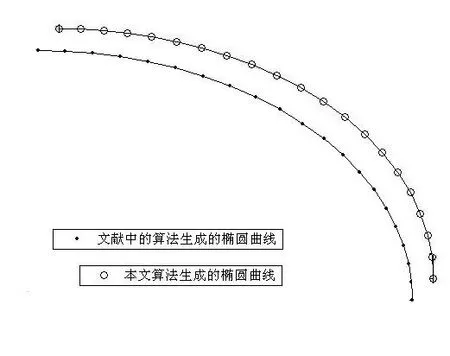
图2 1/4椭圆弧的参数化对比效果图

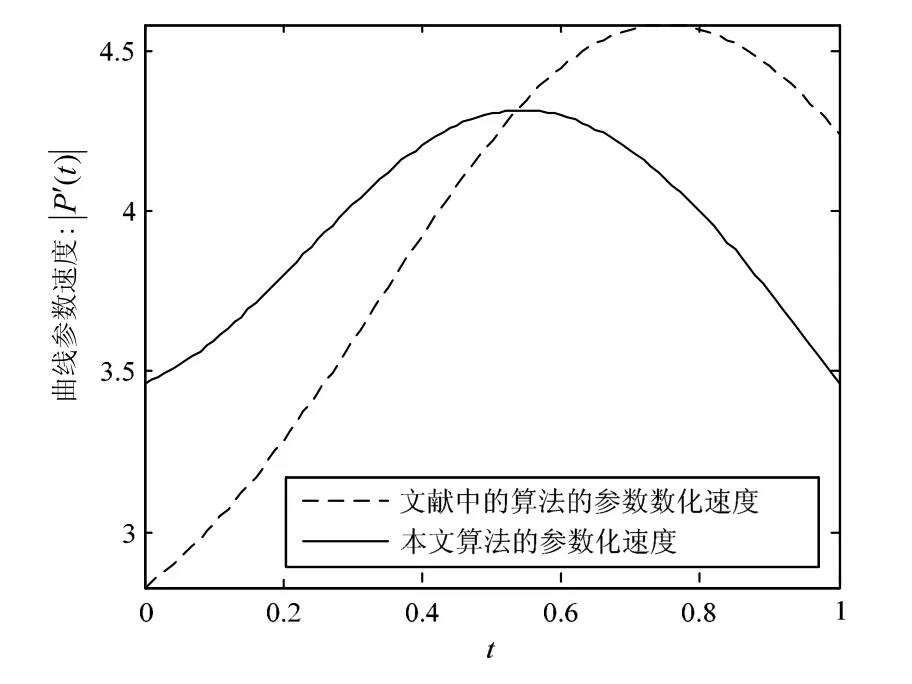
图3 1/4椭圆弧的参数速度对比效果图

2.2 实例2

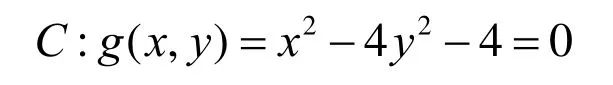
已知平面二次代数曲线上点A(2,0)和点B(4,)，按逆时针方向求AB弧的最优有理参数化。

用本文方法有理参数化时得到曲线段AB的参数方程：

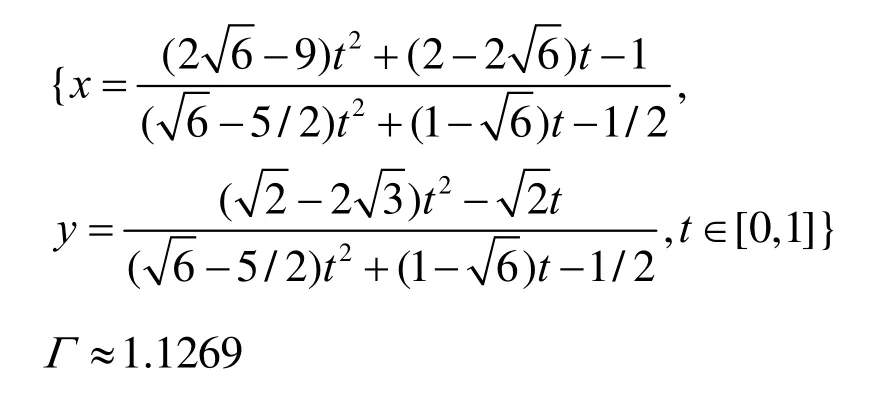
本文方法参数化后的曲线及曲线的参数速度分别如图4中的空心点和图5中的实线所示。最优的Γ值约为1.1265，本文方法得到的是曲线段的逼近最优的有理参数化方程。文献[10]的方法参数化后的曲线及曲线的参数速度分别如图4中的实心点和图5中的虚线所示，此时Γ=4.0000。

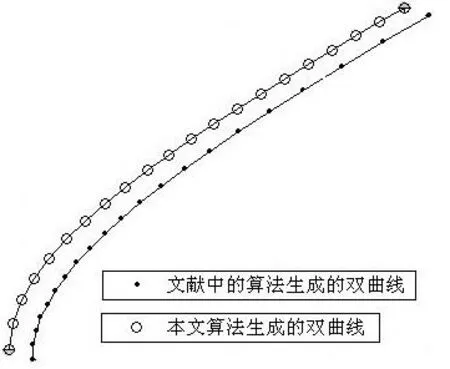
图4 双曲线弧的参数化对比效果图

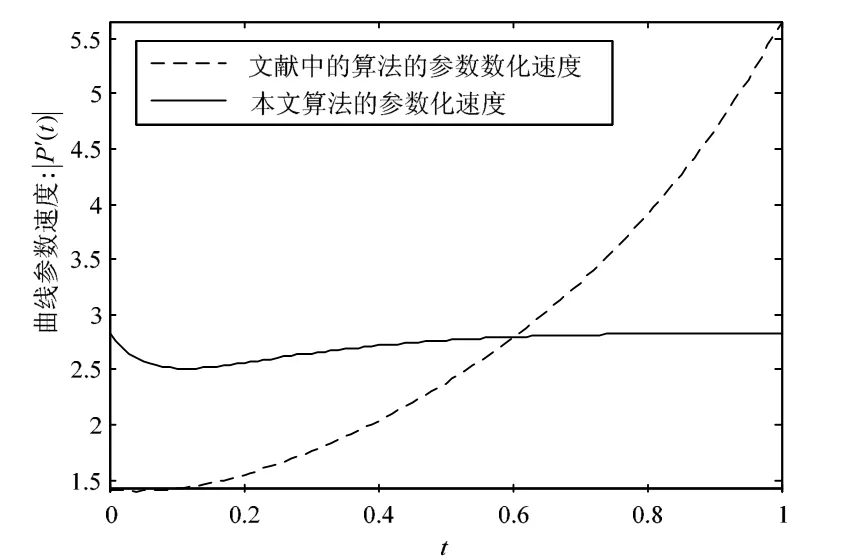
图5 双曲线弧的参数速度对比效果图

表1给出了更多实例结果。

3 结束语

理论上，最优有理参数化方程可求，但是计算量非常大，对于任意的二次代数曲线，本文根据端点处参数速率相等来直接构造出有理参数化公式，实例也显示了方法的有效性。对于一段圆弧，椭圆或双曲线上的具有对称性质部分的有理参数化，用本文方法得到的就是最优有理参数化；若参数化曲线段端点处的参数速率相等且是最值，实验数据显示也是最优的；另外，其他情形非常逼近于最优。

本文仅对二次代数曲线进行了最优参数化研究，下一步的研究工作将针对三次或者高次代数曲线最优有理参数化展开，对于Γ值偏大的曲线如何选择分段方法以达到接近弧长的参数化也是值得研究的。

表1 部分实例结果与最优参数化和文献参数化的对比

[1]Abhyakar S S,Bajaj C.Automatic parameterization of rational curves and surfaces III: Algebraic plane curves [J].Computer Aided Geometric Design,1988,5: 309-321.

[2]Sonia P D,Sendra J R,Sonia L R,Sendra J.Approximate parametrization of plane algebraic curves by linear systems of curves [J].Computer Aided Geometric Design,2010,27(2): 212-231.

[3]Sonia P D,Sendra J,Sendra J R.Parametrization of approximate algebraic curves by lines [J].Theoretical Computer Science,2004,315(2): 627-650.

[4]Kuznetsov E B.Optimal parametrization in numerical construction of curve [J].Journal of the Franklin Institute,2007,344(5): 658-671.

[5]Hartmann E .Numerical parameterization of curves and surfaces [J].Computer Aided Geometric Design,2000,17(3): 251-266.

[6]厉玉蓉,张彩明.三角网格上的代数曲面重建[J].计算机辅助设计与图形学学报,2007,19(4): 460-463.

[7]Zhao Xiuyang,Zhang Caiming,Yang Bo,Li Pingping.Adaptive knot placement using a GMM-based continuous optimizationalgorithm in B-spline curve approximation [J].Computer-Aided Design,2011,43(6): 598-604.

[8]郭凤华.参数曲线的最优参数化[J].计算机辅助设计与图形学学报,2007,19(4): 464-467.

[9]Rida T F.Optimal parameterizations [J].Computer Aided Geometric Design,1997,(14): 153-168.

[10]厉玉蓉,胡芳刚.平面二次代数曲线的最优参数化[J].图学学报,2012,33(2): 49-52.

[11]张三元.基于代数曲线段的G2连续的曲线造型方法[J].计算机学报,2000,23(2): 153-157.