周期系数线性系统的稳定性

李 迪,熊良林,和晓萍,程碧辉

(云南民族大学 数学与计算机科学学院,云南 昆明 650500)

线性时变周期系统在科学研究与实际工程问题中经常出现,物理和工程技术中有许多问题最终也都能转化为具有周期系数的线性微分方程组.用非线性微分方程组描述的周期运动,许多实际方法也是围绕研究带有周期系数的线性微分方程[1]来讨论的，故周期系数线性方程组稳定性的研究具有重要意义.而在周期系数线性系统中,周期系数情形起着非常重要的作用.

目前,线性时变周期系统的稳定性在很多文献中都作了深入研究[2-3], 而本文的目的, 在于从周期系数线性系统的系数矩阵入手, 在文献[1]的基础上,对周期系统中的矩阵的稳定性进行改进,我们的思想是把矩阵稳定的条件减弱为拟稳定,结果得到相应的周期系统的平凡解由指数稳定变为了稳定的判据.该判据比原有判据所涉及的情形更普遍,也更具有适用性.最后,本文使用仿真例子对所给判据进行验证.

1 预备知识

本文主要考虑具有周期系数的线性系统[1]:

(1)

其中x∈Rn为状态向量,A(t)∈Rn×n,A(t+T)=A(t).

为了后面结论的推导与证明方便,特引入如下定义与引理：

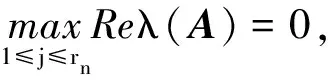
引理1[1]系统(1)的平凡解稳定的充要条件是它的Cauchy矩阵K(t,t0)(t≥t0)有界.

引理2[4]X(t)=X(kT+t1)=

X((k-1)T+t1+T)=X((k-1)T+t1)X(T)=

X((k-2)T+t1+2T)=X((k-2)T+t1).

X2(T)=…=X(t1)Xk(T) .

(2)

2 主要结果

本文在文献[1]的基础上,对周期系统中的矩阵的稳定性进行改进,放宽条件为拟稳定,得到当矩阵拟稳定时,周期系统平凡解稳定性的判据.下面在给出几类特殊的周期系数线性系统的稳定性[2-3]判据之前, 引入如下表示:

定理1 若周期系数系统式(1)满足:

1)A(t)∈μ*:={A(t)|W(1)(t)≡0,∀t};

则式(1)的平凡解稳定.

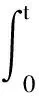
设t∈[kT,(k+1)T],t=kT+t1,由(2)式可知:

X(t)=X(t1)Xk(T)=X(t1)ek(B(T)-B(0)).

(3)

由(3)式及条件2)知,存在常数M>0,使得:

故式(1)的Cauchy矩阵有界,再根据引理1,可得式(1)平凡解稳定.证毕.

定理2 若周期系数系统式(1)满足:

1)A(t)∈μ**:={A(t)|W(1)(t)≠0,W(2)(t)≡0,∀t};

则式(1)平凡解稳定.

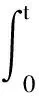
(4)

(5)

的Cauchy矩阵,由于W(1)(t)∈μ*,故:

(6)

由条件3)及式(4),式(5),有:

因为W(1)(t)是以T为周期的周期函数,故以下证明类似于定理1的证明,证毕.

定理3 若周期系数系统式(1)满足定理2的条件1),2),且满足:

则式(1)平凡解稳定.

故式(1)的Cauchy矩阵有界,由引理1 ,可知式(1)平凡解稳定.证毕.

定理4 若周期系数系统式(1)满足:

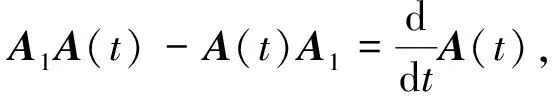
2)A2:=e-A1t0[A(t0)-A1]exp(A1t0),A1A2=A2A1;

3)矩阵A1+A2拟稳定；

则式(1)平凡解稳定.

证明对于等式：

(7)

左乘以e-A1(t-t0),右乘以eA1(t-t0)得:e-A1(t-t0)A1A(t)eA1(t-t0)-e-A1(t-t0)A(t)A1eA1(t-t0)=

A(t)=eA1(t-t0)A(t0)e-A1(t-t0).

(8)

再作变换:x(t)=eA1(t0)y(t),可得:

故有:x(t)=eA1teA2(t-t0)e-A1t0x(t0) .

(9)

从而式(1)的Cauchy矩阵为:x(t)=eA1teA2t=e(A1+A2)t

因为矩阵A1+A2拟稳定,故存在常数M>0,使得:

再由引理1 ,故该定理的结论成立.证毕.

定理5 若周期系数系统式(1)满足:

1)定理4的条件1)、2成立；

2)矩阵A1和A2=e-A1t0[A(t0)-A1]eA1t0拟稳定；

则式(1)平凡解稳定.

证明由定理4的式(7)、(8)、(9),有式(1)的Cauchy矩阵为:

x(t)=eA1teA2t=e(A1+A2)t.

因为矩阵A1和A2=e-A1t0[A(t0)-A1]eA1t0拟稳定,故存在常数M1>0,M2>0,使得:

故式(1)的Cauchy矩阵有界,再根据引理1,可得式(1)平凡解稳定.证毕.

以上5个定理,是在文献[1]的基础上,将相关条件由稳定放宽为拟稳定得到的结论，从而扩展了周期系数线性系统的理论成果.在下一节的数值仿真实例中,将验证所得结果的时效性.

3 数值实例

为了验证定理的时效性,特给出如下仿真例子予以说明:

例1 判定下列系统的稳定性:

证明显然该系统的系数矩阵:

因为Reλ(B(2π)-B(0))≤0,由定义[1]知矩阵B(2π)-B(0)是拟稳定的,故此周期系统是稳定的.给定初始条件x(0)=[-10,25],利用Matlab仿真,可得到系统状态运行图(图1)和系统相图(图2).

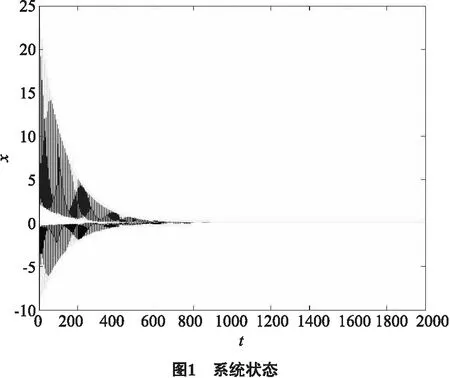
由仿真图1和图2可以看出,在给定初始条件时,所给周期系统是稳定的,从而验证了本文结论的有效性.

4 结论

将矩阵稳定的条件放宽为拟稳定后,通过计算系统的柯西矩阵并讨论其有界性,得到了一系列相关的稳定性结论.从最后的仿真实例可以看出,结论具有一定的可行性.

参考文献:

[1] 廖晓忻.稳定性的理论、方法和应用[M].2版.武汉:华中科技大学出版社,2010,37-41.

[2] MONTAGNIER P,SPITERI R J,ANGELES J .The control of linear time-periodic systems using Floquet-Lyapunov theory[J].International Journal of Control,2004,77:472-490.

[3] BALAS M J,YUNG J L.Controller design of linear periodic time-varying systems[C]//American Control Conference.USA：Albuquerque,1997,5:2667-2671.

[4] 张劲夫,余跃庆.考虑运动副间隙的曲柄滑块机构运动稳定性研究[J].机械科学与技术,2004,23(4):533-5361.