具有一般激活函数的变时滞并联限制细胞神经网络的全局稳定性

贾玉生，杨 红

(青岛滨海学院 文理基础学院，山东 青岛 266555 )

Chua等[1]在1988年首先提出细胞神经网络的相关理论，目前有很多学者研究其理论和应用[2-12]，细胞非线性网络是当今计算机科学、电子工程、数学、信息科学等学科和领域的研究热点之一，神经网络模型在人工智能、认知科学、生物分子学等领域有广泛应用，1991年美国学者Pinter教授等[2]首先提出并联限制细胞神经网络(SICNNs),从那时开始，很多学者研究了并联限制细胞神经网络，现在它在数据压缩、模糊信息处理、图像处理及优化设计等众多领域有广泛应用.考虑的时滞并联限制细胞神经网络的初始模型如下：cij表示在(i,j)位置的细胞，其在t时刻的状态方程为：

(1)

其中xij(t)是细胞cij在t时刻的活动状态函数，Lij(t)表示外部输入函数，激活函数f(xkl)是连续函数且是正的，Nr(i,j)是细胞cij的一个r-邻域：

Nr(i,j)={ckl:max(|k-i|,|l-j|≤r,1≤k≤m,1≤l≤n}.

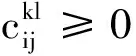
从神经网络现有的实际应用出发，其收敛的动力学行为研究的较多，人们总认为动力学行为最终获得的信息是抓得住的形式，既稳定状态的平衡点，这种稳定状态的获取在模式识别、组合优化等方面很有用，如果我们利用的神经网络模型是稳定的，则我们的目的比较容易达到，所以在神经网络的设计和分析中，系统的稳定性分析是极为重要的且是非常有实际意义的.

另一方面，在实际模型的设计时,需要考虑一些重要数据的变化范围和重要的系统参数的取值界限,比如在电路设计中，系统参数的扰动是必须要考虑的具体问题，因此，研究系统在参数的某些变化内的稳定性也就是系统的鲁棒稳定性是非常重要的，我们研究如下的并联限制细胞神经网络系统

(2)

其中，τ是一个有界非负常数，f(xkl)是连续的函数且是正的、有界的，根据实际情况，在文中我们研究Lij(t)=Lij为常数的情况，根据激活函数的实际意义，研究并联限制细胞神经网络时有假设H1：

|f(x)-f(y)|≤μ|x-y|.

文献[13]给出了系统(2)的一个与时滞无关的全局鲁棒稳定性的充分条件，

在实际的网络应用时时滞往往不是固定的而是随时间变化的，应该说常时滞仅为变时滞的特殊情况，所以我们研究变时滞并联限制细胞神经网络的全局稳定性更具实际意义.

考虑变时滞并联限制细胞神经网络系统

(3)

其中，根据实际情况我们认为τ(t)是非负有界的连续函数，即存在正数τ>0，0≤τ(t)≤τ，在文中我们研究Lij(t)=Lij为常数的情况，在以往的研究中[9-10,14]，都是假设f(xkl)是正的连续有界函数，这在某种程度上限制了实际应用，而我们研究具有一般激活函数的情形，我们仅要求If=infx∈Rf(x)存在即可, 这是比较新的尝试，我们研究并且得到了其全局稳定的充分条件.

1 主要结果

下面给出具一般激活函数的变时滞并联限制细胞神经网络的全局稳定性的充分条件.

定理1 若x*是系统(3)的平衡点，当假设H2:

成立时，则

证明若x*是系统(3)的平衡点，则x*满足

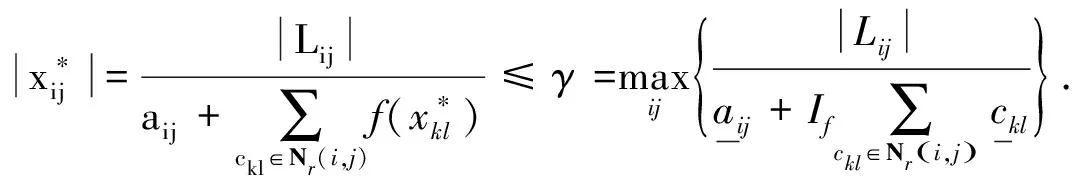
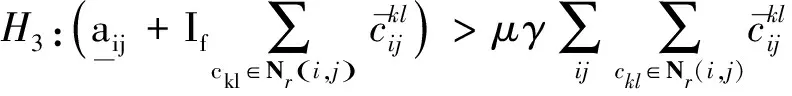
成立，则系统(3)存在唯一的平衡点.

证明假设x=x*是系统(3)的平衡点，那么满足

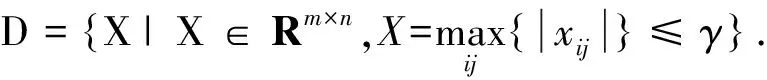
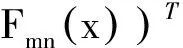
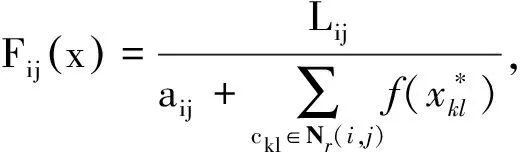
所以映射F是映射D到D的连续自映射，由Brouwer不动点定理知映射在D上至少存在一个不动点x=x*，从而系统(3)至少有1个平衡点.

又对任意的X,Y∈D, 有

由H3显然可得0<λ<1，所以映射F为压缩映射，由压缩映射原理知存在唯一的x*满足F(x*)=x*，因此，系统(3)有唯一的平衡点.

定理3 假设H4：τ(t)可微,且存在正数τ>0，使得0≤τ(t)≤τ，1≥1-τ′(t)≥ζ>0，有

成立，则系统(3)的平衡点是全局鲁棒稳定的，其中γ如引理1所规定.

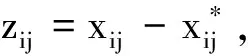
(4)

要证明定理3，只要证明系统(4)的平衡点是全局鲁棒稳定的即可.

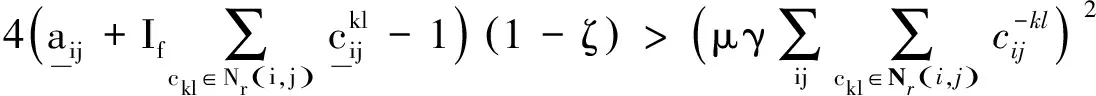
由Lypounov稳定性理论知系统(4)的平衡点是全局鲁棒稳定的,所以系统(3)的稳定点是全局鲁棒稳定的，即定理成立.

推论1 若τ(t)=τ为常数，且假设H1,H2,H3,H4成立，则系统(3)的平衡点是全局鲁棒稳定的.

2 结语

研究了具有一般激活函数的变时滞并联限制细胞神经网络的全局稳定性，这是一个比较新的尝试，并且给出了全局鲁棒稳定的一个充分条件，为其应用提供了更为广泛的理论依据.

参考文献:

[1] CHUA L O, YANG L.Cellular neural networks: Theory[J].IEEE Trans Circuits Syst，1988，35(10)： 1257-1272.

[2] BOUZERDOUM A, PINTER R B.Shunting inhibitory cellular neural networks: derivation and stability analysis[J].IEEE Trans Circuits Systems I Fund Theory and Appl,1991,40(3)：215-221.

[3] KELLY D G.Stability in contractive nonlinear neural networks[J].IEEE Trans.Biomed, 1990, 37 (3): 231-242.

[4] KOHONEN T.Self-organization and Associative Memory[M].NewYork：Springer, 1988

[5] LI J H，MICHEL A N, POROD W.Qualitatie analysis of a class of neural networks[J].IEEE Trans Circuits Syst，1998,35:976-986.

[6] WEI Jun-jie,RUAN Shi-gui.Stability and bifurcation in a neural network model with two delays[J].Phisica D, 1999, 130:255-272.

[7] LIAO X X.Math theory (I) of cellular neural networks[J].Science China：Series A,1994, 24 (9):902-910.

[8] LIAO X X.Math theory (II) of cellular neural networks[J].Science China：Series A, 1994, 24 (10):1037-1046.

[9] ROSKA T, WU C W, CHUA L O.Stability of cellular neural networks with dominant nonlinear and delay-type template[J].IEEE Trans Circuits and Systems I: Fundamental Theory and Applications,1993,40 (4):270-273.

[10] LI Yong-kun, LIU Chun-chao, ZHU Li-fei.Global exponential stability of periodic solution for shunting inhibitory CNNs with delays[J].Physics Letters A, 2005,337,46-54

[11] ZHOU Dong-ming, CAO Jin-de.Globally exponential stability conditions for cellular neural network with time varying delays [J].Applied Mathematics and Computation, 2002,131, 487- 496.

[12] 余昌勤.一种基于NSCT变换的RBF神经网络自适应阈值去噪方法[J].云南民族大学学报：自然科学版，2013，22(4)：295-298.

[13] WANG Ling-na, LIN Yi-ping.Global robust stability for shunting inhibitory CNNs with delays [J].International Journal of Neural Systems, 2004,14(4):229-235.