L-BFGS法时间域全波形反演中初始矩阵的选择方法
王 义,董良国
(同济大学海洋地质国家重点实验室,上海 200092)
地震全波形反演(full waveform inversion,FWI)是近年来勘探地球物理领域的研究热点之一。它利用叠前地震记录的波形信息来重建高精度的地下介质的物性参数(密度、速度和模量等),可以为油气勘探中的偏移成像提供更精确的背景速度[1],可以应用到储层定量研究领域[2],还可以应用到全球局部和区域地壳和上地幔结构等研究中[3]。因而,在油气勘探开发和地球动力学等领域有着广阔的应用前景。
20世纪80年代,Lailly[4]和Tarantola[5]利用最小二乘优化的思想在时间域建立了FWI的核心框架。FWI希望找到最优的地下介质模型参数,使模拟地震记录与观测记录达到最佳匹配。FWI涉及的数据量大、模型参数多,是典型的大规模优化问题,通常采用局部迭代优化方法求解[6]。目标函数对模型参数的二阶导数,即Hessian矩阵,对加速迭代方法的收敛起着重要作用[7]。但巨大的计算和存储消耗使显式获取Hessian及其逆矩阵变得非常困难。克服这个困难通常有三类方法:预条件共轭梯度法(preconditioned conjugate gradient method,PCG)、不精确Newton法和拟Newton法[6]。PCG法在FWI中获得了大量应用[8],它通过使用预条件矩阵对梯度进行校正,来加速迭代的收敛过程[9-13]。而预条件矩阵通常是先对Hessian矩阵做一些简单近似(如对角近似或块对角近似),然后求逆得到预条件矩阵。不精确Newton法在每步迭代中通过采用PCG法近似求解Newton方程来获取本次迭代的更新方向。如果没有好的预条件矩阵,每步迭代中的PCG 求解过程收敛很慢,导致不精确Newton法的整体计算效率偏低[6]。拟Newton法是求解无约束优化问题的所有利用一阶导数信息的方法中最有效的一类方法[14],其中的L-BFGS法在FWI中得到了广泛应用[15-17]。
L-BFGS法不需要显式形成Hessian及其逆矩阵,在非线性优化方面表现出比CG法收敛快且稳健的优势[18]。该方法在每步迭代中都需要提供Hessian逆矩阵的一个初始近似矩阵。这个矩阵可以随迭代的进行而更新,也可以固定不变。初始矩阵的选取和更新方式对L-BFGS法的收敛性能有重要影响。但初始矩阵的选取并没有统一标准,需要根据具体优化问题而定[6]。如前文所述,PCG法采用的预条件矩阵即是对Hessian逆矩阵的近似。因而,选择初始矩阵时可以借鉴预条件矩阵的作法。此外,L-BFGS法需要存储一定数目的梯度残差和模型残差向量对,存储数目的多少也会对其收敛性能产生影响。
针对上述问题,我们分析了几种时间域可行的预条件矩阵的原理,对采用它们作为初始矩阵的L-BFGS法的反演性能进行了对比分析,并与相应的PCG法比较。此外,还分析了存储向量对的数目对L-BFGS法的影响。最后通过时间域的Marmousi模型FWI反演试验,来说明不同的初始矩阵选择以及更新方式对L-BFGS法收敛性能的影响。
1 时间域全波形反演理论简介
时间域波动方程的离散形式为
(1)
式中:u,S分别为波场和震源;m为模型参数,维数M;A(m)为正演矩阵。可以看出,A-1的每一列都对应于特定震源位置和特定激发时刻的Green函数。
设最小二乘目标函数为
(2)
式中:ns为炮数;ds是单炮观测记录;Rs为提取记录的算子。Newton法的更新方向满足
(3)

(4)

下面采用虚震源给出Jacobi矩阵的构造原理。分别在(1)式两边对m求导可得
(5)
定义F为虚震源,它的每一列代表该位置处模型参数的虚震源。虚震源中除了包含波场的作用外,还涉及到传播算子对模型参数的影响∂A/∂m,描述了数据对模型参数的随方位角变化的敏感性[19]。以F的每列为震源分别做正演模拟可以得到偏导波场,进而构造出Jacobi矩阵。因而,Gauss-Newton的近似Hessian矩阵可以写为
(6)

2 L-BFGS方法原理和初始矩阵的几种选择方法
L-BFGS法利用目标函数的一阶导数信息递归地计算近似Hessian逆矩阵与梯度的乘积,来得到迭代更新方向,克服了显式求取Hessian矩阵及其逆的困难,在FWI中应用广泛。
2.1 L-BFGS优化方法原理
每步迭代中近似Hessian逆矩阵与梯度向量乘积的具体计算公式为




(7)


(8)
这种初始矩阵在每次迭代中都可以更新[6]。以上2种方式并没有具体结合FWI中Hessian矩阵的特点。下面我们讨论几种针对时间域FWI的初始矩阵的选择方式。
2.2 L-BFGS法中初始矩阵的几种选择方式
预条件矩阵通常是由对Hessian矩阵做简单的近似,如对角近似或块对角近似,再求逆后得到。因而,初始矩阵的选取可以借鉴预条件矩阵的做法。在频率域也可以对Hessian矩阵做块对角近似[21],但在时间域计算块对角Hessian矩阵的运算量很大,所以一般并不可行。下面分析几种在时间域可行的对角预条件矩阵方式。
2.2.1 Pseudo Hessian(PH方式)
Shin等人[9]定义FTF为Pseudo Hessian,并用对角矩阵diag(FTF)来近似Hessian矩阵。从虚震源F的定义可知,这种方式只考虑了震源波场的作用和传播算子对模型参数的影响。它用单位矩阵替代(6)式的矩阵B,忽略了所有检波点处的Green函数对目标函数的影响。
2.2.2 New Pseudo Hessian(newPH方式)
这种方式是对上一种方式的改进,由Choi等人在频率域提出[10]。代替矩阵B的仍是对角矩阵,对角元素的值则是所有震源位置的Green函数在该空间点处的波场的振幅之和。如果观测系统中炮点和检波点有重合的位置,则这种方式能考虑重合部分的检波点处的Green函数的作用。在时间域可以采用类似的做法,用所有震源波场在地下同一点的振幅之和,作为代替矩阵B的对角矩阵在该位置的对角元素。
2.2.3 采用震源正传波场和记录残差反传波场的能量矩阵(RcdIW方式)
该方式采用震源正传波场与以模拟和观测记录的残差作为震源的反传波场的能量分布来构造梯度的预条件矩阵,目的是消除正、反传播过程中的几何扩散效应[11]。记u(x;xs)为xs处的震源的正传波场,λ(x;xr)为记录残差反传的波场,那么,正传波场的能量矩阵为
(9)
反传波场的能量矩阵为
(10)
对梯度进行预条件:
(11)
严格地讲,这种方式并不是对Hessian逆矩阵的近似,而是从波场能量分布的角度来对梯度进行校正。它考虑了记录残差反传波场的作用,但也携带了散射点的信息。采用它来预条件梯度会破坏模型扰动的聚焦。另外,该方式没有考虑传播算子对模型参数的影响。
2.2.4 采用震源正传波场和模拟记录反传波场的能量矩阵(ResIW方式)
该方法是对上一种方式的改进[12],不同之处在于采用的是模拟记录反传波场的能量分布,不会对模型扰动的聚焦造成破坏。但该方式同样没有考虑传播算子对模型参数的影响。它需要增加一次波场模拟来计算模拟记录的反传波场v(x;xr)。正传波场的能量矩阵仍采用(9)式。反传波场的能量矩阵以及预条件后的梯度分别为
2.2.5 用Hessian-vector 乘积构造对角矩阵
Korta等[13]在双参数FWI中采用这种方式构造块状对角的Hessian近似。在单参数FWI中,可以使用有限差分法[6]、二阶伴随状态法[22]或基于Born核函数的矩阵分解方法计算出Hessian-vector乘积Hv,其中v=(1,1,…,1,1)T。以该乘积为对角元素构造一个对角矩阵。此时,每个对角元素均为Hessian矩阵该行所有元素的叠加。如
果Hessian矩阵是严格对角占优的话,即对角线元素的绝对值大于同一行所有其它元素的绝对值之和,经过按行叠加得到的元素会偏离Hessian矩阵的主对角元素的精确值。如果不是严格对角占优,计算出的乘积很有可能是零或负值。即使取绝对值的话,数值试验表明其反演过程容易出现不稳定的现象。所以,在单参数FWI中,这种方式并不是合适的预条件矩阵。
3 数值反演试验
我们通过Marmousi模型合成数据的FWI反演数值试验,对比采用上述前4种方式作为初始矩阵的L-BFGS法的反演性能,同时与对应的预条件共轭梯度法进行比较。
从原始Marmousi模型中抽取了5940m×2980m的模型,实际模型(局部)和初始模型如图1 所示。网格剖分为298×150,网格间距20m。共使用56炮,间距为100m,检波器298个,间距为20m。时间采样间隔2ms,记录长度3s。震源采用主频7Hz的Ricker子波。采用空间4阶、时间2阶有限差分法求解常密度声波方程,四周均为PML吸收边界[23]。

图1 实际Marmousi模型(a)和初始模型(b)
3.1 残差向量对的数目对L-BFGS性能的影响
L-BFGS法构造近似Hessian逆矩阵时,需要存储r对梯度残差和模型残差。r越大,构造近似Hessian矩阵用到的信息越丰富,但所需内存也随之增大。假设模型向量的长度为M,则存储这些残差向量需要2M×r个浮点类型(float类型)的内存。首先,我们测试了L-BFGS法中需要存储的向量对的数目r对其性能的影响。
分别取r为 4,8,12,16和20,初始矩阵采用公式(8)的方式,对应的目标函数收敛曲线如图2。全波形反演的主要计算消耗为正演模拟,所以用目标函数随正演次数的变化来描述优化方法的收敛速度。可以看出,随着r的增大,L-BFGS法的收敛速度也加快。r=4时收敛最慢,r为8~20时收敛速度逐渐加快,但提升并不明显。当r=20时收敛最快,但存储残差向量的内存是r=8时的2.5倍。图3分别给出了r=8时的第324代(972次正演)和r=20时的第291代(873次正演)反演结果。此时,二者的目标函数均下降到1.01×10-3附近。图4分别对比了图3中反演结果在地表3km和5km处的纵向速度曲线。从图3 和图4可以看出,2个反演结果非常接近。因而,综合考虑收敛速度和内存消耗,参数r的取值无需过大。在此选取r=8。

图2 存储残差向量对的数目r对L-BFGS法目标函数收敛的影响

图3 存储不同向量对数目r的L-BFGS法的反演结果a r=8,第324代; b r=20,第291代

图4 对应图3中反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比
3.2 不同初始矩阵情况下的L-BFGS法的反演性能对比
我们分别选择前4种方式作为L-BFGS法的初始矩阵,即依次为PH,newPH,RcdIW和ResIW。初始矩阵在迭代过程中可以固定不变,也可以每次迭代都更新(Up1)。另外,一并测试单位矩阵(Identity)和公式(8)对应的矩阵(Nocedal)的情况。图5给出了不同初始矩阵、不同更新方式情况下的L-BFGS法的目标函数收敛曲线。
从图5可以看出,不同初始矩阵、不同更新方式的L-BFGS法的反演性能存在较大差异。按收敛速度快慢大致可以分为3类。
第一类收敛最快,包含以下5种方式。初始矩阵选取PH和newPH且固定不变时(蓝色和粉色虚线)收敛最快,二者非常接近。选RcdIW且固定不变时(绿色虚线)和选PH每次迭代都更新时(蓝色点划线)也比较接近,相比于前两种方式则稍微慢一些。选newPH且每代都更新时(粉色点划线)在开始阶段较慢,之后收敛加快。
选RcdIW且每代都更新时(绿色点划线)与选ResIW固定不变时(黑色虚线)收敛速度比较接近,属于第二类收敛较快的方式。
选ResIW且每代都更新(黑色点划线),Nocedal方式(红色实线)和Identity(青色实线)属于收敛比较慢的第三类。其中,单位矩阵并未提供有关Hessian的信息,收敛最慢。
综合以上对比结果可知,PH和newPH作初始矩阵且固定不变时,都可以快速收敛。RcdIW方式稍慢于前两者,可能与其未考虑正演算子对模型参数的影响有关。因存在不利于模型扰动聚焦的因素,ResIW在4种方式中收敛最慢。另外一个结论是,每种方式固定不变时(虚线)比每次迭代都更新(点划线)的收敛要快。这说明每次迭代更新初始矩阵所增加的计算消耗并未能带来目标函数的快速下降。
下面对比反演所得的速度模型。表1列出了
目标函数(归一化后)下降到1.01×10-3左右时,图5中各种方式的L-BFGS法所需要的迭代次数和正演次数的对比,其中单位矩阵(Identity)方式收敛最慢,只下降到1.202×10-3。图6是PH方式第88代和RcdIW方式第97代的反演结果,对应的目标函数值分别为1.016×10-3和1.011×10-3,正演次数则为264次和292次。图7给出了这两个模型在地表3km和5km处的纵向速度曲线的对比。可以看出,两种方式的反演结果非常接近,与真实模型也比较吻合。右下方包含高速体的区域则都存在偏差,对真实Hessian矩阵逼近的程度不够可能是原因之一。图7中还给出了PH方式第34代(102次正演)反演的速度曲线(粉色虚线),对应的目标函数值为1.03×10-3。此时的反演模型与真实模型有一定偏差,说明仍需迭代更新。从这些对比可以看出,当目标函数下降到基本相同的水平时,PH和RcdIW方式的反演结果也非常接近。而且,PH方式充当初始矩阵时在计算效率上占有少量优势。

图5 不同初始矩阵和不同更新方式的L-BFGS法的目标函数收敛曲线

NocedalPHnewPHRcdIWResIW目标函数值1.017×10-31.016×10-31.039×10-31.011×10-31.018×10-3正演次数966264250292507迭代次数322888397169IdentityPH-Up1newPH-Up1RcdIW-Up1ResIW-Up1目标函数值1.202×10-31.015×10-31.007×10-31.019×10-31.011×10-3正演次数999336336464849迭代次数33311284116283

图6 PH方式第88代(a)和RcdIW方式第97代(b)反演的速度模型
图8对比了PH方式第88代和newPH方式第83代反演结果的速度曲线。此时它们分别运行了264次和250次正演,效率相当,反演结果也非常相似。图9是PH方式第88代和ResIW方式第169代反演结果的速度曲线对比,可以看出反演结果比较接近。但所需正演次数分别为264次和507次。所以ResIW方式的计算效率偏低。
下面分析初始矩阵每次迭代都更新时的反演结果。图10是PH-Up1第112代(336,表示正演次数,下同)和PH第88代(264)反演结果的速度曲线对比。图11是RcdIW-Up1第116代(464)和RcdIW 第97代(292)的对比。可以看出,对于每种方式来说,当目标函数下降到基本相同的水平时,初始矩阵固定和每次迭代都更新这两种做法的反演结果很接近。但初始矩阵固定时计算效率更高。对于newPH和ResIW两种方式,结论相同。
综上可知,初始矩阵不变时,PH和newPH方式收敛最快,计算效率和反演结果均相当;RcdIW方式效率稍慢一些,ResIW方式则收敛较慢。以上4种方式作初始矩阵且每次迭代都更新时,L-BFGS方法的收敛速度要慢于初始矩阵固定不变的情况。因而,选好初始矩阵后,固定不变即可。初始矩阵选Nocedal方式和单位矩阵时收敛很慢。
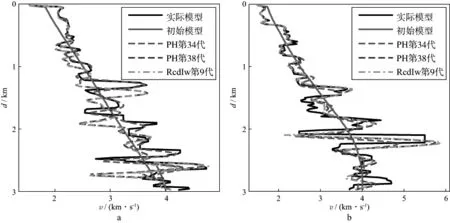
图7 对应图6中反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比

图8 PH方式和newPH方式反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比
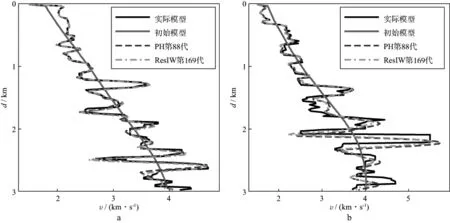
图9 PH方式和ResIW方式反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比

图10 PH-Up1方式和PH方式反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比

图11 RcdIW-Up1方式和RcdIW方式反演结果在地表3km(a)和5km(b)处的纵向速度曲线对比
此外,L-BFGS法构造近似Hessian逆矩阵时使用的是梯度残差向量。分别尝试采用PH,newPH,RcdIW和ResIW 4种方式预条件后的梯度残差向量来构造近似Hessian逆矩阵。如此进行的L-BFGS法FWI试验的收敛速度慢于上述作为初始矩阵的情况,而且容易导致反演不稳定。所以,不推荐对L-BFGS法中的梯度进行额外的预条件。
3.3 不同预条件CG法的反演性能对比
分别采用上述4种方式的预条件共轭梯度(CG)法进行同样的全波形反演试验。图12给出了4种预条件CG法与之前不同初始矩阵(固定)L-BFGS法的目标函数收敛曲线的对比。可以看出,在优化过程前期4种预条件CG法能达到和L-BFGS法比较接近的收敛速度,但都逐渐变慢。其中,ResIW预条件CG法收敛最慢。其它3种预条件CG法也都慢于初始矩阵固定的PH,newPH和RcdIW的L-BFGS法,但优于初始矩阵为单位矩阵和Nocedal的方式。所以,在全波形反演中选取适当的初始矩阵,可以使L-BFGS法的性能优于预条件CG法。这与Brossier等在频率域使用PH方式进行FWI的结论一致[16]。
表2列出了不做预条件的CG法和上述4种预条件CG法的反演过程中的一组数据对比,主要包括目标函数值、所需迭代次数以及正演次数。图13a 给出了PH方式的预条件CG法第258代反演的速度模型,此时正演次数为774次,目标函数值约为1.012×10-3。图13b则给出了RcdIW方式预条件CG法第203次迭代的结果,目标函数下降为1.014×10-3,正演次数为812次。
为了与采用对应方式作初始矩阵的L-BFGS法比较(图6),我们抽取了相应的速度曲线。图14 显示了PH方式的预条件CG法和作为L-BFGS法初始矩阵时反演结果的速度对比曲线。图15则是RcdIW方式的对比。可以看出,图6与图13对应的反演速度模型是非常接近的。从计算消耗上来说,初始矩阵为PH和RcdIW的L-BFGS法分别进行了264次和292次正演。可见其计算效率高于相应的预条件CG法。对于newPH方式也可以得到同样的结论,这里不再给出具体的图像和曲线。不做预条件的CG法和ResIW方式的预条件CG法的目标函数分别下降到1.604×10-3和1.948×10-3时,已经消耗掉约1000次正演,可见其效率偏低。
综合以上对比分析可以看出,尽管使用预条件矩阵可以提高CG法的效率,但仍不及采用同样方式作初始矩阵的L-BFGS法。

图12 不同预条件CG法与不同初始矩阵(固定)L-BFGS法的目标函数收敛曲线对比

CGPreCG-PHPreCG-newPHPreCG-RcdIWPreCG-ResIW目标函数值1.604×10-31.012×10-31.038×10-31.014×10-31.948×10-3正演次数999774698812999迭代次数333258174203333

图13 预条件CG法的反演结果a PH方式第258代; b RcdIW方式第203代

图14 PH方式预条件CG法和充当H0且固定不变时的L-BFGS法的反演结果在地表3km(a)和5km(b)处的vP曲线

图15 RcdIW方式预条件CG法和充当H0且固定不变的L-BFGS法的反演结果在地表3km(a)和5km(b)处的vP曲线
4 结束语
我们讨论了全波形反演中L-BFGS法的有效使用问题,主要分析了初始矩阵的选取方式和更新方式对L-BFGS法性能的影响。通过时间域Marmousi模型反演试验的比较,可以得出几点结论。
1) 初始矩阵固定不变时,只采用虚震源的PH方式和增加了震源波场振幅的newPH方式的L-BFGS方法收敛速度相当且最快。采用震源正传波场和模拟记录反传波场能量的RcdIW方式收敛稍慢。采用震源正传波场和记录残差反传波场能量的ResIW方式收敛明显慢于前3种方式,而使用Nocedal方式和单位矩阵的L-BFGS法收敛最慢。另外,在单参数FWI中,采用Hessian向量乘积构造对角矩阵的方式并不适合作为初始矩阵。
2) PH,newPH,RcdIW和ResIW4种方式作为初始矩阵且固定不变的L-BFGS法的收敛速度快于同种方式但初始矩阵每次迭代都更新的情形。
3) 与预条件CG法相比,采用同种方式作初始矩阵的L-BFGS方法收敛更快。
4) L-BFSG法的收敛速度会随存储的残差向量对的数目的增大而有所提升,但所需内存也会明显增多。因而综合计算效率和内存消耗的考虑,存储数目无需过大(如8左右)。
参 考 文 献
[1] Boonyasiriwat C,Schuster G T,Paul V,et al.Applications of multiscale waveform inversion to marine data using a flooding technique and dynamic early-arrival windows[J].Geophysics,2010,75(6):R129-R136
[2] 单蕊,卞爱飞,於文辉,等.利用叠前全波形反演进行储层预测[J].石油地球物理勘探,2011,46(4):629-633
Shan R,Bian A F,Yu W H,et al.Pre-stack full waveform inversion for reservoir prediction[J].Oil Geophysical Prospecting,2011,46(4):629-633
[3] Fichtner A,Kennett B L N,Igel H,et al.Full seismic waveform tomography for upper-mantle structure in the Australasian region using adjoint methods[J].Geophysical Journal International,2009,179(3):1703-1725
[4] Lailly P.The seismic inverse problem as a sequence of before stack migrations[C]∥Conference on inverse scattering:theory and application.NewYork:SIAM,1983:206-220
[5] Tarantola A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,49(8):1259-1266
[6] Nocedal J,Wright S J.Numerical optimization[M].2nd ed.New York:Springer,2006:101-184
[7] Pratt R G,Shin C,Hicks G J.Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J].Geophysical Journal International,1998,133(2):341-362
[8] Virieux J,Operto S.An overview of full-waveform inversion in exploration geophysics[J].Geophysics,2009,74(6):WCC1-WCC26
[9] Shin C,Jang S,Min D J.Improved amplitude preservation for prestack depth migration by inverse scattering theory[J].Geophysical Prospecting,2001,49(5):592-606
[10] Choi Y,Min D J,Shin C.Frequency-domain elastic full waveform inversion using the new pseudo-Hessian matrix:experience of elastic Marmousi-2 synthetic data[J].Bulletin of the Seismological Society of America,2008,98(5):2402-2415
[11] Zhang Z,Lin Y,Huang L.Full-waveform inversion in the time domain with an energy weighted gradient[J].Expanded Abstracts of 81stAnnual Internet SEG Mtg,2011,2772-2776
[12] Zhang Z,Lin Y,Huang L.A wave-energy-based precondition approach to full-waveform inversion in the time domain[J].Expanded Abstracts of 82ndAnnual Internet SEG Mtg,2012,1-5
[13] Korta N,Fichtner A,Sallaers V.Block-diagonal approximate hessian for Preconditioning in full waveform inversion[J].Expanded Abstracts of 75thEAGE Conference,2013,Tu-P04-16
[14] 袁亚湘.非线性优化计算方法[M].北京:科学出版社,2008:82-88
Yuan Y X.Computation Methods for Nonlinear Optimization[M].Beijing:Science Press,2008:82-88
[15] Guitton A,Symes W W.Robust inversion of seismic data using the Huber norm[J].Geophysics,2003,68(4):1310-1319
[16] Brossier R,Operto S,Virieux J.Seismic imaging of complex structures by 2D elastic frequency domain full-waveform inversion[J].Geophysics,2009,74(6):WCC105-WCC118
[17] Prieux V,Brossier R,Operto S,et al.Multi-parameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field.Part 1:imaging compressional wavespeed,density and attenuation[J].Geophysical Journal International,2013,194(3):1640-1664
[18] Kelley C T.Iterative methods for optimization[M].New York:SIAM,1999:71-83
[19] Gholami Y,Ribodetti A,Brossier R,et al.Sensitivity analysis of full waveform inversion in VTI media[J].Expanded Abstracts of 72ndEAGE Conference,2010,P371
[20] Plessix R E,Mulder W A.Frequency-domain finite-difference amplitude preserving migration[J].Geophysical Journal International,2004,157(3):975-987
[21] Hu W,Abubabak A,Habashy T M,et al.Preconditioned non-linear conjugate gradient method for frequency domain full waveform seismic inversion[J].Geophysical prospecting,2011,59(3):477-491
[22] Fichtner A,Trampert J.Hessian kernels of seismic data functionals based upon adjoint techniques[J].Geophysical Journal International,2009,185(2):775-798
[23] Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics,1994,114(2):185-200

