水力压裂微地震监测的震源机制反演方法应用研究

朱海波，杨心超，王 瑜，文 健

(1.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103;2.中国科学技术大学，安徽合肥230026)

微地震监测技术是水力压裂过程中了解压裂效果的一种非常重要的手段，通过对微地震事件的定位和能量大小估计裂缝发育的区域和几何形体。震源的矩张量反演是了解微地震事件相互作用与影响的重要研究工具，矩张量反演分析能够提供震源机制解，包括岩石破裂面的张裂和剪切滑动等属性，并获得破裂面的方向和倾角等参数，为水力压裂产生的复杂缝网的解释和进行有效压裂体积计算提供依据。

震源机制反演最初的研究工作集中在天然地震领域，Gilbert[1]首次引入矩张量的概念，并开辟了用矩张量表示震源的研究工作。在一阶近似的条件下，矩张量可以描述任意性质的震源。因此，许多学者开展了由地震波形资料反演地震矩张量的大量研究与应用试验。陈运泰等[2]给出了线弹性条件下任意倾角的走滑和倾滑断层面在地表引起的位移场的解析表达式;陈培善等[3]对断层的几何参数与矩震级之间的关系作了统计分析，获得了断层的长度、宽度、破裂面积、破裂长度与矩震级的关系;姚振兴等[4]给出了利用P波记录资料通过波形拟合和反演确定地震矩张量的方法;姚振兴等[5]还研究了时间域内有限地震断层破裂的正演和反演问题。

随着非常规油气藏的开发，特别是水力压裂技术的发展与应用，震源矩张量反演技术大量应用于微地震勘探中。Duncan[6]开展了水力压裂的地面微地震监测方法研究;Baig等[7]通过矩张量反演研究压裂裂缝的生长过程;Maxwell[8]对比研究了微地震变形与地质力学应变，反演了微地震震源特性以及对有效压裂体积的解释。

我们采用广义反透射系数方法[9]正演微地震的理论地震记录，通过求解观测记录和矩张量的线性方程组，反演出矩张量描述的震源机制解。通过西南地区某探井水力压裂微地震监测资料的试应用，获得了裂缝发育的方向和倾角等参数，为压裂裂缝的解释和压裂效果评价提供依据。

1 基本原理

广义反透射系数正演方法首先由Kennett等[10]于1979年提出，并给出了计算分层均匀介质所有响应的广义反射/透射系数矩阵方法。其计算过程是:首先求解波动方程，计算点源在自由表面上引起的频率-慢度域内的地面运动解，称为面谐矢量位移解;对面谐矢量解进行Fourier-Hankel积分反变换得到时间-空间域内的介质响应;通过与震源时间函数的褶积得到点源引起的地面运动解。在均匀、各向同性和完全弹性的水平层状介质(图1)中，某点P(r)的位移u(r,t)满足弹性波动方程:

(1)

式中:λ和μ为拉梅系数；f为体力。在柱坐标系(r,θ,z)下，位移u频率域的z分量表达式为

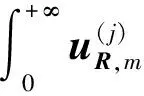
(2)

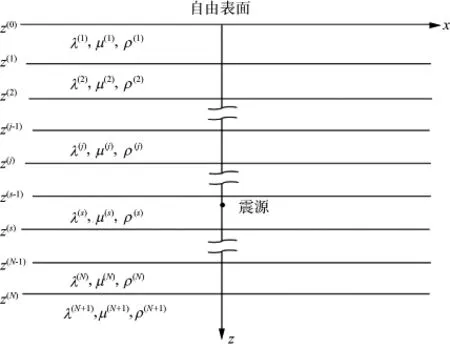
图1 水平层状介质模型

矩张量反演方法是采用观测到的地面位移推断震源属性，震源属性用矩张量描述。根据Aki等[11]的理论，假设存在一点震源，在接收点x处记录的位移场uk为

(3)

(k,i,j)∈(1,2,3)

式中:uk为检波点k方向的质点位移;(ξ,t′)为炮点坐标;Gki,j(x,t;ξ,t′)为包含炮点至检波点传播路线影响的格林函数，Gki,j=∂Gkj/∂ξj；Mij为地震矩张量。由于震源满足内源条件，地震矩张量为一个对称张量，有6个独立的分量，令m1=mxx，m2=mxy，m3=myy，m4=mxz，m5=myz，m6=mzz，又因为地震矩M=Mijf(t)，考虑到微地震的破裂时间很短，可近似认为f(t)=δ(t)，则(3)可改写为

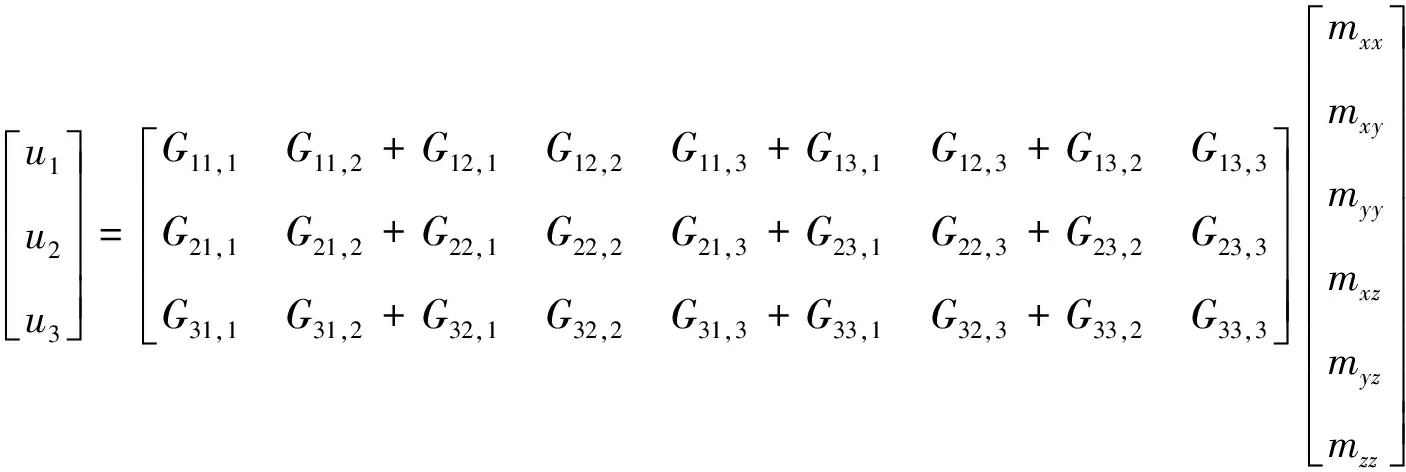
(4)

写成矢量形式:

(5)

公式(5)是一个线性方程组，利用奇异值分解对其求解，即可获得震源矩张量。

2 应用试例

2.1 理论模型测试

采用爆炸(ISO)震源的理论模型数据进行本文所论方法的有效性测试。其中，矩张量M=(1,0,0),(0，1，0),(0，0，1)，采用均匀介质模型，震源点和检波点位置及模型的观测方式如图2a 所示。井中震源深度为1200m;3个不同方向的检波点接收，检波点与震源在地面投影点的横向距离均为500m。图2b为广义反透射系数方法正演计算的P波垂向上的分量。通过矩张量反演获得了准确的矩张量M，结果如表1所示。图3为3个检波点的反演记录(蓝色线)和实际模型记录(紫色线)的对比结果，两者吻合较好，证明了本方法的有效性。

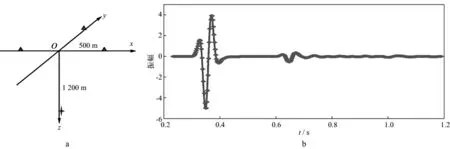
图2 模型数据观测系统(a)和广义反透射系数方法正演计算的理论震源记录(b)

MxxMyyMzzMxyMxzMyz理论值1.0000001.0000001.000000000反演值0.9999991.0000001.000000000

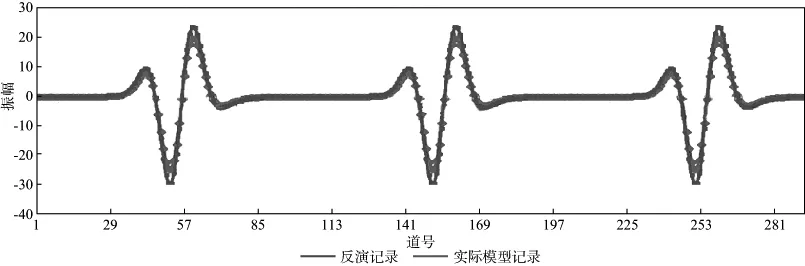
图3 模型数据反演记录与实际模型记录的对比

2.2 实际数据试应用

选取我国西南地区某压裂井的微地震数据进行本文所论方法的试应用。该压裂井目标层段埋深大于3000m，上部为粉砂岩夹泥页岩，下部为泥页岩夹砂岩;目标井段裂缝发育。

压裂监测方式采用地面微地震监测，观测系统呈扇形分布(图4)，其中最小偏移距为300m，最大偏移距为3300m，道间距为25m，1210个检波点接收，共10条线。压裂过程中共接收到了800多个微地震信号，通过对微地震信号事件的预处理(校正、滤波和去噪等)，获得的有效微地震事件记录如图5所示。该事件的定位结果见图4中红色三角标示。

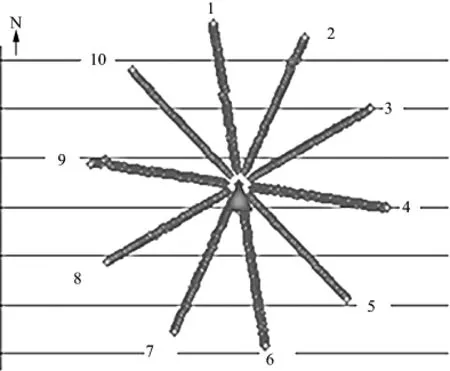
图4 地面微地震监测的观测系统示意图解

从岩石断裂力学可知，压裂过程中产生的破裂主要有张开型、剪切型和滑动型3种类型。水力压裂过程中监测到的破裂主要以剪切裂缝为主，剪切裂缝的属性参数(如方位角、倾角和滑动角)确定了地面观测记录的极性变化[6]。因此，有效识别微地震记录的极性变化对于矩张量反演结果的准确与稳定有着非常重要的作用。图5中红线标记部分表示信号的极性发生反转(图中横坐标上红色小三角表示线号)，可以清楚地看到，观测系统中的第1,8,9,10号接收线存在着明显的P波极性反转。

图5 西南地区某压裂井有效微地震事件记录

反演过程中首先需要计算震源的格林函数(见公式(4))，其速度模型采用图6所示的测井速度曲线。为了保证反演的可靠性，首先需要用已定位的震源位置进行正演，并适当调整速度模型，以使正演结果与实际的微地震信号有较好的匹配。

图6 测井P波速度曲线

在反演过程中，由于实际观测的检波点数量较多，在解线性方程组(公式(5))时需要消耗大量的内存空间，为了提高计算效率，只选取了部分检波点数据进行反演。检波点选取的原则是尽可能反映极性和振幅的变化，因此，在信号极性变化的线选用相对较多的检波点，在信号极性没有变化的线则选用相对较少的检波点，这里共选用了213个检波点数据，如图7所示。

图7 反演选取的检波点

为了降低噪声的影响，保证反演的稳定性，对于选取的检波点记录进行了相邻道叠加加强、道间时差校正、道间频率匹配和滤波，通过上述处理，使反演输入的波形较稳定，且信噪比较高。图8为处理后提取的部分观测记录。通过反演获得震源机制解(表2)，由于微地震信号振幅的量纲未知，因此，其解表示力矩在不同方向的相对关系，无法确定解的绝对量纲。其对应的两组节面如图9所示(向上为正北轴)。根据对多个事件的定位分析和相关的地质认识，解释确定出方位角25.2°，倾角72.1°和滑动角-118.4°为裂缝面。

再通过正演来验证反演结果的可靠性。对图9 解释的裂缝参数进行正演，模拟出了所选取的213个检波点的理论记录(图10a)，与实际观测数据(图10b)进行对比(未经过动校正处理)。从图10 中可以看出,反演结果正演模拟记录的极性与实际观测记录相符合，除了130道至150道附近的检波点记录相对能量较弱外，其余检波点记录之间保持了很好的振幅相对关系，由此证明反演结果具有较高的可靠性。

图8 提取的部分观测记录(反动校正后)

MxxMyyMzz0.322 293-0.120 332-0.750 825MxyMxzMyz-0.439 504-0.114 2880.789 702

图9 反演获得的震源机制解(沙滩球)

图10 反演结果的正演模拟记录(a)和实际观测记录(b)

3 结束语

采用广义反透射系数方法正演计算理论地震记录，用矩张量描述震源属性，通过奇异值分解反演出震源机制解，并应用于实际水力压裂监测中所记录的微地震事件解释，获得了微地震事件的方位角、地层倾角和滑动角等地质参数，结合实际地质情况和微地震事件的定位，为压裂裂缝的解释和压裂效果评价提供依据。

参 考 文 献

[1] Gilbert F.Excitation of the normal modes of the earth by earthquake sources[J].Geophysical Journal of the Royal Astronomical Society,1971,22(2):223-226

[2] 陈运泰，林邦慧，林中洋，等.根据地面形变的观测研究1966年邢台地震的震源过程[J].地球物理学报，1975,18(3):164-181

Chen Y T,Lin B H,Lin Z Y,et al.The focal mechanism of the 1966 Xingtai Earthquake as inferred from the ground deformation observations[J].Chinese Journal of Geophysics，1975,18(3):164-181

[3] 陈培善，白彤霞.震源参数之间的定量关系[J].地震学报,1991,13(4):401-410

Chen P S,Bai T X.The quantitative relations between the source parameters[J].Chinese Journal of Geophysics,1991，13(4):401-410

[4] 姚振兴，郑天愉.用P波波形资料反演中强地震地震矩张量的方法[J].地球物理学报，1994,37(1):36-45

Yao Z X,Zhen T Y.Moment tensor inversion method for determining the earthquake process by the use of P-wave form data[J].Chinese Journal of Geophysics,1994,37(1):36-45

[5] 姚振兴，纪晨.时间域内有限地震断层的反演问题[J].地球物理学报，1997，40(5):691-700

Yao Z X,Ji C.The inverse problem of finite fault study in time domain[J].Chinese Journal of Geophysics,1997,40(5):691-700

[6] Duncan M.Is there a future for passive seismic[J].First Break,2005,23(6):111-115

[7] Baig A,Urbancic T.Microseismic moment tensors:a path to understanding fracture growth[J].The Leading Edge,2010,29(3):320-325

[8] Maxwell S C.What does micro-seismic tell us about hydraulic fracture deformation[EB/OL].[2013-11-20].http:∥wenku.baidu.com/link?url=KmGJ9n

PYg2TO_AkclD2KL9YxaBpHx3QQ5R74FSCtpEV

YciladI9t1bFCLAuPhmno368jqiVkaYRE4pYHrDR-8At8snxpt0wLLgLL4umcGyK

[9] Chen X F.Seismogram synthesis in multi-layered half space,part I:theoretical formulation[J].Earthquake Research in China,1999,13(2):149-175

[10] Kennett B L N,Kerry N J.Seismic waves in a stratified half space[J].Geophysical Journal International,1979,57(3):557-583

[11] Aki K,Richards P G.Quantitative seismology:theory and methods[M].2nd ed.USA:University Science Books,2002:1-704

[12] Sherilyn W,Jo E K.Moving outside of the borehole:characterizing natural fractures through micro-seismic monitoring[J].First Break,2010,28(1):89-95

[13] Duncan P M,Eisner L.Reservoir characterization using surface micro-seismic monitoring[J].Geophysics,2010,75(5):A139-A146

[14] Gajewski D,Tessmer E.Reverse modeling for seismic event characterization[J].Geophysical Journal International,2005,163(1):276-284

[15] Anikiev D,Stanek F,Valenta J,et al.Imaging micro-seismic events by diffraction stacking with moment tensor inversion[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013,2013-2018