TTI介质弹性波随机边界逆时偏移的实现
秦海旭,吴国忱
(中国石油大学(华东)地球科学与技术学院,山东青岛266580)
常规地震资料偏移方法主要有单程波动方程偏移和克希霍夫偏移,这两种方法都无法对复杂介质精确成像。双程波动方程逆时偏移是一种基于波动理论的深度域偏移方法,地震波的近似较少,不受地层倾角的影响,能够处理纵向、横向变速问题,是目前最精确的偏移方法。
逆时偏移思想由Hemon[1]于1978年提出。Whitmore[2]1983年在第53届SEG年会上首次给出了逆时偏移方法。Baysal等[3],McMechan[4],Loewenthal等[5]先后将逆时偏移方法用于叠后地震资料偏移处理。随着计算机技术的发展和方法研究与应用的逐步深化,逆时偏移已经从叠后发展到叠前,从二维发展到三维[6],从声波方程发展到弹性波方程[7],从各向同性介质发展到各向异性介质[8-11],从单分量资料发展到多分量资料[12]。根据所采用的模拟方法不同,逆时偏移可以分为有限差分逆时偏移[13]、伪谱法逆时偏移[14]、有限元逆时偏移[15]、混合法逆时偏移[16]。逆时偏移的成像条件包括激发成像条件、互相关成像条件、归一化互相关成像条件以及振幅比成像条件[17]等。
传统的逆时偏移存在计算量大、存储量大以及低频噪声能量强等缺陷。针对计算量大、运算速度慢的问题,刘红伟等[18]采用GPU(加速30倍)实现了高阶有限差分逆时偏移。而压制低频噪声的途径主要有3类,一是修改波动方程[19-20],二是修改成像条件[21],三是拉普拉斯成像后滤波[22]。
目前,声学介质和VTI介质的逆时偏移技术已经成熟,而TTI介质特别是TTI介质弹性波逆时偏移发展较为缓慢。这是因为相对于各向同性介质和VTI介质,TTI介质波动方程更复杂,稳定性要求更高,同样的空间网格需要更小的时间采样间隔,从而需要更大的存储空间。同时,由于对称轴倾角的存在,TTI介质有限差分外推算子更易产生频散,需要深入研究消除频散的有效方法。随着计算机技术的发展,尤其是油气勘探生产实际需求的增长,对TTI介质弹性波逆时偏移方法的实用化研究已经非常必要。
我们引入用计算换存储的思路,采用随机边界条件有效减少存储空间,给出了便于实际应用的TTI介质弹性波随机边界逆时偏移方法实现流程,通过模型试算证明了该方法流程的正确性与有效性。
1 TTI介质弹性波差分方程的建立
二维TTI介质弹性波方程如下:
(1)
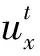

(4)

(5)
式中:am为2阶偏导数差分系数;ωm为混合偏导数的差分系数。公式(2)为震源x分量正向延拓的高阶差分格式;公式(3)为地震记录x分量逆向延拓的高阶差分格式;公式(4)为震源z分量正向延拓的高阶差分格式;公式(5)为地震记录z分量逆向延拓的高阶差分格式。本文采用时间2阶、空间10阶的差分格式,所以M=5,其中差分系数为a0=-5.8500,a1=3.3330,a2=-0.4760,a3=0.0790,a4=-0.0010,a5=0.0006,ω1=0.8330,ω2=-0.2380,ω3=0.0595,ω4=-0.0100,ω5=0.0070。由于TTI介质的稳定性要求相对于各向同性介质与VTI介质要求更高,并且由于对称轴倾角的存在,TTI介质有限差分外推算子更易产生频散,因此,在逆时偏移与正演过程中采用完全匹配层(PML)吸收边界压制边界反射,采用高阶有限差分与通量传输校正(FCT)方法压制网格频散,利用互相关成像条件,通过公式(2)—公式(5)递推的方法建立常规的TTI介质弹性波有限差分逆时偏移流程,如图1所示。
采用PML吸收边界的常规TTI介质弹性波有限差分逆时偏移流程包括以下几步:①计算震源正向传播的地震波场;②计算地震记录反向传播的地震波场;③将正向传播的地震波场和反向传播的地震波场利用互相关成像条件完成单炮偏移;④将所有单炮的偏移结果叠加完成多炮偏移。该逆时偏移流程的实现过程中需要存储正向传播的地震波场,将占用大量的存储空间,这里以一个简单的双层TTI介质模型予以说明。
如图2所示,模型大小为2000m×2000m,横向和纵向采样间隔均为10m,时间采样间隔为1ms,时间长度为1.5s,震源为主频20Hz的雷克子波。图中vP,vS,ρ分别为纵波速度、横波速度与密度;ε,γ为各向异性参数;φ为对称轴倾角。针对此模型的单炮偏移过程中,地震记录逆向延拓所用时间为255s,震源正向延拓所用时间为255s,成像条件所用时间为5s,总共所需要的计算时间为515s。逆时偏移过程中需要存储震源正向传播的波场,大约需要的存储空间为457M。实际处理中假设数据体大小是10000m×10000m,10000个时间采样点,那么其单炮偏移所占用的存储空间就高达80G,可见常规的TTI介质弹性波有限差分逆时偏移流程不利于实际应用。

图1 常规的TTI介质弹性波有限差分逆时偏移流程

图2 双层TTI介质模型
2 TTI介质随机边界逆时偏移流程
由以上分析可见,常规TTI介质弹性波逆时偏移因占用大量的存储空间而不便于实际应用。为了解决这个问题,Clapp[23]等提出了随机边界条件,使波场外推变成一个可逆的过程,用计算换存储,节约了存储空间。其方法是:首先将震源正向传播的地震波场递推到最大时间,然后与地震记录同时逆时外推,每递推一个时间步长做一次互相关成像,最后将所有时间的成像结果进行叠加,从而有效地解决了逆时偏移中的边界及存储问题。本文采用随机边界条件,同样通过高阶有限差分算子和FCT方法解决TTI介质频散严重的问题,并通过缩小时间采样间隔来满足TTI介质逆时偏移中对稳定性的高要求,由此形成的TTI介质弹性波随机边界有限差分逆时偏移流程如图3所示。与传统的PML吸收边界逆时偏移算法相比,随机边界逆时偏移算法增加了一次震源波场的延拓过程,却减少了震源波场的大批量存储与读取,有利于TTI介质弹性波逆时偏移的实用化。
为了说明随机边界波场外推的可逆过程,设计一个2000m×2000m的匀速TTI介质模型,其中vP=3500m/s,vS=2000m/s,ρ=2400kg/m3,ε=0.16,δ=0.05,γ=0.15,φ=60°。图4a为未加随机边界的匀速模型;图4b为加上随机边界的匀速模型。取纵向、横向采样间隔均为10m,采用主频为20Hz的雷克子波进行模拟试算,时间采样间隔为1ms,时间长度为0.7s,结果如图4c到图4f 所示。其中图4c和图4d分别为正向传播时间t=0.2s时x分量和z分量的地震波场;图4e和图4f分别为反向逆推到t=0.2s时x分量和z分量的地震波场。由图4c至图4f可见,正向传播的地震波场和反向传播的地震波场(x分量和z分量)基本一致,虽然存在少量的噪声,但由于反射波相关性很差,因此不会对成像结果产生影响。

图3 TTI介质弹性波随机边界有限差分逆时偏移流程

图4 匀速TTI介质模型的随机边界逆时偏移a 未加随机边界的匀速模型; b 加上随机边界的匀速模型; c t=0.2时刻x分量地震波场; d t=0.2s时刻z分量地震波场; e 逆推到t=0.2时刻x分量地震波场; f 逆推到t=0.2时刻z分量地震波场
对于图2所示的双层TTI介质模型,随机边界逆时偏移不需要大量的存储空间,但是需要多进行一次随机边界正演模拟,随机边界单炮正演所用时间为150s,大约为常规有限差分逆时偏移所用时间的30%。对图2所示双层TTI介质模型分别采用图1和图3所示的逆时偏移流程进行单炮逆时偏移,最后将所有单炮偏移结果(40炮)进行叠加,结果如图5所示。其中图5a和图5b分别为常规逆时偏移的x分量和z分量结果;图5c和图5d分别为随机边界逆时偏移的x分量和z分量结果。逆时偏移横向、纵向采样间隔均为10m,时间采样间隔为1ms,时间长度为1.5s,震源为主频20Hz的雷克子波。由图5可见,随机边界逆时偏移结果虽然存在少量的噪声,但与常规逆时偏移结果的成像界面位置一致,证明了随机边界逆时偏移方法的正确性。

图5 双层TTI介质模型的常规逆时偏移和随机边界逆时偏移结果a 常规逆时偏移x分量结果; b 常规逆时偏移z分量结果; c 随机边界逆时偏移x分量结果; d 随机边界逆时偏移z分量结果
3 拉普拉斯滤波压制低频成像噪声
本文所述TTI介质弹性波逆时偏移方法采用的互相关成像条件,是由Claerbout[24]提出的反射地震成像原理演变而来的,成像点位于入射波初至和反射波产生时间相同的点上。逆时偏移中震源正向延拓的地震波场可以看作是上行波,地震记录逆时延拓的地震波场可以看作是下行波,但逆时偏移中地震波场并不能完全有效地分开,首波、潜水波、散射波等干扰波也满足互相关成像条件而产生虚假的成像点,造成低频干扰,其主要出现在浅层和强反射界面上(图5)。因此,逆时偏移中压制低频噪声是一项重要的处理内容。本文采用拉普拉斯滤波方法在成像后压制低频噪声,该方法具有简单、易于实现和不受模型限制等优点。图6为对图5 所示的逆时偏移结果进行拉普拉斯滤波后的结果,其中图6a和图6b分别为常规逆时偏移的x分量和z分量滤波结果,图6c和图6d分别为随机边界逆时偏移的x分量和z分量滤波结果。

图6 双层TTI介质模型常规逆时偏移和随机边界逆时偏移后的拉普拉斯滤波结果a 常规逆时偏移x分量; b 常规逆时偏移z分量; c 随机边界逆时偏移x分量; d 随机边界逆时偏移z分量
4 模型测试算例
4.1 多层模型算例
多层TTI介质模型如图7所示,模型大小为4000m×4000m,纵、横向采样间隔均为10m。模型参数见表1所示,其中vP,vS,ρ分别为纵波速度、横波速度与密度;ε,δ,γ为各向异性参数;φ为对称轴倾角。震源采用主频为25Hz的雷克子波,时间步长为1ms,时间长度为4s。采用时间2阶、空间10阶的有限差分格式进行逆时偏移,检波器布置于整个地表,道间距为10m,共400个检波点。分别采用图1和图3所示的逆时偏移流程进行多炮偏移并叠加,然后采用拉普拉斯滤波方法压制浅层低频噪声,结果如图8所示。
图8a和图8b分别为常规逆时偏移的x分量和z分量滤波结果;图8c和图8d分别为随机边界逆时偏移的x分量和z分量滤波结果。对比图8a
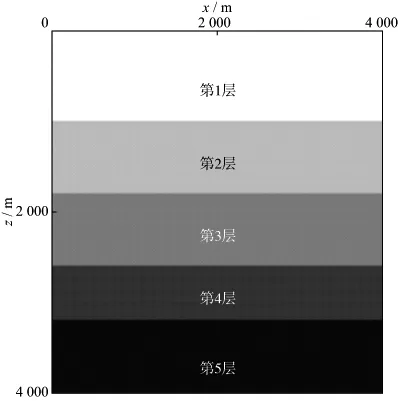
图7 多层TTI介质模型
与图8c,图8b与图8d,可见随机边界逆时偏移与常规有限差分逆时偏移的成像界面位置一致,即随机边界逆时偏移方法能对多层模型的每一层界面准确地成像,证明了本文方法的有效性。图8c和图8d的随机边界偏移结果中尚存在少量噪声,该噪声的有效消除将是我们下一步的研究重点。
对于多层TTI介质模型,采用图1所示流程的常规逆时偏移占用存储空间为95.3674G,所用计算时间为3.86h;而采用图3所示流程的随机边界逆时偏移占用存储空间为24.4M,所用计算时间为5.10h。可见随机边界逆时偏移相对于常规逆时偏移多用大约30%的计算耗时就能节约大约99.9%的存储空间,减少了大量的存储量,便于TTI介质弹性波逆时偏移方法的实际应用。

表1 多层TTI介质模型参数

图8 多层TTI介质模型的常规逆时偏移和随机边界逆时偏移加拉普拉斯滤波结果a 常规逆时偏移x分量结果; b 常规逆时偏移z分量结果; c 随机边界逆时偏移x分量结果; d 随机边界逆时偏移z分量结果
4.2 逆掩断层模型算例
逆掩断层TTI介质模型如图9所示,具体参数见表2(各参数含义同多层模型)。模型大小为4000m×4000m,纵、横向采样间隔均为10m。采用与多层模型模拟试算相同的观测方式和计算流程进行逆时偏移,图10a和图10b分别为常规逆时偏移的x分量和z分量滤波结果;图10c和图10d 分别为随机边界逆时偏移的x分量和z分量滤波结果。对比图10a与图10c,图10b与图10d,可见随机边界逆时偏移结果存在少量的噪声,但随机边界逆时偏移与常规有限差分逆时偏移的成像界面位置一致,且随机边界逆时偏移对于逆掩断层及其拐点均能精确地成像,进一步证明了该方法的正确性和有效性。

图9 逆掩断层TTI介质模型
对于逆掩断层TTI介质模型,采用如图1所示流程的常规逆时偏移占用存储空间为95.4628G,所用计算时间为3.93h;而采用如图3 所示流程的随机边界逆时偏移占用存储空间为97.6536M,所用计算时间为5.15h。与多层TTI介质模型逆时偏移的情况类似,逆掩断层TTI介质模型的随机边界逆时偏移相对于常规逆时偏移也只多用大约30%的计算耗时,就节约了99.9%左右的存储空间。可见随机边界逆时偏移大幅度减少了存储量,便于TTI介质弹性波逆时偏移方法的实际应用。

表2 逆掩断层TTI介质模型参数
5 结束语
本文研究表明,随机边界逆时偏移相对于常规有限差分逆时偏移需要多进行一次随机边界正演模拟,比常规逆时偏移大约多用30%的计算时间,但比常规逆时偏移节省了大量的存储空间,便于TTI介质弹性波逆时偏移方法的实际应用。多层模型和逆掩断层模型的随机边界逆时偏移与常规有限差分逆时偏移的成像位置一致,证明了TTI介质弹性波随机边界逆时偏移方法流程的正确性和有效性。然而,随机边界逆时偏移引入的噪声问题、正演模拟算法的数值稳定性问题和对称轴倾角引发的频散问题,仍是TTI介质弹性波逆时偏移方法实用化有待进一步研究的重点内容。
参 考 文 献
[1] Hemon C H.Equations d’onde et modeles[J].Geophysical Prospecting,1978,26(4):790-821
[2] Whitmore N D.Iterative depth migration by backward time propagation[J].Expanded Abstracts of 53rdAnnual Internat SEG Mtg,1983,382-386
[3] Baysal E,Kosloff D D,Sherwood J W.Reverse time migration[J].Geophysics,1983,48(11):1514-1542
[4] McMechan G A.Migration by extrapolation of time-dependent boundary values[J].Geophysical Prospecting,1983,31(3):413-420
[5] Loewenthal D,Mufti I R.Reversed time migration in spatial frequency domain[J].Geophysics,1983,48(5):627-635
[6] Chang W F,McMechan G A.3D acoustic pre-stack reverse time migration[J].Geophysical Prospecting,1990,38(7):737-756
[7] Chang W F,McMechan G A.3D elastic pre-stack reverse time depth migration[J].Geophysics,1994,59(4):597-609
[8] Zhang H Z,Zhang Y.Reversed time migration in 3D heterogeneous TTI media[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2196-2200
[9] Du X,Bancroft J C,Lines L R.Reversed time migration for titled TI media[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,1930-1935
[10] Huang T,Zhang Y,Zhang H Z,et al.Subsalt imaging using TTI reverse time migration[J].The Leading Eage,2009,28(4):448-452
[11] Zhang Y,Zhang H Z.A stable TTI reverse time migration and its implementation[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009,2794-1798
[12] 杜启振,秦童.横向各向同性介质弹性波多分量叠前逆时偏移[J].地球物理学报,2009,52(3):801-807
Du Q Z,Qin T.Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J].Chinese Journal of Geophysics,2009,52(3):801-807
[13] 陈可洋.基于高阶有限差分的波动方程叠前逆时偏移方法[J].石油物探,2009,48(5):475-498
Chen K Y.Wave equaction pre-stack reverse-time migration method based on high order finite-difference approach[J].Geophysical Prospecting for Petroleum,2009,48(5):475-498
[14] 王童奎,付兴深,朱德献,等.谱元法叠前逆时偏移研究[J].地球物理学进展,2008,23(3):681-655
Wang T K,Fu X S,Zhu D X.Spectral element method for prestack reverse-time migration[J].Progress in Geophysics,2008,23(3):681-655
[15] 张美根,王妙月.各向异性弹性波有限元叠前逆时偏移[J].地球物理学报,2001,44(5):711-719
Zhang M G,Wang M Y.Prestack finite element reverse-time migration for anisotropic elastic waves[J].Chinese Journal of Geophysics,2001,44(5):711-719
[16] 王山山,聂勋碧,邓玉琼.混合法双程无反射波动方程偏移[J].石油地球物理勘探,1993,28(5):537-542
Wang S S,Nie X B,Deng Y Q.Hybrid migration using two-way nonreflecting wave equation[J].Oil Geophysical Prospecting,1993,28(5):537-542
[17] Chattopadhyay S,McMechan G A.Imaging conditions for prestack reverse-time migration[J].Geophysics,2008,73(3):81-89
[18] 刘红伟,李博,刘红,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报2010,53(7):1725-1733
Liu H W,Li B,Liu H,et al.The algorithm of high order finite difference per-stack reverse time migration and GPU implementation[J].Chinese Journal of Geophysics,2010,53(7):1725-1733
[19] Baysal E,Kosloff D D,Sherwoods W C.A two way nonreflecting wave eqation[J].Geophysics,1984,49(2):132-141
[20] Loewenthal D,Stoffa P L,Farias E L.Suppressing the unwanted reflections of the full wave equation[J].Geophysics,1987,52(7):1007-1012
[21] Kaelin B,Guitton A.Imaging condition for reverse time migration[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2594-2598
[22] 刘红伟,刘红,邹振,等.地震叠前逆时偏移中的去噪与存储[J].地球物理学报,2010,53(9):2170-2180
Liu H W,Liu H,Zou Z,et al.The problems of denoise and storage in seismic reverse time migration[J].Chinese Journal of Geophysics,2010,53(9):2170-2180
[23] Clapp R G.Reverse time migration with random boundaries[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009,2809-2813
[24] Claerbout J F.Toward a unified theory of reflection mapping[J].Geophysics,1994,36(3):467-480

