考虑多种应力的组合截面填板承载力研究
杨隆宇
(中国电力工程顾问集团 华北电力设计院工程有限公司,北京100120)
0 引言
目前输电线路杆塔结构所用钢材屈服强度不断增加[1,2],组合截面大量使用[3~5],而连接角钢的填板受力情况非常复杂。
文献[6]中仅简要给出填板的构造要求,文献[7]中,根据材料力学的原理来设计填板所受剪力。左元龙等[8]结合构件试验,得到了填板剪力的计算公式。钟寅亥等[9]通过计算构件横向、纵向剪力对填板优化设计做了讨论。杨利容等[10]根据不同钢结构设计规范的方法,推导出填板和螺栓的设计公式。
现有研究所用填板简化模型与实际受力状态会有较大偏差。因此,根据双角钢十字截面构件的试验、有限元计算,考虑角钢和填板尺寸等多因素的影响,得到填板实际受力状态并据此给出建议的设计公式,为工程实践提供依据。
1 试验概况
试验选取特高压输电塔工程中常用的Q420 高强角钢(L160 ×12,L160 ×14,L160 ×16),构件中填板形式为一字连接[5],长细比范围为25~55;构件两端采用靴板连接。板件间所有连接均采用螺栓,螺栓孔径、间距等与实际一致。试件两端靴板连接至球形铰支座,试验在10 000 kN 压力机上进行,试验装置见图1。

图1 试验装置图
为确定构件极限承载力、考察加载过程中构件变形及应力- 应变变化关系,逐级加载稳定1 min后用动态应变仪记录相应荷载的应变。应变片每层布置8 片(每个角钢的每肢布置2 片),层间距随角钢长细比变化,布置见图2。试验角钢的材性试验构件和试验过程按规范[11]进行。

图2 角钢截面图
2 试验结果
试验结果按已有方法[3~5]用角钢材性试验结果及实测尺寸对构件屈服强度、截面积进行折减,换算成标准屈服强度和截面积。所得柱子曲线见图3。

图3 柱子曲线
图中曲线在λ=35(无量纲长细比λn=0.50)和λ=40(λn=0.57)之间,曲线出现了波动,并非按规范[6,7]柱子曲线形式均匀下降,这是因为试验构件按构造要求在λ=35 时构件采用了1 块填板,在λ=40 时构件采用了2 块填板,填板数量影响了构件的承载力。图4 为构件一个截面上记录的荷载-应变曲线,从图中可以看到在加载初期(弹性阶段),同一横截面上各点应变随着外荷载线性增加;当荷载继续增大、构件出现轻微弯曲变形时,截面进入弹塑性阶段,荷载-应变曲线开始呈现非线性特征;当荷载进一步加大,到达临界荷载时,构件发生明显的弯曲屈曲并伴随角钢的局部翘曲(图1),构件外凸侧纤维被拉伸、出现一定程度的卸荷,此时荷载-应变曲线向原点方向开展,而内凹侧纤维在外荷载和压缩变形共同作用下,应变迅速增大,荷载-应变曲线在失稳瞬间接近水平。

图4 荷载-应变曲线
3 有限元分析
为与双角钢构件的材性试验结果保持一致,设定有限元模型采用图5 所示本构关系。

图5 有限元模型本构关系
根据已有研究[4~6]和本次分析的具体情况,将构件简化为图6 所示等效模型,模型相关参数与构件试验条件相同。角钢模型采用二维单元,在厚度上分层易产生病态单元、降低计算精度;填板采用三维单元以体现填板对双角钢在空间上的分隔作用;模型两端连接高刚度端板作为加载板,与试验一致。综合考虑构件初始缺陷(包括初始偏心、初始弯曲、安装误差、残余应力等)对计算的影响[5]。
模型计算结果如图7 所示,从中可以看出,构件变形形态及应力分布与实际相符。

图6 模型单元划分图

图7 模型计算结果
有限元计算结果与试验结果的对比见表1,表中数据为各构件值(PEXP)与模型计算值(PFEA)的比值。从表中可看出,二者平均差值在5%以内,该结果显示有限元模型具有较好的精度,可作为进一步分析的基础。

表1 试验值与有限元值对比
4 填板参数化有限元分析
为研究填板的受力状态,把上述有限元模型中填板的网格加密,并优化填板和角钢的连接,以得到填板部分更精确的求解结果。模型边界条件等设置与试验条件相同。模型中填板间距按规范要求布置[6,7],选择规范中[12]肢宽70 mm-250 mm的等边角钢的所规格建立双角钢模型,模型fy=420 MPa。
求解后提取临界荷载对应数据,在填板中心建立图8 所示坐标系,提取填板模型在XOZ 截面上各单元应力并对相应坐标轴积分,得到横截面上轴向力Fx,Fy,Fz和弯矩Mx,Mz。

图8 模型坐标系
根据角钢屈曲变形的不同,填板受力可有多种可能,截面应力分布中两种有代表性的情况如图9 所示。图9(a)中轴向力几乎都朝坐标轴的一个方向,此时截面以法向力为主,弯矩较小;图9(b)是受弯构件横截面典型的应力分布图,此时截面法向力相对小,弯矩比图9(a)明显增大。其他更复杂的应力状态中截面法向力分布介于二者之间。

图9 填板横截面应力分布图
图10 中横坐标为双角钢构件截面面积,两纵轴分别是Mx和Mz。随着角钢截面规格(即构件承载力)的增大,填板横截面上两个方向弯矩都逐渐增大,Mx比Mz大一个数量级,表明角钢两端横截面的相对转动是引起填板截面上弯矩的主要原因。
图11 和图12 分别是填板横截面单元上3 个轴向力和3 个方向剪力的计算结果,横坐标为构件截面积。从两图中可知,3 个轴向力Fy>Fz>Fx,3 个剪力Qxy>Qyz>Qxz,这与双角钢构件实际屈曲变形结果是一致的,表明填板为使两角钢协同工作,在角钢屈曲和翘曲的作用下处于复杂应力状态。其中Fx与Qxz在所有角钢规格的构件中都相对较小,说明模型两端的铰支座没有迫使构件截面间发生相对转动,起到了球形铰支座的作用。
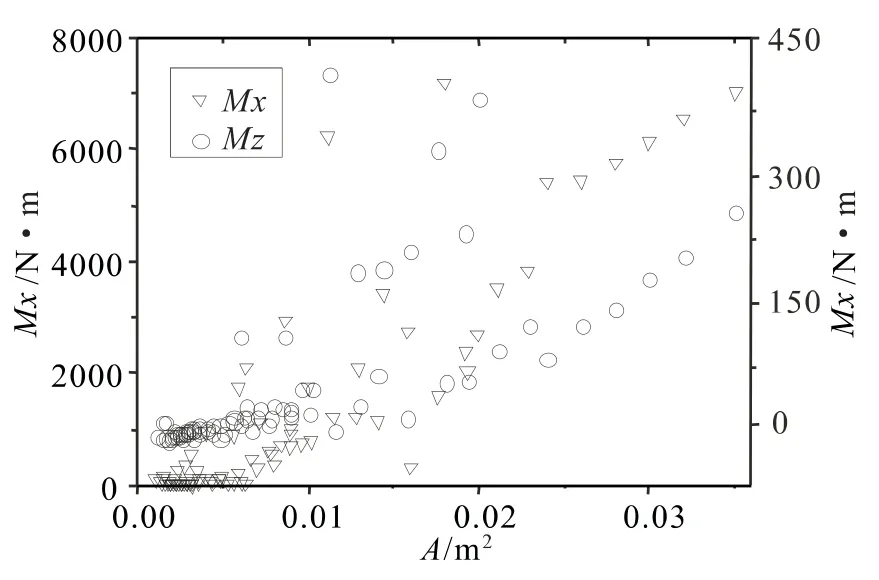
图10 填板横截面弯矩
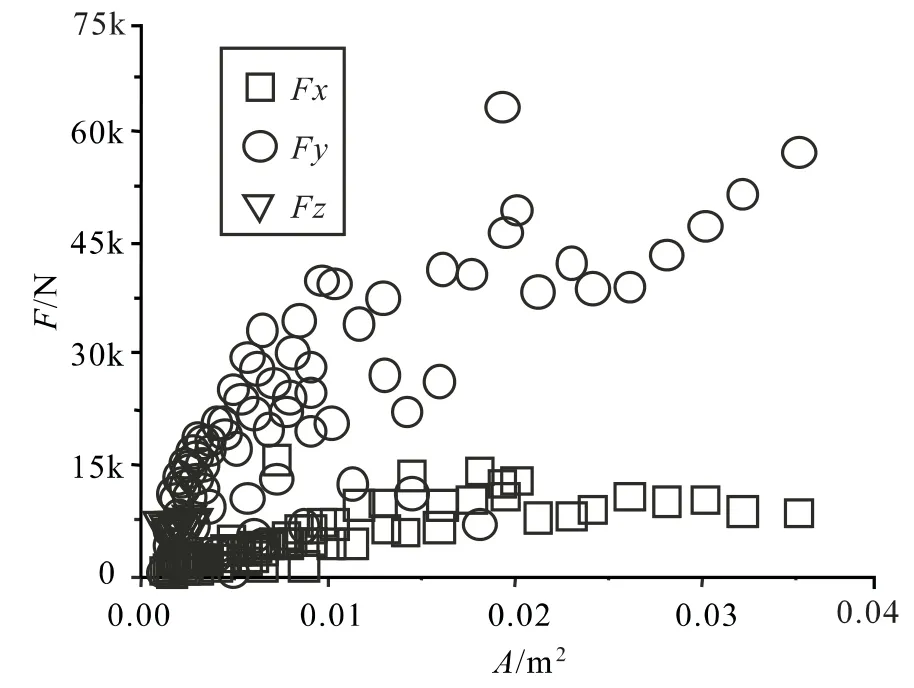
图11 填板横截面轴向力

图12 填板横截面剪力
需要特别说明的是,截面上由法向力积分得到的弯矩Mx(对应规范[7]中的MQ,其计算模型如图13 所示)虽然明显大于Mz,但跟其他几个作用力比是相对小的量;MQ(Mx)对应于截面相对大的抗弯刚度,可知它不起控制作用。同时,规范[7]虽考虑了图13 中Q 方向剪力的作用,但忽略了另一方向横向力的作用。
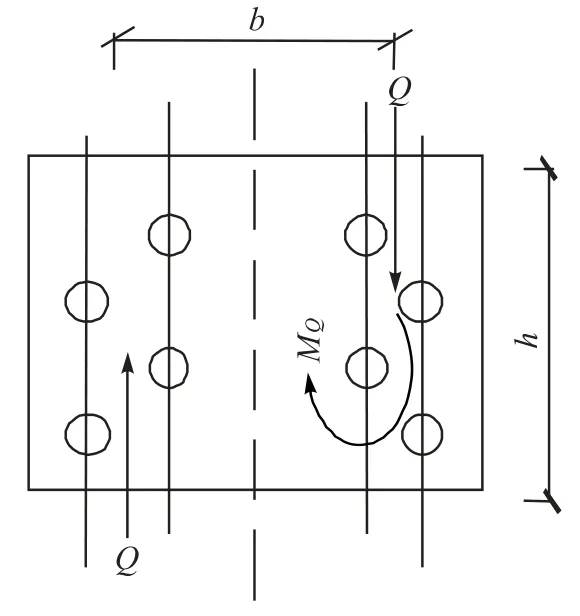
图13 规范计算模型
5 建议的计算方法
综上所述,现有计算规定[6,7]的计算模型与填板实际受力状态存在明显偏差。如果直接偏保守的按通常的构造要求设计填板,又会造成塔重的增加,降低了双角钢构件在实际使用中的优势。因此,得到一个符合填板实际受力状态的计算公式,对填板进行针对性的设计具有显著的意义。
由上述分析可知,填板截面上实际主要受到两个方向的横向力及沿截面法向的轴压力的同时作用,因此建议采用如下公式形式综合考虑各种力的作用效应(坐标系定义见图8):

式中:Np,Mxp,Myp为塑性时填板截面抗力,Ny,Mx,Mz表示填板截面上作用外力的效应,来自本次有限元模型计算结果。
为防止填板发生过大变形,影响双角钢构件承载力和正常使用,由下式作稳定性验算[13]:
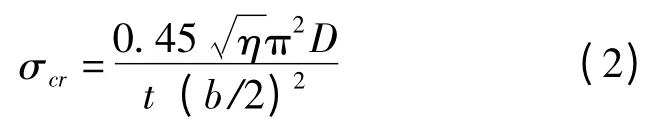
式中:σcr为局部稳定临界应力;η 为切线模量折减,η=0.4;b 为角钢肢宽;t 为填板厚度;D 为板的抗弯刚度,;v 为泊松比,v=0.3。
将式(1)和式(2)联立求得建议的填板厚度。
采用上述建议公式计算填板的双角钢构件与采用构造尺寸填板的双角钢构件(填板间距均按规范[6,7]要求布置)的对比见图14。
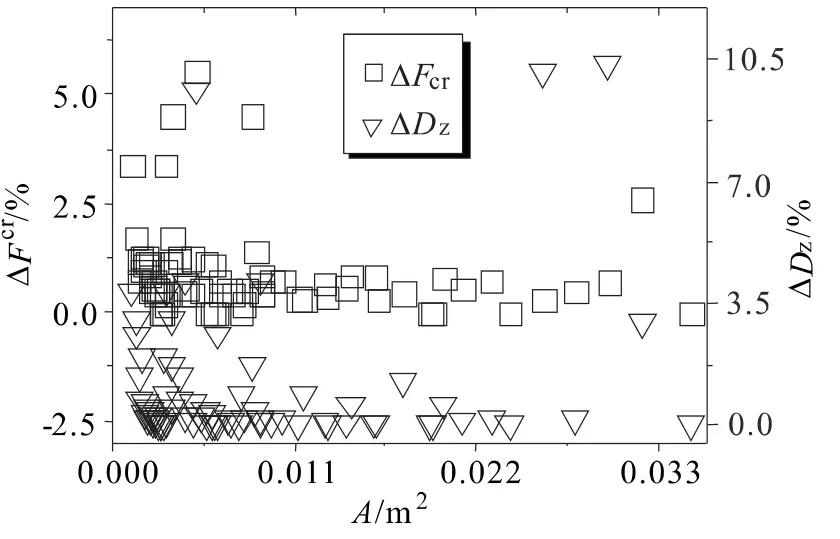
图14 建议公式计算精度
图14 中ΔFcr表示二者临界承载力差值的百分比,ΔDz表示二者达临界力后构件顶部竖向位移差值的百分比。采用建议公式计算的填板,与原构件的临界力平均相差1.5%,总变形(顶部竖向位移)平均相差3%,表明建议公式计算的填板同时满足双角钢构件变形和承载力的要求。
用建议公式计算规范[12]中所有规格角钢对应的双角钢十字截面构件所用的填板,与采用常规构造方法确定的填板的质量进行对比,其质量差值的百分比如图15 所示。计算结果表明,填板质量明显降低,所有规格双角钢构件的填板平均减重19%,肢宽200 mm 及以上双角钢构件的填板平均减重28%。

图15 建议公式优化结果
6 结论
填板是采用组合截面构件时必不可少的连接部件,它不但保证两个角钢协同工作,还对构件总重有明显影响,而现有的填板计算模型和方法,与其实际受力状态存在明显差异。本文从规范[6,7]计算模型和公式出发,以构件试验和有限元计算相结合的方式,详细分析了双角钢构件中的填板,包括填板横截面上应力的分布、种类和特点等,并根据所得结果给出建议的填板计算公式。采用对比计算的方式对建议公式的有效性进行验证,分析了相关参数。上述研究表明,建议的填板计算公式满足双角钢十字截面构件变形和承载力的要求,能有效降低填板重量,具有广泛的适用性。
[1]杨隆宇,李正良,魏磊,等.高强钢管轴压承载力研究[J].西安建筑科技大学学报(自然科学版),2010,42(2):201-204.
[2]齐立忠,江文强,陈大斌.螺栓连接滑移对输电铁塔力学性能的影响研究[J].电力科学与工程,2013,29(3):12-17.
[3]吕健双,李健.特高压输电线路覆冰断线张力计算与分析[J].电力科学与工程,2013,29(8):10-15.
[4]李春曦,王佳,叶学民,等.我国新能源发展现状及前景[J].电力科学与工程,2012,28(4):1-8.
[5]杨隆宇.特高压输电塔组合截面构件承载力理论与试验研究[D].重庆:重庆大学,2012.
[6]GB 50017-2003.钢结构设计规范[S].
[7]DL/T 5154-2012.架空送电线路杆塔结构设计技术规定[S].
[8]左元龙,赵峥,付鹏程,等.大跨越输电铁塔十字组合角钢填板的设计与试验[J].武汉大学学报(工学版),2007,(S1):209-213.
[9]钟寅亥,金晓华.输电铁塔双角钢填板计算方法[J].广东电力,2008,21(3):37-39.
[10]杨利容,郑勇.双角钢十字组合填板设计方法探讨[J].四川建筑科学研究,2010,36(3):32-35.
[11]GB/T 228-2002.金属材料室温拉伸试验方法[S].
[12]GB/T 706-2008.热轧型钢[S].
[13]陈骥.钢结构稳定理论与设计[M].北京:科学出版社,2008.

