含风电机组的电力系统动态经济排放调度研究
黄 兴,杨琳琳,韩 涛,刘啸宇
(国网山东省电力公司 莱芜供电公司,山东 莱芜271100)
0 引言
传统火电机组释放的硫氧化物(SOx)、氮氧化物(NOx)是造成大气污染以及全球变暖的主要原因之一,随着人们环境保护意识的增强和科技的快速发展,绿色可再生能源发电技术在世界范围内得到了广泛的利用,其中最为典型的就是风能发电。相比较于其他可再生能源,风能取之不竭,对环境的影响很小,而且其综合利用成本相对便宜[1,2]。但是,与传统的火电、水电、核电等相比,风电具有很很强的波动性和随机性,且大型风电场基本上都远离负荷中心,风电大规模的接入电力系统后,给传统的电网带来了新的挑战,而且当前对风电场出力的短期预测误差较大[3],加重了系统的调峰调频负担[4,5],使整个系统对旋转备用和非旋转备用需求快速增加,可能会导致系统调度周期内更高的运行费用[6,7]。
传统的电力系统动态经济调度(Dynamic economic dispatch)问题指在一个特定时段内,在考虑预测的负荷需求和系统机组的爬坡率约束,网络约束等条件后,通过优化算法求解出系统中各运行机组的最优出力,从而达到系统运行费用最小的目的[8~11]。但是传统的动态经济调度问题只考虑了使用化石燃料的火电机组等常规机组的运行费用,未考虑由于环境保护条例对火电机组排污的限制,以及在现有含有大规模风电场的电力系统中需要考虑的风电功率特性和风电建设投资给系统优化调度带来的诸多影响。文献[12]研究了在火电机组和风机模型以及随机风电出力的约束条件下,不同风机参数和不同风速下对系统最优调度的影响。文献[13]提出了考虑风电高渗透率的情况下的多目标动态经济调度模型,并提出了一种改进粒子群算法来求解该问题,使系统风险和系统运行费用最小,却没有考虑由于风电波动导致的系统备用补偿容量的变化问题。
本文在考虑传统的动态经济调度模型基础上,提出了包含风电发电成本、火电机组排污的环境补偿成本和系统备用容量补偿成本的动态经济排放调度模型,提出了一种基于水平比较规则的改进差分计划算法(Differential Evolution with Level Comparison,DELC),利用约束度满足度比较解的优劣,最后用算例对本文所提出的模型和算法进行了验证。
1 含风电机组的动态经济排放调度模型
1.1 风电机组出力模型
假设每台风机的型号完全一致,不考虑风机的尾流效应、风机内部的电气损耗,以及风速相关性对整个风电场带来的影响,则风电场的出力为:

式中:Pwi为第i 台风机的输出功率;vin为切入风速;vout为切出风速;Pwi,r为风机的额定功率;N为风机数量。
1.2 风电机组的发电成本
虽然风电为绿色能源,不会消耗化石燃料,但是风电场的前期建设投资成本和后期维护成本巨大,将其折算为风电机组的发电成本:
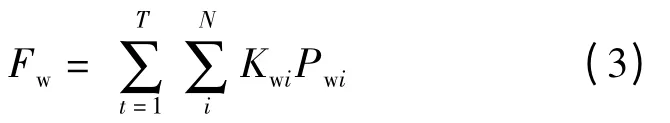
其中:Kwi为第i 台风机的建设维护成本系数;T为时段。
1.3 引入风电后备用容量补偿成本
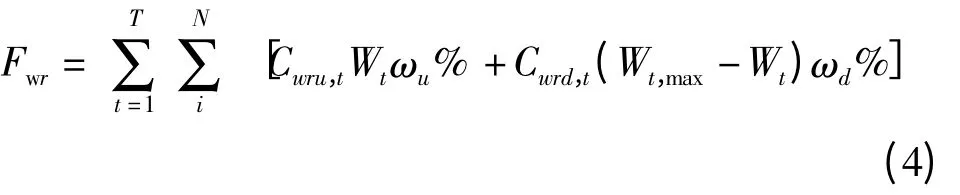
式中:Cwru,t和Cwrd,t分别为系统在t 时段内风电的正负旋转备用容量补偿成本;ωu%和ωd%分别为系统中正负旋转备用的需求系数。
1.4 火电机组的运行成本
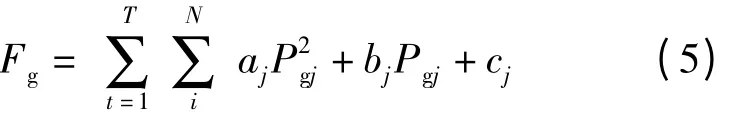
式中:aj,bj,cj分别为火电机组j 的发电成本系数;N 为火电机组的数量。
1.5 火电机组排污的环境补偿成本
火电机组排放的硫氧化合物(SOx)、氮氧化物(NOx)等大气污染物增加了火电机组的环境成本,却能体现不同发电机组的调度优先权。增加火电机组排污造成的环境补偿成本能在不破坏电力系统经济调度运行机制下,合理反映以风电为代表的绿色可再生能源的电能价值,促进风电的发展,其排污特性可通过折算各发电机组的发电量来计算,其所导致的环境补偿成本为:

式中:αj,βj,γj,ηj,δj均为火电机组j 的排污系数。
1.6 目标函数
根据前述内容,含风电机组的经济-排放模型包括4 部分:风电机组的发电成本Fw,系统备用容量补偿成本Fwr,火电机组的运行成本Fg和火电机组排污引起的环境补偿成本Fe,即

1.7 约束条件
(1)忽略系统网损,等式约束条件为:

式中:PD为系统总的负荷。
(2)机组出力约束:

(3)火电机组爬坡率约束:

2 基于水平比较的改进差分进化算法
本文所提出的含有风电的电力系统动态经济调度模型复杂,且约束条件较多,标准的差分进化算法求解该问题时,易陷入局部最优值,对此,提出了一种基于水平比较规则的差分进化算法(DELC),利用约束满足度对得到的解进行比较,从而求出系统最小运行费用。
2.1 标准差分算法
差分算法是一种基于群体进化的智能算法,通过种群内个体间的合作与竞争来实现对优化问题的求解,其基本流程是先随机生成N 个解作为初始种群评价,然后随机选择3 个个体进行变异操作生成临时个体,将临时个体与当前个体交叉生成新个体,再将新个体与当前个体进行比较,选择较好的个体,最后满足终止条件,输出最优解。
2.1.1 变异操作

式中:ui=[ui1,ui2,…,uid]为初始种群;xr1,xr2,xr3为当前种群中随机选择的3 个个体;F 为变异因子。
2.1.2 交叉操作
本文采用二项交叉方式,首先对每个变量生成一个0~1 之间的均匀分布的随机数j,若j <cr,则接受目标个体的对应分量,否则保留当前个体的对应分量,具体如下:

式中:j=1,2,…,d;cr 为0~1 之间的控制新个体和原个体交叉率的正实数;sn 为1~d 之间均匀分别的整数,用于确保至少有一维分量继承于目标个体。
2.1.3 选择操作
水平比较的差分进化算法(DELC)中第t 代种群中的第l 个个体xl,t 与目标个体tl,t 采用水平比较算子,即:

2.2 水平比较
Takahama 和Sakai[14]提出对于函数约束优化问题,一种为每个解定义一个约束满足度的α 约束法来比较解的优劣。
2.2.1 约束满足度
约束满足度为每一个解满足约束的情况,并且可以据此来比较解的优劣。通常,解的约束满足度可用式(1)来描述,可行解的约束满足度为1,不可行解的约束满足度则对于0~1 之间的一个实数。

定义解在每一个不等式约束和等式约束上的约束满足度如下:
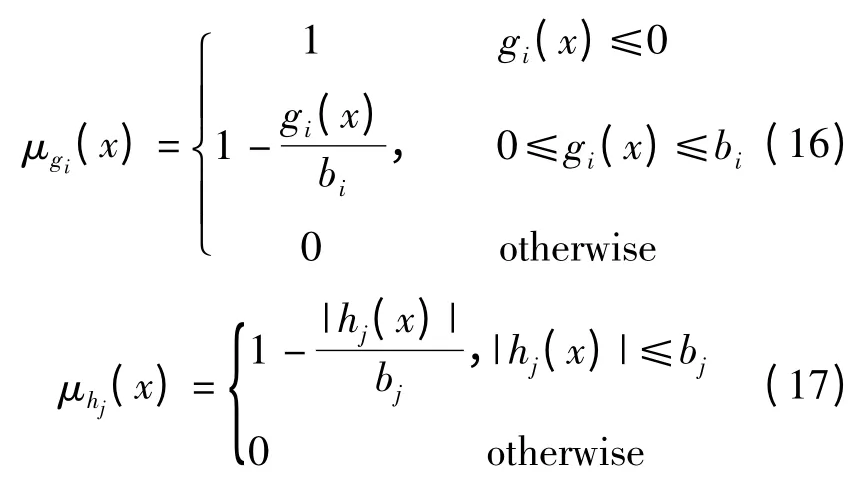
式中:bi,bj为确定约束满足度的参数,为固定的正数;μgi(x),μhj(x)分别表示解x 在不等式约束和等式约束上的约束满足度。
因此,一个解的约束满足度定义为所有等式约束和不等式约束的约束满足度中的最小值,即:
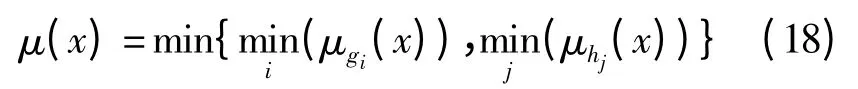
2.2.2 α 水平比较
α 水平比较定义为利用解的约束度和目标函数值,对解的优劣进行比较。设f1,f2和μ1,μ2分别为解x1,x2的目标函数值和约束度,如果任意α 的值满足0≤α≤1,则在(f1,μ1)和(f2,μ2)之间的α 水平值小于等于α 和小于α 时,可以如下定义:

若两个解的约束满足度都大于α 或者相同,则根据解的目标值的大小进行比较,目标值小的解为优;否则,根据解的约束满足度进行比较,约束满足度大的解为优。当α=0 时,仅根据目标值进行比较,完全不顾约束满足度,从而目标值差的不可行解将在与目标值稍差的可行解的比较中取胜;当α=1 时,可行解或约束满足度相等的解将根据目标值进行比较,约束满足度不等的解则根据约束满足度进行比较。因此,为了平衡目标性能和小的违反约束,且使算法在初期强调全局搜索,后期加强对可行域的搜索,本文采用动态调整α 策略,调整规则如下:

式中:t 为进化代数;Gmax为最大进化代数;参数β 用于控制约束满足水平α 的增长速度。图1 为基于水平比较规则的差分进化算法(DELC)流程图。

图1 DELC 算法流程图
3 算例验证
本文在IEEE New England 39 节点(图2)上验证所提出的模型和算法。风电机组额定功率为2 MW,风机数量为100,在21 节点处接入系统,风机的切入风速vi=3 m/s,切出风速vo=25 m/s,额定风速vr=14 m/s,风机的建设维护成本系数Kwi为200 万$ /p.u.,ωu%和ωd%分别为20%和15%,USR为系统中输出功率最大的一台发电机容量470 MW。在DELC 算法中,种群大小设置为100,最大进化代数Gmax=400,变异因子F=0.7,交叉因子cr=0.9,参数β=0.2。
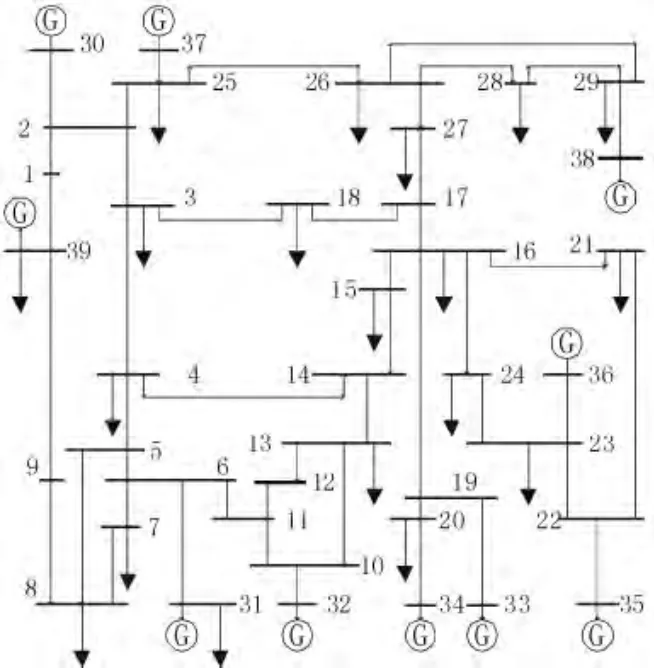
图2 IEEE New England 39 节点
表1 为系统中火电机组的特性参数。

表1 火电机组特性参数
图3 为24 h 内的风电机组出力情况和系统负荷需求情况。可以看出负荷的需求变化情况与总的风电机组出力情况只有部分时段类似,虽然风电机组总的发电功率占整体系统负荷需求的比例较小,仍然可以看出风电出力的反调峰特性明显,增大了系统负荷需求的峰谷差。

图3 24 h 内的风电出力情况和系统负荷需求
图4 为本文所提出的基于水平比较规则的差分算法(DELC)计算后的火电机组日发电量与优化前的比较,从图中可知,优化后的火电机组的出力过程较为均匀,在总发电量增加,满足系统负荷需求的情况下,根据费用最小原则,尽量调度风电机组,减小了火电机组调峰的压力,而且还满足了系统经济性和环境保护的要求,达到整体效益最大的目标。

图4 各火电机组出力对比
图5 为优化前后的火电机组排污所导致的环境补偿成本比较。从图中可以看出,在含有风电机组的电力系统中,由于风电机组的零排放使得火电机组的污染物排放降低明显,降低了火电机组的发电成本,且兼顾了电能生产的经济性和系统排放的低碳性,实现了低碳减排与节省成本的双重目标,减少了环境污染。

图5 优化前后的环境补偿成本比较
表2 为遗传算法(GA)、标准差分进化算法(DE)与本文所提出的基于水平比较规则的差分算法(DELC)的比较,包括发电成本的最小值、平均值、最大值、迭代次数和运行时间。从表中可知,DELC 算法能明显减少算法的迭代次数,能较快地计算出结果,且计算精度均高于GA 算法、DE 算法。虽然DELC 算法使用约束满足程度进行比较,但是其在搜索初期只需知道约束满足程度就可以判定,无需对目标函数进行评价和比较,因此DELC 能够节省计算量,提供算法的搜索效率。
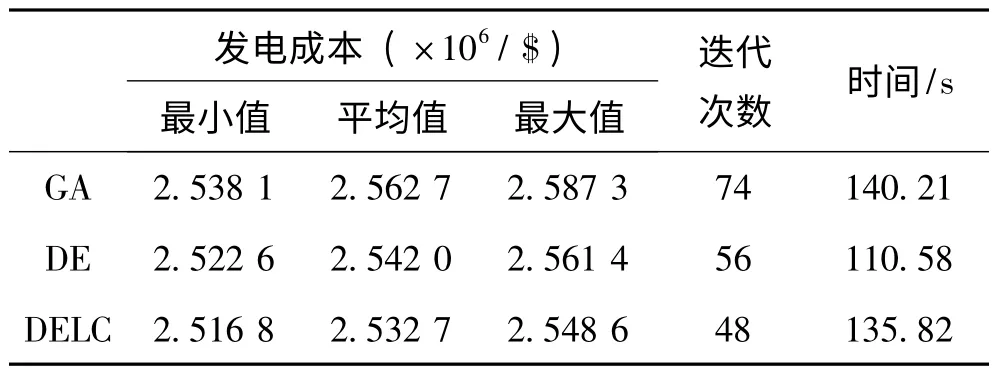
表2 算法比较
4 结论
本文研究了含有风电的电力系统动态经济排放调度问题。在模型建立中,通过计及风电建设的前期投资和后期维护成本,风电波动特性和传统火电机组排位所导致的环境污染问题,引入了风电发电成本、系统备用容量补偿成本和环境补偿成本,建立了动态经济排放模型,该模型在当前风电场大规模上网、环境保护条例日益严格的形式下,对现行的电力系统调度显得愈发重要。在求解该模型时,采用了基于水平比较规则的改进差分进化算法,弥补了标准差分算法易陷入局部最优的缺陷。实例验证了本文所提的模型的合理性和算法的正确性,在实际中具有一定的参考价值。当然,由于条件所限,本文未考虑大规模风电接入后对系统网络安全、机组组合的影响、以及利用需求侧响应消纳风电等问题,这些都值得进一步的研究。
[1]Brendan Fox.Wind power integration:connection and system operational aspects[M].London:the Institution of Engineering and Technology ,2007.
[2]Yazhou L.Studies on wind farm integration into power system[J].Automation of Electric Power Systems,2003,27(8):84-89.
[3]Liu H,Tian H Q,Chen C,et al.A hybrid statistical method to predict wind speed and wind power[J].Renewable energy,2010,35(8):1857-1861.
[4]陈道君,龚庆武,张茂林,等.考虑能源环境效益的含风电场多目标优化调度[J].中国电机工程学报,2011,31(13):10-17.
[5]Ferrer-Martí L,Garwood A,Chiroque J,et al.A community small-scale wind generation project in Peru[J].Wind Engineering,2010,34(3):277-288.
[6]Morales J M,Conejo A J,Pérez-Ruiz J.Economic valuation of reserves in power systems with high penetration of wind power[J].Power Systems,IEEE Transactions on,2009,24(2):900-910.
[7]蒋凌,潘志,成天乐.含风电电力系统旋转备用的鲁棒优化方法研究[J].电力科学与工程,2013,29(4):1-6.
[8]Attaviriyanupap P,Kita H,Tanaka E,et al.A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function[J].Power Systems,IEEE Transactions on,2002,17(2):411-416.
[9]Safari A,Shayeghi H.Iteration particle swarm optimization procedure for economic load dispatch with generator constraints[J].Expert Systems With Applications,2011,38(5):6043-6048.
[10]陈丽媛,陈俊文,李知艺,等.“风光水”互补发电系统的调度策略[J].电力建设,2013,34(12):1-6.
[11]张占安,蔡兴国.考虑碳排放权交易的短期节能调度[J].电网与清洁能源,2012,28(1):60-66.
[12]Liu X.Economic load dispatch constrained by wind power availability:A wait-and-see approach[J].Smart Grid,IEEE Transactions on,2010,1(3):347-355.
[13]Wang L F,Singh C.Balancing risk and cost in fuzzy economic dispatch including wind power penetration based on particle swarm optimization[J].Electric Power Systems Research,2008,78(8):1361-1368.
[14]Takahama T,Sakai S.Constrained optimization by applying the α constrained method to the nonlinear simplex method with mutations[J].Evolutionary Computation,IEEE Transactions on,2005,9(5):437-451.

