太阳能换热系统的机理建模及研究

曹丁元，金秀章，孙小林，谢泽坤

(华北电力大学 控制与计算机工程学院，河北 保定071003)

0 引言

近些年环境污染、资源短缺一直是人们讨论的热门话题，具有无污染、可再生、经济、清洁等优点的太阳能成为专家学者的研究对象。西安交通大学的魏进家教授提出了复合抛物面聚光器(CPC)型太阳能光伏/光热联合利用(PV/T)系统［1］。采用CPC 聚光器的光电和光热相结合的PV/T 系统，当聚光比确定后，影响系统性能的主要参数是太阳电池的工作温度。因此，确定太阳电池的工作温度对于系统设计具有指导意义。目前为止，国内外很多学者对CPC-PV/T 系统的性能分析进行了不少研究［2～6］，但是涉及CPC-PV/T 综合系统中太阳电池温度的建模报道尚少。本文将对系统中太阳电池工作温度的机理模型建立进行讨论。机理建模［7］是在充分了解了受控对象、执行机构及系统内一切元件的运动规律，将这些运动规律用数学模型表示出来的过程。机理建模一直以来广泛应用于各个领域［8，9］，具有理论依据严密，在任何状态下使用都不会引起定性错误的优点。

1 数学模型分析

CPC-PV/T 系统简图如图1 所示，它主要由两部分构成:太阳能光电系统以及太阳能换热系统。太阳能光电系统是PV 电池板接收到来自聚光器的光照而产生电能的系统;太阳能换热系统是下层流道中的流体吸收PV 电池板的废热，从而使电池板温度处在最佳工作点，同时产生可利用的热能的系统。本文主要对太阳能换热系统的模型进行分析。

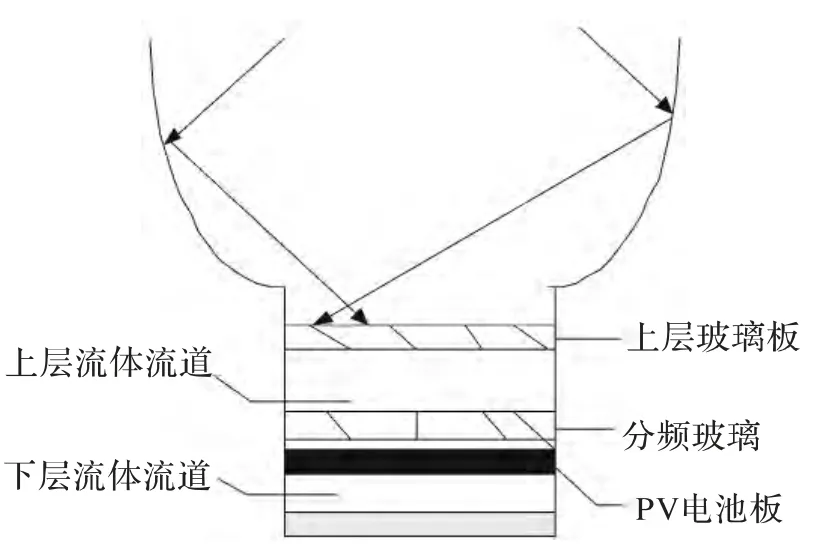
图1 CPC-PV/T 系统简图

电池板的温度主要受太阳辐射和下层流体流量的影响。太阳辐射照射到光伏电池上，会使电池板的温度升高，从而影响到系统的光电效率。为了降低电池板的温度，使其处在最佳的工作温度下，本课题采用了平板PV/T 集热器，当下层流体流过电池板，带走电池板的废热，即降低了电池板的温度，又提高了流体的温度，实现了热量的充分利用。

对于下层流体与电池板的热交换部分，建模方法分为集总参数建模法［10，11］和分布参数建模法［11，12］。在流体与电池板导热过程中，流体与电池板的状态参数不仅是时间而且还是空间的函数，具有明显的分布参数特点。这种分布参数的动态模型都是非线性偏微分方程组，这些偏微分方程组含有长度和时间两个自变量。这样一个分布参数系统的非线性模型是十分复杂的，计算也有一定难度。为了简化问题，在建立数学模型时，将下层流道内的介质状态参数看成是均匀一致的，并在空间位置上选定一个有代表性的点，利用这一点介质的参数作为环节的集总参数。在这种简化假定下建立的模型就是集总参数模型。

为了便于分析，需要对换热管道作几个合理的简化假设:

(1)电池板无轴向导热;

(2)下层流道内液相介质为不可压缩流体;

(3)忽略流体的轴向传热;

(4)电池板与下层流道的换热系数为常数;

(5)同一横截面的流体的参数相同;

(6)电池板沿下层流道长度方向的放热量均匀。

1.1 分布参数建模

电池板与下层流道简图如图2 所示，在上述简化假设条件下，可列出距入口x 处的微分流道段dx 中在单位时间内的热平衡方程如下:

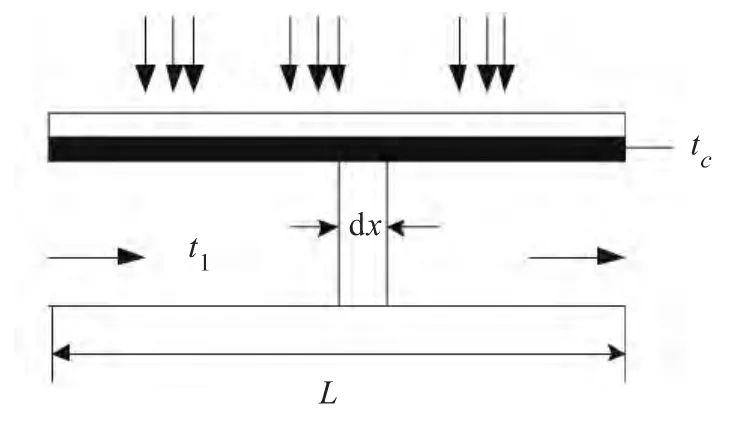
图2 电池板与下层流道简图

下层水热平衡方程为:

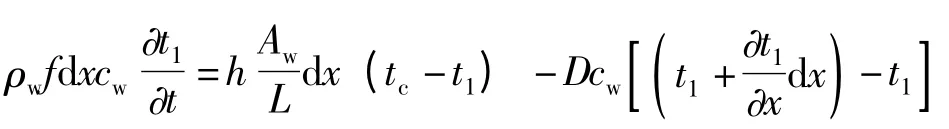
式中:ρw，cw，t1分别为下层水的密度、比热容、入口温度;tc为电池板的温度;Aw为流体流道换热面积;f 为流体流道内横截面积;h 为电池板导热系数;L 为电池板长度;D 为下层流体的质量流量。上式整理后得

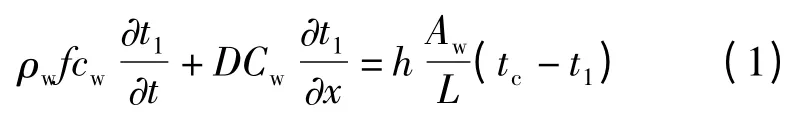
对于电池板，其能量平衡方程为:

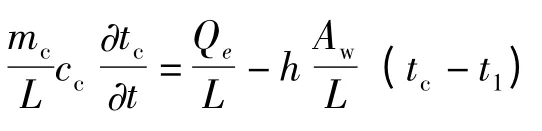
式中:mc，cc分别为电池板的质量和比热容。

电池板吸收的太阳辐射的热量:

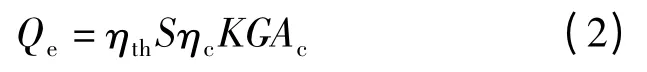
式中:ηth为光伏电池光热转换效率;S 为玻璃盖板对太阳光的透射率;ηc为分频玻璃的分频效率;k 为聚光比;Ac为电池板的面积;G 为太阳辐射强度，可测量。

将(2)式代入上式，整理后得

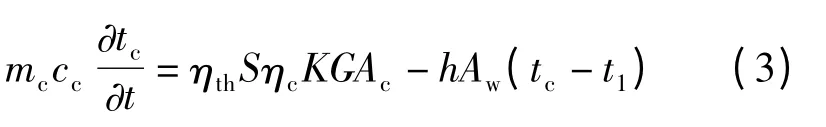
电池板的温度变化的原因可以来自于下层流道流体的流量(流体的初始温度为恒定值)或者光照强度。在不同的扰动下，电池板温度的动态特性是不同的。文献［13～15］等分别针对不同的扰动因素，通过拉普拉斯(Laplace)变换，求出方程组的解析解。本文对不同扰动同时发生求出解析解。

对式(1)、(3)两式化为增量形式，然后进行二元拉氏变换，消去中间变量Δt1(x，s)得:

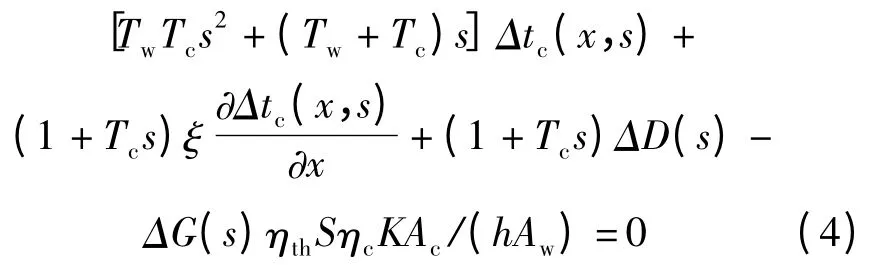
对(4)式进行求解得到电池板初始温度、流量和光照强度3 项扰动同时存在时的叠加响应为:

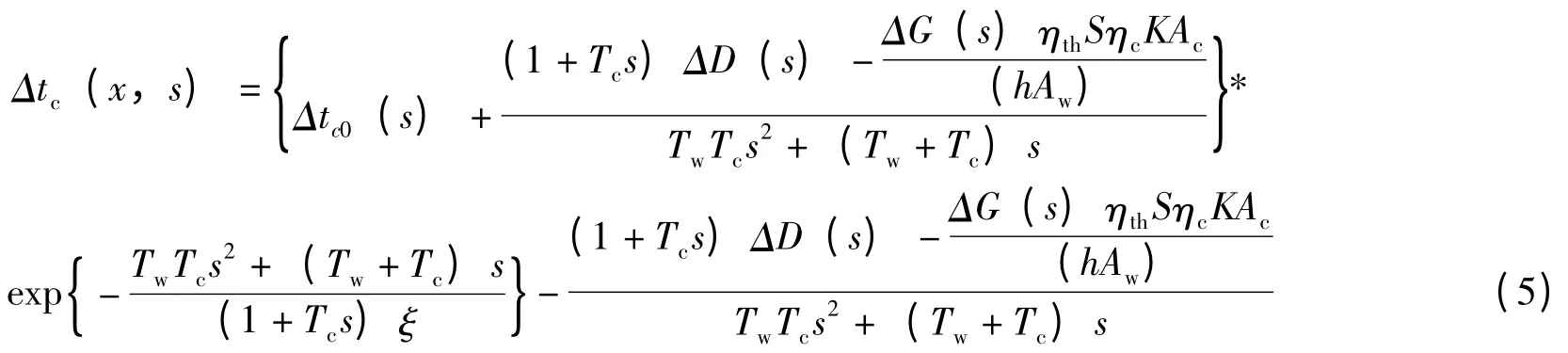
式中:tc0(s)为电池板初始温度。

为了得到各个扰动对系统的独立作用，分别令其他两个扰动为零。对于初始温度扰动，令D(s)=0，G(s)=0，最后得到其传递函数为

同理，可以得到太阳光照强度ΔG(s)和水工质流量ΔD(s)扰动下的传递函数分别为

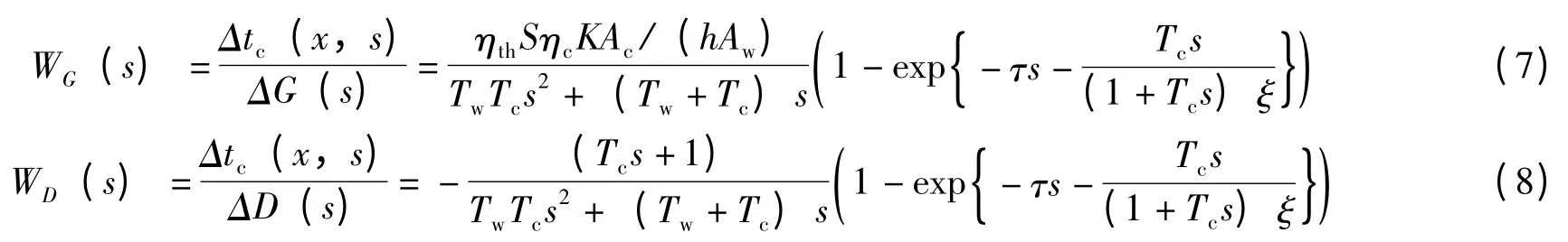
由于式(6)～(8)均为超越型传递函数。计算起来很不方便，因此，采用低阶逼近将它们进行简化［2，3］。具体方法是将上述传递函数在s=0 附近的领域内展开为泰勒级数的形式，并与假设的传递函数相应的展开式进行比较，从而确定假设的传递函数的各项数。

假设各个扰动下的传递函数为

2017年，IPO审核加速带动了创投基金的募集、投资和退出，政府引导基金的进一步扩容引导了社会资金更多地流进创投基金和实体经济，港股、美股的窗口期为具有国际视野的创投基金带来更大的机会，整个中国创投行业呈现出良好的发展态势。无疑，创投行业的快速发展，已经成为破解中小企业“融资难”问题、加快金融供给侧改革的重要手段。

对于电池板初始温度扰动，将式(6)与式(9)均在s=0 点处展开泰勒级数，取其前三项相等得到式(9)的系数分别为:，T。指数n 总是四舍五入取整数。

对于太阳光照强度G 扰动，将式(7)与式(9)均在s=0 点处展开泰勒级数，取其前三项相等得到(9)式的系数的系数分别为:K=。指数n 总是四舍五入取整数。

对于水工质流量d 扰动，将式(8)与式(9)均在s=0 点处展开泰勒级数，取其前三项相等得到式(9)的系数分别为:，n=2，T。指数n 总是四舍五入取整数。

1.2 集总参数建模法

水的能量平衡:

式中:Qi为水与电池板之间的换热量;t1，t2分别为水的进出口温度。

电池板对水的放热量:

式中:tc为电池板的温度。

电池板的能量平衡方程:

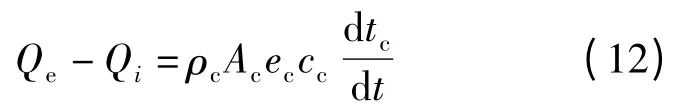
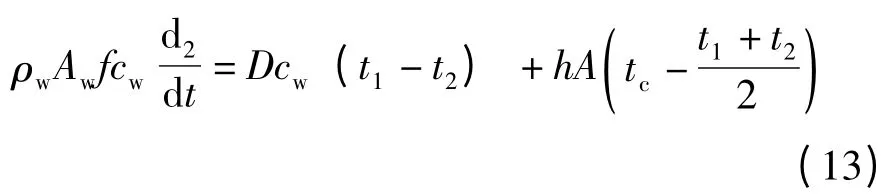
由式(2)、(11)、(12)可得:

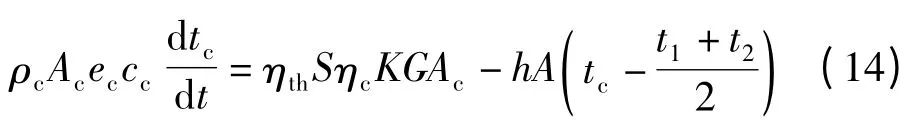
对上述式(13)、(14)分别作拉氏变换，经推导得温度、流量和光照强度扰动的传递函数模型:

电池板初始温度扰动:

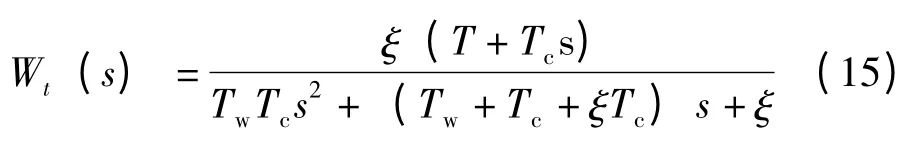
水工质流量D 扰动:

太阳光照强度G 扰动:

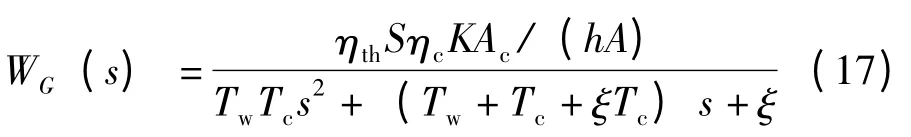
2 模型仿真与分析

根据表1 中的原始数据和简化结果得到分布参数模型在各个扰动下的传递函数为:

表1 参数物理意义

电池板初始温度扰动:

太阳光照强度扰动:

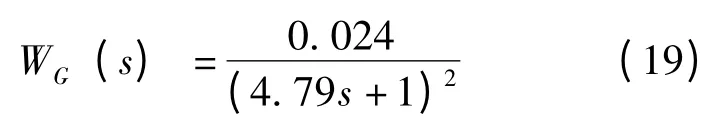
水工质流量扰动:

根据表1 中的原始数据和式(15)～(17)得到集总参数模型在各个扰动下的传递函数为:

电池板初始温度扰动:

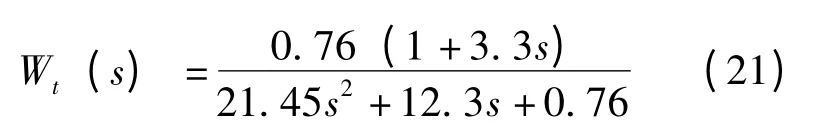
太阳光照强度扰动:

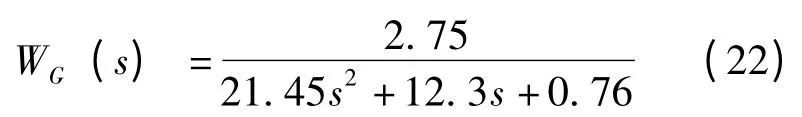
水工质流量扰动:

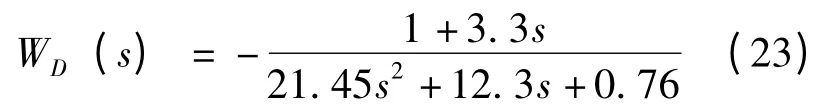
求取以上各传递函数的阶跃响应曲线，如图3，4，5 所示，(a)图均为分布参数模型，(b)图均为集总参数模型。由图3 可以看出，当光照强度增加1 W/m2，电池板的温度大约增加0．024 K;由图4 可以看出，当流体流量增加1 kg/s，其他扰动为零时，电池板温度下降大约1．35 K;由图5 可以看出，当电池板初始温度增加1 K，其他扰动为零时，电池板最终温度在一定的时间范围内上升1 K。综上，当光照强度增加时电池板的温度会升高。当流体的质量流量增加时，会带走更多的热量，从而电池板的温度会有所下降，由此可判断流量越快，电池板降温越快。当电池板的初始温度发生变化的时候电池板的最终温度会变化相同的幅度。对比分布参数模型和集总参数模型的曲线可以看出分布参数模型能更好地反映系统的动态性能，但是分布参数法计算复杂。

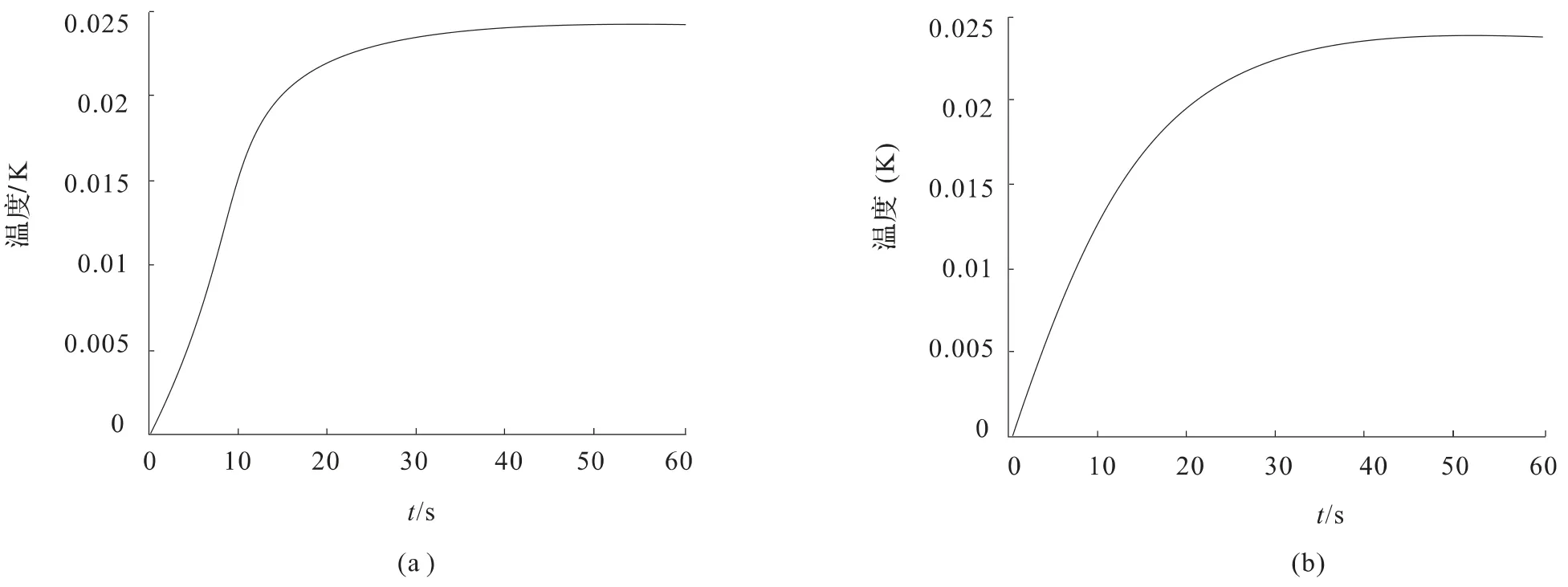
图3 电池板温度在光照强度扰动下的响应

图4 电池板温度在流体流量扰动下的响应

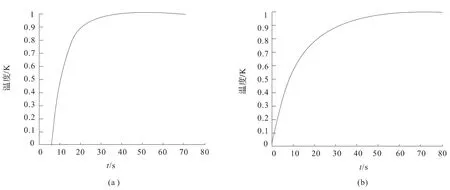
图5 电池板温度在初始温度扰动下的响应

3 结论

通过对复合抛物面聚光器(CPC)型太阳能光伏/光热联合利用(PV/T)系统生产工艺的研究，本文利用能量守恒定律得出了PV/T 系统的分布参数模型和集总参数模型，分别给出了在不同扰动下电池板温度的传递函数，并且进行了仿真。仿真结果表明，这两种机理建模方法都能够很好地反映系统的动态性能。由模型可以看出，流体流量是控制电池板温度在最佳工作点的主要因素。机理模型的确定为CPC-PV/T 系统的进一步优化奠定了理论依据，为CPC-PV/T 系统控制算法的研究提供了技术支撑。

［1］魏进家，谢胡凌，敬登伟．一种太阳能聚光分频光伏光热联产装置［P］．中国专利．CN201210224815．9，2012．

［2］刘亚雷，张红，许辉，等．CPC 型聚光光伏光热系统的性能分析［J］．可再生能源，2011，29(1):1-5．

［3］崔文智，于松强，廖全．聚光型混合光伏光热系统热电性能分析［J］．重庆大学学报，2009，32(1):86-90．

［4］孙健，王艳香，施明恒．复合抛物面聚光太阳能PV/T 系统的实验研究［J］．太阳能学报，2012，33(1):86-91．

［5］Amrizal N，Chemisana D，Rosell J I．Hybrid photovoltaic-thermal solar collectors dynamic modeling［J］．Applied Energy，2013，101:797-807．

［6］Mohd Yusof Hj Othman，Baharudin Yatim，Kamaruzzaman Sopian，et al．Performance analysis of a double-pass photovoltaic/thermal(PV/T)solar collector with CPC and fins［J］．Renewable Energy，2005，30(13):2005-2017．

［7］韩璞，董泽，王东风，等．智能控制理论及应用［M］．北京:中国电力出版社，2012．

［8］李雅哲，塔式太阳能热发电蒸汽系统建模与控制［D］．北京:华北电力大学，2011．

［9］马进，刘长良，李淑娜．稳压器压力水位控制系统建模与仿真［J］．核科学与工程，2010，30(1):9-14．

［10］康英伟，薛阳，黄伟．电站锅炉过热器的集总参数动态建模与仿真［J］．计算机仿真，2012，29(9):332-334．

［11］阮刚，罗自学，周怀春．锅炉过热蒸汽温度控制新策略动态仿真研究［J］．华中电力，2004，17(5):1-4．

［12］周少祥，胡三高，宋之平．管式换热器分布参数模型的分段线性化方法研究［J］．中国电机工程学报，2002，22(6):123-125．

［13］李旭．蒸汽发生器的动态特性——模型、结构参数的影响和控制［D］．北京:清华大学，1988．

［14］倪维斗，徐向东，李政，等．热动力系统建模与控制的若干问题［M］．北京:科学出版社，1996．

［15］(美)E0．道别林，童钧芳．系统的建模和响应—理论及实验方法［M］．关国枢译．上海:科学技术文献出版社，1984．