一种高精度的嵌入式大气数据传感系统算法

周国昌, 李清东, 郭阳明

大气数据是指大气层内飞行器的攻角、侧滑角、动压、静压、马赫数、真空速、气压高度及高度差等数据。准确测量大气数据对于现代飞行器的飞行控制、导航和事后分析均有十分重要意义[1]。传统基于空速管进行飞行器大气数据的测量已不能完全满足现代飞行器发展的要求。美国航空航天局在20世纪60年代就开始研制嵌入式大气数据传感系统(flush air-data sensing system,FADS)。FADS利用安装于飞行器表面的测量气压的压力传感器阵列,测量飞行器表面的压力分布,根据飞行器表面压力与大气数据构建的压力数学模型,求出动压、静压、迎角以及侧滑角等飞行中所关心的大气数据[2],并将其传送给飞行器的控制系统。FADS的测量精度高,可以应用在高马赫数、大迎角的飞行条件下。目前,已被广范应用于F/A-18、X-33、X-34、X-43a等各型现代飞行器上。

FADS系统的压力模型是一个非线性函数,用非线性衰减的最小二乘法可以解算。但是,最小二乘法由于迭代的问题,在算法稳定性上有不足之处。为此,X-33的FADS系统发展了一种所谓triples的算法,即三点法[3]。该算法最大的优点是可以直接计算迎角和侧滑角,从而得到流体的入射角;进而再计算得到动压、静压和马赫数。但是,在实际的测量系统中,任一环节会具有非线性特性,均需要通过非线性校正方法实现测量系统输人与输出的理想关系。而且,在计算侧滑角的过程中,三点法还会出现奇异值问题。神经网络具有强大的非线性映射能力,可以拟合FADS系统的非线性数学模型,减少输入向量的维数和网络训练难度,可以完成测量校正。另外,采用广义逆方法可以避免传统方法计算量大、收敛性和稳定性分析困难的不足。因此,本文提出了一种基于广义逆与BP神经网络相结合的FADS算法。该算法不但可以克服以上不足,而且还具有一定的容错能力,可有效地保证输出数据的精确性和可靠性。

1 相关知识

1.1 FADS数学模型

FADS系统一般安装在飞行器的头部, 也有安装在机翼两侧的。下面以X-33的FADS系统为例进行讨论。该系统是典型的FADS系统,安装在X-33的球形头部,采用6个压力传感器测量头部表面的压力分布。其压力传感器布局如图1所示。

图1 X-33的FADS测压点布局

文献[4]中,给出了图1中FADS表面压力数学模型

(1)

式中:pi表示传感器第i个测压孔的压力测量值;qc表示动压;P∞表示静压;ε为形压因数,与压缩效应、气动外形、系统影响等因素有关,ε为迎角、侧滑角和来流马赫数的函数,其函数关系是在飞行之前通过风洞试验等手段确定;θi为入射角,该点的表面法线方向与来流速度矢量的夹角,是迎角α、侧滑角β和压力传感器的位置角(圆周角φi、圆锥角λi)的函数

(2)

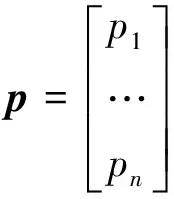
p=Hx

(3)

p为测压点压力测量值向量,H为测压点安装矩阵,当迎角、侧滑角已知时H也已知,x是关于静压、动压的变量。

1.2 BP神经网络

BP神经网络是一种以函数逼近理论为基础的前馈神经网络,具有训练速度快、最佳逼近性能的优点,常用于函数逼近等领域[5]。BP神经网络结构是由输入层、隐含层和输出层组成。本文中隐含层采用径向基函数作为网络的激活函数。径向基函数是一个高斯型函数,它是将该层权值矢量w与输入矢量p之间的矢量距离与偏差b相乘后作为网络激活函数的输入[6]。只要隐含层有足够的神经元,网络则能以任意期望的精度逼近任何函数。典型的BP神经网络结构如图2所示。

图2 BP神经网络结构图

通常,BP神经网络隐含层节点数设定与输入p中的样本组数相同,且每个隐含层中的权值w1被赋予一个不同输入矢量的转置,以使得每个神经元都作为探测器。

2 基于广义逆的容错求解算法

令矩阵A的Moore-Penrose广义逆矩阵为[7]

(4)

式中:V、U为酉矩阵,∑为对角阵。安装矩阵H的秩rankH=2,可以使用Moore-Penrose广义逆矩阵求解x,即

x=H+p

(5)

考虑到压力传感器的测量误差,其真实值与测量计算值之间的误差可表示为

(6)

(7)

H+(H+)T=V∑-2VT

(8)

式中:λ1、λ2是安装矩阵H的特征值。由(8)式可知,广义逆方法的计算结果误差受H+(H+)T的影响,通过配置安装矩阵H,广义逆方法可以有效降低测量噪声ξ的影响,提高计算精度。同时,Moore-Penrose广义逆矩阵方法是建立在奇异值分解基础上的矩阵求逆方法,当A发生列秩亏损时,也可给出最小二乘解。因此选择广义逆进行最小二乘求解,可得到如下的关于动压qc、静压P∞的关系式

(9)

为了确保在各压力传感器发生故障时计算的正确性,本文考虑在广义逆运算中加入故障检测和诊断结果Q,使得算法具有容错能力,其算法过程如下。

由(1)式可以得到(9)式,pi、pj、pk表示FADS中任意3个压力传感器的测量值

(10)

根据(10)式可以写出奇偶校验方程

(11)

利用奇偶校验方程式(11),可以实现对FADS各压力传感器的故障检测与诊断。

若设Q=diag(a1,a2,…,an)是对角线元素值为1或0对角矩阵,其中ai=1或0,i∈[1,n]。则当故障检测与诊断环节确定测压点i出现故障或测量值异常时,ai取值为0,其余正常的测压点对应的对角线元素取1。将Q代入到(8)式中,可得到具有容错能力的广义逆计算公式

(12)

3 基于BP神经网络的校正

实际飞行环境中,气流流动会受机体诱导的上洗和侧洗的影响,从而改变当地的流动角,即机头表面压力传感器所测得的是气流在飞行器头部的当地迎角αe,而不是来流真实迎角α。αe和α之间,βe和β之间有以下关系

α=αe+δα

β=βe+δβ

(13)

式中:δα、δβ分别为迎角和侧滑角的修正量,它们可以通过风洞试验和飞行试验校准。在研究初期,通常采用计算流体动力学计算数据代替试验数据。

(14)

于是,马赫数求解模块的计算方法和训练样本可生成如下

(15)

而qc、P∞、M∞之间存在确定的函数关系

(16)

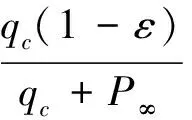
M∞=f(qc(1-ε),qc+P∞,αe,βe)

(17)

在动压修正比、迎角和侧滑角已知的条件下,可以求解出唯一确定的马赫数。获得马赫数M∞及由广义逆计算得到的qc+P∞值后,则可以分别得到静压、动压值如下

qc=(qc+P∞)-P∞

(18)

4 基于广义和BP神经网络的FADS算法

融合广义逆和BP神经网络的FADS算法流程如图3所示,概述如下:

1) 应用三点法对经过延迟补偿的测量值进行计算,预估当地迎角和当地侧滑角;

2) 采用奇偶校验法综合利用各压力传感器测量值进行故障检测与诊断;

3) 用广义逆矩阵求取总压、修正动压之后,使用BP神经网络求解马赫数;

4) 求解出动压、静压、真实迎角和真实侧滑角。

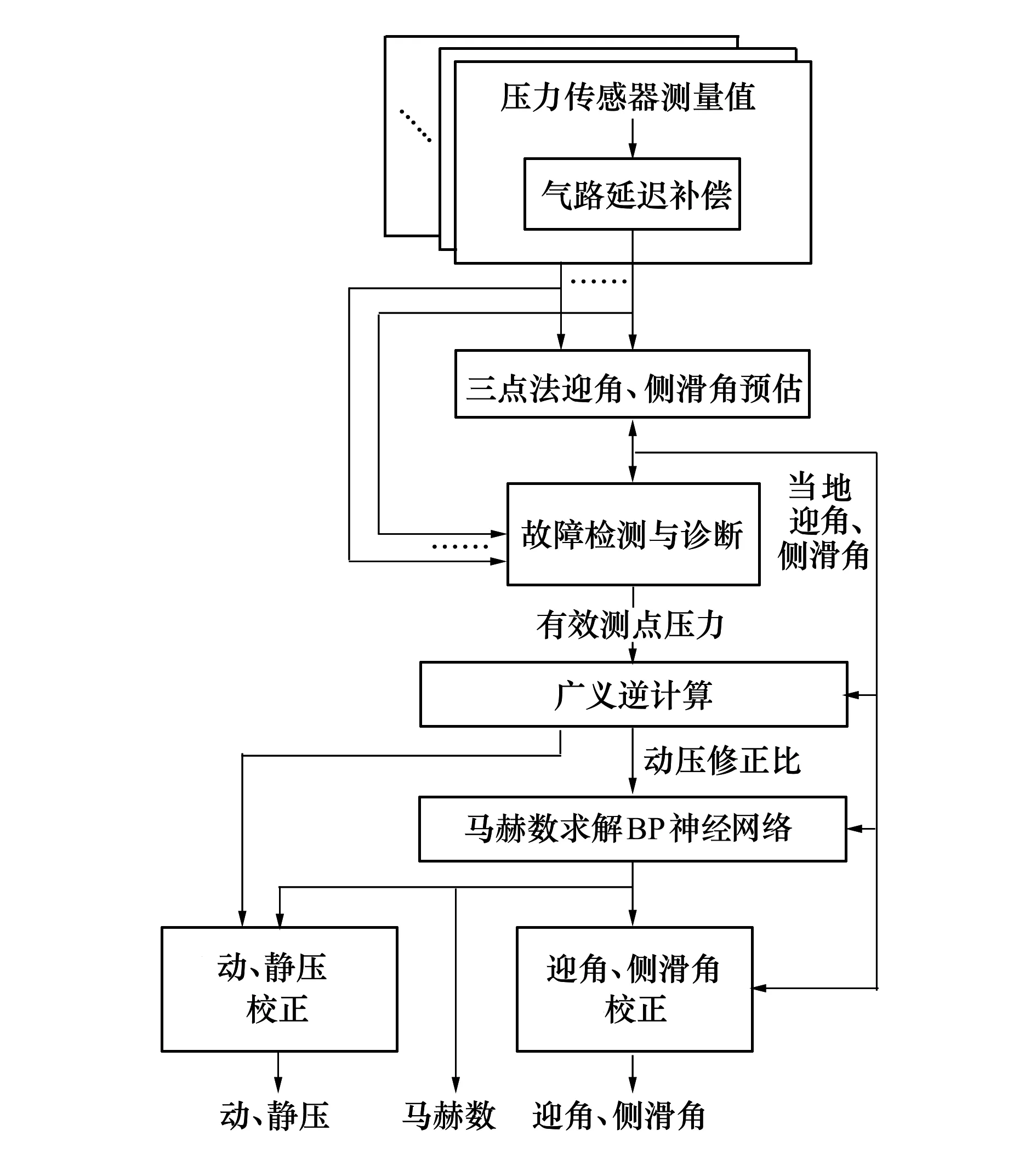
图3 融合广义逆和BP神经网络的FADS算法流程

以上算法流程中包括马赫数求解BP神经网络、迎角校正BP神经网络、侧滑角校正BP神经网络3个BP神经网络模块。

5 算法分析

选择3组弹道飞行数据的迎角、侧滑角作为试验数据,利用1976年美国标准大气表反求文献[4]中X-33的FADS布局中的6个测压点的压力值,并加入3 m/s的风速干扰和10%的大气密度偏差,设压力传感器的测量误差在0.1%以内,根据计算值随机给出误差小于0.1%的数值作为压力传感器的测量值。设计3层结构的BP神经网络,利用压力传感器测量值完成训练以及马赫数、校正迎角和侧滑角的计算,进而解算出大气数据。3组BP神经网络的训练测试结果如表1所示。

表1 3组BP神经网络测试结果表

本文FADS算法的计算结果如表2所示。

表2 算法解算结果误差表

由表1、表2可以看出,在不考虑其他误差的条件下,计算结果与模拟数据吻合的程度非常好,其结果的动压误差远远小于文献[4]算法的误差值718 Pa,迎角和侧滑角的误差远远小于文献[4]算法的误差值0.5°。在实时性上,采用本算法计算马赫数所需的时间小于迭代算法的10%,能满足大气参数刷新速率0.05 s的要求。仿真结果表明,本文算法计算精度高,解算速度快。

6 结 论

本文提出了一种利用广义逆和BP神经网络相结合的FADS算法。该算法基于故障检测与诊断的结果,实现了具有容错能力的广义逆计算。同时,计算的大气数据经过BP神经网络校正,精度进一步提高。所提新方法弥补了原有单一方式的FADS算法的不足,具有更好的应用前景。

参考文献：

[1] Cobleigh B R,Whitmore S A,Haering E A. Flush Air Data Sensing (FADS) System Calibration Procedures and Results for Blunt Fore-Bodies[R]. California: Dryden Flight Research Center Edwards,1999

[2] Jost M, Schwegmann F, Köhler T. Flush Air Data System——An Advanced Air Data System for the Aerospace Industry [R]. AIAA-2004-5028, 2004

[3] Ian A Johnston, Peter A Jacobs. A Study of Flush Air Data System Calibration Using Numerical Simulation[R]. AIAA-1998-1606,1998

[4] Whitmore S A, Cobleigh B R, Hearing E A. Design and Calibration of the X-33 Flush Airdata Sensing (FADS) System[R]. NASA/TM-1998-206540, 1998

[5] Moody J, Darken C. Fast Learning in Networks of Locally-Turned Processing Units[J]. Neural Computation, 1989(1): 281-294

[6] Broomhead D S, Lowe D. Multivariable Function Interpolation and Adaptive Networks[J]. Complex System, 1988(2): 321-355

[7] Albert A. Regression and the Moore-Penrose Pseudoinverse[M]. New York: Academic Press,1972