基于多群体改进萤火虫算法的UCAV协同多目标分配

王永泉, 罗建军

现代战争中，随着战场环境和战术任务日趋复杂，无人作战飞机(unmanned combat aerial vehicle，UCAV)协同作战已成为未来信息化战争发展必然趋势[1]，多机型无人机协同使用，将在整个作战过程中发挥重要的作用[2]。合理分配兵力资源以获取最大的打击效果是发挥UCAV协同攻击效果的关键[3]。

目前，学者们陆续提出了UCAV协同攻击目标分配算法，对UCAV协同攻击实战应用具有一定意义。文献[4]通过运用整数线性规划法，给出了目标分配最优方案，但是算法模型复杂，计算量较大。文献[5]在博弈论基础上，提出了基于博弈论的目标分配算法，但是算法实时性值得考虑。文献[6]基于动态任务分配问题，提出一种改进的混合再次分配策略，但该方法本质上还属于静态多目标分配范畴。随着智能启发式计算技术的发展，智能优化算法已开始应用于UCAV协同攻击目标分配问题中，并提供了新的研究思路[1]。

萤火虫优化(glowworm swarm optimization，GSO)[7]算法源自于自然界中萤火虫飞行的生物学现象，具有运算速度快、容易实现、调节参数少等特点[8]，并被成功应用于复杂函数优化及工程技术领域中。本文在分析协同多目标分配问题的基础上，重新设计萤火虫离散编码方式，并给出适合离散编码的萤火虫更新策略。对于基本GSO收敛效率不高的缺陷[8]，提出具有多群体性的改进萤火虫优化(multi-intelligence improved glowworm swarm optimization，MIGSO)算法：引入局部搜索及全局信息交换机制，并将萤火虫优化算法与混合蛙跳算法融合，实现多智能群体共同进化。最后，利用MIGSO算法求解UCAV协同多目标分配数学模型，进而得到最优分配方案。

1 UCAV协同多目标分配数学模型

本文以UCAV执行空对地打击任务为背景，并已通过侦察手段获取蓝方目标信息。设红方共有m架UCAVU={Ui,i=1,2,…,m} (Ui表示第i架无人机)，蓝方共有m个目标T={Tj,j=1,2,…,n} (Tj表示第j个目标)。设oij为决策变量，oij=1表示目标Tj分配给Ui；oij=0表示目标Tj不分配给Ui。UCAV协同攻击目标分配以作战效能取得最优为目标，而收益指标、消耗指标及航程指标是评价作战效能的主要指标[9]。

定义1 收益指标 当UCAV协同攻击全部目标后，红方无人机获得价值Ewin最大。

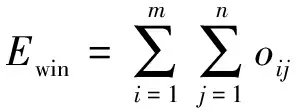
(1)

式中：Pij表示Ui攻击Tj时的杀伤概率,Qj表示Tj的价值。

定义2 消耗指标 当UCAV协同攻击全部目标后,红方无人机消耗价值Eloss最小。

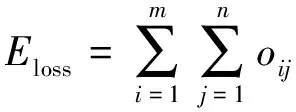
(2)

式中：Wij表示Ui攻击Tj时的生存概率,Vi表示Ui的价值。

定义3 航程指标 当UCAV协同攻击全部目标后,红方无人机总航程D最小。

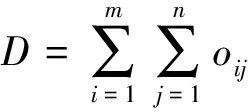
(3)

式中：Dij表示Ui攻击Tj时飞行航程。

定义4 目标函数 UCAV协同多目标分配目标函数f(xij)定义为:

maxf=ω1·Ewin-ω2·Eloss-ω3·D

(4)

式中：ω1、ω2、ω3为权重系数,分别反映了不同指标重要程度。

约束条件:

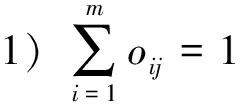
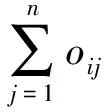
2 多群体性的改进萤火虫(MIGSO)算法

2.1 基本萤火虫优化(GSO)算法及改进

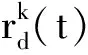
lk(t)=(1-ρ)lk(t-1)+γf[Xk(t)]

(5)

式中：ρ∈(0,1)为荧光素挥发因子,γ∈(0,1)为荧光素更新率。萤火虫位置采用轮盘赌的方式进行,其可以描述为:

(6)

(7)

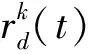
(8)

式中：β为决策范围更新率,Nt为萤火虫数目阀值,|Nk(t)|为领域集内萤火虫数量。

与其他智能算法一样,基本GSO同样存在收敛精度低、容易陷入局部最优的缺陷。本文借鉴混合蛙跳算法(shuffled frog leaping algorithm,SFLA)[10]族群划分思想,将萤火虫群体划分成规模相同的子族群(如图1所示),萤火虫首先在子族群中进行一定次数局部搜索,然后参与整个种群信息交流。局部迭代和全局信息交换提高了GSO收敛效率。萤火虫种群划分子族群方法为:将S只萤火虫f[Xk(t)]降序排列,并均分到Z个族群中,每个萤火虫族群的萤火虫数为Q,设Ei表示第i个族群,有:

Ei(t)={Xr+Q(i-1)(t)∈S|1≤i≤Q}

(9)

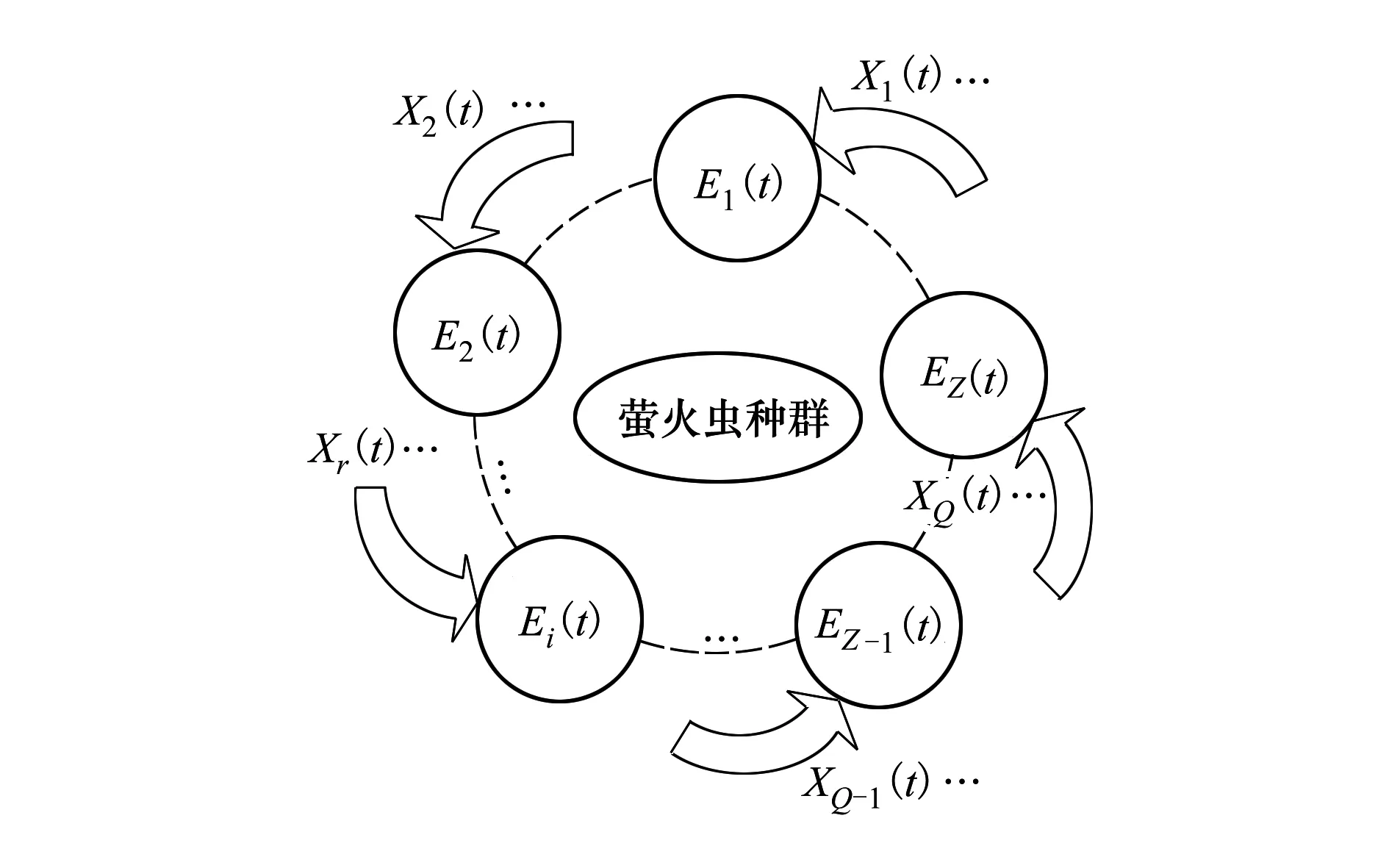
图1 GSO子族群划分机制

2.2 混合蛙跳算法(SFLA)

SFLA也是一种基于群体智能的启发式计算技术,具有粒子群算法及Memetic算法的优点[10]。SFLA工作过程可以描述为:随机生成F只青蛙群体Pt={X1(t),…,Xk(t),…,XF(t)},k=1,2,…,F,第k只青蛙位置Xk(t)={xk1(t),xk2(t),…,xkn(t)}(n为目标函数维数)。按函数适应度值f[Xk(t)]将青蛙降序排列,并均分到M个族群中,每个族群的青蛙数为N。设Ej表示第j个族群,有:

Ej={Xj+M(l-1)(t)∈Pt|1≤l≤N},1≤j≤M

(10)

SFLA对每个族群中函数适应度值最差的解Xw(t)按(11)式更新:

Xnew(t)=Xw(t)+r·[Xb(t)-Xw(t)]

(11)

式中：r∈[0,1]为随机数,Xb(t)为族群中适应度最好的解。如果Xnew(t)位置优于Xw(t),则用Xnew(t)替代Xw(t);否则用青蛙群体中最好的解Xg(t)代替Xb(t)重新执行更新策略(11)式,若Xnew(t)仍然不能优于Xw(t),则随机生成青蛙取代Xw(t)。所有族群重复执行局部搜索过程,直到满足一定的搜索次数为止。

当所有族群完成局部搜索后,更新群体最优解,然后青蛙粒子重新混合,再次划分族群,并执行局部搜索,直到满足终止条件为止。

2.3 具有多智能群体的MIGSO

GSO将荧光素交流限制在领域集空间内,使得萤火虫群体划分成分为若干聚集区域,一定程度上降低了算法陷入局部最优极值的概率,但是具有很强荧光素的萤火虫只能对其领域集内的其他个体产生作用,与其他的萤火虫无法进行交流,导致个体最优信息无法在群体内传递,限制了算法收敛速度。SFLA具有实现容易、运算速度快、寻优能力强等特点,但是对反馈信息利用不足,求解精度相对较低。

为了提高GSO跳出局部极值的能力,本文将GSO与SFLA融合,融合的方法是将种群划分成规模相同的2个种群:GSO群和SFLA群。2个种群独立执行各自的搜索操作,2个种群在每次迭代结束后进行最优信息交流,即当2种算法完成t次全局迭代后,GSO算法得到的最优解为XGSO(t),SFLA得到的最优解为XSFLA(t),比较两者的目标函数值,若f[XGSO(t)]≥f[XSFLA(t)],则用XGSO(t)代替XSFLA(t)来引导青蛙的进化方向,否则用XSFLA(t)代替XGSO(t)来引导萤火虫的进化方向,这样GSO群和SFLA群在进化过程中,充分借鉴了另一群体的最优信息,实现了不同种群协同进化,有效地增强了GSO寻优能力。

2.4 基于MIGSO的协同多目标分配实现

GSO与SFLA算法最初主要应用于连续函数优化问题,由于UCAV协同多目标攻击属于离散问题,因此为了使得MIGSO能够应用于UCAV协同多目标攻击问题中,本文对MIGSO粒子编码方式进行了离散处理,并给出适合离散编码的萤火虫更新策略。

定义5 MIGSO中粒子编码定义为Xk(t)=(xk1,…,xkl,…,xkn)T,其中xkl∈[0,m],Xk(t)∩[0,m]≠ø。

例如:对于编码A=(1,1,2,3,3,3,4,5,5),它表示当m=5,n=9时,目标1、2分配给第1架无人机,目标3分配给第2架无人机,目标4、5、6分配给第3架无人机,目标7分配给第4架无人机,目标8、9分配给第5架无人机。

对于离散型萤火虫编码方式,如果仍然采取(6)式及(11)式进行更新,则会产生大量不符合要求的解,严重降低了算法求解速度,因此本文给出了一种适合离散编码的MIGSO粒子更新策略,具体更新策略如下:

Xk(t+1)=Xk(t)+D

(12)

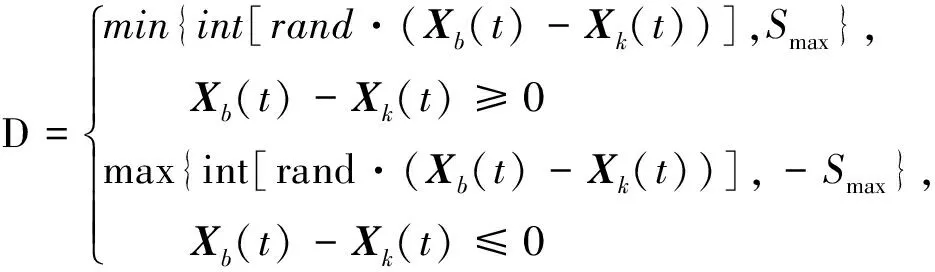
(13)

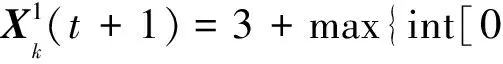
2.5 MIGSO算法流程

MIGSO算法流程可以描述为:

∥初始化

1)t←0,k←0,l←0,i←0;

2) 相关参数和系数设置;

3) 设定最大循环次数Tmax,Tlocal;

4) 随机生成萤火虫初始群体,并均分成GSO群体和SFLA群体;

While (t≤Tmax) do

{

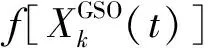
6) 根据(9)式和(10)式分别对2种群进行种群划分;

∥2种群进行局部搜索

While (k≤Tlocal) do

{

While (i≤Q) do

{

7) GSO种群内萤火虫根据(5,8,12,13)式更新;

8)i←i+1

}

While (l≤m) do

{

9) SFLA种群内青蛙根据(12)式、(13)式更新;

10)l←l+1

}

k←k+1

}

∥种群最优信息交换

∥萤火虫全局信息更新

12) 更新全局最优解Xbest(t);

13)t←t+1

}

程序结束,输出全局最优解。

3 仿真分析

3.1 算例仿真

为了验证MIGSO算法有效性,对于算例A:红方无人作战飞机m=5,ri=4,蓝方地面目标n=10。无人机生存概率Wij、杀伤概率Pij、目标价值Qj及无人机价值Vi如表1～4所示,由于攻击目标比较集中,因此设Dij在[15,25]范围内取随机数。

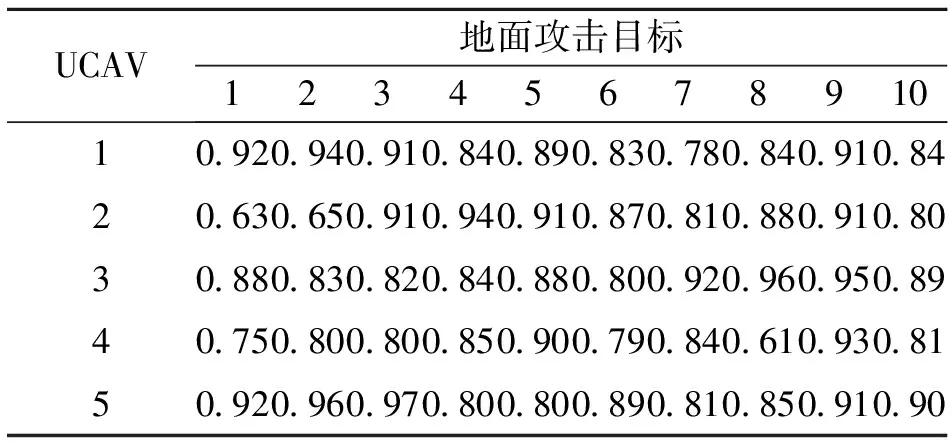
表1 UCAV生存概率Wij

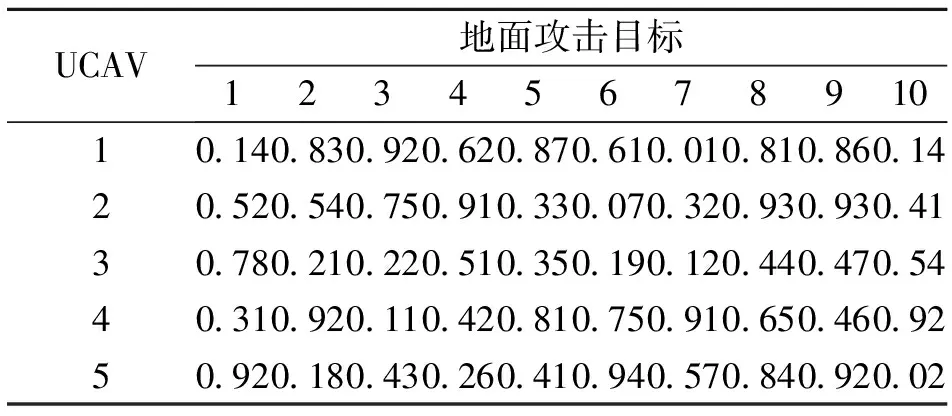
表2 UCAV杀伤概率Pij

表3 目标价值Qj

表4 UCAV价值Vi

MIGSO算法参数设置:S=200,Nt=5,Q=20,l0=5,ρ=0.3,γ=0.6,ω1=0.7,ω2=0.2,ω3=0.1,β=0.08,Smax=3。在Matlab仿真平台中,采用MIGSO算法进行仿真,进行50次试验,最优分配方案如表5所示,图2给出了MIGSO收敛曲线。

表5 目标分配方案

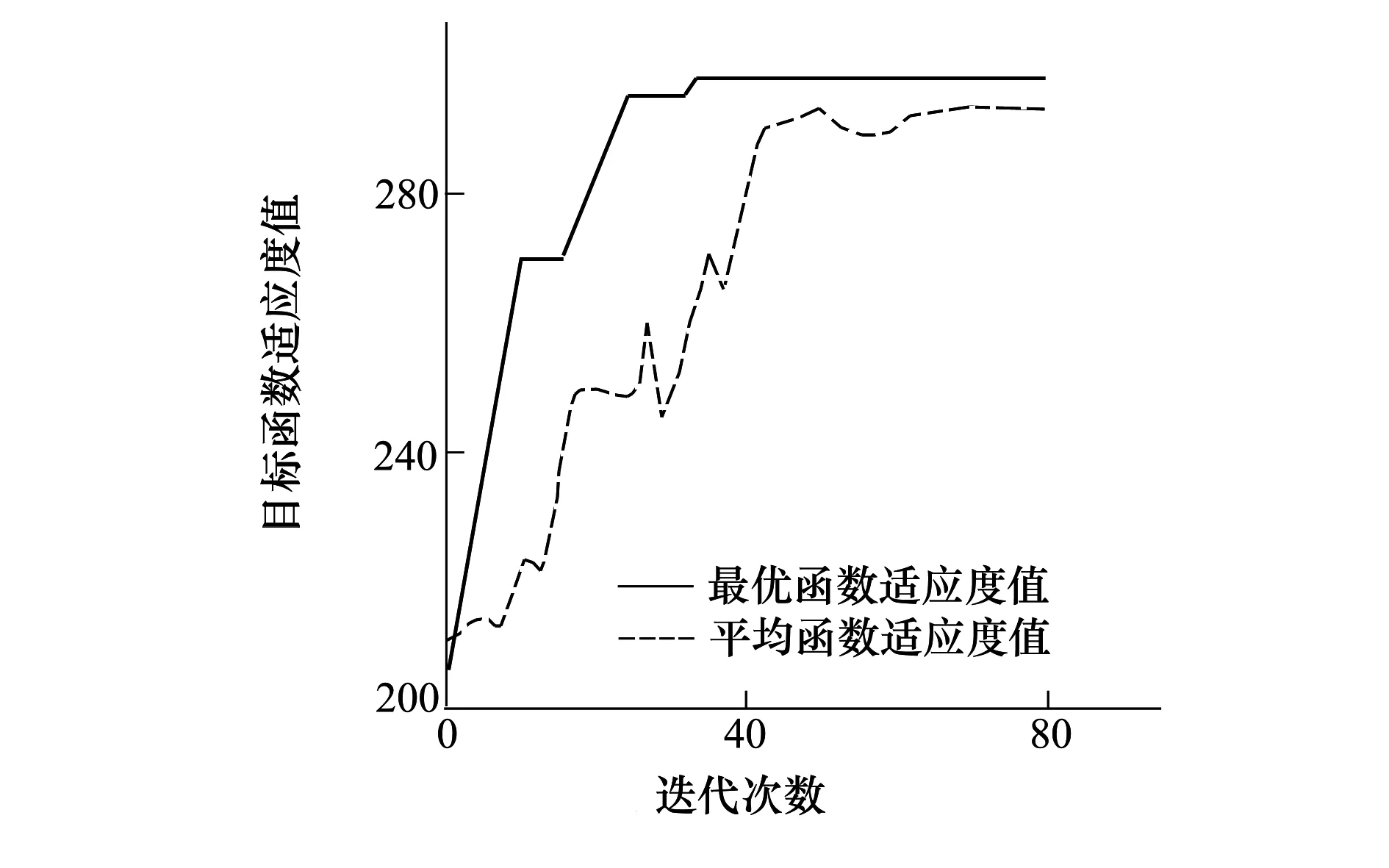
图2 MIGSO收敛曲线

从表5可以看出,由于U3具有较高价值且对目标杀伤概率较低,因此分配了一个目标;对于U4,其具有较强的生存能力且对目标杀伤概率较高,因此分配了3个目标,这种目标分配方案符合作战实际情况。

3.2 MIGSO算法性能分析

为了进一步分析MIGSO算法性能,分别采用GSO和MIGSO算法对算例A进行仿真,分别运行50次。仿真结果如图3所示。

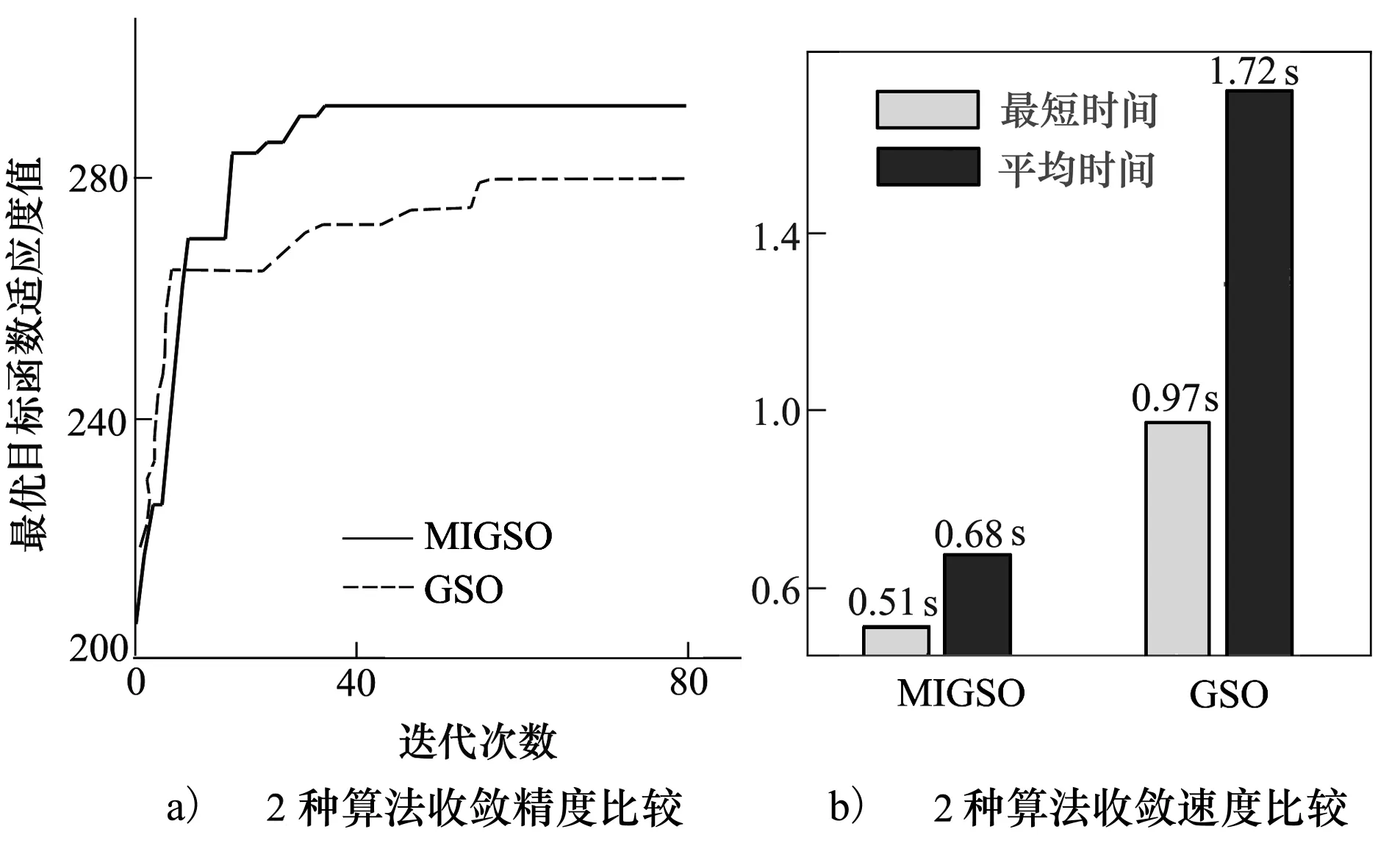
图3 MIGSO与GSO算法性能比较

从图3可以看出,MIGSO无论在求解精度方面还是在运算时间上都要优于GSO算法。仿真结果表明,MIGSO算法之所以能够快速合理地给出UCAV协同多目标分配方案,是因为MIGSO采用特殊的编码方式及萤火虫更新策略,同时局部搜索及全局信息交换的方式有效的改善了算法求解精度,而且MIGSO采用多种群协同进化机制,通过不同种群间最优信息共享,实现了协同进化,进一步提高了算法的收敛效率。

4 结 论

研究了UCAV协同多目标分配问题,针对GSO算法的不足将其与SFLA算法融合,提出了基于多群体改进萤火虫优化(MIGSO)算法的UCAV目标分配算法,建立了基于收益指标、消耗指标及航程指标为准则的数学模型,并将MIGSO应用于UCAV协同多目标分配问题中,给出了算法具体流程与仿真实例。仿真结果表明,MIGSO算法可快速有效地计算出目标分配方案,且分配结果符合作战实际。

参考文献：

[1] 刘万俊，傅裕松，翁兴伟. 有人机-无人机群协同空战目标分配算法[J]. 火力与指挥控制，2012，37(5)：124-127

Liu Wanjun, Fu Yusong, Wong Xingwei. Reseach on Mission Assignment Algorithm of Cooperation Air Combat for MAV and Multi-UAV[J]. Fire Control and Command Control, 2012, 37(5): 124-127 (in Chinese)

[2] 罗贺，胡小建，付超. 多无人机协同目标分配仿真系统设计与实现[J]. 系统仿真学报，2009，21(11)：3246-3250

Luo He, Hu Xiaojian, Fu Chao. Design of Multi-UAVs′Target Allocating Simulation System and Its Implementation[J]. Journal of System Simulation，2009，21(11)：3246-3250 (in Chinese)

[3] 程聪，吴庆宪，刘敏,等. UCAV协同攻击多目标的任务分配技术研究[J]. 吉林大学学报:信息科学版，2012，30(6)：609-615

Ren Cong, Wu Qingxian, Liu Min, et al. Research on Task Allocation for UCAVs Cooperatively Attacking Multiple Targets[J]. Journal of Jilin University: Information Science Edition, 2012，30(6)：609-615 (in Chinese)

[4] Griggs B J, Parnell G S. An Air Mission Planning Algorithm Using Decision Analysis and Mixed Integer Programming[J]. Operations Research, 1997, 45(5): 662-676

[5] 唐传林，杜海文，吴文超,等. 基于博弈论的多UCAV对地攻击目标分配[J]. 电光与控制，2011，18(10)：28-31

Tang Chuanlin, Du Haiwen, Wu Wenchao, et al. Game Theory Based Target Assignment for Multiple UCAVs in Air to Ground Attack[J]. Electronics Optics and Control, 2011, 18(10): 28-31 (in Chinese)

[6] 杨尚君，王社伟，陶军,等. 动态环境下的多UCAV 协同任务分配研究[J]. 电光与控制，2012，19(7)：32-36

Yang Shangjun, Wang Shewei, Tao Jun, et al. Multi-UCAV Cooperative Task Allocation in Dynamic Environment[J]. Electronics Optics and Control，2012，19(7)：32-36 (in Chinese)

[7] Krishnanand K N，Ghose D. Theoretical Foundations for Rendezvous of Glowworm-Inspired Agent Swarms at Multiple Locations[J]. Robotics and Autonomous Systems，2008，56(7)：549-569

[8] Huang Zhengxin, Zhou Yongquan. Using Glowworm Swarm Optimization Algorithm for Clustering Analysis[J]. Journal of Convergence Information Technology, 2011, 6(2): 78-85

[9] 叶文，朱爱红，潘长鹏. 多UCAV协同目标分配算法研究[J]. 系统工程与电子技术，2010，32(1)：104-108

Ye Wen, Zhu Aihong, Pan Changpeng. Cooperation Mission Assignment Algorithm for Multi-UCAV[J]. Systems Engineering and Electronics, 2010，32(1)：104-108 (in Chinese)

[10] Deep K, Bansal J C. Mean Particle Swarm Optimization for Function Optimization. International Journal of Computational Intelligence Studies, 2009, 1(1) : 72-92