基于在线RBF神经网络的BTT导弹控制器设计

方群, 王祥

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学国家重点实验室, 陕西 西安 710072)

BTT导弹控制技术能显著提高导弹的机动性、稳定性、升阻比特性,是目前导弹控制系统设计领域的一个重要研究方向。为了实现BTT控制,导弹必须快速滚动到理想的机动方向,且需限制导弹的偏航运动,BTT导弹的这种控制方式使其成为一个具有运动学耦合、惯性耦合的时变非线性多变量控制系统。

反馈线性化是导弹非线性飞行控制系统设计中一个常见方法,采用反馈线性化方法可以实现非线性对象的线性化和通道之间的解耦控制。反馈线性化方法的缺点在于对系统模型的误差十分敏感,为此国内外学者展开了广泛的研究。其中一个重要研究方向就是基于智能控制算法在线补偿飞行控制系统动态逆误差,以此增加系统的鲁棒控制性能。张友安等[1]将FCMAC神经网络运用到BTT导弹的自动驾驶仪的设计,使具有不确定性的设计系统获得要求的跟踪特性;杨志峰等[2]基于模糊控制系统设计方法,提出了一种自适应鲁棒控制律,对导弹飞行控制系统动态逆误差的在线补偿,实现了BTT导弹飞行控制系统的高精度鲁棒控制;宋申民等[3]针对具有不确定性的BTT导弹控制系统,采用自适应神经网络方法设计了控制器;朱凯等[4]针对非匹配不确定性的BTT导弹非线性动力学模型, 结合反演控制、自适应控制和滑模控制方法,设计了自适应滑模反演控制器; 张颖昕等[5]针对BTT导弹大迎角和快速滚动状态的非线性问题,提出了一种基于分散控制思想的协调式鲁棒H∞控制器设计方法。

本文基于非线性反馈线性化理论,针对反馈线性化控制器对系统不确定性的鲁棒性差的问题,引入在线RBF神经网络,设计了基于反馈线性化控制的自适应BTT导弹飞行控制器。通过数值仿真,对所提出控制器的有效性进行了验证。

1 基于时标分离的双回路飞行控制系统数学模型

导弹在飞行控制过程中,气动力改变导致力矩改变时,首先会引起导弹快回路姿态角速度的变化,然后导弹的慢回路姿态角发生改变。这种飞行控制系统状态的时标分离特性,可以应用多重尺度奇异摄动理论,将飞行控制系统分成2个快慢变化不同的双回路控制系统结构。基于时标分离假设,参考Have Dash II BTT 空空导弹非线性动力学方程[2],可得形如(1)式的双回路控制系统数学模型

(1)

式中：x1表示导弹姿态角(α,β,φ),x2表示导弹的姿态角速度(p,q,r),控制量u为气动舵偏(δe,δa,δr),f1、f2、g1、g2的具体表达式可以参见文献[2]。

2 基于RBF神经网络的自适应反馈线性化控制系统

对于BTT导弹飞行控制系统的设计问题,考虑如下非线性系统

(2)

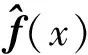
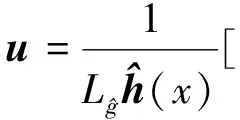
(3)

式中:υc为虚拟控制量。将(3)式作为控制量和实际非线性系统(2)式的输入,则可以得到系统的输出动态

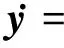
(4)

实际上,系统动态逆误差是由系统模型误差、求逆计算误差和外界干扰等引起。对于基于反馈线性化控制的飞行控制系统,逆误差的存在将使得飞行控制系统鲁棒性能变差,甚至使控制系统失效。为了消除动态逆误差对反馈线性化控制系统的影响,本文采用基于RBF神经网络的自适应控制器对动态逆误差进行补偿。

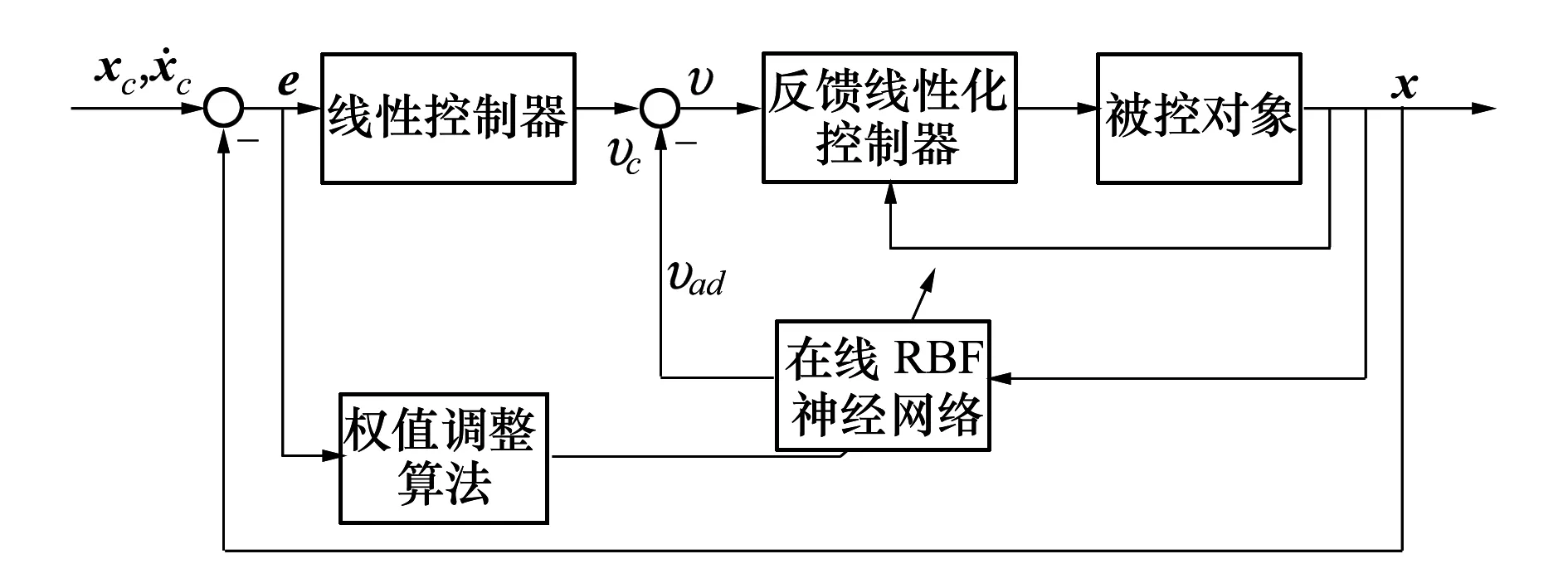
图1 基于RBF神经网络的自适应控制系统结构图

构造基于RBF神经网络的自适应反馈线性化控制系统,其结构如图1所示。由系统结构图可知,伪控制量由两部分组成

υ=υc-υad

(5)

式中：υad为RBF神经网络输出的自适应补偿信号,υc为线性控制器的输出

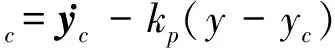
(6)

将(3)式中虚拟控制量替换为υ,则可得基于RBF神经网络的自适应反馈线性化控制器

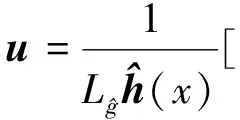
(7)

定义系统(2)式的输出误差向量e=y-yc,并将(7)式代入,则有

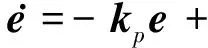
(8)

可见,当神经网络输出υad可以完全补偿动态逆误差Δ时,系统输出误差将会逐渐趋于零,从而能够保证稳定跟踪期望的输出信号。

3 在线自适应RBF神经网络逼近原理

RBF神经网络是由输入层、一个隐含层和线性输出层组成,输入层到隐含层的映射关系为非线性的高斯基函数,隐含层到输出层的映射关系为简单的线性映射,可用如下数学模型描述

y=WTφ(X)

式中：X∈Rn,为神经网络输入向量;y∈Rm,为神经网络输出向量;W∈Rl×m,为权值矩阵;φ(·)∈Rl,为隐含层输出向量。其中,φi(X)为高斯基函数,具体表达式为

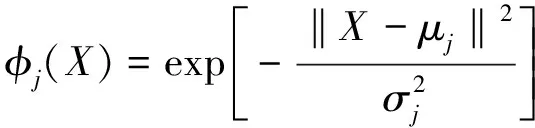
Δ=W*Tφ*(X)+ε,‖ε‖≤εΠ

(9)

υad=WTφ(X)+ν

(10)

式中：ν为鲁棒自适应项,选取RBF神经网络参数的在线调整规则为

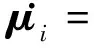
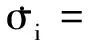
(11)

式中：Γw、Γμ、Γσ和δw、δμ、δσ为设计参数,且Γw、Γμ、Γσ均为正定对称矩阵。

4 基于RBF神经网络的自适应反馈线性化飞行控制系统设计

针对BTT导弹飞行控制系统,本文提出了一种基于RBF神经网络的自适应反馈线性化飞行控制系统， 如图2所示。

图2 基于RBF神经网络的反馈线性化飞行控制系统框图

基于第2节自适应反馈线性化控制器设计方法,对角速度层控制律进行设计,则有

(12)

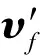
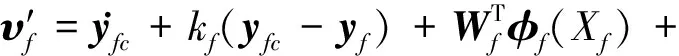
(13)

鲁棒控制项νf为

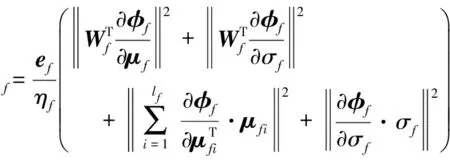
(14)

式中:Xf=ef为角速度层RBF神经网络的输入样本,lf为神经网络的隐层节点数。选择神经网络结构参数的自适应调节规律为

各地应将乡村旅游项目建设用地纳入国土空间规划和年度土地利用计划统筹安排。在符合生态环境保护要求和相关规划的前提下，鼓励各地按照相关规定，盘活农村闲置建设用地资源，开展城乡建设用地增减挂钩，优化建设用地结构和布局，促进休闲农业和乡村旅游发展，提高土地节约集约利用水平。鼓励通过流转等方式取得属于文物建筑的农民房屋及宅基地使用权，统一保护开发利用。在充分保障农民宅基地用益物权的前提下，探索农村集体经济组织以出租、入股、合作等方式盘活利用闲置宅基地和农房，按照规划要求和用地标准，改造建设乡村旅游接待和活动场所。支持历史遗留工矿废弃地再利用、荒滩等未利用土地开发乡村旅游。

(15)

对姿态层带动态逆误差补偿的控制器有

(16)

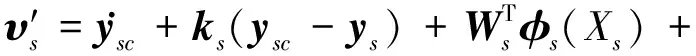
(17)

鲁棒控制项νs为

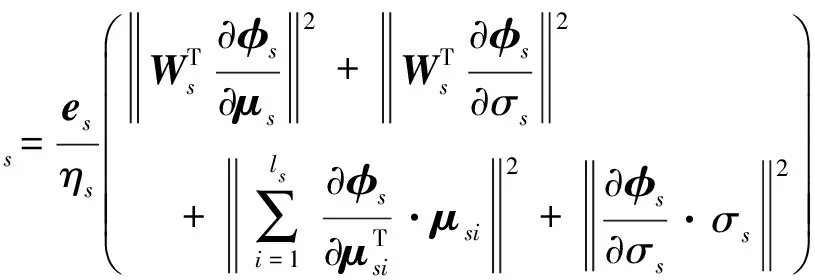
(18)

式中：Xs=es为姿态层RBF神经网络的输入样本,ls为神经网络的隐层节点数。选择神经网络结构参数的自适应调节规律为

(19)

5 仿真与分析

为了验证本文提出的飞行控制系统设计方案的有效性,基于文献[6]提供的气动数据,通过数值仿真对所提出控制器的在线自适应能力和对控制系统模型的不确定性及外界干扰的鲁棒性进行验证。

导弹初始高度为7 km,初始速度为1 000 m/s,初始姿态角和姿态角速度均为0,攻角α0为零,侧滑角β0为5°。

仿真算例中,飞行控制系统模型在0～3 s为标称系统;在3～6 s,气动参数上浮20%;在6～9 s,引入垂直阵风的影响。

考虑外界干扰阵风的飞行控制系统模型变为

(20)

根据BTT导弹飞行控制系统快慢回路的响应特性,可选取自适应飞行控制器的设计参数为:kf=diag(20,20,20),ks=diag(5,5,5),ηf=ηs=1,Γfw=I,Γfμ=10I,Γsw=I,Γsμ=2I,Γfσ=Γsσ=1,δfw=δfμ=δfσ=1,δsw=δsμ=δsσ=0.01。

仿真结果见图3～图5。图中,直线表示采用反馈线性化控制器设计方案,虚线表示本文提出的在线自适应飞行控制器设计方案,点划线表示参考输入。

数值仿真结果表明,对于本文所设计的自适应飞行控制器(15)式和(18)式,权值初始值量级对所设计控制器的收敛特性和控制性能具有一定的影响,W量级为10-3,μ量级为101,σ量级为102。

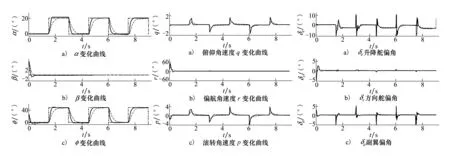
图3 姿态角变化曲线 图4 角速度变化曲线 图5 舵偏角指令曲线

由图3～图5可以看出,采用基于RBF神经网络的自适应反馈线性化控制系统,能够快速、精确地跟踪姿态角输入指令。同仅采用反馈线性化控制的飞行控制器设计方案相比,基于RBF神经网络的自适应反馈线性化控制系统,对气动参数扰动具有较好的自适应能力。当气动扰动存在不确定性时,仍能实现对期望的指令角度的快速、精确的跟踪,且姿态角转动速率和舵偏角能够满足导弹系统性能的要求。

6 结 论

本文针对BTT导弹飞行控制系统的自适应鲁棒控制问题,基于反馈线性化控制理论和在线自适应RBF神经网络控制系统设计方法,设计了自适应反馈线性化飞行控制器。所设计的飞行控制器,通过反馈线性化控制理论实现对控制系统的解耦控制,基于RBF神经网络对系统动态逆误差进行在线逼近,实现对BTT导弹飞行控制系统不确定性和外界扰动的补偿,有效解决了BTT飞行控制系统通道耦合和数学模型不精确带来的控制器设计问题。通过数值仿真,对反馈线性化飞行控制器和本文提出的在线自适应飞行控制器进行了仿真比较分析。仿真结果表明,本文所提出的飞行控制系统设计方法,能有效克服反馈线性化飞行控制器对模型不确定性鲁棒性差的缺点, 从而实现对不确定飞行控制系统的实时、精确和鲁棒控制。

参考文献：

[1] 张友安,杨华东,顾文锦,等. 空空导弹控制系统鲁棒动态逆设计[J]. 系统工程与电子技术, 2004, 8(26):1084-1089

Zhang Youan, Yang Huadong, Gu Wenjin, et al. Robust Dynamic Inversion Controller Design for Air-to-Air Missiles[J]. Systems Engineering and Electronics, 2004, 8(26):1084-1089 (in Chinese)

[2] 杨志峰,雷虎民,李庆良,等. 基于RBF神经网络的导弹鲁棒动态逆控制[J]. 宇航学报, 2010, 31(10): 2293-2300

Yang Zhifeng, Lei Humin, Li Qingliang, et al. RBF Neural-Network-Based Robust Dynamic Inverse Control for a Missile[J]. Journal of Astronautics, 2010, 31(10): 2293-2300 (in Chinese)

[3] 宋申民,于志刚,段广仁. BTT导弹自适应神经网络控制[J]. 宇航学报, 2007, 28 (5): 1224-1230

Song Shenmin, Yu Zhigang, Duan Guangren. Adaptive Neural Network Control for BTT Missile[J]. Journal of Astronautics, 2007, 28 (5): 1224-1230 (in Chinese)

[4] 朱凯, 齐乃明, 秦昌茂. BTT导弹的自适应滑模反演控制设计[J]. 宇航学报, 2012, 31(3): 769-773

Zhu Kai, Qi Naiming, Qin Maochang. Adaptive Sliding Mode Controller Design for BTT Missile Based on Backstepping Control[J]. Journal of Astronautics, 2012, 31(3): 769-773 (in Chinese)

[5] 张颖昕, 董朝阳, 王青, 陈宇. BTT导弹的协调式分散鲁棒H∞控制器设计[J].宇航学报, 2011, 32 (4): 734-740

Zhang Yingxin, Dong Chaoyang, Wang Qing, Chen Yu. Decentralized RobustH∞Controller Design for Bank-to-Turn Missile with Coordinate Loop[J]. Journal of Astronautics, 2011, 32 (4): 734-740 (in Chinese)

[6] Wang Q, Stengel R.F. Robust Nonlinear Flight Control of a High Performance Aircraft[J]. IEEE Trans on Control Systems Technology, 2005, 13(1): 15-26

[7] Michael B M. Adaptive Nonlinear Control of Missile Using Neural Networks [D]. Atlanta: Georgia Institute of Technology, 1997

[8] 张友安,胡云安. 导弹控制和制导系统的非线性设计方法[M]. 北京:国防工业出版社, 2003

Zhang Youan, Hu Yunan. Nonlinear Design Approaches for Missile Control and Guidance[M]. Beijing: National Defence Industry Press, 2003 (in Chinese)

[9] Uang Hueyjian, Chen Borsen. Robust Adaptive Optimal Tracking Design for Uncertain Missile Systems: a Fuzzy Approach[J]. Fuzzy Sects and Systems, 2002, 126: 63-87