降低气动舵操纵耦合的高超声速飞行器总体优化研究

周敏, 周军, 林鹏

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

高超声速飞行器各通道间的强非线性耦合导致传统的多通道解耦设计方法不再适用，给控制学科带来新挑战[1]。目前，针对高超声速飞行器强耦合特性下的控制方法研究取得一定进展，其中以状态空间解耦法的研究最为深入，但由于对模型精确性及相关矩阵可逆性的苛刻要求，该方法的应用受到限制[2]。而工程实际中将耦合作为随机干扰，利用系统稳定裕度克服其影响的方法不能真实反映耦合特性的作用大小、作用方向和作用机理，具有一定的盲目性和不确定性，往往会产生意想不到的甚至灾难性的后果[1]。因此，改善高超声速飞行器的通道间交叉耦合特性对于其控制系统的设计具有重要意义。与随控布局飞机充分发挥控制系统潜能从而可以放宽总体要求的设计思想相反，本文基于推广的总体随控布局思想[3-4]，从降低控制系统设计难度的角度出发对高超声速飞行器总体提出了通道间耦合小的优化设计要求。重点研究气动舵控制的高超声速飞行器通道间操纵耦合特性，引入操纵耦合度定义作为高超声速飞行器通道间操纵耦合特性的评价指标；通过建立操纵耦合度与飞行器总体参数的表征模型，为高超声速飞行器总体随控优化提供目标函数；确定了以降低气动舵操纵耦合为目标的高超声速飞行器总体随控优化方法，有效降低了气动舵控制高超声速飞行器通道间的操纵耦合作用。

1 气动舵操纵耦合特性

高超声速飞行器的总体随控优化是从控制学科角度提出的，而控制性能主要体现在飞行器短周期运动中，与其受到的力矩作用密切相关[3]，因此，本文围绕高超声速飞行器所受气动力矩的耦合特性开展总体随控优化研究。

本文研究对象为翼身组合高速飞行器，外形如图1所示[3]。忽略次要因素，建立气动力矩系数表征形式为

(1)

图1 基准外形及总体参数

2 气动舵操纵耦合特性评价指标定义

气动舵控制高超声速飞行器的操纵耦合特性评价指标应满足：①能合理描述本通道受其他通道气动舵面偏转耦合影响大小；②能真实反映飞行器操纵耦合特性，与飞控系统控制指令无直接关联。因此，定义操纵耦合特性评价指标——操纵耦合度为

1)差动舵δx偏转下的操纵耦合度

(2)

2)方向舵δy偏转下的操纵耦合度

(3)

3 操纵耦合度与总体参数关系

确定高超声速飞行器操纵耦合度与总体外形参数之间的函数关系是进行总体随控优化的前提。本文采用工程估算与CFD相结合的方法，建立操纵耦合度与总体参数的表征关系模型。

3.1 工程估算建立耦合度模型

(4)

式中：Scwr、Scw分别为方向舵和垂尾面积，ycwr为方向舵面心到弹体纵轴的距离。

(5)

(6)

3.2 CFD方法建立耦合度模型

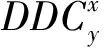
(7)

(8)

(9)

4 总体随控优化策略

基于广义随控布局思想[3]，以建立的操纵耦合度模型(6)式～(9)式为目标函数，以影响气动舵操纵耦合度大小的飞行器总体参数为决策变量，开展高超声速飞行器总体随控优化，流程如图2所示包括4个具体步骤。

步骤1 确定总体随控优化目标函数

减小操纵耦合度可改善如图1所示气动舵控制高超声速飞行器的操纵耦合特性，确定高超声速飞行器总体随控优化目标函数为

(10)

步骤2 确定决策变量X及寻优边界

高超声速飞行器操纵耦合度模型表明,影响操纵耦合特性的总体参数有:头部椎段长度Lz、圆柱段长度Lc、收缩尾部长度Lt、弹体直径D、垂尾展长l-cw、垂尾梢弦b1-cw、外露垂尾根弦bs-cw、方向舵展长lr-cw、方向舵弦长br-cw、弹翼根弦中点距离头部顶点距离Lw、毛机翼根弦bs-w、弹翼梢弦b1-w、弹翼翼展l-w、升降舵展长lr-w、升降舵弦长br-w,因此,确定总体随控优化的决策变量X为

步骤3 确定总体随控优化约束条件

总体随控优化约束条件应满足以下2点要求:

1) 保证飞行器锥柱裙弹身-单后掠梯形翼-单垂尾的基本外形特点不变,确定约束条件如下所示:

2Lw+bs-w-2Lz-2Lc≤0

bl-cw-bs-cw≤0

D-l-cw≤0

2lr-cw-(lcw-D)≤0

bl-w-bs-w≤0

D-l-w≤0

(11)

2) 保证影响壳体相对质量、有效载荷、弹载仪器和动力装置排布方案、机体强度等因素的特征参数变化小,引入约束条件

(1-k)Γ-0≤Γ≤(1+k)Γ-0

Γ[λB,λn,λt,λ-cw,η-cw,λ-w,η-w]

(12)

式中:λB、λn、λt分别为弹身、头部和尾部长径比;λ-cw、η-cw分别为垂尾展弦比和根梢比;λ-w、η-w分别为毛机翼展弦比和根梢比;下标“-0”表示各特征参数的初始值;k表示基准外形特征参数可容忍的变化范围。将(11)式、(12)式引入的随控优化约束条件统一记为

G(X)≤0

(13)

步骤4 采用多目标粒子群算法寻优,确定优化策略。

降低气动舵操纵耦合的高超声速飞行器总体随控优化模型为

采用多目标粒子群算法寻优,得到多组可行解,选择可行解XOP为总体随控优化策略。

图2 总体随控优化流程

5 算例分析

引入如图1所示外形的算例高超声速飞行器,根据以上优化步骤对其进行总体随控优化。在基准外形参数X-0下算例飞行器的操纵耦合度分别为

采用多目标粒子群方法寻优,设定以下参数:

1)设定决策变量寻优边界为以初始值X-0为中心的50%邻域;

2)设定飞行器特征参数可容忍10%的较小调整,即约束条件式(12)中k=10%。

得到一组可行解为

此时,各操纵耦合度为

显然，以此可行解作为飞行器总体随控优化策略可有效降低操纵耦合。

采用工程中最常用的PID控制方法对算例飞行器优化效果进行仿真验证，思路如图3所示。仿真曲线如图4所示，算例飞行器优化后各通道跟踪曲线与解耦系统曲线基本重合；基于解耦系统设计的控制器在未优化系统下的控制性能无法保证，如仿真结果所示偏航通道的控制性能严重下降。仿真结果表明，降低高超声速飞行器操纵耦合特性对于控制系统设计具有重要意义。

图3 总体随控优化策略验证思路

图4 优化前后系统跟踪曲线

6 结 论

本文针对气动舵控制高超声速飞行器的操纵强耦合特性给控制系统设计带来的问题，基于广义随控布局思想，从简化控制系统工程设计的角度出发给总体提出了通道间操纵耦合小的优化设计要求。通过研究对象飞行器气动力矩组成特点，引入飞行器操纵耦合特性度量指标——操纵耦合度的定义。结合工程估算与CFD方法建立了操纵耦合度与飞行器总体参数的表征关系，以该函数最小作为飞行器总体随控优化目标；采用多目标粒子群优化算法寻优，得到可降低高超声速飞行器操纵耦合特性的总体随控优化策略。最后，采用工程中常用的PID控制方法对算例飞行器的总体随控优化策略进行了检验，结果表明本文提出的总体随控优化方法对于存在严重操纵耦合作用的高超声速飞行器控制系统设计具有重要意义。

参考文献：

[1] 黄琳，段志生，杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用，2011，28(10)：1496-1505

Huang Lin, Duan Zhisheng, Yang Jianying. Challenge of Control Science in Near Space Hypersonic Aircrafts[J]. Control Theory & Applications，2011，28(10)：1496-1505 (in Chinese)

[2] Antony Snell. Decoupling Control Design with Applications to Flight[J]. Journal of Guidance, Control and Dynamics, 1998，21(4)：647-655

[3] 周军，周敏，林鹏. 降低气动非线性的高超飞行器总体优化方法研究[J]. 宇航学报，2012，33(7)：871-875

Zhou Jun, Zhou Min, Lin Peng. Research on the Control-Configured Optimization to Reduce Aerodynamic Nonlinearity of Hypersonic Vehicles[J]. Journal of Astronautics, 2012, 33(7)：871-875 (in Chinese)

[4] Anderson M R, Mason W H. An MDO Approach to Control-Configured-Vehicle Design[C]∥Symposium on Multidisciplinary Analysis and Optimization. 1996, 734-743

[5] 苗瑞生,居贤铭,吴甲生. 导弹空气动力学[M]. 北京：国防工业出版社, 2006：509-519

Miao Ruisheng, Ju Xianming, Wu Jiasheng. Missile Aerodynamics[M]. Beijing: National Defense Industry Press, 2006：509-519 (in Chinese)