基于平流层特殊风场的浮空器定点方案研究

常晓飞, 白云飞, 符文星, 闫杰

(西北工业大学 航天学院, 陕西 西安 710072)

平流层浮空器是指在20～35 km平流层内飞行的浮空器,通过携带不同的有效载荷,完成数据通讯、地面观测、战场监控等任务,具有滞空时间长、覆盖面积广、生存能力强、观测分辨率高、成本较低等优点[1]。为了实现浮空器在某一区域上空的定点驻留或机动飞行,传统平流层飞艇方案采用螺旋桨为动力,为克服平流层水平风对定点飞行的影响,要求螺旋桨始终工作,能耗问题成为制约其有控飞行的瓶颈因素[2]。

本文基于平流层底部存在准零风层这一特殊的风场特性,借鉴美国Global Aerospace公司的平流层卫星系统,提出了一种全新的浮空器定点部署方案。论文介绍了系统构成和定点控制原理,并通过建模仿真验证了方案可行性。

1 平流层底部的准零风层

在平流层高度,大气运动以东西方向的水平运动为主,垂直对流相对较弱。

1975年,Belmont等[3]通过对平流层风场进行研究发现,平流层在冬夏转换期间东西风向发生翻转,在东风区和西风区之间存在空间范围较大、时间上比较稳定的纬向风转换层。2002年,吕达仁等[4]提出了准零风层(quasi-zero wind layer,QZWL)的概念,是指在平流层底部20 km高度附近的大气层中,上下层纬向风风向相反。在准零风层下部为著名的西风带,随着高度的上升,风速会逐渐减小,到达一定高度后,风速减为零,随着高度的继续增加,风向变为东风;在准零风层的高度内,南北方向风速维持在较小的量级。肖存英等[5]和陶梦初等[6]利用ECMWF提供的ERA-40再分析风场资料分析了准零风层的特点及其变化特征。Morris等[7]研究了南纬地区准零风层的分布情况。

本文针对中央气象局提供的多地十年间高空等压面风场气象数据进行了大量统计分析,明确了平流层底部这一特殊的风场特性,并建立了部分地区的准零风层附近的风场模型。图1为我国某地区准零风层附近风随高度变化曲线,可以看出在20 km左右的高空存在明显的准零风层,下层的西南风突变为上层的东北风。图2给出了我国东南部分地区的准零风层高度的统计结果，可以看出，准零风层高度随季节和地域的不同在20 km高度处变化。

图1 东南某地准零风层附近风场变化

图2 东南部分地区准零层高度统计

2 系统组成及定点控制原理

1999年美国Global Aerospace公司提出了平流层卫星系统的概念,在传统高空气球的基础上,采用轨迹控制器实现其经向轨迹控制,使其在平流层内沿东西轨迹绕地球运动[8]。本文借鉴该方案的控制思想,通过修改轨迹控制器结构和控制策略,借助准零风层上下纬向风反向的特点,实现了特定区域的定点驻留和机动飞行。

2.1 系统组成

定点浮空气球系统主要由气球系统、有效载荷吊舱、系绳、轨迹控制器、能源系统、数传系统、定点控制系统、遥测系统和环境保障系统等构成。

图3 平流层可定点气球总体结构

其连接关系如图3所示,从上到下依次为气球、有效载荷吊舱、系绳和轨迹控制器。其中,轨迹控制器主要由机体、垂直翼面、全动水平翼面、垂直舵面和水平舵面组成。

本系统中,浮空气球飞行在平流层底部的准零风层高度附近。系绳用于传递轨迹控制器的控制作用。轨迹控制器位于气球下方6～8 km的西风激流区中,所在高度存在较大的风速和空气密度,其表面动压较大,因此,较小的侧滑角和水平翼面迎角即可产生较好的控制效果。

2.2 定点控制原理

根据风场变化特性将控制系统分为纬向和经向2个通道,其定点控制原理如下:

1) 纬向控制原理

定点浮空气球在东西方向的控制是利用平流层底部存在纬向风向翻转特点来实现。浮空气球工作在准零风层高度附近,通过控制轨迹控制器的全动水平翼面偏角,改变其产生的升力大小和方向,从而改变系绳传递到气球球体的垂直方向的拉力大小,控制气球上升或下降。以此方式控制气球进入到准零风层上面的东风区或下面的西风区,实现气球在东西方向的定点和机动要求。例如,当要求气球向东机动时,减小轨迹控制器产生的升力大小,控制气球高度下降到西风区中,使得其随西风向东飞行。

2) 经向控制原理

通过对气象数据的统计分析可知,准零风高度附近的经向风速常年处于一个较小的量级,因此,经向定点控制可以通过轨迹控制器直接实现。通过控制垂直舵面的偏转来调节轨迹控制器相对气流的侧滑角,继而产生所需要的南北方向控制力,通过系绳拖动气球飞行,消除气球在经向的位置偏差。

3 绳系浮空气球的数学建模

定点浮空气球系统通过系绳将气球和轨迹控制器连接起来,三者的运动相互作用和约束,构成了一个多体系统[9]。

通过对整个系统的运动过程分析可知,浮空气球提供整个系统的静浮力,产生主要的气动力和重力。参考拖船拖曳缆索和飞机拖靶缆绳系统的动力学分析[10-11],认为系统中气球的运动为主要因素,系绳和轨迹控制器处于瞬时平衡状态。即整个系统的运动位置和运动速度是由气球运动决定,系绳的形状和位置由气球运动的拖曳运动形成,轨迹控制器的运动及位置由系绳的末端决定。

3.1 浮空气球数学模型

气球在飞行过程中受到重力、浮力、附加惯性力、气动力和系绳的拉力等作用。

1) 浮力计算

气球受到的浮力计算公式为:

B=VBρag

(1)

式中:VB为气球体积,ρa为空气密度;

2) 重力计算

浮空气球受到的重力包括氦气、气球囊体和有效载荷,计算公式为:

G=(mHe+mB+mLoad)g

(2)

3) 气动力计算

气动力在地面坐标系的三个分量为:

(3)

式中：CBx、CBy、CBz分别为气球在3个方向的气动力系数;Va.x、Va.y、Va.z为气球对空速度在地面坐标系的3个分量,对空速度可由对地速度与风速相加得到;负号表示气球受到的气动力与其运动速度相反。

4) 附加惯性力计算

浮空气球在空气中做非定常运动时,会带动周围的部分空气做加速运动,周围的空气对气球产生反作用,即附加惯性力,其大小与气球运动的加速度成比例,方向与加速度方向相反,该比例常数称为附加质量。在此,认为气球形状为球形,其附加质量可直接从其绕流场的速度势求得:

(4)

式中：R为球体半径。

由于忽略了气球的姿态变化,则气球受到的附加惯性力计算公式为:

(5)

式中:Vk.x、Vk.y、Vk.z分别为气球相对于地面坐标系的速度分量。

5) 系绳拉力计算

浮空气球所受的系绳拉力大小TB、系绳倾角η和系绳偏角ζ可通过系绳模型递推得出。

(6)

6) 质心动力学方程

综上所述,得到气球在地面坐标系的质心动力学方程:

(7)

7) 质心运动学方程

气球的质心运动学方程为:

(8)

3.2 轨迹控制器的平衡方程

根据前面假设,轨迹控制器始终处于力矩平衡状态和力平衡状态;同时,将轨迹控制器作为系绳的一个节点来考虑,其空间位置由系绳形状确定。

1) 力学平衡方程

根据瞬时平衡假设,轨迹控制器受重力、系绳拉力和气动力的作用,3个力的合力为零。其中,轨迹控制器的气动力根据攻角、侧滑角、高度和风速大小等参数求得,然后根据风向与机体的夹角φ将其投影到地面。在地面坐标系中列出平衡方程:

(9)

式中：XC、YC、ZC、GC分别为轨迹控制器受到的阻力、升力、侧向力和重务。

2) 力矩平衡方程

轨迹控制器的力矩平衡方程为:

(10)

根据力矩平衡方程可求出轨迹控制器的平衡攻角和侧滑角,然后计算得到气动力大小,将其代入到力学平衡方程,可以求出轨迹控制器对系绳产生的拉力大小。

3.3 系绳建模

本系统中,系绳不仅受到空气动力和重力的作用,还受到浮空气球和轨迹控制器对其产生的拉力,其建模是本文的难点。参考船用拖缆和系留航空器中对拖缆或系绳的分析[11-12],结合系统特点,本文提出采用“质量集中-轻质刚杆”法进行系绳建模。

本方法假设系绳由多个轻质刚杆及相邻的质量节点构成,每段轻质刚杆没有重量,只受到空气动力的作用,其质量集中到刚杆一端的节点上,而作用在轻质刚杆上的气动力集中作用在该段靠上的节点上。根据“瞬时平衡”假设,设定整个系绳处于力学平衡状态,认为轨迹控制器和气球的系绳系留点是系绳的起点和终点。

在每步仿真运算里,通过计算轨迹控制器的平衡方程可以求得起始节点的系绳拉力、系绳倾角和系绳偏角,将这些条件和轨迹控制器的高度作为初始计算条件,进行迭代计算。根据前一节点的高度、系绳倾角,系绳偏角、以及每段轻质刚杆的长度,可以计算出当前节点在系绳形状坐标系中位置和高度;求解出该节点所处高度的风速大小和方向,以及大气密度和重力加速度;然后计算出该节点处受到的气动力、重力等;根据相邻节点之间的力学平衡关系,求解出当前节点的系绳拉力大小和方向。如此迭代循环,便可以计算出整个系绳所有节点的位置、形状和拉力。

该模型考虑了系绳的重力和空气动力,能够反映通过系绳传递的控制力变化,以及系绳自身形状变化,并能够较方便地转换为计算机仿真模型,详细内容可参考文献[12]。

4 控制系统总体方案

根据飞行任务需求,确定定点浮空气球的总体控制方案如图4所示:

图4 定点浮空气球控制系统总体方案

其纬向和经向控制通道如图5所示。

图5 定点控制系统结构框图

5 全系统动态仿真

下面进行仿真验证。假设仿真开始时刻,系统处于平衡状态,目标是控制定点浮空气球进行一定范围的机动调整。

浮空气球初始高度为20 000 m;轨迹控制器水初始高度为13 000 m;系绳长度为7 000 m。大气风场采用汕头地区三月份统计模型。图6给出了不同机动的仿真结果。

仿真结果表明:定点浮空气球在飞行过程中,其位置和速度按照控制目标进行变化,能够实现特定区域的定点驻留和机动飞行,但系统的机动调整时间较长。由于东西方向是通过调节浮空气球运行在“准零风层”高度上下反向风场中实现其定点控制,是一种间接控制,因此,其控制精度相对南北方向较差。

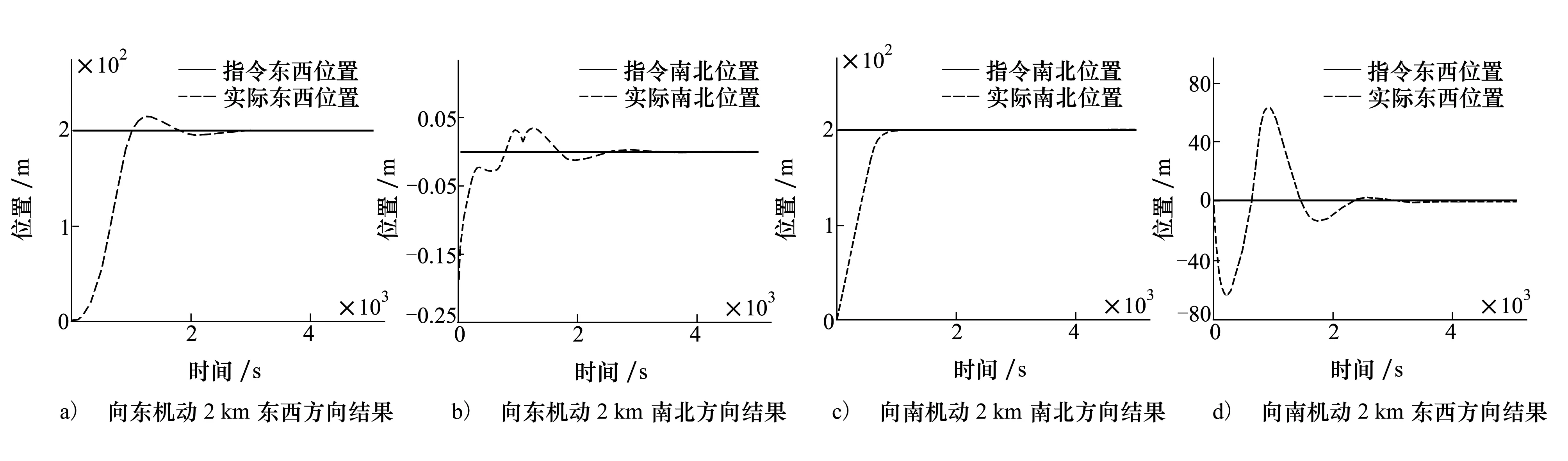
图6 机动调整仿真结果

6 结 论

本文针对平流层飞艇定点控制过程中能耗过高的问题,借鉴Global Aerospace公司平流层卫星的轨迹控制思想,通过修改控制结构和控制器件,利用平流层底部准零风层上下纬向风向发生反向,经向风速较小的特点,提出了一种新型的平流层浮空器定点部署方案。

论文通过对气象数据及相关资料的统计获取不同地域的准零风风场模型,完成了系统方案设计,建立了浮空气球、轨迹控制器和系绳组成的多体动力学模型,并进行了仿真验证。

仿真结果表明:

1) 利用平流层底部特殊风场特性的定点浮空器方案,能够实现特定区域的定点驻留和机动飞行。

2) 本文建立的模型能够基本反映浮空气球、系绳、轨迹控制器之间的相关关系,并能够反映系绳的姿态位置变化。

3) 由于控制系统中纬向和经向存在耦合,因此,东西方向定点精度相对较低。后续工作应当研究现代控制方法,并考虑控制时延和柔性形变等问题。

参考文献：

[1] Khoury G A, Gillett J D. Airship Technology[M]. London: Cambridge University Press,1999

[2] 常晓飞,杨韬,符文星,闫杰. 平流层卫星的建模与控制系统设计[J]. 哈尔滨工业大学学报,2012,44(9):682-686

Chang Xiaofei, Yang Tao, Fu Wenxing, Yan Jie. The Design of Trajectory Controller Based on Variable Structure Control with Sliding Mode for Stratospheric Satellite[J]. Journal of Harbin Institute of Technology, 2012, 44(9): 682-686 (in Chinese)

[3] Belmont A D, Dartt D G, Nastrom G D. Variations of Stratospheric Zonal Winds 20～65 km 1961～1971[J]. Journal of Applied Meteorology, 1975, 14: 585-594

[4] 吕达仁,孙宝来,李立群. 零风层与我国首次高空气球停留试验[J]. 目标与环境特性研究,2002,22(1):45-51

Lü Daren, Sun Baolai, Li Liqun. Zero Wind Layer and the First Dwell Experiment of High-Altitude Ballon in China[J]. Target Environment Feat, 2002, 22(1): 45-51 (in Chinese)

[5] 肖存英,胡雄,龚建村,刘佳. 中国上空平流层准零风层的特性分析[J]. 空间科学学报,2008,28(3):230-235

Xiao Cunying, Hu Xiong, Gong Jiancun, Liu Jia. Analysis of the Characteristics of the Stratospheric Quasi-Zero Wind Layer Over China[J]. Chinese Journal of Space Science,2008,28(3):230-235 (in Chinese)

[6] 陶梦初,何金海,刘毅. 平流层准零风层统计特征及准两年周期振荡对其影响分析[J]. 气候与环境研究,2012,17(1):92-102

Tao Mengchu, He Jinhai, Liu Yi. Analysis of the Characteristics of the Stratospheric Quasi-Zero wind Layer and the Effects of the Quasi-Biennial Oscillation on It[J]. Climatic and Enviromental Research, 2012,17(1): 92-102 (in Chinese)

[7] Morris Ray J, Hoffner Josef, Luebken Franz-Josef. Experimental Evidence of a Stratospheric Circulation Influence on Mesospheric Temperatures and Ice-Particles during the 2010-2011 Austral Summer at 69°[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2012, 89: 54-61

[8] Cathey Jr, Henry M. Evolution of the NASA Ultra Long Duration Balloon[C]∥AIAA Balloon Systems Conference, Williamsburg, 2007: 1-13

[9] Chung Soonjo, Kong E M, Miller D W. Dynamics and Controls of Tethered Formation Flight Spacecraft using the Spheres Testbed[C]∥AIAA Guidance Navigation and Control Conference and Exhibit, San Francisco, California, 2005:1-26

[10] Zeng F, Allen R. Evaluation of the Effects of the Communication Cable on the Dynamic of An Underwater Flight Vehicle[J]. Ocean Engineering, 2004, 31: 1019-1035

[11] 王飞. 海洋勘探拖曳系统运动仿真与控制技术研究[D]. 上海:上海交通大学,2006

Wang Fei. Simulation and Control Research of Marine Towed Secismic System[D]. Shanghai: Shanghai Jiaotong University, 2006 (in Chinese)

[12] Paul Williams. Electrodynamic Tethers Under Forced-Current Variations Part I: Periodic Solutions for Tether Librations[J]. Journal of Spacecraft and Rockets, 2010, 47: 308-319

[13] 常晓飞. 临近空间可定点气球系统的建模与控制研究[D]. 西安:西北工业大学,2010

Chang Xiaofei. Modeling and Controlling for the Near Space Stationary Balloon System[D]. Xi′an: Northwestern Polytechnical University, 2010 (in Chinese)