基于扩张状态观测器的再入弹头控制系统设计

徐珂文，高晓冬，赵红超，王 洁

（1.海军航空工程学院七系，山东烟台264001；2.海军装备部兵器部，北京100841）

随着世界各国反弹道导弹能力的不断提高，尤其是美国的“国家导弹防御系统（TMD）”和“战区导弹防御系统（NMD）”的部署和发展，使得弹道导弹弹头的突防能力面临严竣的挑战。因此，一些军事强国也在不断发展自身的弹头突防技术。在各种突防措施中，弹头的再入机动是一种经济而有效的突防措施。弹头实施再入机动的控制装置主要包括气动舵面、侧喷发动机和变质心控制装置3种[1-4]。变质心控制装置与前2种控制装置相比具有一些显著优点，受到了国内外控制领域研究者的高度重视。在此方面美国和俄罗斯的研究已经比较成熟，近年来也吸引了国内越来越多的研究者们的关注，理论研究正在不断完善。

弹道导弹的弹头有自旋式的，也有非自旋式的。本文针对采用变质心控制装置的非自旋弹头的控制问题进行研究。变质心非自旋弹头的滚动通道利用差动副翼进行稳定控制，在俯仰和偏航通道利用2个沿不同方向运动的质量块p 和q 进行控制[3，5-7]。弹头的各个通道间存在较强的耦合作用，而且弹头在飞行中受到的外界干扰也比较大，只有采用鲁棒性强的先进控制方法对质量块运动进行控制，才能实现对弹头姿态和机动弹道的准确控制，提高落点精度。众所周知，滑模控制方法对系统的参数摄动和内部及外界干扰等具有强鲁棒性[8]，因而本文采用滑模控制方法设计非自旋弹头的控制系统。

为了解决强耦合与外界干扰等不确定量问题，前期的研究者常采用神经网络技术以对汇总不确定量或者其上界进行估计，取得了较好的控制效果[9-10]。然而，神经网络技术需要大量样本进行训练，在实际应用中存在着训练速度慢、局部极小值和泛化能力弱等缺陷，而且神经网络也增加了控制系统的复杂性。从工程应用的角度而言，希望控制系统简单实用。为此，我们采用简单有效的扩张状态观测器技术[11-13]对各种不确定量进行估计和补偿，避免了利用神经网络技术进行估计的复杂性。本文将扩张状态观测器与滑模控制相结合，设计了一种简单实用的非自旋弹头的控制系统。

1 非自旋弹头的运动模型

由于弹头再入段飞行时间比较短，因而地球自转对弹头的影响非常小，可以忽略。非自旋弹头的滚动通道利用差动副翼进行稳定控制，故有：

将俯仰通道和偏航通道之间的耦合项以及外界干扰都看作是不确定项，弹头的俯仰通道和偏航通道的运动模型可转变为如下的简洁形式[4]：

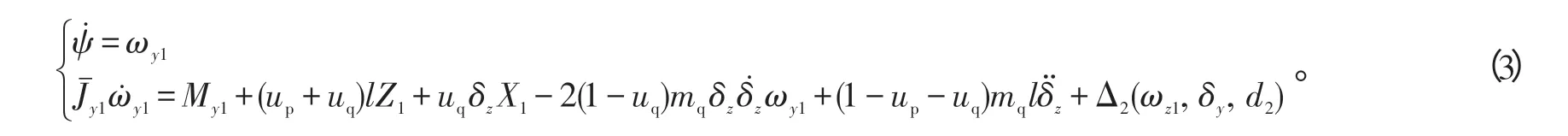
式（2）～（3）中：

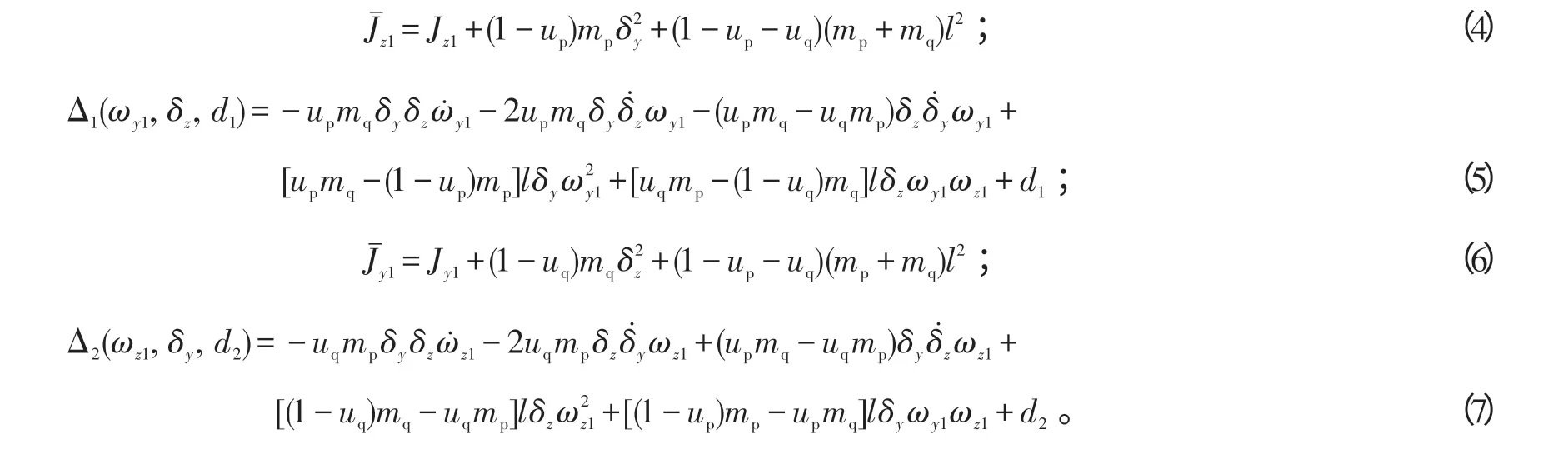
式（1）～（7）中：γ为滚动角；ωx1为滚动角速度；φ为俯仰角；ωz1为俯仰角速度；ψ为偏航角；ωy1为偏航角速度；d1、d2表示干扰影响；Δ1(ωy1,δy,d1)、Δ2(ωz1,δy,d2)称为“汇总不确定量”，它们包含了耦合项及外界干扰等因素；质量块p的运动加速度δy和质量块q的运动加速度δz分别为俯仰通道和偏航通道的控制输入量；φ 和ψ为输出量；其他符号的含义参见文献[4]。

2 弹头控制系统设计

控制系统的任务是控制弹头的输出量准确地跟踪预定的指令信号，即操纵输出跟踪误差收敛到零。弹头具有轴对称气动外形，其俯仰通道和偏航通道是基本相同的，下面先设计俯仰通道的控制系统。

俯仰通道的运动模型为式（2），选取状态量为：x1=φ，x2=ωz1；输入量为：u1=；将式（2）变换为一般的非线性系统形式：

式（8）中：

f1(x)和g1(x)为已知连续函数；w1(x)为未知连续函数。

对于汇总不确定量w1(x)，可以作为未知的被扩张的状态变量：x3=w1(x)，并设x˙3=ς(x)，其中ς(x)是未知函数；由此将式（8）变换为：

采用如下的扩张状态观测器进行估计：

总而言之，对于土木工程建筑而言，结构设计的合理性，不仅是关系到整个工程质量的重要因素，也是影响到建筑使用安全的关键因素，是保证建筑工程安全、有序施工的重要前提。虽然在当前社会中，建筑结构设计还存在一些问题，但是，随着建筑行业的发展，设计人员只要也积极地完善自身的综合素质，促进自身设计水平的提高，那么这些问题也都会迎刃而解。

式（13）中：β01,β02,β03＞0，0＜h＜1；fal 函数式为

根据文献[12]的研究，选择适当的观测器参数h、β01、β02、β03，就可以使z1、z2、z3分别收敛到实际状态x1、x2、x3的小邻域内，从而实现了对汇总不确定量x3的估计。一般地，可选取参数β01、β02、β03为：

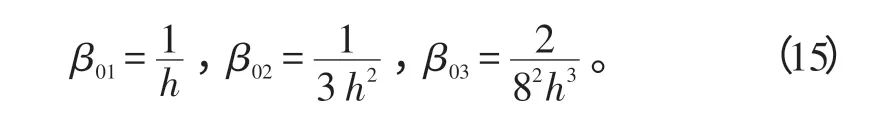
因此，只须选好参数h 即可。

下面再设计滑模控制器，定义系统跟踪误差为

式中，y1com为俯仰角指令信号。选取滑模面为：

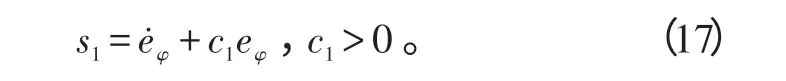
对上式求导，并与式（12）联立可得：

为了保证系统轨迹在有限时间内到达滑模面，并且在到达过程中具有良好的动态品质，采用如下的指数型趋近律：

联立式（17）、（18），且以观测器输出z3代替x3，则控制器设计为：

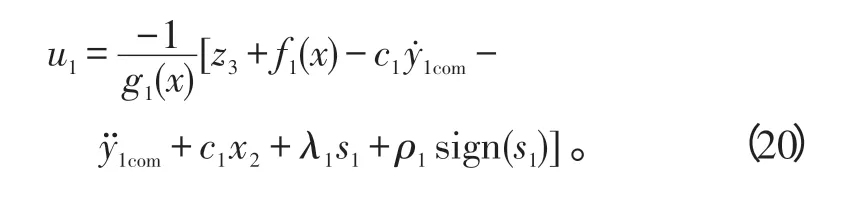
同理，偏航通道的运动模型式（3）变换为如下的一般形式：

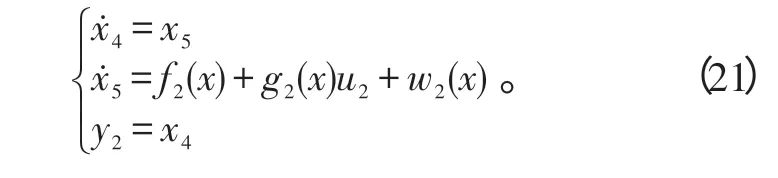
采用扩张状态观测器对w2(x)进行估计，类似于式（13），观测器的状态量为z4、z5、z6；在此基础上，偏航通道的控制器设计为

式（22）中：eψ=y2-y2com，s2=e˙ψ+c2eψ，c2＞0，λ2＞0，ρ2＞0，y2com为偏航角指令信号。该控制器能够完成偏航通道控制系统的任务。

3 仿真分析

为了检验基于扩张状态观测器的滑模控制器的控制性能，下面对某型非自旋再入弹头的变质心控制系统进行仿真分析。弹头的参数见文献[4]，仿真中，设外界干扰分别为：d1=1.25 sin(6t)、d2=1.25 cos(5t)，设弹头的初始姿态为：φ0=-40°、ψ0=0°，俯仰角和偏航角的指令信号分别为：y1com=-40°+5°sin(π t)、y2com=5°sin(πt+π/5)。俯仰通道的控制器设计为式（20），偏航通道的控制器设计为式（22）。经过仿真调试，选取控制系统参数分别为：c1=3.2、λ1=20、ρ1=3.0、c2=2.8、λ2=18、ρ2=3.5、h=0.01。控制系统的输出跟踪结果如图1、2所示。

由图1、2的仿真结果可得，俯仰角误差减小到1%以内的时间为0.78 s，偏航角误差减小到1%以内的时间为1.53 s，由于初始时刻偏航角误差比俯仰角误差大很多，因而减小到1%以内的时间也就多，俯仰角输出和偏航角输出对它们的指令信号的跟踪精度均达到了99.9%。上述仿真结果表明，所设计的基于扩张状态观测器的滑模控制器能够有效地补偿通道间耦合和外界干扰的影响，使控制系统输出快速而准确地跟踪上指令信号，具有较高的控制精度和鲁棒性。

图1 俯仰角输出跟踪曲线Fig.1 Tracking curve of pitch angle output

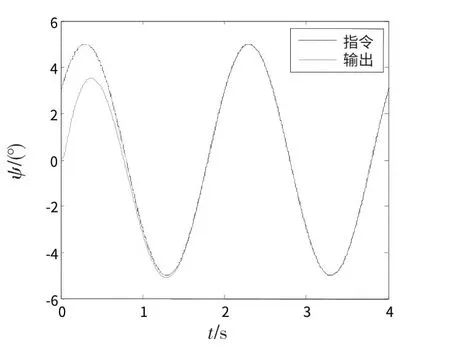
图2 偏航角输出跟踪曲线Fig.2 Tracking curve of yaw angle output

4 结束语

本文对采用变质心控制装置的非自旋弹头的姿态控制系统进行了研究。在建立姿态运动模型时考虑了俯仰通道和偏航通道之间的耦合作用及外界干扰的影响，并将这些因素综合为汇总不确定量。采用扩张状态观测器对汇总不确定量进行估计和补偿。为了提高控制系统的鲁棒性，采用了滑模控制方法设计了俯仰通道和偏航通道的控制系统中的控制器。对某型非自旋再入弹头的变质心控制系统进行仿真分析，仿真结果表明，所设计的基于扩张状态观测器的滑模控制器具有较高的控制精度和鲁棒性。

[1]WHITACRE W.Rigid body control using internal moving mass actuator[EB/OL].（2003-03-17）[2014-05-10].http：//www.aoe.vt.edu/～cwoolsey/Advisees/Under-graduate/Whitacre VSGCPaper.pdf.

[2]MENON P K，SWERIDUK G D，OHLMEYER E J，et al.Integrated guidance and control of moving mass actuated kinetic warheads[J].Journal of Guidance，Control，and Dynamics，2004，27（1）：118-126.

[3]李瑞康.再入体变质心动力学建模与仿真问题研究[D].哈尔滨：哈尔滨工业大学，2006.

LI RUIKANG.Study on dynamics modeling and simulation for moving mass reentry vehicle[D].Harbin：Harbin Institute of Technology，2006.（in Chinese）

[4]赵红超.变质心控制技术在再入弹头中的应用研究[R].烟台：海军航空工程学院，2010：3-8.

ZHAO HONGCHAO.Research on the application of variable centroid control technique to reentry warhead[R].Yantai：Naval Aeronautical and Astronautical University，2010：3-8.（in Chinese）

[5]熊先泽，张科，李言俊.高超音速导弹的新型控制模式研究[J].测控技术，2008，27（1）：88-90，98.

XIONG XIANZE，ZHANG KE，LI YANJUN.A new control method’s researching of supersonic speed missile[J].Test and Control Technoloty，2008，27（1）：88-90，98.（in Chinese）

[6]林鹏，周军，周凤岐.变质心再入飞行器的质心移动方式研究[J].火力与指挥控制，2009，34（2）：40-43.

LIN PENG，ZHOU JUN，ZHOU FENGQI.Research on centroid moving mode of moving centroid reentry vehicles[J].Fire Control &Command Control，2009，34（2）：40-43.（in Chinese）

[7]高长生，李瑞康，荆武兴.新型制导律在变质心再入飞行器中的应用[J].哈尔滨工业大学学报，2009，41（3）：6-10.

GAO CHANGSHENG，LI RUIKANG，JING WUXING.Application of a new guidance law in moving-mass reentry vehicle[J].Journal of Harbin Institute of Technology，2009，41（3）：6-10.（in Chinese）

[8]余名哲，张友安，吴华丽.基于滑模自适应控制的不确定混沌系统修正函数投影同步[J].海军航空工程学院学报，2014，29（2）：101-104.

YU MINGZHE，ZHANG YOUAN，WU HUALI.Modified function projective sysnchronization base on sliding mode adaptive control for chaotic systems with uncertainties[J].Journal of Naval Aeronautical and Astronautical University，2014，29（2）：101-104.（in Chinese）

[9]贺有志，李君龙.神经网络在质量矩导弹控制系统上的应用[J].系统工程与电子技术，2005，27（1）：93-96.

HE YOUZHI，LI JUNLONG.Application of neural network in control system of moving mass missile[J].Systems Engineering and Electronics，2005，27（1）：93-96.（in Chinese）

[10]ZHAO H C，CHEN J，LIU H Z.RBF neural networkbased terminal sliding mode control for reentry warhead[J].Applied Mechanics and Materials，2011：63-64，381-384.

[11]HAN J.From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics，2009，56（3）：900-906.

[12]韩京清.自抗扰控制技术[M].北京：国防工业出版社，2008：210-229.

HAN JINGQING.Active disturbance rejection control technique[M].Beijing：National Defense Industry Press，2008：210-229.（in Chinese）

[13]XIA Y，ZHU Z，FU M.Back-stepping sliding mode control for missile systems based on an extended state observer[J].IET Control Theory and Applications，2011，5（1）：93-102.