(C,α,ρ,d)-V-凸多目标变分问题的混合对偶性

张永战， 张庆祥

(1.定边中学， 陕西 榆林 719000；2.延安大学 数学与计算机科学学院， 陕西 延安 716000)

0 引 言

有关数学规划和变分问题的关系，Hanson[1]在1964年做出了开创性的研究，随后一些学者开始相继对变分问题进行了研究[2-4]。C.Nabak和S.Nanda[3]在(F,ρ)凸条件下建立了变分控制问题的对偶理论。后来I.Ahmad和S.Sharma[4]在(F,α,ρ,θ)-V-凸性条件下研究了多目标变分问题的混合对偶性。

本文将D.H.Yuan[5]提出的(C,α,ρ,d)-凸函数，推广到(C,α,ρ,d)-V-凸，并研究多目标变分问题的混合对偶性。同时Wolfe型对偶和Mond-Weir型对偶是这种混合对偶性的特殊情况。得到弱对偶性与强对偶性定理，进一步推广文献[5]中的结论。

1 概念与引理

考虑如下多目标变分问题(VP)：

s.t.x(a)=α,x(b)=β,

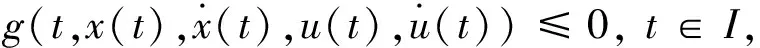
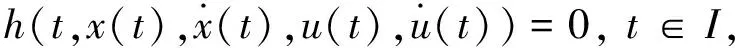
其中I=[a,b]为实空间，令X表示(VP)的可行域，即

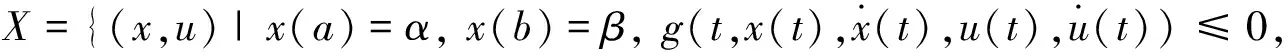
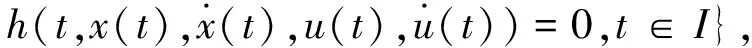
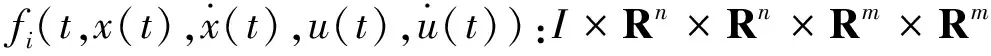
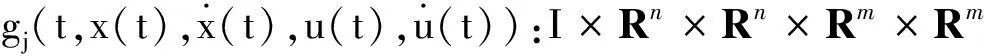
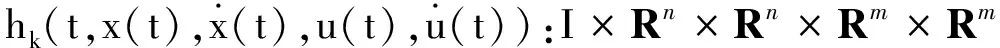
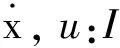
∀i∈P。

下面我们给出几类新的广义凸函数的定义。

对任意的a1,a2∈Rn均成立。

在本文我们总假定C(·,·,·,·,·,·,·,·,·)(0)=0。

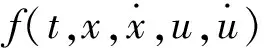
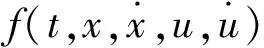
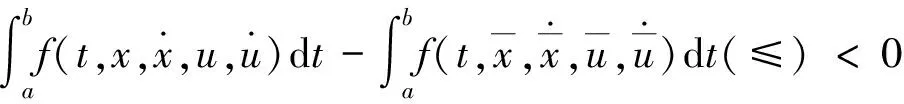
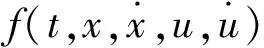
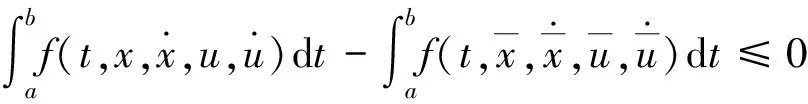
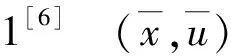
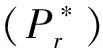
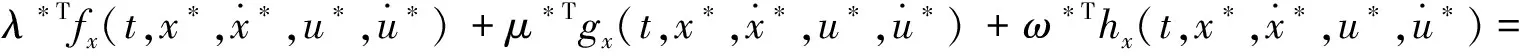
2 对偶定理

设J1是M的子集且J2=MJ1，K1是N的子集且K2=NK1，考虑(VP)的如下混合对偶问题：

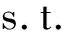
(5)

(6)

(7)

在(DVP)中当J1=∅且K1=∅时，即可得到Mond-Weir型对偶，当J2=∅且K2=∅时即可得到Wolfe型对偶。

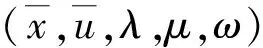
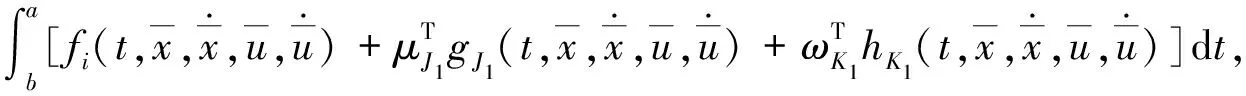
(8)

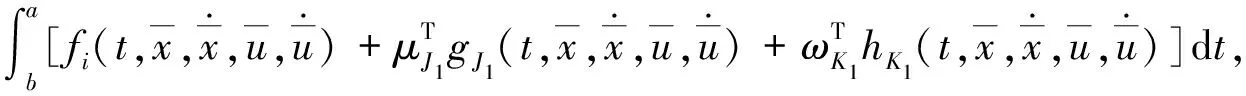
(9)

证明假设定理不成立，由(8)，(9)两式及(3),(4),(7)式得，

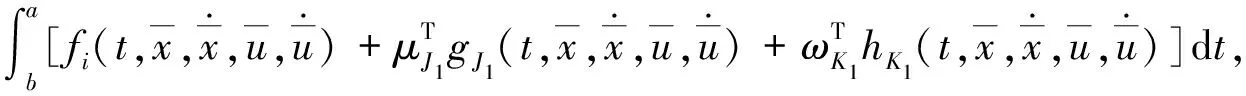
(10)

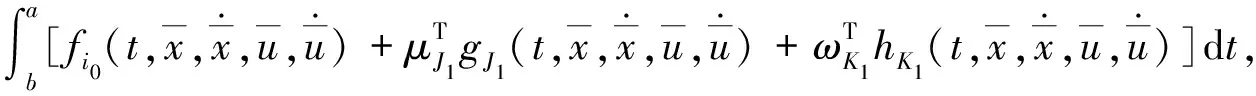
(11)

于是有

(12)

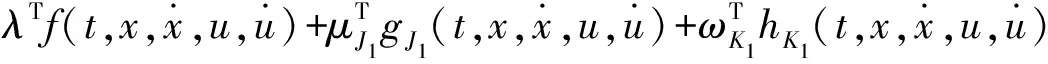
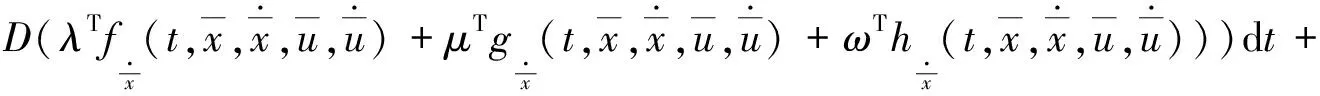
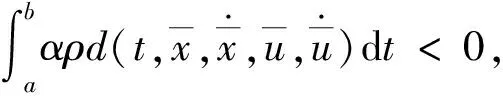
另外，由(5)式及C(·,·,·,·,·,·,·,·,·)(0)=0，即有

这与d：I×X×X×Y×Y→R+,α：X×X×Y×Y→R+{0}且ρ>0导出矛盾。

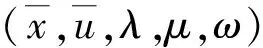
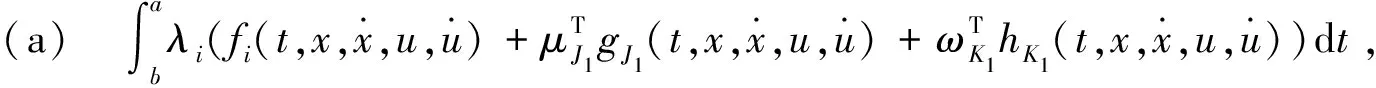
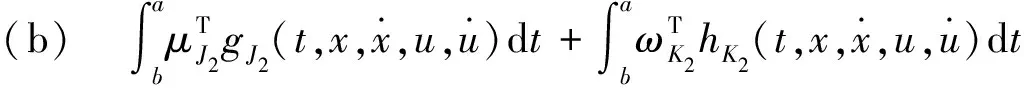
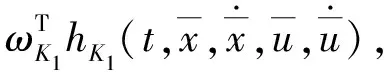
(13)

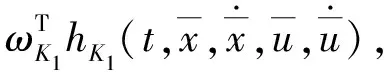
(14)

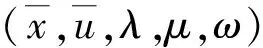
因此

由假设(b)可得

(15)

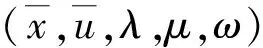
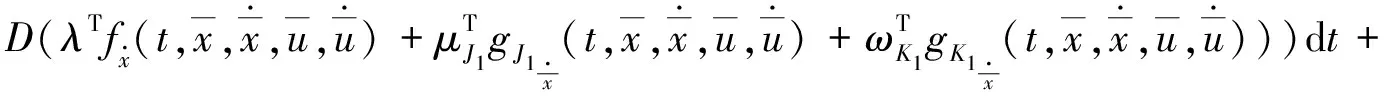
(16)

再由(15)、(16)式得

(17)

另一方面，假设定理结论不成立，则(13)与(14)式成立，由假设(a)，得

从而

(18)

此式与(17)式矛盾。

[参考文献]

[1] HANSON M A.Bounds for functionally convex optimal control problem[J].J.Math.Anal.Appl.,1964(8)：84-89.

[2] 陈世国,祁传达.多目标变分问题的混合对偶性[J].数学的实践与认识,2003,33(12)：97-102.

[3] NABAK C,NANDA S.On efficiency and duality for multiobjective variational control problems with (F,ρ)-convexity[J].J.Math.Anal.Appl.,1997,209：415-434.

[4] AHMAD I,SHARMA S.Sufficiency and duality for multiobjective variational control problems with generalized (F,α,ρ,θ)-V-convexity[J].Nonlinear Analysis,2010,72：2564-2579.

[5] YUAN De-hui,LIU Xiao-ling,CHINCHULUUN A,et al.Nondifferentiable Minimax Fractional Programming Problems with (C,α,ρ,d)-Convexity[J].J.Optim.Theory Appl.,2006,129(1)：185-199.

[6] PREDA V.On efficiency and duality for multiobjective programs[J].J.Math.Anal.Appl.,1992,166：365-377.

[7] BHATI D,MEHRA A.Optimality conditions and duality for multiobjective variational problems with generalized B-invexity[J].J.Math.Anal.Appl.,1999,234：341-360.

[8] 陈世国,刘家学.具V-不变凸性的一类多目标控制问题的混合对偶性[J].数学杂志,2010,30(2):338-344.

[9] 陈世国,刘家学.具广义V-不变凸多目标变分的混合对偶性[J].大学数学,2011,27(1):101-105.