用斜交坐标轴画二维对称时空图
党兴菊,张 瑶,吴文良
(昭通学院物理与电子信息工程学院,云南昭通 657000)
传统的二维时空图习惯上将基本坐标系的空间坐标轴和时间坐标轴画得相互垂直,如文〔1〕-〔7〕都是如此。但在这样的时空图中其他惯性坐标系的空间轴和时间轴不可能再画得垂直,并且任意两个不同的坐标系的坐标轴上的单位长度表示的物理量也不相等,即传统的时空图画法并不对称,或许正是这一原因,时空图在狭义相对论学习中的重要性并未引起足够的重视,如文献〔8〕-〔11〕等普通物理或大学物理教材在介绍狭义相对论时都未介绍时空图。针对这种情况,2008年黄献民先生给出了一个在形式上完全对称的时空图,并建议读者在读懂了相对论的时空几何的数理逻辑后,在讨论问题时采用对称结构的时空图,“因为这种形式更能体现相对论时空下的时空相对性和对称性”〔12〕。
遗憾的是,文〔12〕只给出了一个实例,而未给出这种对称形式时空图在普遍情形下的具体作图法,对“两个参考系的时空坐标的标度有相同的几何长度”的条件也未作讨论,学习者在应用中易出现错误和困惑。目前我们尚未发现对对称形式结构的时空图进行讨论的其他研究,也尚未见到另外有研究者运用过对称形式的时空图。为了能够在普通物理课程中就能较好地阐述狭义相对论,本文给出文〔12〕中所言对称形式时空图的一般作图法并对其展开了讨论。
1 对称形式的时空图的一般画法
文〔1〕所称对称形式的时空图,实质上是用斜交坐标轴来画时空图。尽管从理论上在闵氏空间中我们认为时间坐标与空间坐标是正交的,但我们在画时空图时,画出来的时空坐标轴的夹角一般情况下不再是直角。应注意不能把这两件事混为一谈,在二维时空图中用斜交坐标轴来画图,并不改变时空坐标的正交性。
用斜交坐标轴画二维时空图的具体做法是:在平面上用两条单位长度相同且以2α角相交于原点的数轴分别作为空间坐标轴x 和时间坐标轴t。通常使空间坐标轴沿水平方向并规定正向指向右方,且使 α ∈(0 ,π 2 ),例如可取 α=π 3。为了使两条数轴上单位长度代表的物理量量纲相同,根据光速不变原理,将时间t 乘以作为物理学常量的光速c,即让时间轴表示的量不是t 而是ct。这样两条轴上的单位长度表示的物理量的量纲就相同了。 例如,若时间轴上的单位长度表示的时间间隔是一年,则空间轴上同样的单位长度表示的空间距离为1光年。
接着在时空图上确定事件的坐标。两条数轴的公共原点表示某时刻T发生在空间某条直线x上某点O 的事件P,将该事件的坐标规定为(0,0);时间轴上的点表示不同时刻在O点发生的事件,时间轴亦即静止在O 点的观测者S 的世界线;空间轴上的点表示观测者S所认为的在同一时刻T发生在直线x上不同位置的事件。两条数轴所在的平面上的点表示各个时刻发生在直线x上的事件。其中平行于时间轴的直线上的不同的点表示同一位置不同时刻发生的事件,而平行于空间轴的直线上的点则表示同一时刻发生在直线x上不同位置的事件。所有这些都是相对于给定的观测者S而言的。这样,为了确定某一事件的坐标,只需过该点作两条数轴的平行线分别交另一条数轴于一点,由两个交点各自在数轴上的读数即确定了该事件的时空坐标。
现在我们考虑沿着直线x传播且在时刻T通过坐标原点O 的光。根据前述作图法,无论α如何取值,这束光在时空图上都用两条数轴所构成角的两条角平分线之一表示,而另一条平分线则表示沿相反方向传播的光。我们把坐标轴的这两条角平分线称为光锥。α正是两条坐标轴与某条光锥所成的夹角。
现在考虑在时刻T与S重合于O且相对于S沿x轴正向以速度v 作匀速直线运动的观测者S′,显然S′的世界线为过原点的一条有向直线,该直线与时间轴ct轴的夹角β取决于v和α。见图1。
在图1 中,设 A 点在 S 系所表示的时刻为 t,则OA=ct,AB=vt。由于 OA 和 AB 上单位长度相同,对△OAB应用正弦定理,有

特别地,当v=c时,
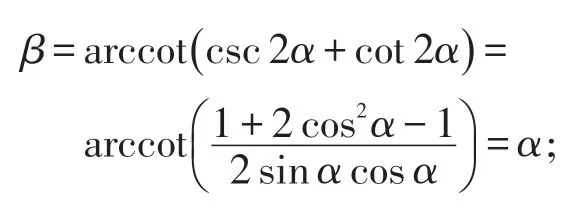
而当 v =-c 时 β=arccot( )-csc 2α+cot 2α =知光锥确实为两条数轴的角平分线。
显然,有向直线OB即为S′的世界线,亦即参照系S′的时间轴ct′。根据光速不变原理,空间轴x′必须使得S 系的光锥同样成为S′系的光锥,即它必须成为ct′与x′两条轴的角平分线。于是x′轴就是ct′轴关于正向光锥的镜像对称。需要注意的是,OB线上的单位长度与OA线上的单位长度并不一定代表相同的时间间隔,即OA 线上代表1 a 的1 cm 在OB线上并不一定同样代表着1 a。
那么,需要满足什么样的条件,OB线上的单位长度才与OA线上的单位长度表示相同的时间间隔呢?根据洛伦兹变换,如果OB线上的单位长度与OA线上的单位长度表示相同的时间间隔,则有OA=γOB。其中而由前述:于是
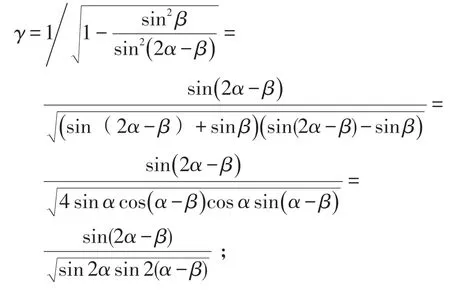
另一方面,显然由图1中应用正弦定理可知OA/OB=sin(2α-β)/sin(π-2α),于是应有

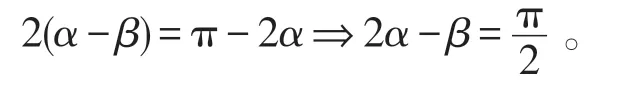
即S′系的时间轴ct′须与S系的空间轴x轴垂直。与此相应,S′系的空间轴x′轴则须与S 系的时间轴ct垂直。这样画出的一对参照系可称之为共轭参照系,其时空图为对称时空图,其特点是这两对坐标轴上的单位长度所表示的物理量相等。图1给出的正是这样的一对共轭坐标系,文献〔1〕中所给出的对称时空图也同样是一对共轭参照系。据此我们得到对称时空图的具体作图法如下。
作沿水平方向指向右方的数轴为S系的空间坐标轴x,作沿竖直方向指向上方的数轴为S′系的时间坐标轴ct′,两条数轴的公共原点代表S和S′重合的位置和时间。根据S′系相对于S 的速度(沿x 轴方向)v确定S系的时间坐标轴ct′,使ct轴与ct′轴的夹角β=arcsin(v/c),当v>0时ct轴在ct′轴的左侧,否则在右侧。ct轴与x轴的两条角平分线为所有惯性参照系的共同光锥,分别代表在0 时刻经过坐标轴原点的沿x轴正向和负向传播的光。根据光锥确定S′系的空间坐标轴x′。这样画出的时空图即为对称时空图,其特征是4 条坐标轴上的相同长度都代表着相同的时空距离。
2 不同惯性参照系坐标轴上表示单位时空间隔的单位长度
由以上讨论可见,选定了某一参考系S后,对某一相对于S 以速度v0作匀速直线运动的惯性系S′,都可画成与S 共轭的坐标系,而其他的惯性系如S″则不可能再与它们共轭,即S 坐标系和S″坐标系的坐标轴上的单位长度并不相同。现在我们讨论:不同参照系中同样的一个空间尺度比如1 光年,如果在x 轴上用1 cm 表示,则在x″轴上需要要用多少厘米表示。假设需要用y cm 表示,则y 与S″坐标系相对于S 系的速度v 构成函数关系,且这一函数关系应该使得当v等于0或者v0时,y都等于1。
计算方法如下:如图2,设ct″轴与ct轴成β角,在ct 轴上取 OE=1 cm,作 EC 平行于光锥交ct″轴于 C,再作CD 平行于另一条光锥交ct 轴于D,设线段OC表示的时间是S″系中的k a,于是OD=k2cm。作CF平行于 x 轴交 ct 轴于 F,则 EF=ED/2=(k2-1)cm/2。由于△ECD 为直角三角形,而CF 为其斜边上的中线,故 CF=(k2-1)cm/2。但 CF=(v/c)OF=(v/c)(OE+EF)=(v/c)(k2+1)cm/2。所以(v/c)(k2+1)=k2-1。从而可得这正是光的多普勒效应的计算公式。
由作图可知,
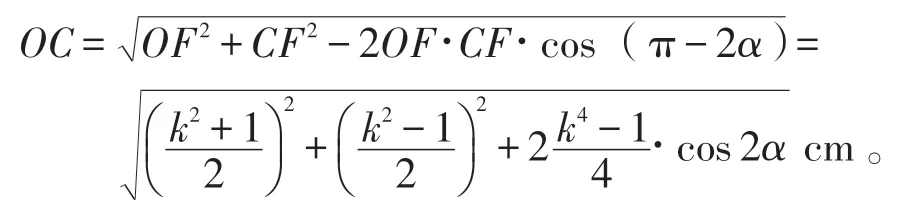
由于OC 表示的时间是S″系中的k a,而S″系中的 1 a 用 ct″轴上的 y cm 表示,所以 OC=ky cm。故

图2 不同坐标系中的单位长度

从而
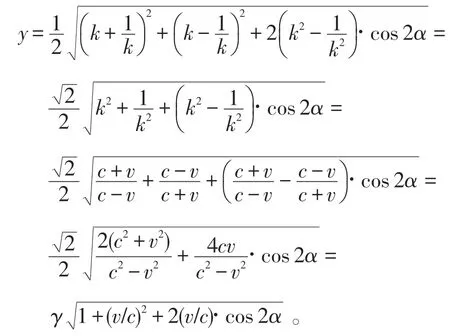
显然,v=0时,y=1。当v=v0时,-cos 2α,
可见公式
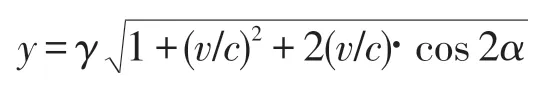
满足前述要求。
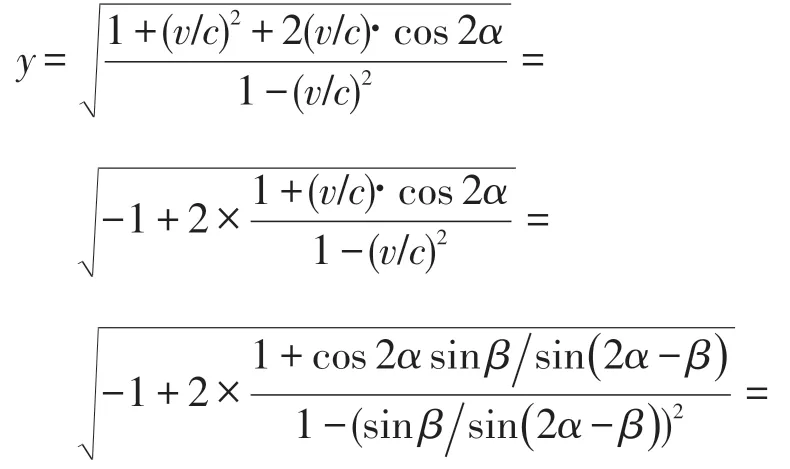
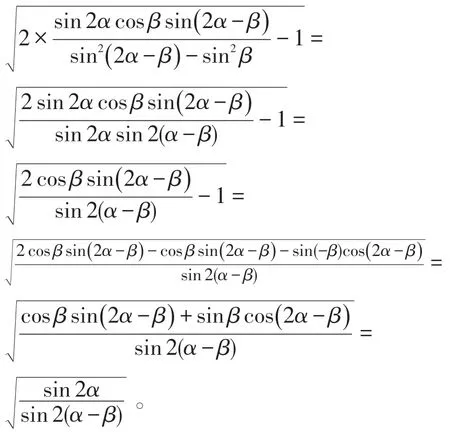
下面我们讨论y 的极值。显然当α →β 即v→c时,y→∞没有极大值;而当即时y 有极小值,此时 v/c=tan(α-π/4)。图3 给出了当时单位点依赖于β的轨迹。

图3 单位点的轨迹
这样我们就对二维时空图有了一个较为清晰和完备的认识,并且明白了在仅讨论一对相互作匀速直线运动的物体的运动时,应按共轭坐标系将时空图画成对称的形式,以便直接利用几何知识求出相关物理量。
3 用对称时空图导出相对论速度变换公式
作为应用,下面我们用对称时空图导出相对论速度变换公式。
如图4作对称时空图。设S′系相对于S以速度v 沿x 轴方向作匀速直线运动,S′相对于S 以速度u沿x轴方向作匀速直线运动,S″相对于S′的速度为u′,直线OC为S″的世界线。则有:

注意 AB、AC 平行于 x 轴,而 CD 平行于 x′轴,因而垂直于ct 轴。 由 ∠EDO 和 ∠BDC 为对顶角,知RtΔOED ~ RtΔCBD ,故
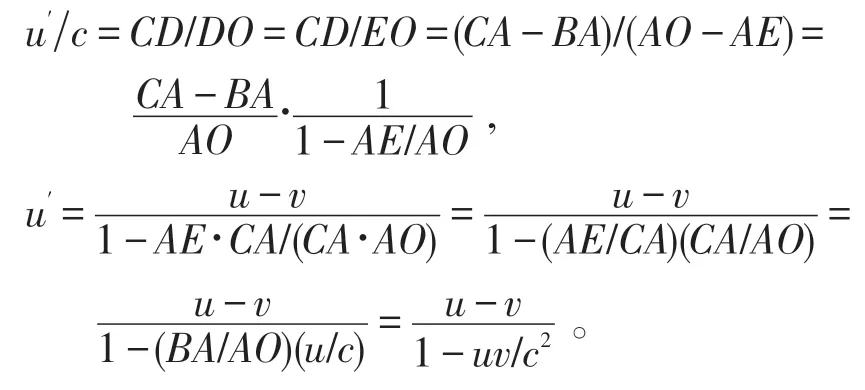

图4 速度变换公式的导出
此即一维相对论速度变换公式。
4 结语
传统的二维时空图习惯上使基本坐标系的时空坐标轴相互垂直,但其他惯性坐标系的时空轴不可能再画得垂直,并且对不同坐标系,同类坐标轴上的相同长度表示的物理量并不相等。本文根据几何知识和狭义相对论的基本原理提出:对称时空图中的两套坐标系,必须让一个坐标系的空间轴垂直于另一个坐标系的时间轴,而让时间轴垂直于另一个坐标系的空间轴。 在这样的时空图中尽管时空坐标轴是斜交的,但两个对称的坐标系中轴上相同长度代表着相同大小的物理量。此外,存在着这样一个坐标系,在它的坐标轴上表示单位物理量的长度最短。利用对称时空图,可以更方便地直接借助几何知识求解某些问题,以加深对狭义相对论的理解。
〔1〕王正行.在解题中学习近代物理〔M〕.北京:北京大学出版社,2004.
〔2〕REESE R L. University Physics〔M〕.北京:机械工业出版社,2003.
〔3〕DAVID B. The Special Theory of Relativity〔M〕. Redwood City:Addison Wesley Publishing Company,1965.
〔4〕郭启连,齐鲁祥.时空图对时钟佯谬诠释的应用〔J〕.德州学院学报,2004,20(4):25-27.
〔5〕梁灿彬,曹周键.《从零学相对论》连载④〔J〕.大学物理,2012,31(10):58-62.
〔6〕吕嫣,段家兴,图雅. 对双生子佯谬问题的几种解释〔J〕. 沈阳师范大学学报:自然科学版,2011,29(3):384-386.
〔7〕杨志万.闵氏几何法解析“双生子佯谬”及结果讨论〔J〕.大学物理,2012,31(9):27-29.
〔8〕梁绍荣,刘昌年,盛正华. 普通物理学(第一分册力学)〔M〕.3版.北京:高等教育出版社,2005.
〔9〕马文蔚,解希顺,周雨青.物理学:下册〔M〕.5版.北京:高等教育出版社,2006.
〔10〕朱峰.大学物理〔M〕.2版.北京:清华大学出版社,2008.
〔11〕程守洙,江之永.普通物理学:上册〔M〕.6版.北京:高等教育出版社,2006.
〔12〕黄献民.狭义相对论与时空图〔M〕.北京:国防工业出版社,2008.

