基于模糊集合理论评定ICP测量不确定度的研究

王　英　杨曙年

(1.华中科技大学机械科学与工程学院，武汉 430060；2.武汉市计量测试检定(研究)所，武汉 430050)

0　引言

测量不确定度用于描述被测量值的真值的估计范围。从测量不确定度的评定方法上讲，包括统计不确定度和非统计不确定度两类。对于统计不确定度而言，早已建立了相应的统计数学模型。测量结果扩展不确定度的评定方法目前主要采用的是统计评定方法。设服从正态分布的测量值x的概率密度为P(x)，用Bessel方法可得其扩展不确定度为ku，其中k为包含因子，u表示测量结果的标准不确定度(用测量数据样本的标准差来表征)。

在实际测量中，并非所有的扩展不确定度都可以用统计方法评定，因此，非统计不确定度的评定就显得非常重要。同时，总有一些比统计不确定度更复杂的情况。例如：在火箭发射试验、破坏性实验以及容易造成环境污染的试验中，测量数据非常少，其概率分布密度又未知。在这种情况下，用经典统计评定方法就显得非常困难。

为了解决这个问题，本文采用模糊可用区间直接求取扩展不确定度的方法。该方法允许测量数据的个数少，被测量的概率分布未知，且求得的扩展不确定度区间具有很高的包含概率。

1　测量值的模糊可用区间

模糊数学是用隶属函数研究具有模糊性的事物，探讨事物对某一模糊概念的隶属程度从真到假或从假到真两个极端的中间过渡的规律性。在测量过程中，被测量的真值(设为X0)总是客观、唯一存在的。因此，可以定义一个被测量真值的集合A为

A=(X0)

(1)

此时，集合A仅含有一个值(元素)X0。

由集合理论可知，实际测量值xi(i=1,2,…，n)和A满足下列关于二值逻辑的特征函数

(2)

在模糊数学中，xi对A的隶属关系可以被认为是一种过渡，表示xi接近X0的程度，过渡区间为B，可以用图1所示的下列隶属函数描述

(3)

式中，μi(x)∈[0,1]，i=1、2。由图1可知，μ1(x)是增函数，μ2(x)是减函数。

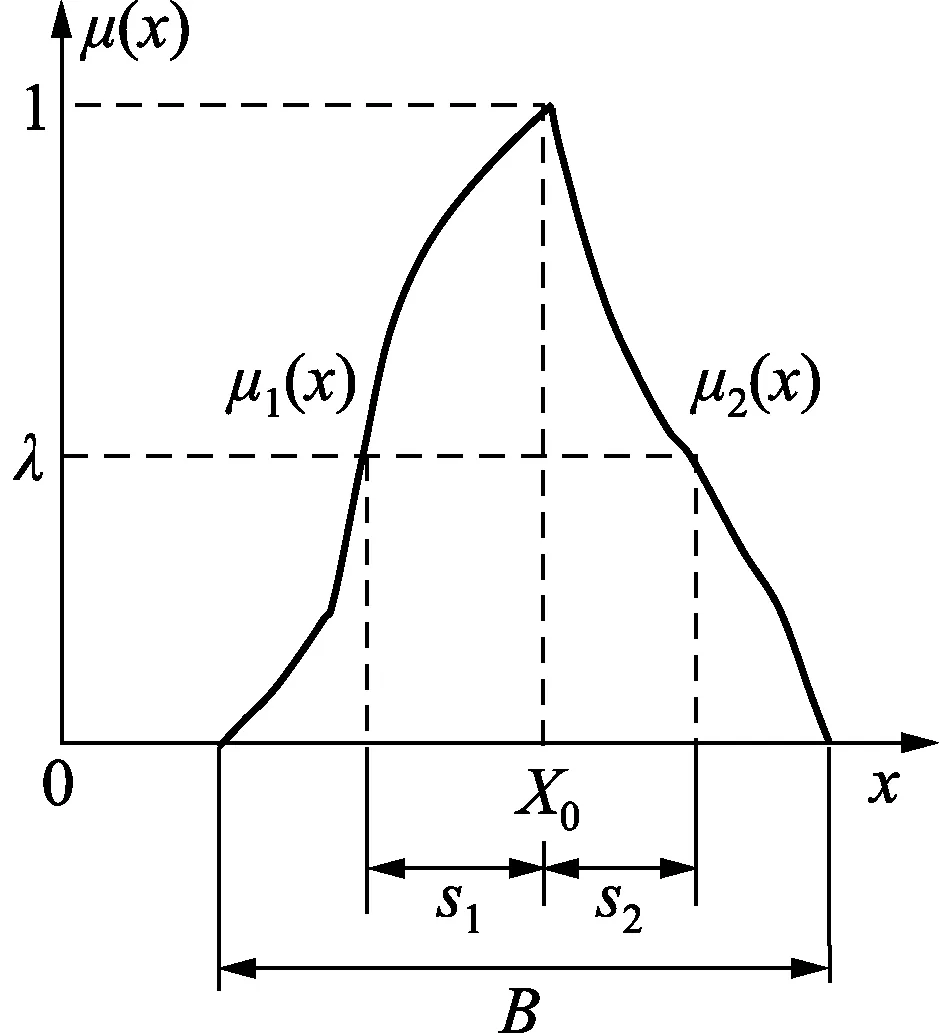
图1　隶属函数μ(x)

隶属函数μ(x)描述了测量值xi是如何符合集合A的。如图1，若取水平l，l∈[0,1]，相应地，在x轴上的X0两侧附近有两个区间s1和s2，则在隶属水平为l的前提下，x隶属于A的区间为

UFl=s1+s2

(4)

对所有测量值xi，若给定l=l*值，则UFl=UFl *唯一确定。即在隶属水平l*时，测量值xi相对真值X0的分散范围为UFl *。

区间B称为模糊区间，若l*为最优水平，则称UFl *为l*水平下的模糊可用区间。于是有下列表征真值的特征函数

(5)

式(5)表明：凡落在区间UFl *中的值都是可用的(为真)，否则不可用(为假)。

结合测量理论不难理解，可以用UFl *来表征测量结果的扩展不确定度。

2　l *和X0的确定

从模糊数学意义上讲，l*划定了事物从一个极端转变为另一个极端的界限。实际上也可以将l*看作一个模糊数，而模糊数为0.5时最具模糊性，即亦真亦假。当l≥0.5时，就意味着A中包含了几乎所有有用的x。因此，在逻辑上可将l*确定为0.5。在具体处理数据时，当测量值为有限个离散值时，一般取l*=0.4～0.5。当测量值个数n较小时，可以取l*=0.4。

一般而言，真值X0是未知的，可用数理统计中的数学期望或模糊数学中的模糊期望来估计。根据图1，本文用μ(x)=1时的x值来估计X0，即

X0≈x|μ(x)=1=xν

(6)

对于小样本容量的测量数据样本，用这种方法来估计X0是合理的。

3　参数的映射和求解

参数的映射的目的实际上就是将普通集合转换为模糊集合。

3.1　参数的映射

模糊数学中的隶属函数可用误差理论中的概率分布密度表征。如果已知概率密度函数Y=P(x)，通过线性变换

μ(x)=(P(x)-Ymin)/(Ymax-Ymin)

(7)

其中，Ymax≠Ymin。由此式将Y映射至[0，1]区间，就得到μ(x)。

由式(6)和式(7)可知，xν对应着最大概率分布密度值Ymax。

因为已将xi看作模糊数，故其对真值的隶属度应满足[0,1]区间。为此，通过线性变换

ην=(xν-xmin)/(xmax-xmin)

(8)

η(x)=(x-xmin)/(xmax-xmin)

(9)

t=t(x)

=|η(x)-ην|

=|x-xν|/(xmax-xmin)

(10)

将x映射在[0，1]区间，得到用模糊数t(x)表示的测量值。式中，xν可以用tν=0表示。

在区间[0，1]上，用ψFl表示UFl，用ξ1和ξ2分别表示s1和s2，式(4)就变为

UFl=s1+s2

=|x-xν|μ1(x)=l+|x-xν|μ2(x)=l

=(xmax-xmin)(t|μ1(x)=l)

+(xmax-xmin)(t|μ2(x)=l)

=(t|μ1(x)=l+t|μ2(x)=l)(xmax-xmin)

=(ξ1+ξ2)(xmax-xmin)

=ψFl(xmax-xmin)

(11)

这里

ψFl=ξ1+ξ2

(12)

于是，图1变为图2。

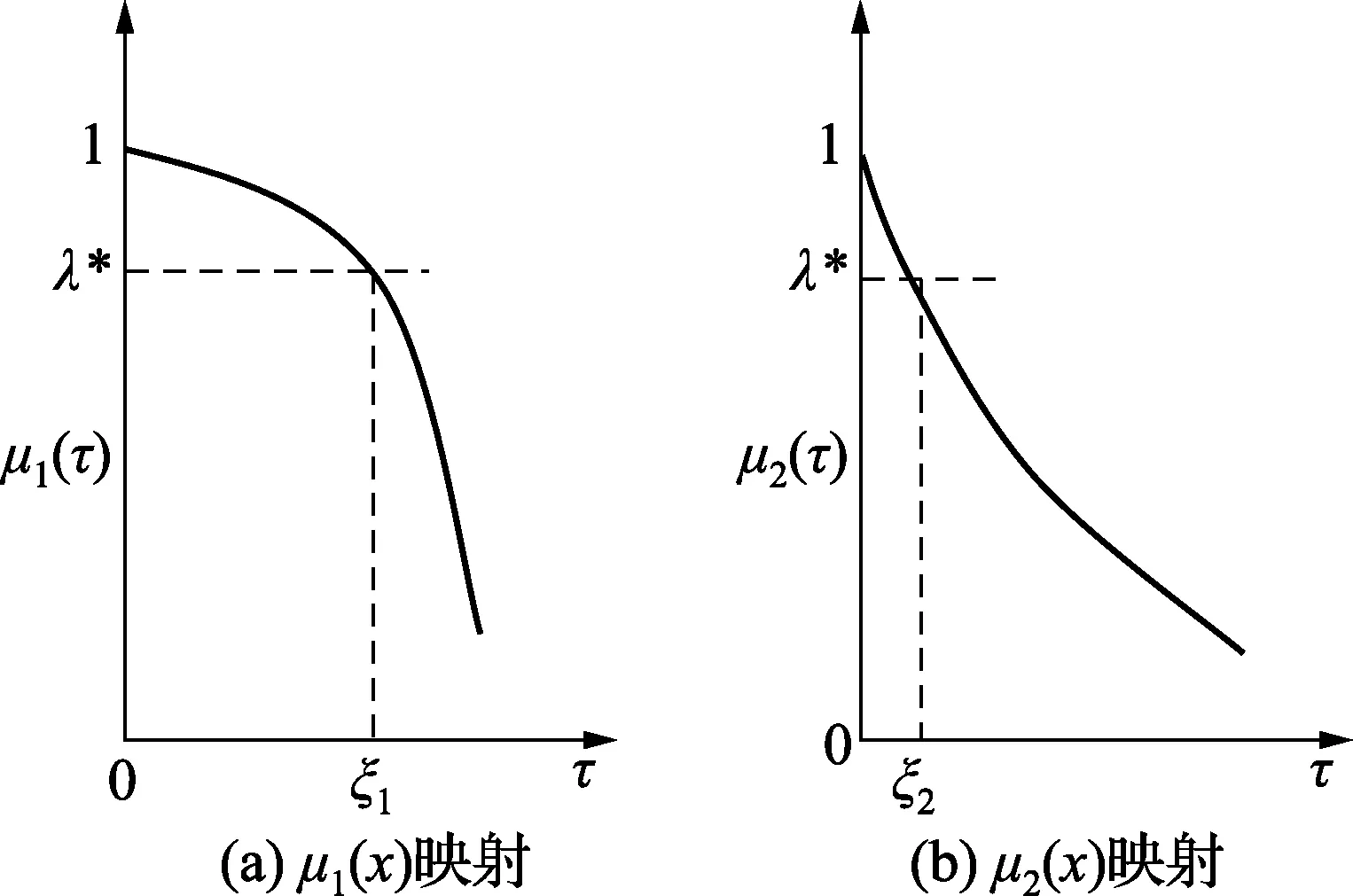
图2　参数映射

3.2　参数求解

若离散值μ1j(tj)和μ2j(tj)，j=1,2,…已知，就可以用下列方法求出μ1(t)和μ2(t)。

定义最大模范数

(13)

用正交多项式

(14)

(15)

分别逼近离散值μ1j(tj)和μ2j(tj)，就得到

μ1(t)=f1(t)

(16)

μ2(t)=f2(t)

(17)

设

r1j=f1(tj)-μ1j(tj)(j=1,2,…,ν)

(18)

r2j=f2(tj)-μ2j(tj)(j=ν,ν+1,…,n)

(19)

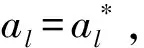
(20)

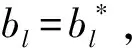
(21)

可求出待定系数al和bl。

在式(14)和式(15)中，多项式阶次L一般取3，即可获得较高的逼近精度。

式(20)和式(21)的约束条件分别为

f＇1=df1/dt≤0

(22)

和

f＇2=df2/dt≤0

(23)

式(22)和式(23)表明隶属函数本身的单调下降特性。

这种逼近方法叫做最大模范数最小法，研究表明，其逼近误差小于经典的最小二乘法。

最后按下列两式分别求解ξ1和ξ2

min|μ1(t)-l*|t =ξ1

(24)

min|μ2(t)-l*|t =ξ2

(25)

4　隶属函数的建立

4.1　直方图估计法

直方图估计法是一种常见的方法，当样本容量n值较大时，例如n≥30，可将测量值分成q组，每组的中值为dj，频率为mj。取频率为最大值的组中值为xν，该组组号设为ν(若有t个最大频率相等，可用算术平均值法确定xν和ν)，有

p1j(xj)=mj(j=1,2,…,ν)

(26)

p2j(xj)=mj(j=ν,ν+1,…,q+1)

(27)

4.2　线性估计法

将xi序列从小到大排列，形成新序列

(28)

定义

(29)

一般，Δi越小，测量值越密集；反之越疏松。即Δi和Δxi的分布密度有关。为此，假设线性隶属函数

mj=1-(Δj-Δmin)/Δmax

(30)

Δmax=maxΔj，Δmin=minΔj(j=1,2,…,n-1)

为近似的概率分布密度因子。和直方图估计法相类似，可以求出xν和ν，于是

(31)

(32)

然后由式(7)～式(23)即可求得μ1j(tj)、μ2j(tj)、μ1(t)和μ2(t)。用线性估计法确定隶属函数，一般要求n≥4。

5　算法描述

上述有关公式的求解，是以最优化理论为基础的。目标函数为式(20)、式(21)、式(24)和式(25)，约束条件为式(22)和式(23)，具体使用的优化方法是序贯无约束极小化技术SUMT(Sequential Unconstrained Minimization Technique)。扩展不确定度的评定步骤如下：

1)采样xi，i=1,2,…,n；

4)由式(7)获得μ1j(tj)(j=1,2,…,ν)和μ2j(tj)(j=ν,ν+1,…,n)之后，再用式(9)和式(10)计算η(x)和t；

5)用式(14)、式(15)、式(18)、式(19)、式(20)和式(21)创立数学模型f1和f2，约束条件为式(22)和式(23)；

6)通过式(16)和式(17)得到隶属函数μ1(t)和μ2(t)；

7)在借助式(24)和式(25)计算出l=l*水平下的ξ1和ξ2之后，用式(11)获得UFl *。

6　测量不确定度模糊评定的应用

现仍以经典评定中使用的电感耦合等离子体(ICP)发射光谱仪测量铜溶液浓度为例(参见《中国计量》2007年第6期)，在建立了式y=74.7947+3630.4492x标准曲线的基础上，测量浓度值为3.00μg·mL-1的铜标准溶液GBW(E)130079的浓度，按本文4的要求计算，结果列入表1和表2。

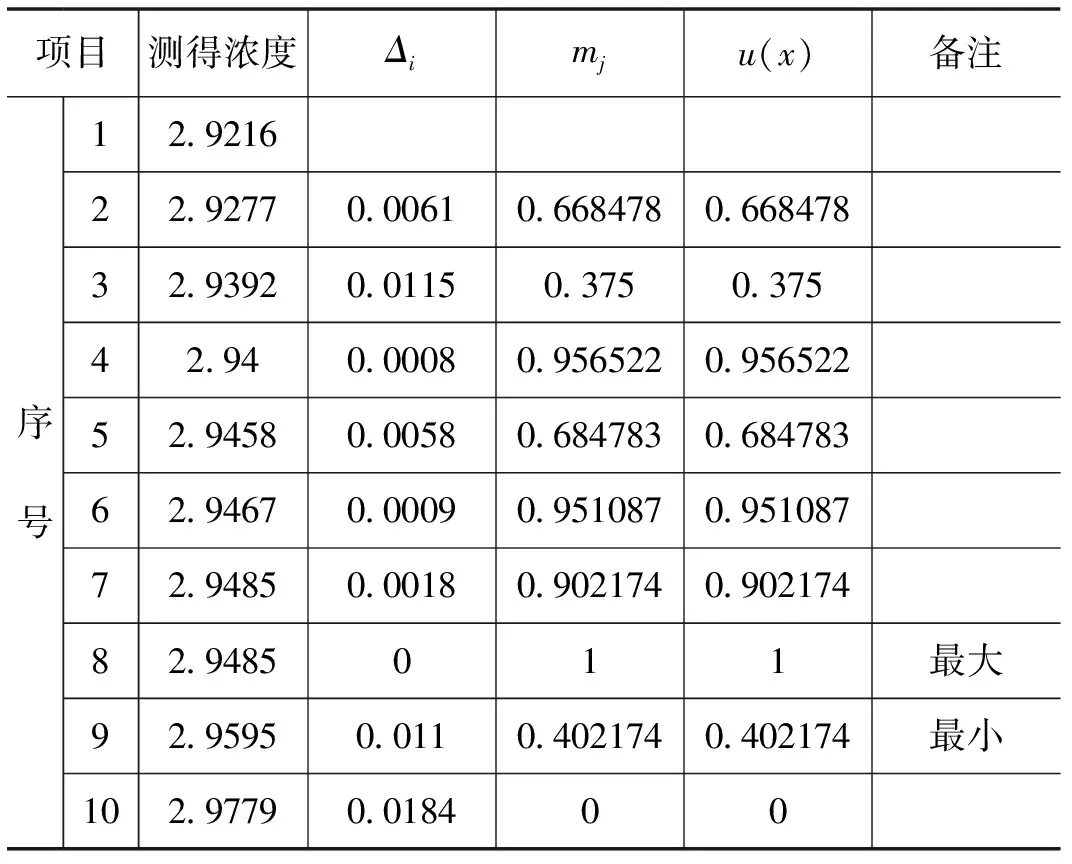
表1　浓度测量线性估计法计算数据

按本文3的要求，使用SUMT优化和罚函数内点法，得结果见表3。

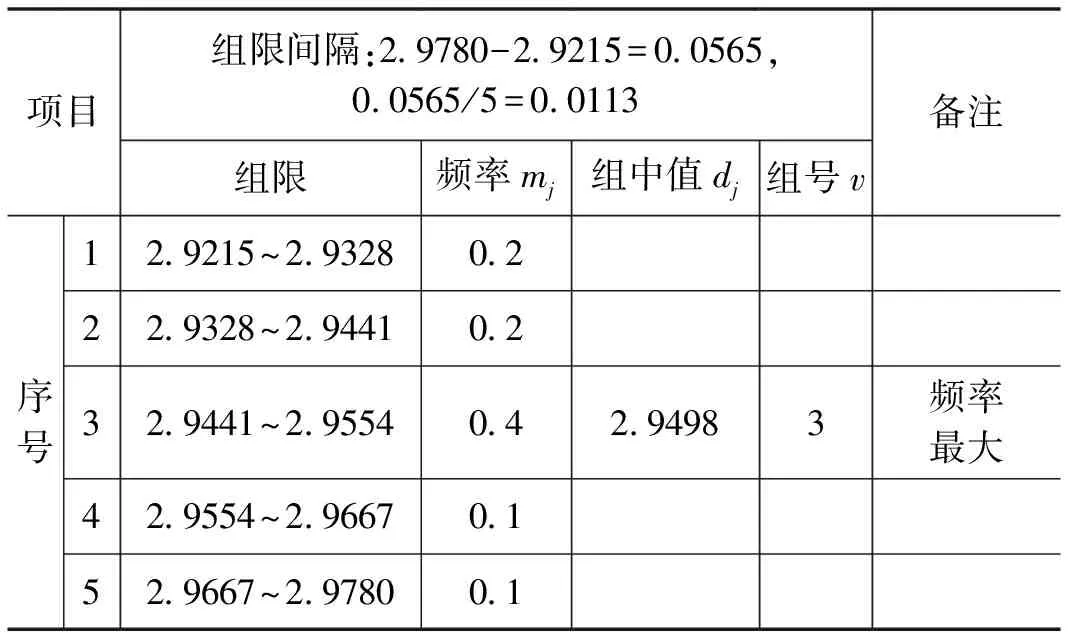
表2　浓度测量直方图法计算数据

由表3，电感耦合等离子体(ICP)发射光谱仪测量铜溶液(浓度在0～3.0000μg·mL-1范围)的扩展不确定度为：

U95=0.0325μg·mL-1

表3　计算结果

7　讨论

用经典的方法来评定测量的扩展不确定度为0.0343μg·mL-1;用本文模糊集合理论来评定的扩展不确定度为0.0325μg·mL-1。其相对误差为(0.0343-0.0325)/0.0343=5.2％。

实验结果表明，测量值服从正态分布，对不确定度的评定误差而言，本文采用的方法与经典方法效果相当。置信水平可达到95％以上。

本文采用的方法适用于不同条件，允许测量值不服从正态分布。采用的线性估计法能根据测量数据的离散特性(离散特性是已知或未知的)自动识别隶属函数μ(x)，从而可以在分布条件未知的情况下得到与真值很接近的结果。

本文采用方法的显著特点是：允许采样个数少。另一特点是：无论测量值的分布如何，可以不必像统计学那样先评定标准差、再设计置信系数、最后得出不确定度值，而是直接求出l*水平下的不确定度。

与目前的许多方法相比较，本文的方法更适合于小样本含量、分布条件未知的情况。

[1]辛仁轩，等.离子体发射光谱分析.北京：化学工业出版社，2005

[2]沈帮兴.工程实验设计.北京：测绘出版社，1990

[3]胡宝清.模糊理论基础.武汉：武汉大学出版社，2004

[4]杨纶标，高英仪.模糊数学原理及应用.广州：华南理工大学出版社，2004

[5]孙靖民，米成秋.机械结构优化设计.哈尔滨：哈尔滨工业大学出版社，1985

[6]卢险峰.最优化方法应用基础.上海：同济大学出版社，2003

[7]俞玉森.数学规划的原理和方法.武汉：华中理工大学出版社，1993

[8]王中宇，夏新涛，朱坚民.测量不确定度的非统计理论.北京：国防工业出版社，2000

[9]王英，杨曙年.电感耦合等离子体发射光谱仪测量不确定度的评定.中国计量，2007(6)