高精度机动车GPS测速仪模拟校准技术研究*

白　银　孙　桥　杜　磊　于　梅　白　杰

(中国计量科学研究院，北京 100029)

0　引言

高精度机动车GPS测速仪由于其测速精度高，对天气环境要求较低，而且安装简便，正在逐渐被计量机构用作对机动车测速仪工作器具进行现场校准的标准器具。由于目前在国内广泛使用的标准器具是光电式非接触测速仪，有研究者将高精度机动车GPS测速仪与其进行比对试验。结果表明，高精度机动车GPS测速仪的测速精度及响应速度、信噪比等性能都能够满足机动车现场测速对标准器的需求[1,2]。因此对其校准技术的研究需求也在逐渐增长。目前国内对于高精度机动车GPS测速仪的研究大多集中在测速方法研究以及标准器具的研制上[3-6]。在GPS信号模拟器的溯源技术研究方面，瑞士国家计量院(METAS)利用标准器具比对的方法来对GPS测速仪模拟器进行校准[7]，我国的研究者对GPS信号模拟器的校准方法也已经有一定研究成果[8]。为此，本文对同一台高精度机动车GPS测速仪，分别使用两种模拟校准系统进行模拟测速误差校准，介绍了高精度机动车GPS测速仪的模拟测速误差校准技术，验证了模拟测速误差校准能够作为高精度机动车GPS测速仪量值溯源的有效途径。

1　高精度机动车GPS测速仪工作原理

GPS导航系统具有全球、全天候、连续、实时的精密三维导航与定位能力。GPS测速仪通过安装在运动载体上的GPS接收器获取GPS信号，从而得到运动载体的运动速度。GPS测速方法可分为单点测速、基于位置差分解算测速、基于速度修正差分测速、基于载波相位中心差分测速和基于原始多普勒频移解算测速。其中，前四种方法的测速准确度不仅与载波相位观测值的准确度有关，而且受到载体运动状态的影响。如果载体不是匀速运动，其速度测量准确度必定受影响，速度变化越大，速度测量误差就越大，所以这四种方法在测速精度要求较高的实际应用中并不多见[9]。

基于原始多普勒频移观测值的解算方法是一种普遍使用的高精度GPS测速方法，基本不受载体运动状态的影响。多普勒频移是观测者接收到的GPS卫星载波频率fr与GPS卫星发射的载波频率fs之间的频率差fd，有：

(1)

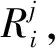
(2)

根据GPS单点定位的数学模型，对站星伪距进行微分后，得到单点测速的数学模型：

(3)

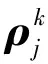
在式(3)中，只有测速仪的三维速度和测速仪钟速4个未知数。理论上，如果能够观测到4颗或4颗以上的卫星，就可以利用最小二乘法求得载体的速度。

2　基于GSS6700的模拟校准系统

2.1　系统构成

Spirent公司生产的GSS6700多功能GNSS模拟器(型号GUSA-0120)具有GPS信号模拟、记录和回放功能，能够使用自行编制的测速模拟程序创建与真实使用环境相近的场景，对高精度机动车GPS测速仪进行校准。本文利用这一功能，结合卫星信号场模拟装置构建的校准系统工作示意图如图1所示[10]，校准系统如图2所示。

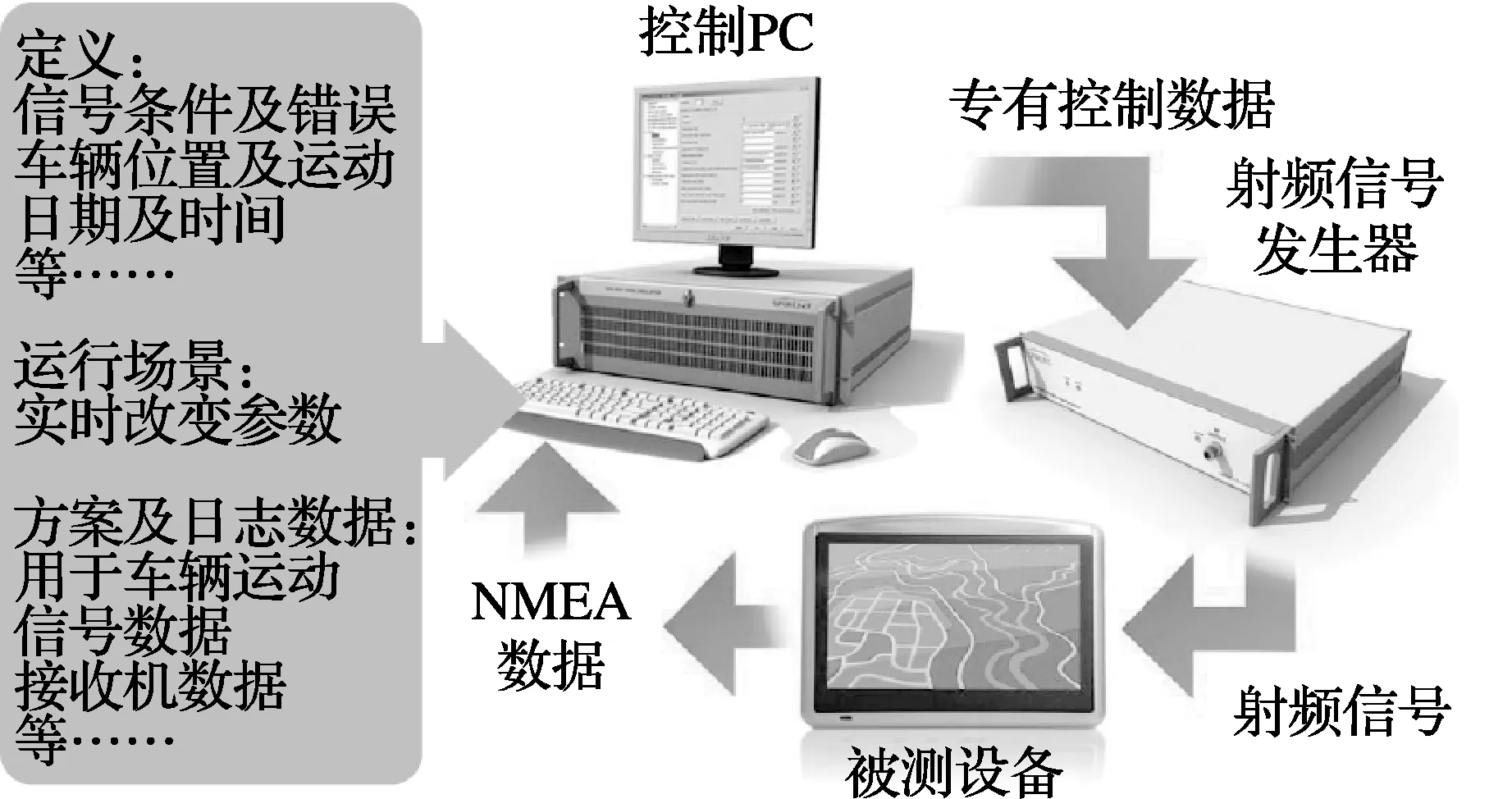
图1　使用GSS6700的模拟校准系统工作示意图

图2　使用GSS6700的模拟校准系统图

2.2　试验与分析

被校高精度机动车GPS测速仪(型号Racelogic VBOX III，刷新率100Hz)在20～200km·h-1范围内的模拟测速误差校准结果如表1所示，模拟校准过程中卫星数量9颗，每个速度点校准400次。为了检验校准装置是否符合机动车测速仪标准器校准的要求，测量误差的计算依照JJF 1193—2008《非接触式汽车速度计校准规范》的规定：不大于50km·h-1时，计算绝对误差，km·h-1；大于50km·h-1时，计算相对误差，％。

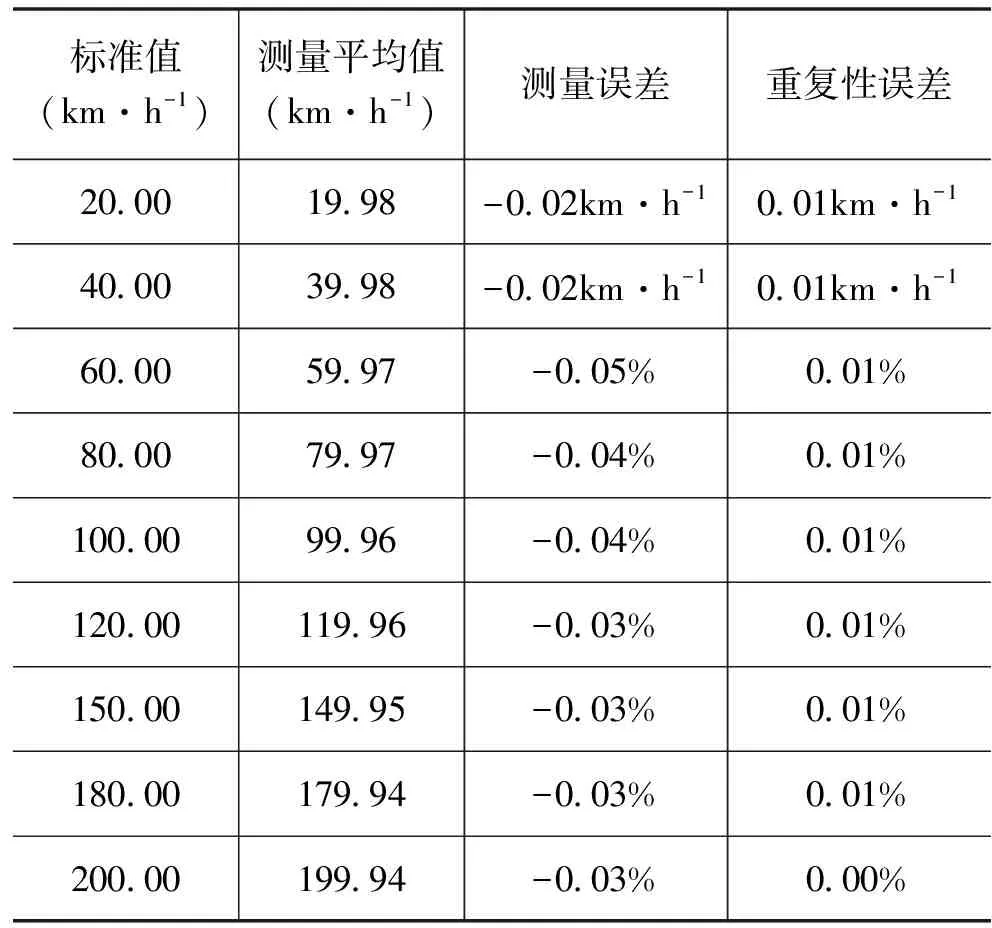
表1　基于GSS6700的模拟校准系统校准结果

从表1中数据可以看出，使用基于GSS6700的模拟校准系统对被校仪器进行校准，各个速度点的模拟测速误差均为负误差，且不大于-0.05km·h-1或-0.05％，相对误差随被测速度增加而降低。各个速度点的重复性误差均不大于0.01km·h-1或0.01％。

2.3　不确定度评估

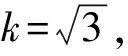
以测量误差及测量重复性误差最大的60km·h-1作为参考速度值，进行不确定度评定。按照输入量的不确定度来源及评定，列出输出量的标准不确定度分量，见表2。

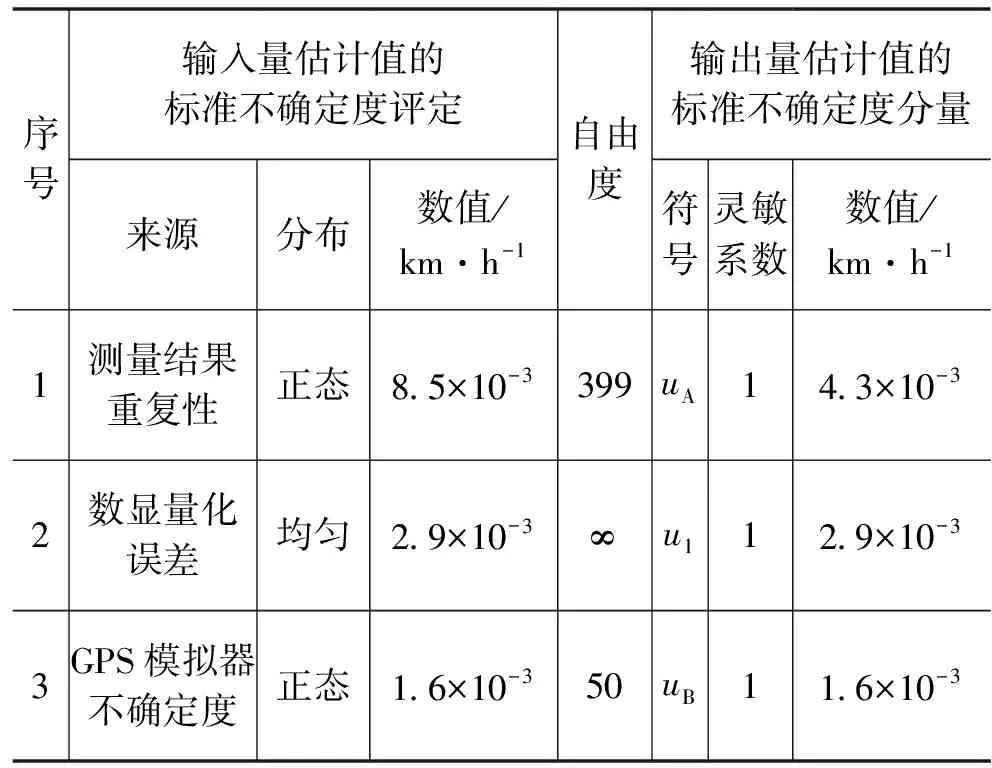
表2　基于GSS6700的模拟校准系统不确定度分量表

由于各标准不确定度分量相互无关，故合成标准不确定度为：

(4)

合成相对标准不确定度为0.011％，故相对扩展不确定度为0.022％，k=2。

3　基于Labsat的模拟校准系统

3.1　系统构成

Racelogic公司生产的LabsatGPS信号模拟器(型号Labsat)同样具有GPS信号模拟、记录和回放功能，工作示意图如图3所示。本文利用Labsat信号模拟器运行自行编制的测速场景模拟程序，结合卫星信号场模拟装置构建的校准系统如图4所示。

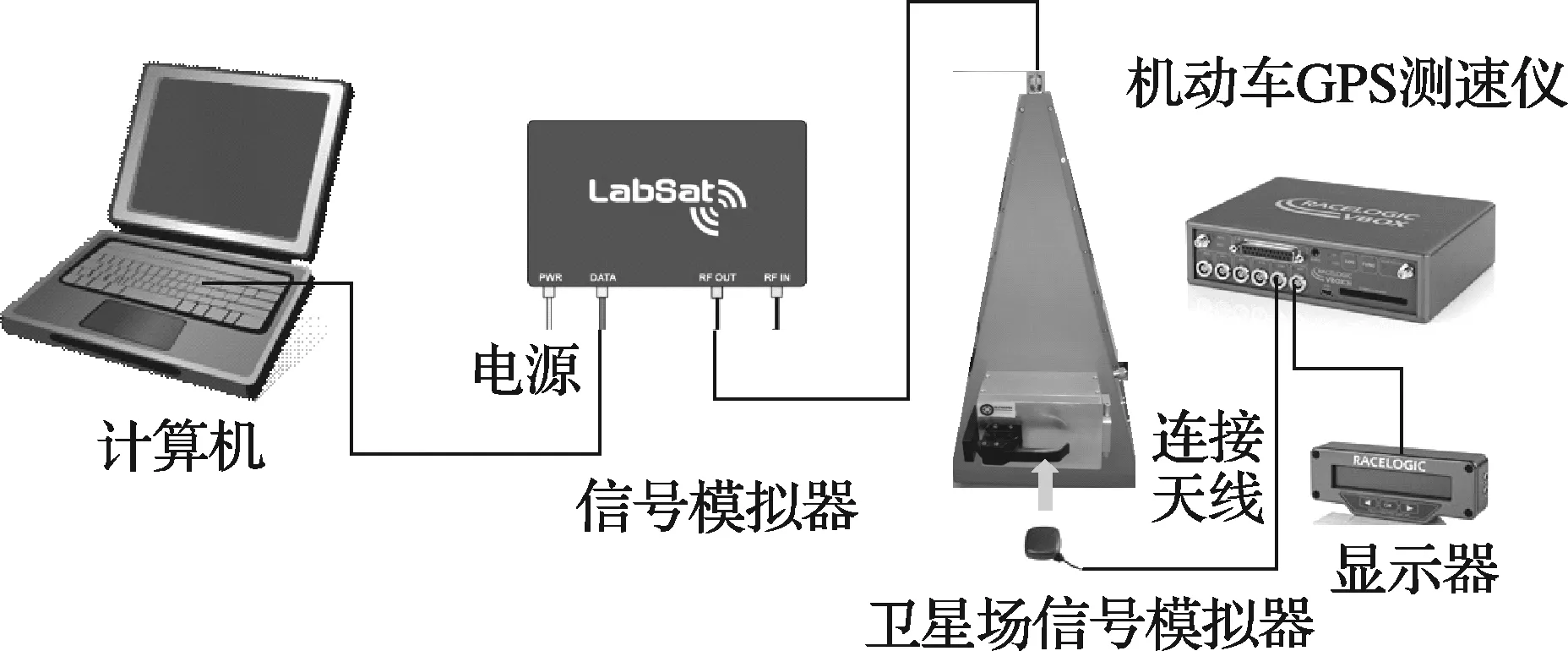
图3　使用Labsat的模拟校准系统工作示意图

图4　使用Labsat的模拟校准系统图

3.2　试验与分析

被校高精度机动车GPS测速仪(型号Racelogic VBOX III，刷新率100Hz)在20～200km·h-1范围内的模拟测速误差校准结果如表3所示，模拟校准过程中卫星数量9颗，每个速度点校准400次。测量误差的计算同表1。

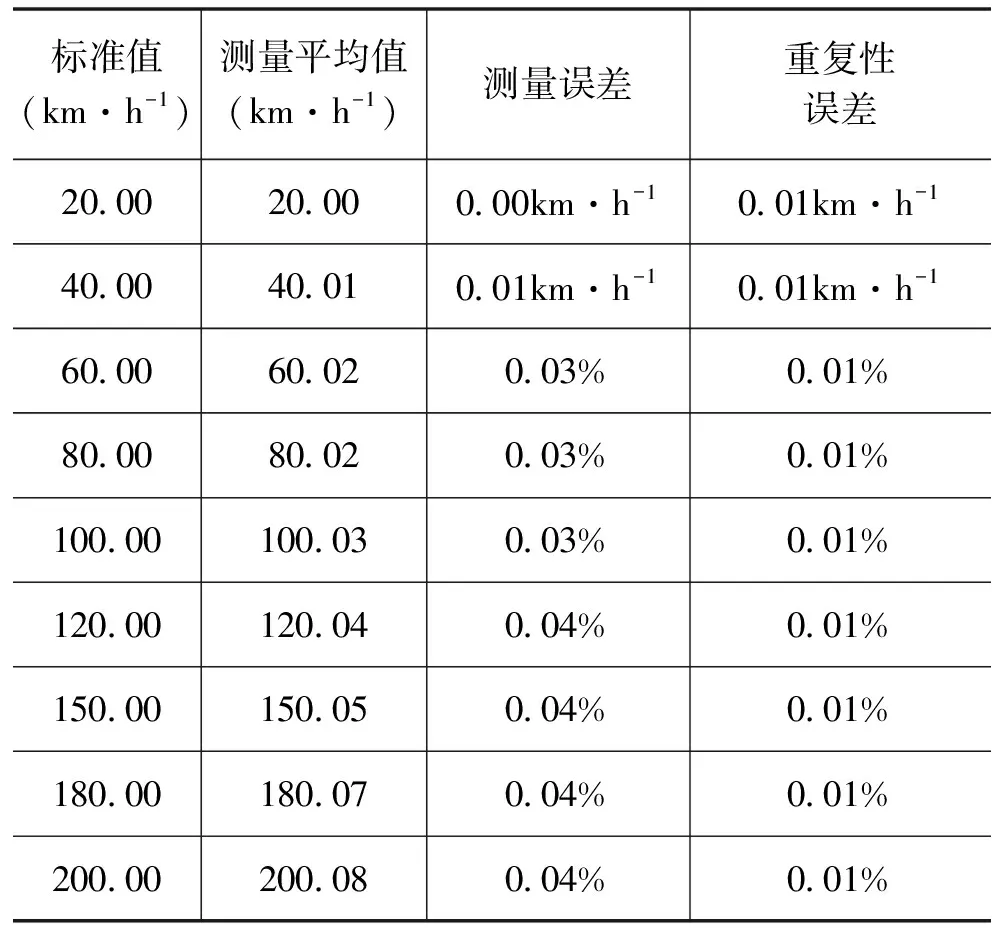
表3　基于Labsat的模拟校准系统校准结果

从表3中数据可以看出，使用基于Labsat的模拟校准系统对被校仪器进行校准，各个速度点的模拟测速误差均为正误差，且小于0.05km·h-1或0.05％，测速误差随被测速度增加而增加。重复性误差均不大于0.01km·h-1或0.01％。

3.3　不确定度评估

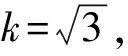
为了更好的与GSS6700模拟校准系统进行比较，以60km·h-1作为参考速度值，进行不确定度评定。按照输入量的不确定度来源及评定，列出输出量的标准不确定度分量，见表4。

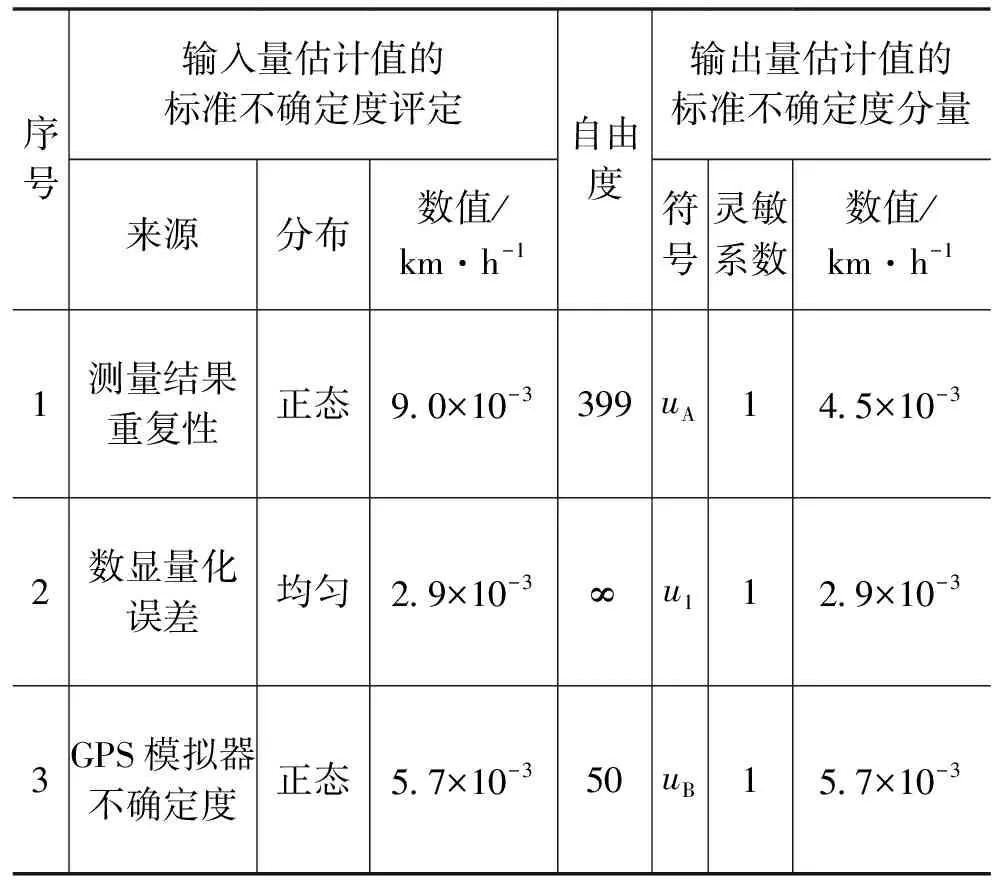
表4　基于Labsat的模拟校准系统不确定度分量表

由于各标准不确定度分量相互无关，故合成标准不确定度为：

(5)

合成相对标准不确定度为0.015％，故相对扩展不确定度为0.030％，k=2。

4　结束语

本文对同一台高精度机动车GPS测速仪分别使用两种模拟校准系统进行了模拟测速误差校准，并进行了不确定度分析：

1)校准结果显示两种模拟校准系统均能够在20～200km·h-1范围内进行有效校准，不同速度点的模拟测速误差均在±0.05km·h-1或±0.05％范围内，校准不确定度分别优于0.024％(k=2)和0.030％(k=2)。

2)上述结果表明，高精度机动车GPS测速仪模拟测速误差校准法的不确定度小于高精度机动车GPS测速仪最大允许误差绝对值(0.1km·h-1)的三分之一[12]，因此能够作为高精度机动车GPS测速仪量值溯源的有效途径。在实验室完成高精度机动车GPS测速仪测速范围和模拟测速误差等关键计量指标的校准项目，避免了繁琐危险的现场实车高速试验，科学合理、溯源明确、可操作性强。经过模拟测速误差校准的高精度机动车GPS测速仪作为机动车测速标准器具使用，具有较大的推广应用前景。

[1]D Summers & S Lewis, HOSDB.Guidance for test houses on the use of satellite speed measurement equipment for Home Office type approval tests.2006

[2]Certificate of calibration No.258-14815, Federal Office of Metrology METAS, 3003 Bern-Wabern, 27.September 2011

[3]赵军, 刘美生, 杨春生, 等.基于 GPS 技术的速度标准装置研究[J].微计算机信息, 2008, 24(25): 245-246

[4]靳力.基于高速GPS的道路测速设备计量校准系统[J].计算机光盘软件与应用, 2013 (4): 180-182

[5]张宝峰, 耿丽红.GPS 单点测速误差分析与数据处理[J].天津理工大学学报, 2010, 26(003): 13-15

[6]戚淑芬, 李明, 李利洁, 等.嵌入式 GPS 数据采集系统的设计与实现 [J].仪器仪表学报, 2006, 27(1): 127-129

[7]A Comparison of non-contact speed sensors [EB/OL].Racelogic Corporation.http://www.racelogic.co.uk/_downloads/vbox/Application_Notes/Comparison％20of％20Non-contact％20Speed％20Sensors.pdf

[8]陈海咏, 金雷鸣.GPS 信号仿真器校准方法[J].上海计量测试, 2011, 224(4): 13-15

[9]叶芳.基于GPS 技术的车速传感器的研制与应用[D].重庆大学, 2009

[10]GPS/AGPS及Spirent_GSS6700模拟信号发生器介绍[CP/OL], Wistron Corporation, 2001.[2001-8-2].wenku.baidu.com/view/22d9f488d4d8d15abe234ee6.html?

[11]C Elster, A Link.Analysis of key comparison data: assessment of current methods for determining a reference value [J].Meas Sci Technol.2001, 12 (9):1431-1438

[12]JJF 1094—2002 测量仪器特性评定技术规范