移动荷载作用下沥青路面结构时程响应分析①

蒋建国，何金龙，梁洪涛

(中南大学土木工程学院，湖南长沙410075)

随着交通运输业的迅速发展，车辆重载交通和超载运输现象越来越严重，造成很多路面出现各种形式的破坏，如沉陷、开裂和车辙等病害，使路面的使用寿命大大缩短，车辆与道路相互作用的研究越来越受到工程界和学术界的重视［1］。行驶的车辆对路面产生的是移动荷载，这种荷载不仅作用位置在变化，荷载大小也是不停变化的，车辆简谐荷载可以很好的模拟行车荷载大小的变化，而沥青路面是半无限空间上的多层体系结构，采用三维模型，可以对路面结构在移动荷载作用下任意点位的动力响应进行研究，更符合路面的实际受力特性［2］。因此，基于上述描述，本文利用有限元分析软件ANSYS软件建立三维有限元计算模型，分析竖向移动荷载作用下沥青路面动态响应(动位移、动应力和动应变)的变化趋势，并比较车速变化对各力学指标的影响，以期能对沥青路面设计和施工养护提供一些参考。

1 车辆荷载模型的选取

汽车在道路上行驶，由于路面状况(路面不平整度)的不同，导致车辆响应不同，使路面所承受的车辆荷载具有随机性［3］。

简谐振动模型是路面动力学分析中一种有效的方法，简谐振动模型以振动的振幅、频率及周期性来描述其特征，这种方法既能简化计算，也可以较好的体现车辆动荷载的动力特性。

本文采用一系列幅值不等的正弦波荷载作为车辆动载和路面结构动力响应分析的前提，其表达式为:

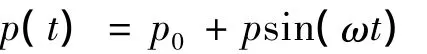
式中:p0为车辆静载;p为车辆动载振动幅值，p= M0aω2;M0是车辆模型簧下质量;a是几何不平顺矢高，反映了路况，a=2 mm(国际高速公路平整度指数);ω为振动圆频率，ω=2πν/L;ν为车辆的运行速度;L为路面几何曲线波长，取车身长，即为6 m。

经调查，两轴车是高速公路上所占比例最大的车型，属于典型重型车辆，可以以该车型为典型车辆分析其对路面的动荷载［4］。本文车型采用两轴六轮的“东风”重型普通货车，后轴为双轮，外轮距2.05 m，内轮距1.60 m，前轴轮距1.90 m，前轴与后轴的轴距为5.90 m。该型车辆空车重120 kN，满载时荷载总重300 kN。车辆满载时的轴载分配参数见表1。

表1 满载时的装载重量和轴载分配Table 1 Load weight and axle load distribution of full load

加载时考虑轮胎接地面积，当车辆满载时，荷载作用面积为0.33 m×0.464 m。

2 有限元计算模型的建立

本文计算模型选取半刚性基层沥青路面结构，并采用弹性层状体系理论分析路面结构在荷载作用下的应力应变及位移。弹性层状体系模型假设条件如下［5］:(1)各层材料都是连续的、均匀的和各向同性的，位移和变形是微小的，且每一层各个位置的材料性能与结构厚度均相同;(2)最下一层水平方向和厚度都是无限的，上面的各层具有有限的厚度，水平方向无限延伸;(3)层间接触条件，也就是应力和位移等满足连续条件;(4)最下层无限深处和其上各层的无限远处，其应力应变和位移均为0。

路面结构具体材料参数如表2所示，运用ANSYS建立路面结构三维实体模型，三维模型长(x方向)16.5 m、宽(y方向)6 m、高(z方向)6 m，如图1所示。道路纵向两个断面的x方向位移被约束，道路横向两断面y方向位移被约束，底面全部约束，路面边界为完全自由边界。

表2 路基路面结构有限元计算参数Table 2 Parameters in calculation of finite element of subgrade and pavement

如图1所示，对边界1，2和3设置为黏弹性人工边界。该边界可以模拟边界外半无限介质的弹性恢复性能，具有较好的频率稳定性且应用方便，在ANSYS中可以得到实现，且经过验证能够满足精度要求［6］。

根据车辆荷载模型特点，路面中心线为荷载接触中心线。为减少边界效应的影响，行车起点在x =5.775 m处，行车终点在x=10.725 m处。车辆荷载采用经随机荷载转化后的正弦波荷载，采用阶跃加载的方式来模拟移动荷载。有限元模型在荷载加载区域范围内细分，满足荷载加载面积及移动规律。加载时，首先在起点选择一组单元，单元个数为2×2，如图2所示，在其上施加面荷载F1，持续时间为0.008 25 s;然后删除面荷载F1，轮载向前移动一排单元，构成另外一组加载单元，并在其上施加面荷载F2，持续时间不变，依次类推，直至选择最后一组单元，并施加最后一个轮载F27，循环结束，这样就相当于车辆以20 m/s的速度向前行驶。采用不同车速时，只要改变载荷在每组单元上的持续时间即可。

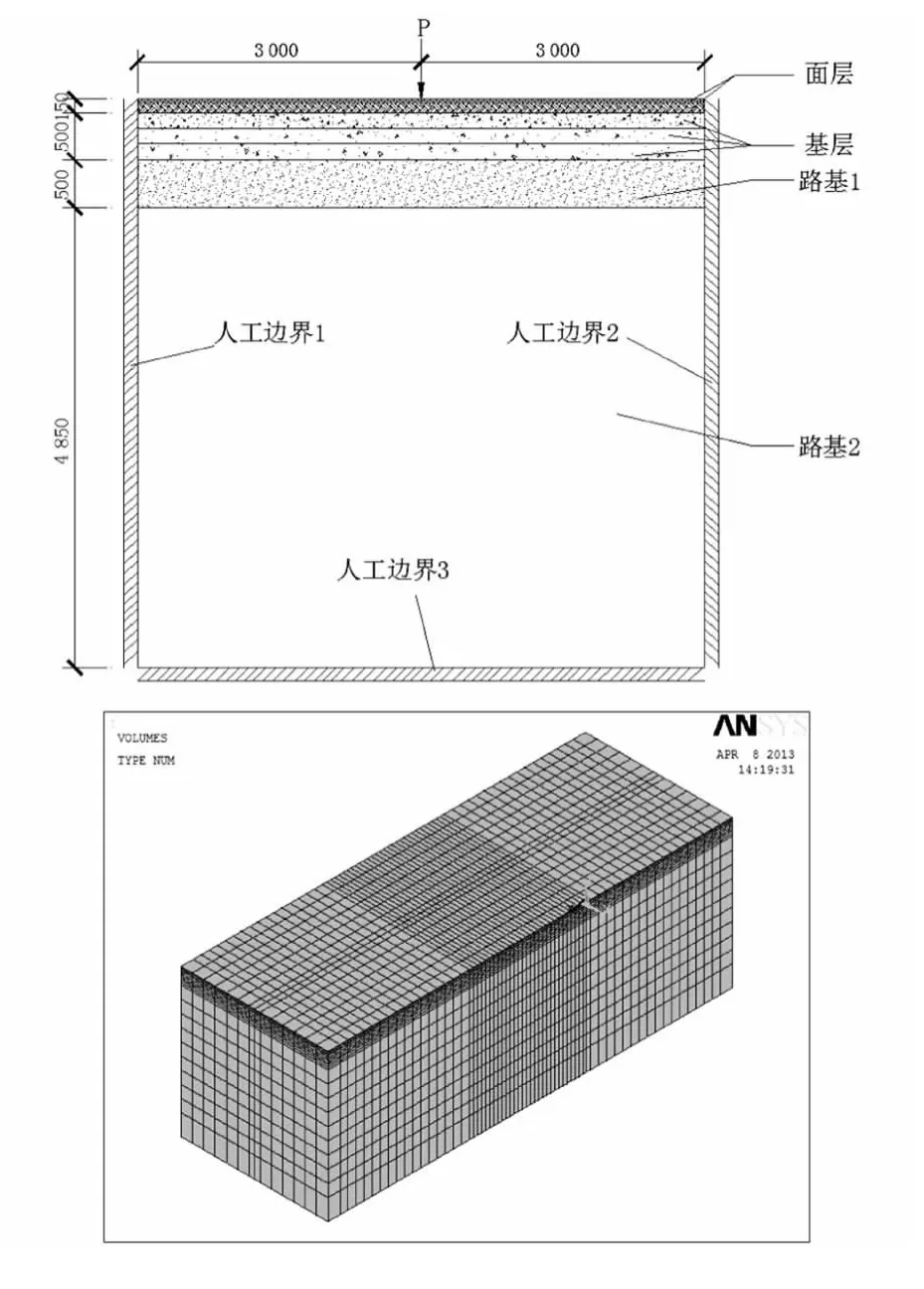
图1 路面结构计算模型Fig.1 Calculationmodel of pavement structure

图2 加载单元示意图Fig.2 Loading unit

有限元计算分析求解采用ANSYS软件中的Full法［7］，并用瞬态求解器进行动力方程的求解，以下分析均取车辆满载情况下以20 m/s的车速行驶时的路面动态响应求解结果，选取的计算点位为各层接触面(包括面层表面)的中心点。

3 沥青路面结构时程响应分析

3.1 竖向位移时程响应分析

竖向位移(弯沉)是沥青路面设计中一个重要的力学指标［8］，弯沉过大，路面各层就容易发生破坏，它直接反映了路面强度的好坏。由图3可知:沥青表面层的竖向位移最大，竖向位移随着路面深度的增加而逐渐减小，各层间位移的最大差值均出现在加载点，随着与加载点距离的增加，各层竖向位移的差值也在逐渐减小。

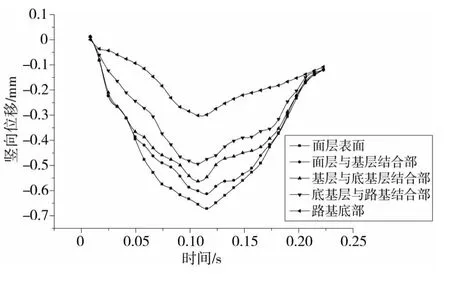
图3 竖向位移的时程曲线Fig.3 Time－history curve of vertical displacement

3.2 应力时程响应分析

3.2.1 竖向应力时程响应分析

由图4可以看出:竖向应力主要是压应力，随着深度的增加而逐渐减小，且深度越小，衰减速率越快，到达路基底部时，竖向应力已经接近为0。由此表明，沥青路面面层很容易受到挤压变形，因此在进行路面铺筑时，一定要对沥青面层进行充分压实，以免由于进一步的车辆荷载而造成车辙。

图4 竖向应力的时程曲线Fig.4 Time－history curve of vertical stress

3.2.2 水平应力时程响应分析

由图5可以看出:路面各层的水平应力均呈交替变换状态，其中最大压应力出现在沥青面层的表面，随着深度的增加压应力渐渐变小，至基层与底基层结合部位时，水平应力变为拉应力，并随着深度增加拉应力逐渐变大，最大拉应力出现在底基层与路基结合部。面层也会出现拉应力，但是拉应力极小，对路面的影响不大，面层以下各层也有压应力，同样压应力也很小，可以忽略不计。至路基底部时，水平应力已基本接近为0。通过以上分析，再次说明路面压实的重要性，应避免水平压实度不足而因为外部荷载使路面发生凹陷;同时说明，面层以下的各层之间很容易因为超过极限拉应力而造成各结合部位的开裂，因此，采取必要措施防止开裂，阻止开裂部位向上层扩散，就可以有效解决在沥青面层形成反射裂缝而造成的路面结构破坏。

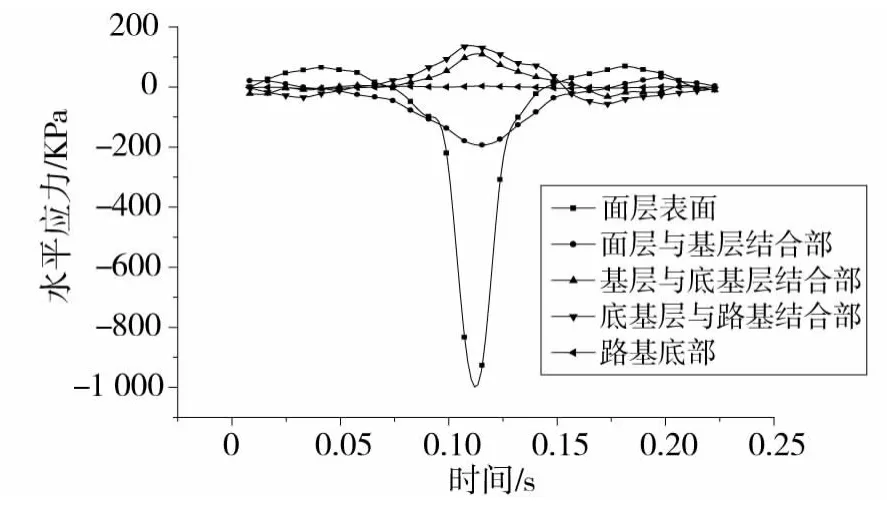
图5 水平应力的时程曲线Fig.5 Time－history curve of horizontal stress

3.2.3 横向应力时程响应分析

由图6可以看出:路面各层的横向应力自上而下先承受压应力再承受拉应力，在基层与底基层结合部位由压应力转变为拉应力，最大横向压应力出现在沥青面层表面，最大横向拉应力出现在底基层与路基结合部，到路基底部时水平应力的影响已经很不明显。通过对比每一结构层水平应力和横向应力的幅值，横向应力和水平应力均相差不大，所以在考虑路面破坏时，横向应力的影响也要考虑在内。

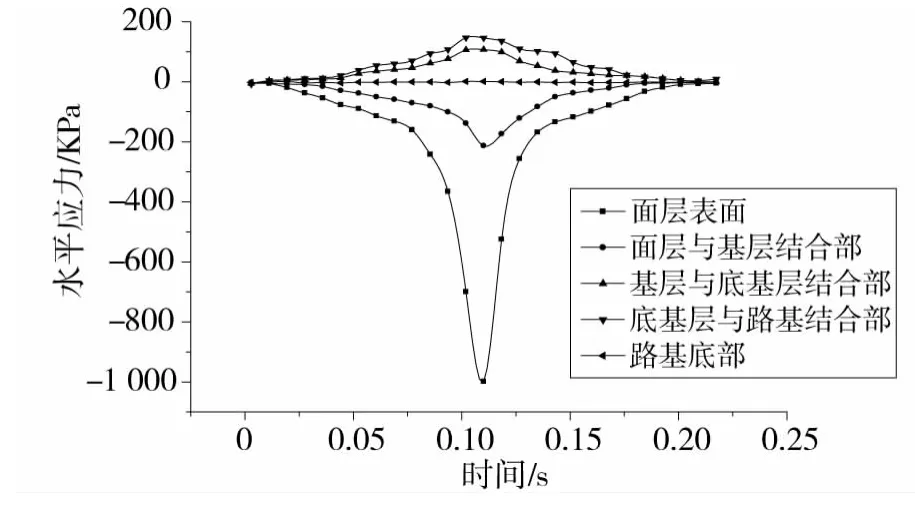
图6 横向应力的时程曲线Fig.6 Time－history curve of transverse stress

3.2.4 水平剪应力时程响应分析

由图7可以看出:路面各结构层的水平剪应力是正负交替变化的，在面层范围内水平剪应力随着深度的增加而增大，到面层与基层结合部时双向水平剪应力均达到最大值，随后水平剪应力开始随着深度的增加而逐渐变小，至路基底部时，水平剪应力已经可以忽略不计。因此在选择面层材料时必须充分考虑到材料的抗剪切强度及抗剪切疲劳能力。

图7 水平剪应力的时程曲线Fig.7 Time－history curve of horizontal shear stress

3.3 应变时程响应分析

3.3.1 竖向应变时程响应分析

由图8可以看出:竖向应变在沥青路面的面层呈现出拉压应变交替变换的状态，当车辆接近和远离计算点位时承受拉应变，车辆作用在计算点位上时承受压应变，路面面层在这种持续的拉压应变作用下，很容易出现滑移而与基层脱离。以下各层均为压应变，压应变使各结构层产生向下的弯沉，当弯沉超过了结构层所能承受的极限值时，就会使路面结构发生断裂。

图8 竖向应变的时程曲线Fig.8 Time－history curve of vertical strain

3.3.2 水平应变时程响应分析

由图9可以看出:路面各层的水平应变均呈交替变换状态，既有拉应变也有压应变，最大压应变出现在沥青面层表面，最大拉应变出现在底基层与路基结合部。压应变和拉应变的交互作用很容易使各结构层在水平方向出现裂缝，当裂缝过大时就会导致结构层发生开裂，从而使路面结构破坏。

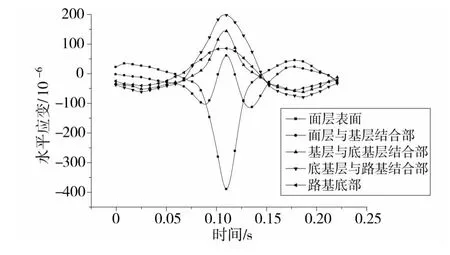
图9 水平应变的时程曲线Fig.9 Time－history curve of horizontal strain

3.3.3 横向应变时程响应分析

由图10可以看出:沥青面层表面主要承受压应变，其余各层均承受拉应变，最大拉应变出现在底基层与路基结合部。和水平动应变的破坏作用一样，主要是造成各结构层的拉裂破坏。

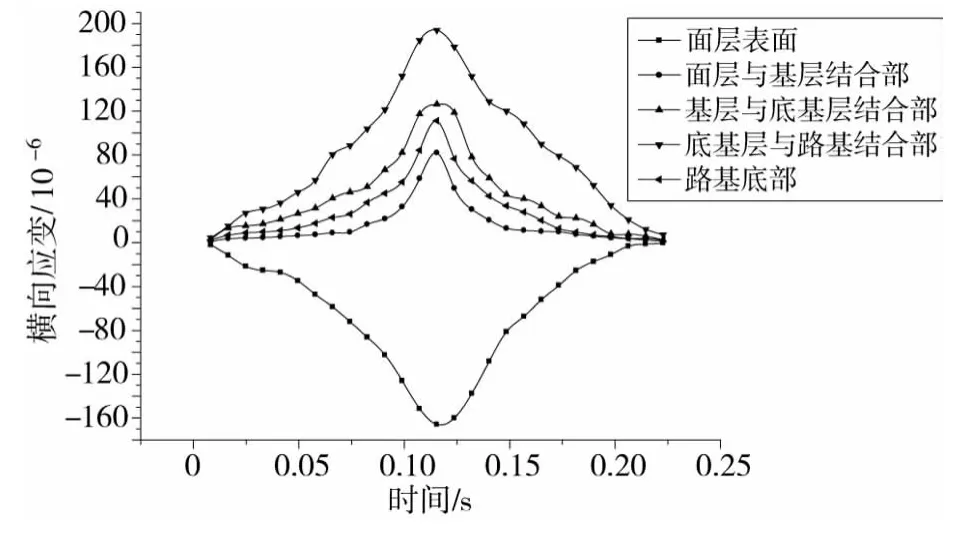
图10 横向应变的时程曲线Fig.10 Time－history curve of transverse strain

4 车速对动力响应的影响

选定面层表面的最大竖向位移和最大竖向压应力、面层底部最大水平剪应力以及底基层底部的最大水平拉应变作为代表值进行分析。

由图11～14可知:各力学响应指标的大小并不是单纯随着车辆行驶速度的增加而增加或者减小，而是存在一个使动力响应规律发生变化的拐点速度，竖向位移、竖向应力和水平应变的拐点速度大致为20 m/s，而水平剪应力的拐点速度在15 m/s左右。在车速较小的时候，各力学指标随车速增加的减小幅值较大，基本上呈现出线性变化;当超过拐点速度后各力学指标随着车速的增加而增大，竖向位移尤为明显，但应力和应变的增加幅值较小，并且到了一定速度之后，应力和应变开始趋于稳定。

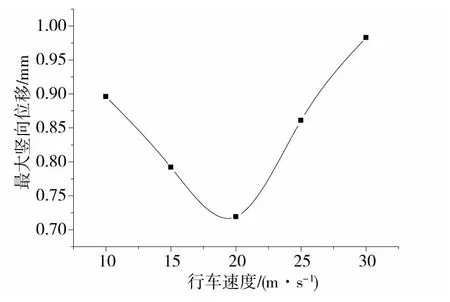
图11 面层表面最大竖向位移Fig.11 Maximum vertical displacement of the surface of surface course

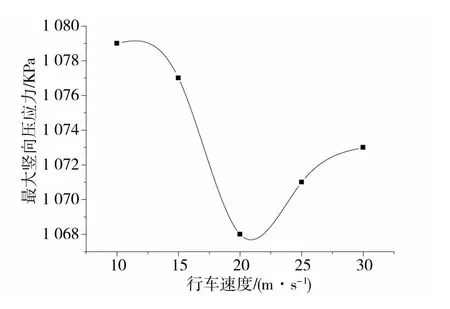
图12 面层表面最大竖向压应力Fig.12 Maximum vertical compressive stress of the surface of surface course

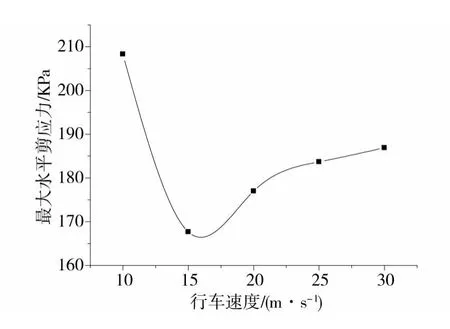
图13 面层底部最大水平剪应力Fig.13 Maximum horizontal shear stress of the bottom of surface course

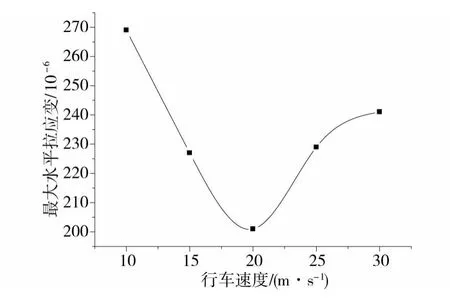
图14 底基层底部最大水平拉应变Fig.14 Maximum horizontal tensile strain of the bottom of subbase

5 结论

(1)最大位移出现在轮载作用点下方，离轮载作用点越远，竖向位移越小;沥青面层结构主要处于3向受压状态，基层和底基层一般处于受拉状态;水平剪应力的最大值出现在面层与基层结合部，随后随着深度的增加逐渐变小。

(2)车速对路面动力响应存在影响。总体来说是在车速较低时随着车速的增加而减小，当达到某一车速后，随着车速的增加而变大并逐渐趋于稳定。

(3)随机荷载作用下的路面动力响应更符合实际，而路面不平整度是诱发车辆振动的主要激励因素之一。为了减小车辆动荷载对路面的破坏作用，应该严格控制各个施工环节的质量，使路基路面具有良好的压实度和平整度。

［1］王玉.公路工程质量通病防治指南［M］.北京:人民交通出版社，2002:173－209.

WANG Yu.The prevention measures for quality common diseases of road projects［M］.Beijing:China Communications Press，2002:173－209.

［2］王晅.随机荷载作用下柔性路面结构及路基动力响应研究［D］.长沙:中南大学，2006.

WANG Xuan.Study on the dynamic response of flexible pavement structure and subgrade under random load［D］.Changsha:Central South University，2006.

［3］蒋建国，马国存，梁洪涛.随机动载作用下沥青路面的动力响应分析［J］.湘潭大学自然科学学报，2010，32 (4):53－57.

JIANG Jianguo，MA Guocun，LIANG Hongtao.Dynamic response of pavement under the random load caused by pavement roughness［J］.Natural Science Journal of Xiangtan University，2010，32(4):53－57.

［4］吕彭民，董忠红.车辆－沥青路面系统力学分析［M］.北京:人民交通出版社，2010:18－25.

LV Pengmin，DONG Zhonghong.Mechanical analysis of vehicle－asphalt pavement system［M］.Beijing:China Communications Press，2010:18－25.

［5］邓学钧.路基路面工程［M］.3版.北京:人民交通出版社，2008:377－389.

DENG Xuejun.Road subgrade and pavement engineering［M］.3th ed.Beijing:China Communications Press，2008:377－389.

［6］赵健，李振存.汽车荷载作用下沥青路面公路动力响应数值模拟［J］.铁道科学与工程学报，2012，9(5):83－89.

ZHAO Jian，LI Zhencun.Numerical analysis of bitumen－surface highway dynamic response under vehicle loads［J］.Journal of Railway Science and Engineering，2012，9(5):83－89.

［7］梁洪涛.移动荷载作用下层状沥青路面结构时程响应分析［D］.长沙:中南大学，2013.

LIANG Hongtao.Analysis of time－history responses of layered asphalt pavement structure under moving load［D］.Changsha:Central South University，2013.

［8］JTG D500－2006，公路沥青路面设计规范［S］.

JTG D500－2006，Specifications for design of highway asphalt pavement［S］.