斜交高墩大跨度连续箱梁桥动力特性及其颤振分析①

胡立华，李德建

(中南大学土木工程学院，湖南长沙410075)

风对结构的振动反应分为发散振动和限幅振动，颤振和驰振属于发散振动，涡激振和抖振属于限幅振动。发散振动具有危险性，是一种急性病，大跨度桥梁在施工中结构刚度小，容易在短时间内受风致振动影响，因此必须对施工阶段颤振稳定性进行研究，大跨度桥梁的抗风性能首先取决于其动力特性［1］。因此，必须根据悬臂施工的刚度对结构的动力性能作出评价和分析，以保证施工的顺利进行。以酉水大桥(80+145+80)m斜交高墩大跨预应力混凝土连续箱梁桥为工程背景，对最高桥墩施工阶段、最大悬臂施工阶段、成桥阶段3个阶段的动力特性进行分析，依此分析施工阶段的颤振稳定性，得出一些结论。

1 结构动力特性分析方法

1.1 结构动力特性有限元分析

利用Midas－civil对桥梁的动力特性进行分析。结构动力特性主要与结构的质量分布和刚度特性(即模型的边界条件、材料的弹性模量和截面的几何特性)有关，故必须精确模拟分析桥梁结构的质量和刚度特性。在成桥阶段，桥梁铺装等二期恒载也必须转化为均布质量分布于主梁单元。酉水大桥动力有限元模型，在软件Midas－civil中采用空间梁单元模拟，每个节点6个自由度，对应3个线自由度和3个角自由度，同时考虑梁的剪切变形。

结构的动力方程为:

式中:［M］，［C］和［K］分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;{¯δ}，{¯δ}和{δ}分别为结构的加速度、速度和位移向量;{F}为作用在桥梁空间梁单元上的力向量。

求结构自振特性时，一般不考虑阻尼的影响。令［C］=0，{F}=0，则得到其无阻尼自振方程为:

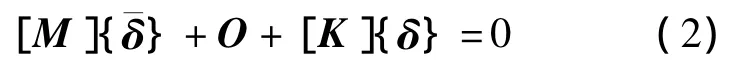
式(2)具有非零解，则:

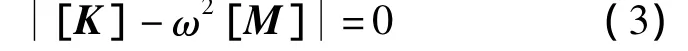
即式(3)的特征方程为:

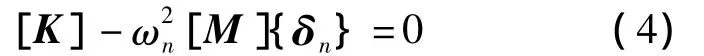
对于式(4)特征值的求解方法较多，常有的有多重Ritz向量法、Lanczos向量迭代法、子空间迭代法、Rayleigh－Ritz法和逆迭代法。从结构分析的角度来说，并不是对所有振型和频率都考虑，一般只需求出较低的几阶即可，这样不仅节省振型存储空间，而且缩短计算时间。本文特征值的求解采用子空间迭代法进行，这种方法能充分利用［M］和［K］2个矩阵的稀疏带状性质，从而提高求解效率。经验表明，子空间迭代法是目前求解大型结构自振频率和振型的最有效方法之一［2－3］。

本文使用子空间迭代法计算桥梁结构前10阶频率和振型，并给出前5阶频率和振型［4］。分析控制最大迭代次数设为20，迭代收敛误差设定为le－10。

1.2 结构动力特性现场测试

为对比结构动力特性有限元分析方法的正确性，同时对结构的动力特性进行现场测试。试验采用由拾振器(位移、速度和加速度传感器)、数据采集仪、电荷放大器及动力分析仪组成的动力测试系统［5］，本结构动力性能现场试验采用德国生产的国际公认的 HBM动力测试与分析系统完成。HBM动力测试与分析系统如图1所示。

图1 振动测试、分析示意图Fig.1 Vibration test and analysis diagram

当桥跨结构无车辆通过时，记录结构在环境随机激励下的加速度响应，通过频谱分析可获得结构的自振特性。

2 酉水大桥斜交高墩大跨度连续箱梁桥动力特性分析

2.1 工程概况

酉水大桥主桥为一座斜交高墩大跨度悬臂浇筑预应力混凝土连续箱梁桥，跨径布置为80 m+ 145 m+80 m。主墩为5号和6号墩，墩身采用双肢矩形空心墩，顺水流布置，主桥墩轴线与桥梁中心线成65°夹角。其中，5号墩高61 m，在墩底往上20 m处设置一个变截面段，横向放坡40∶1，纵向放坡80∶1，20 m以上部分为等截面，空心墩壁厚125 cm。桥梁布置如图2所示。

图2 斜交高墩构造图Fig.2 High skew pier structure

2.2 各施工阶段结构自振测试

为进行斜交高墩大跨度连续箱梁桥在最高墩施工阶段、最大悬臂施工阶段及成桥阶段的动力特性研究，在桥梁边跨跨中以及墩身横向、纵向设置加速度计测试桥梁竖向、横向、纵向在动力激振作用下的加速度值，加速度布置及编号如图3和图4所示。

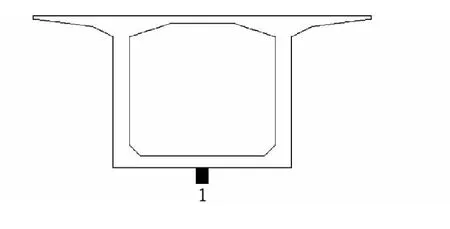
图3 边跨跨中截面加速度传感器布置图Fig.3 Side span midspan section acceleration sensor layout

图4 桥梁5号桥墩截面加速度传感器布置图ig.4 Section of the bridge No5 pier acceleration sensor layout

通过HBM动态数据测试仪采集各施工阶段结构各方向脉动加速度波，应用HBM动态数据分析仪分析各结构加速度频谱，从而得到各测试点方向的结构自振频率。

2.3 最高墩施工阶段结构动力特性

通过Midas－Civil有限元分析软件建立5号墩最高墩模型，将自重荷载转化为质量，计算最高墩阶段动力特性，给出前5阶计算结果如表1和图5所示。

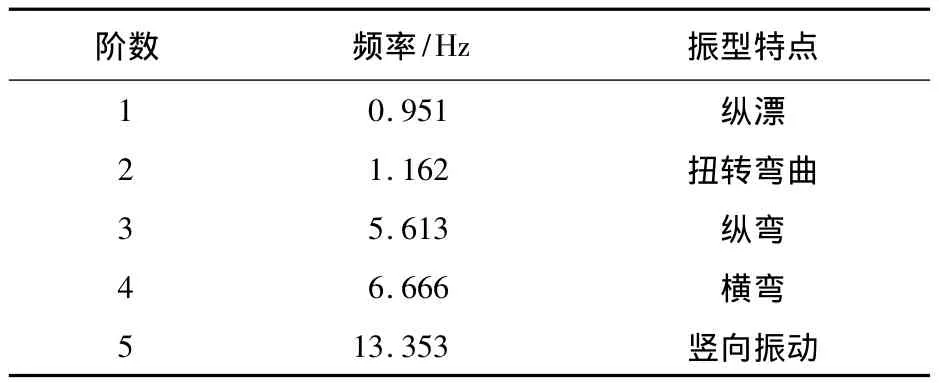
表1 最高墩动力特性计算结果Table 1 Dynamic characteristic calculation results of themaximum pier

从表1可知，在最高墩施工阶段，桥墩动力特性主要表现为桥墩纵漂。

通过HBM动态数据采集仪，在最高桥墩阶段，测点2和3的实测加速度脉动波型如图5所示。

图5 最高桥墩各测点加速度频谱Fig.5 Maximum pier acceleration spectrum of each measuring point

最高墩阶段结构振动频率测试结果与理论计算值对比如表2所示。

表2 最高墩阶段振动测试频率与理论频率比较Table 2 Vibration test frequency and theoretical frequency comparison of themaximum pier

实测桥墩横向、纵向一阶自振频率均比理论计算值大，说明最高墩横向、竖向刚度良好。

2.4 最大悬臂阶段动力特性分析

同理，通过Midas－Civil有限元分析软件建立5号墩最大悬臂模型，将自重荷载转化为质量，计算最大悬臂阶段动力特性，给出前5阶计算结果如表3和图6所示。

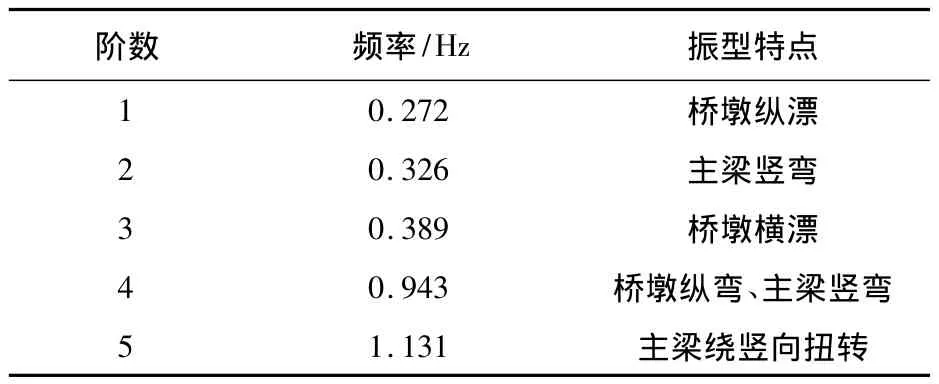
表3 最大悬臂阶段动力特性计算结果Table 3 Dynamic characteristic calculation results of the largest cantilever

从表3可知，在最大悬臂施工阶段，桥梁T构的动力特性主要表现为桥墩纵漂。

通过HBM动态数据采集仪，在最大悬臂施工阶段，测点1，2和3的实测加速度脉动波型如图6所示。

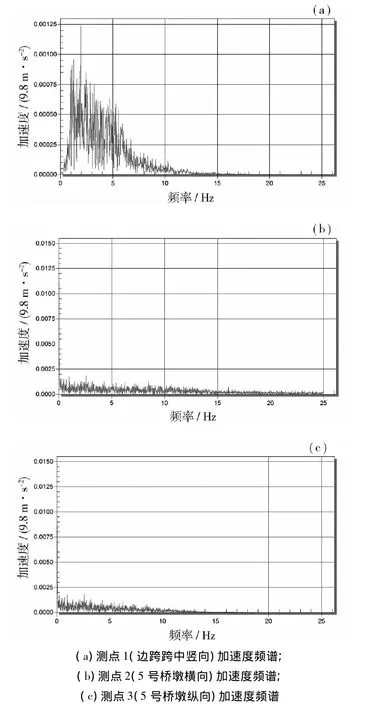
图6 最大悬臂阶段各测点加速度频谱Fig.6 The largest cantilever acceleration spectrum of each measuring point

最大悬臂阶段结构振动频率测试结果与理论计算值对比见表4。

表4 最大悬臂阶段振动测试频率与理论频率比较Table 4 Vibration test frequency and theoretical frequency comparison of the largest cantilever

从表4可知，最大悬臂结构3测点实测结构频率比理论计算值大，说明最大悬臂阶段结构横向、纵向竖向刚度良好。

2.5 成桥阶段结构动力特性分析

同理，通过Midas－Civil有限元分析软件建立酉水大桥成桥模型，主桥左边引桥连接，右边与桥台连接，将二期恒载转化为质量，计算酉水大桥成桥阶段动力特性，给出前5阶计算结果如表5和图7所示。

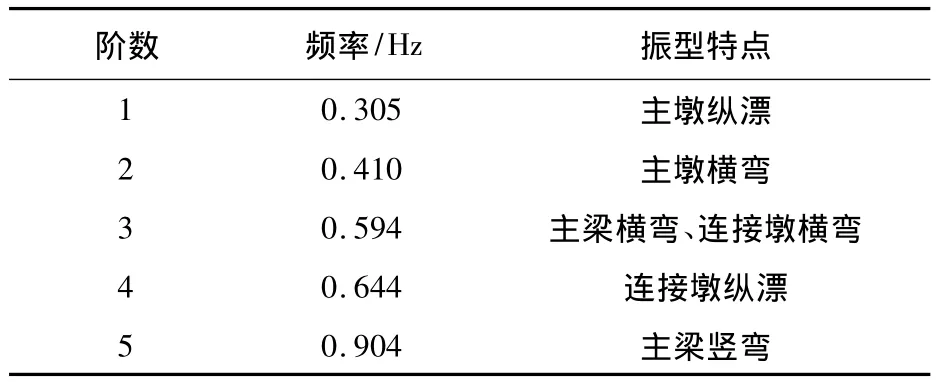
表5 成桥阶段动力特性计算结果Table 5 Dynamic characteristic calculation results of the bridge

由表5可知，在成桥阶段，桥梁结构动力特性主要表现为桥墩纵漂。

同理，在成桥阶段，通过HBM动态数据采集仪，在最大悬臂施工阶段，测点1，2和3的实测加速度脉动波型如图7所示。

成桥阶段结构振动频率测试结果与理论计算值对比见表6。

表6 成桥阶段振动测试频率与理论频率比较Table 6 Vibration test frequency and theoretical frequency comparison of the bridge

从表6可知，主桥成桥阶段实测自振频率比理论计算值大，说明成桥阶段结构纵桥向、横桥向、竖向刚度良好。

图7 成桥阶段各测点加速度频谱ig.7 The bridge acceleration spectrum of eachmeasuring point

3 酉水大桥斜交高墩大跨度连续箱梁桥颤振研究

超过一定的风速时，桥梁结构吸收的能力将大于阻尼消耗的能量，该风速成为临界风速Vcr，由于空气动力产生弯曲和扭转的耦合振动，振幅将无限增加至桥梁破坏［6］。对于颤振自激型发散振动，应该使其临界风速提高到高于桥梁在设计使用期内桥位处可能出现的最大风速［7］。

3.1 颤振检验风速

酉水大桥地处V型河谷地带，桥面距离地面的高度为87.16 m，根据《公路桥梁抗风设计规范》［8］，吉首地区100 a重现期的10 min平均年最大风速为24.2 m/s，故得到酉水大桥主梁100 a重现期的设计风速为:

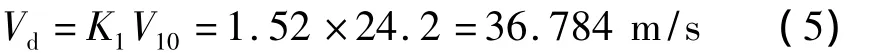
考虑施工阶段设计风速的重现期为10 a，则施工阶段的设计风速为:

颤振检验风速为:

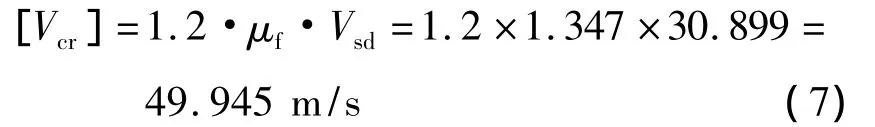
3.2 桥梁结构颤振临界分析

根据《公路桥梁抗风设计规范》可知，对于主跨跨径小于300 m的桥梁，如果其主梁断面的宽高比B/H＜4，则其颤振临界风速的计算公式为:

或者

式中:B为主梁断面宽;H为主梁断面高度;ft为桥梁结构扭转频率。

颤振临界风速取以上两式计算结果的较小者。

当桥面较宽，扭转基频较高，大跨度桥梁的抗风稳定性就越好;反之，当桥面较窄，扭转基频较低，大跨度桥梁的抗风稳定性就越差［9－11］。本桥梁结构桥面宽度为12 m不变，因此选择桥梁结构刚度最小，扭转频率最低时作颤振稳定分析。

从上部分桥梁各施工阶段结构动力特性分析可知，桥梁结构在最大悬臂施工阶段结构刚度小，扭转频率最低，在风荷载作用下容易发生颤振。

根据最大悬臂施工阶段结构动力特性分析结果，计算酉水大桥在最大悬臂阶段扭转基频ft= 1.131 Hz，取B=12 m，H=4 m。因此，临界颤振风速为:

式(8)中:Vcr=67.86 m/s

式(9)中:Vcr=54.288 m/s

故取Vcr=54.288 m/s

由以上的计算结果可知，Vcr＞［Vcr］=49.945 m/s，颤振临界风速大于颤振检验风速，因此桥梁结构在自然风速下不会发生颤振失稳现象。

4 结论

(1)桥梁在最高桥墩施工阶段、最大悬臂施工阶段和成桥阶段3个阶段，桥梁动力特性表现为主桥墩纵漂，在最大悬臂施工阶段，悬臂长度大，结构刚度小，桥墩纵漂明显。

(2)桥梁在最高墩施工阶段、最大悬臂阶段和成桥阶段3个阶段，动力特性实测自振频率比理论值大，说明桥梁在纵桥向、横桥向、竖向刚度良好。

(3)桥梁结构在各施工阶段扭转刚度不大，在最大悬臂施工阶段扭转刚度最小，扭转频率最低，为自然风颤振最不利阶段，其颤振临界风速为54.288 m/s，大于颤振检验风速49.945 m/s，桥梁结构颤振稳定。

［1］颜娟，张哲，黄才良.广东金马大桥动力分析［J］.公路交通科技，2003，20(1):71－73.YAN Juan，ZHANG Zhe，HUANG Cailiang.Dynamic analysis for guangdong jinma bridge［J］.Journal of Highway and Transportation Research and Development，2003，20(1):71－73.

［2］杨永贤，王福敏，周筠莉.城市轻轨连续刚构桥动力特性分析［J］.公路交通技术，2007，(2):94－97.YANG Yongxian，WANG Fumin，ZHOU Yunli.Analysis of dynamic behavior of continuous rigid frame bridge for urban light rail［J］.Technology of Highway and Transport，2007，(2):94－97.

［3］丰硕，项贻强，汪劲丰.大跨径连续刚构桥的动力性能及地震响应分析［J］.中南公路工程，2002，30(4):77－81.FENG Shuo，XIANG Yiqiang，WANG Jinfeng.Analysis on dynamic characteristics and seismic responses for long－span continuous rigid－framed bridges［J］.Central South Highway Engineering，2002，30(4):77－81.

［4］翟建平.肇庆西江特大桥动力特性分析［J］.铁道科学与工程学报，2011，8(3):13－17.ZHAIJianping.Analysis on the dynamic properties of zhaoqing xijiang bridge［J］.Journal of Railway Science and Engineering，2011，8(3):13－17.

［5］王解军，王明明，梁锦锋.变刚度预应力简支梁桥固有振动分析［J］.中南公路工程，2005，30(3):62－64.WANG Jiejun，WANGMingming，LIANG Jinfeng.Natural vibration analysis for a simply supported girder bridge with varying rigidity and prestressing force［J］.Central South Highway Engineering，2005，30(3):62－64.

［6］张迪.龙华特大桥最大悬臂状态抗风分析［D］.哈尔滨:东北林业大学，2007.ZHAGN Di.Analysis of wind resistant of longhua bridge in the longest cantilever state［D］.Harbin:Dongbei Forestry University，2007.

［7］孙娜.桥梁抗风控制及设计探讨［J］.交通标准化，2013 (8):142－144.SUN Na.Control and design of bridge wind－resistant［J］.Communications Standardization，2013(8):142－144.

［8］JTG/TD63－01－200，公路桥梁抗风设计规范［M］.JTG/TD63－01－2004，Design specification for highway bridges［M］.

［9］李国豪.桥梁结构稳定与振动［M］.北京:中国铁道出版社，1992.LI Guohao.Stability and vibration of bridge structure［M］.Beijing:China Railway Press，1992.

［10］张金武，李龙安.公路桥梁抗风设防标准的初探［J］.桥梁建设，2002(3):29－32.ZHANG Jinwu，LI Longan.Discussion and study about anti－wind design criteria for highway bridges［J］.Bridge Construction，2002(3):29－32.

［11］王爱勤，李龙安.公路大跨度桥梁抗风性能评价方法［J］.长安大学学报，2006，26(5):58－62.WANG Aiqin，LI Longan.Evaluation method of windresistance capability of large－span bridge on highway［J］.Journal of Chang＇an University，2006，26(5):58－62.