索夹对自锚悬索桥成桥状态影响分析
孙永明,张连振,李忠龙(哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨150090)
索夹对自锚悬索桥成桥状态影响分析
孙永明,张连振,李忠龙
(哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨150090)
基于有限单元法(FEMC)比较分析了索夹对自锚悬索桥成桥状态的影响.索夹能够提高中跨主缆的成桥线形,在维持索长不变的情况下,各吊杆的成桥索力会有所增大,若使各吊杆均达到设计成桥索力值,则需增大各吊杆的无应力长度值.基于计入索夹影响的FEMC模型分别讨论了索夹长度、截面面积和惯性矩等参数对结构成桥状态的影响,并且建立了根据索夹长度比和面积比计算得到的主缆中跨跨中控制点成桥高程提升量和吊杆索力平均增量值的简化计算公式.经工程实例验证,提出的索夹模型计算结果与结构实际变形接近.
桥梁工程;自锚式悬索桥;索夹;成桥状态
目前,已有关于建立自锚悬索桥整体有限元模型的理论和方法,尤其在分析吊杆成桥索力、主缆成桥线形及在计算吊杆和主缆的无应力长度等结构参数时,均是对吊杆和主缆的连接方式进行了简化处理,直接将主缆和吊杆在其两者中心线交点处相连,而不考虑索夹的影响[1-5].
如图1所示,实际工程中的吊杆和主缆是通过索夹相连.吊杆的集中拉力在经过索夹耳板传递后,变为作用在整个索夹长度范围内的分散力.拧紧后的索夹具备一定的刚度,且由于主缆共同变形受力,使得主缆在索夹紧箍范围内的局部刚度得到了加强.这些导致吊杆和主缆直接在其两者中心线交点处相连的简化分析模型的计算值偏离实际结构的真实变形值.目前,已有的关于索夹的文献[6-7]大多是对索夹自身强度和抗滑性能的研究,而对索夹调整吊杆与主缆的传力方式,增强主缆局部刚度,进而影响主缆结构状态的研究文献甚少.鉴于此,本文展开了关于索夹对自锚悬索桥成桥状态影响的深入研究.

图1 通过索夹连接的主缆和吊杆Fig.1 Main-cable and boom connected by cable clamp
1 结构参数和索夹模型
如图2所示,吉林市雾凇自锚悬索桥采用预应力钢筋混凝土主梁,其跨径布置为35m+68m+150m+68m+35m=356m;该桥为钢筋混凝土门字形主塔,桥面以上建筑高度为31m;2根主缆分布在主梁两侧,每根主缆均由37根索股组成,每根索股由127根φ5.1mm高强钢丝组成,其在成桥状态下的矢跨比为1/5;主索鞍半径为3.5m;全桥共49对吊杆,吊杆在梁上的间距为5m.
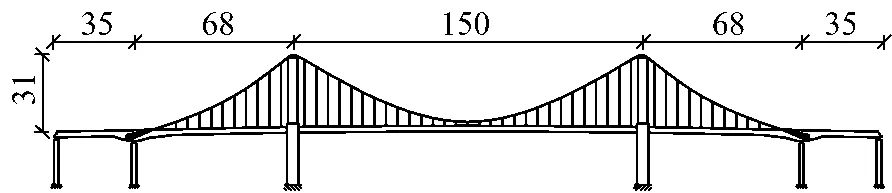
图2 五跨自锚悬索桥立面图(单位:m)Fig.2 Five-span self-anchored suspension bridge(unit:m)
基于悬索桥分析程序PNAS[8]建立雾凇大桥平面有限元模型FEMR和FEMC.常规模型FEMR不考虑索夹的影响,其吊杆和主缆直接在两者中心线交点处相连;而细化分析模型FEMC则考虑索夹的影响,采用独立的234模型对索夹进行模拟.
如图3所示,采用2个梁单元模拟索夹主体,考虑索夹的抗弯刚度和抗拉刚度;采用3个杆单元模拟耳板,将吊杆的集中拉力分散到整个索夹上.其中,4号节点表示吊杆上端销轴中心,2号节点表示主缆与吊杆中心线交点,而1号和3号节点分别为索夹上下口与主缆中心线交点.索夹4号节点直接与吊杆相连,索夹1~3号节点均与主缆采取主从约束的方式相连,主缆为主,索夹为从.

图3 索夹有限元模型Fig.3 Finite element model of cable clamp
2 索夹对成桥状态影响分析
2.1 考虑索夹影响的成桥状态计算
已知主缆设计成桥线形C(D)C和吊杆设计成桥索力F(D)C.首先,基于FEMR模型对结构进行反复正装分析[9],获得主缆无应力长度S(R)0和吊杆无应力长度L(R)0.然后,将S(R)0和L(R)0代入FEMC模型内,分析主缆和吊杆在索夹影响下的成桥线形C(C)C和成桥索力F(C)C.
在具有相同结构参数S(R)0和L(R)0的条件情况下,基于模型FEMR获得的主缆成桥线形和吊杆成桥索力均能够达到设计成桥值,即C(R)C=C(D)C和.但是,基于模型FEMC获得的主缆成桥线形和吊杆成桥索力均会偏离设计成桥值,即和.如表1所示,计入索夹影响的主缆中跨跨中控制点成桥高程值C(C)C比设计成桥值C(D)C高48mm.如图4所示,计入索夹影响的各吊杆成桥索力值F(C)C均大于设计成桥索力值F(D)C==2 100kN,位于主塔两侧的长吊杆索力偏差可达168kN.
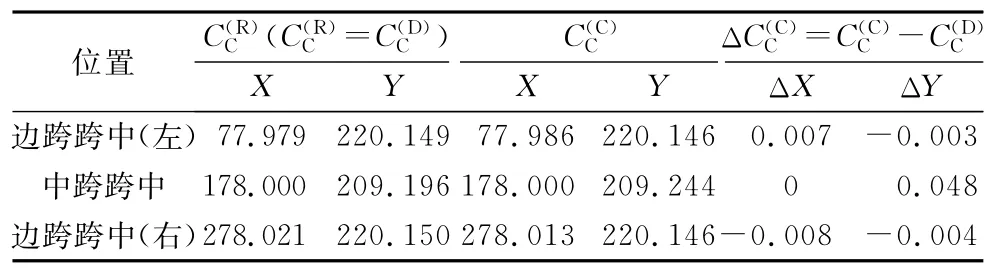
表1 索夹对主缆成桥线形影响Tab.1 Impact of cable clamp on the completed shape of __main cable
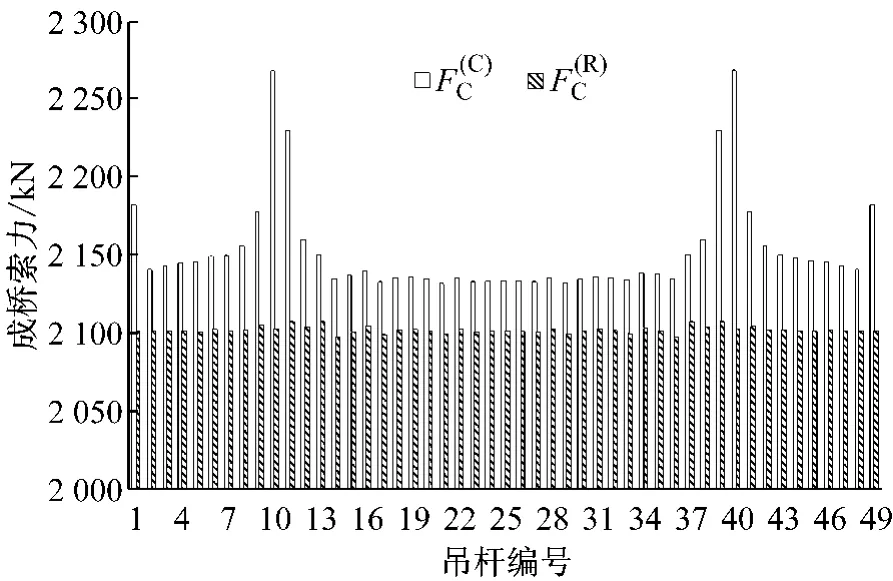
图4 考虑索夹影响的各吊杆成桥索力值Fig.4 Completed force of boom considering the effect of cable clamp
继续在模型FEMC中分析.将各吊杆索力F(C)C调整为设计成桥索力F(D)C,获得各吊杆在索夹影响下的无应力长度值L(C)0,分析索夹对吊杆无应力长度的影响,ΔL(C)0=L(C)0-L(R)0.如图5所示,计入索夹影响的各吊杆无应力长度值L(C)0均大于未考虑索夹影响的无应力长度值L(R)0,其位于中跨跨中的短吊杆无应力长度偏差可达41mm.

图5 索夹对吊杆无应力长度影响Fig.5 Impact of cable clamp on the unstressed length of booms
上述分析结果表明,索夹能够对自锚悬索桥的成桥状态构成影响,其影响量在实际工程中不容忽视,建议在自锚悬索桥分析模型中,尤其在计算吊杆和主缆的无应力长度时,应考虑索夹的影响.
2.2 索夹参数影响分析
基于细化分析模型FEMC分析索夹各参数对主缆成桥线形和吊杆成桥索力的影响,以主缆中跨跨中控制点成桥高程值的差值=,来表征索夹对主缆成桥线形的影响.以各吊杆成桥索力值F(C)C,i与F(D)C,i的差值平均值,来表征索夹对吊杆成桥索力的影响.
索夹主要包括3个计算参数:抗拉面积AC、抗弯惯性矩IC和水平投影长度DC.设吊杆标准间距DB,主缆半径RS,计算面积AS=πR2S,计算惯性矩IS=πR4S/4,则索夹的抗拉面积比KA=AC/AS、索夹的抗弯惯性矩比KI=IC/IS和索夹的长度比KD=DC/DB.
如图6所示,在面积比KA=0和惯性矩比KI=0的情况下,主缆成桥线形C(C)C会随着索夹长度DC的增加而有所提升,中跨跨中控制点成桥高程的提升量.吊杆成桥索力F(C)C会随着索夹长度DC的增加而有所增大,各吊杆索力增量的平均值≈130 K.索夹长度影响的实质是将本来集
D中作用在销轴中心点处的吊杆拉力,分散作用在整个具有索夹紧箍区域的主缆上,其效果类似于简支梁在跨中承受竖向集中力和具有相同重力的竖向均布荷载,而后者产生的挠度较小.所以说,索夹越长,吊杆拉力分散范围越大,主缆成桥线形和吊杆成桥索力所受到的影响就越显著.

图6 索夹长度比对主缆线形和吊杆索力的影响Fig.6 Impact of cable-clamp length ratio on main-cable shape and boom force

图7 索夹面积比对主缆线形和吊杆索力的影响Fig.7 Impact of cross-section area ratio of cable clamp on main-cable shape and boom force
如图7所示,在惯性矩比KI=0和长度比KD=0.2的情况下,主缆成桥线形C(C)C会随着索夹抗拉面积AC的增加而有所提升,中跨跨中控制点成桥高程的提升量ΔC(C)C,m≈60 KA;吊杆成桥索力F(C)C会随着索夹抗拉面积AC的增加而增大,各吊杆索力增量的平均值≈40 KA.索夹抗拉面积影响的实质是增大了具有索夹紧箍区域的主缆抗拉面积,进而改变了主缆成桥线形和吊杆成桥索力.但是,索夹紧箍主缆所产生的摩擦力主要是保证两者不会在吊杆力的作用下发生相对滑动,并不是确保两者在主缆拉伸的情况下仍能保持同步变形,所以在实际工程中,索夹的抗拉面积并不能全部计入主缆的有效抗拉面积.
如图8所示,在面积比KA=0和长度比KD=0.2的情况下,索夹抗弯惯性矩对主缆的成桥线形C(C)C和吊杆的成桥索力F(C)C均影响甚微.但是,由于吊杆拉力最终作用在主缆上的长度范围和分散力大小均受到索夹抗弯惯性矩的影响,所以从分散吊杆集中力的角度分析,索夹抗弯惯性矩对结构成桥状态起着不可忽视的影响.

图8 索夹惯性矩比对主缆线形和吊杆索力的影响Fig.8 Impact of cross-section moment ratio of inertia of cable clamp on main-cable shape and boom force
3 工程实例分析
3.1 计算参数和实测数据
吉林市雾凇大桥的桥跨布置和各结构参数如前文所述,全桥共49对索夹,分为5种型号(SJ1~SJ5),每种型号索夹具有相同的抗拉面积AC=1 211 cm2和抗弯惯性矩IC=438 594cm4,以及不同的水平投影长度DC=68~156cm,各种索夹的具体水平投影长度和布置情况如表2所示.

表2 索夹水平投影长度和布置情况Tab.2 Horizontal projected length and arrangement of cable clamps
根据实测的主缆空缆线形C(M)0和成桥线形(见表3),以及各吊杆在成桥状态下的锚杯外露量和频率值(见表4)[10-11],进而获得各吊杆无应力长度值L(M)0和索力值F(M)C.

表3 实测的主缆空缆线形Tab.3 Measured unloaded shape of main cable m

表4 实测的各吊杆无应力长度值和索力值Tab.4_Measured unstressed lengths and pullingforces of booms

表5 主缆成桥线形汇总Tab.5 Summary of main-cable shape on the completed stage of bridge m
3.2 吉林市雾凇大桥成桥状态分析
将各索夹的实际参数值、主缆的实测空缆线形值C(M)0和吊杆的实测成桥无应力长度值L(M)0代入模型FEMR和FEMC内,分别计算结构在成桥状态的主缆线形值C(R)C和C(C)C、吊杆索力值F(R)C和F(C)C,并将其与主缆的实测成桥线形C(M)C和吊杆的实测成桥索力F(M)C进行比较,计算线形偏差ΔC(R)C=计算索力偏差
如表5所示,基于模型FEMR和FEMC获得的主缆边跨成桥线形基本一致,且均与实测值比较接近.但不考虑索夹影响的主缆中跨跨中控制点成桥高程值与实测高程值相差较大,其计算值比实测值低0.077m.计入索夹影响后的主缆中跨跨中控制点成桥高程值与实测值吻合较好,其计算值只比实测值高0.014m.

表5 主缆成桥线形汇总Tab.5 Summary of main-cable shape on the completed stage of bridge m
如图9所示,基于模型FEMC获得的未考虑索夹影响的吊杆成桥索力值F(R)C总体上小于实测成桥索力值F(M)C,最大索力偏差ΔF(M)C,max=-200kN;而基于模型FEMC获得的计入索夹影响的吊杆成桥索力F(C)C总体上更接近于吊杆实测成桥索力值F(M)C,其最大索力偏差ΔF(C)C,max=-105kN.
工程实例分析结果表明,索夹能够使主缆中跨成桥线形提高0.077m,各吊杆最大成桥索力偏差为-200kN,该偏差值已超出工程容许范围,应予以调整;而基于模型FEMC获得的主缆成桥线形和吊杆成桥索力计算值均与实测数据吻合得较好,说明本文提出的索夹模型合理,模拟方法正确,能够准确、有效地反映索夹对结构的影响.
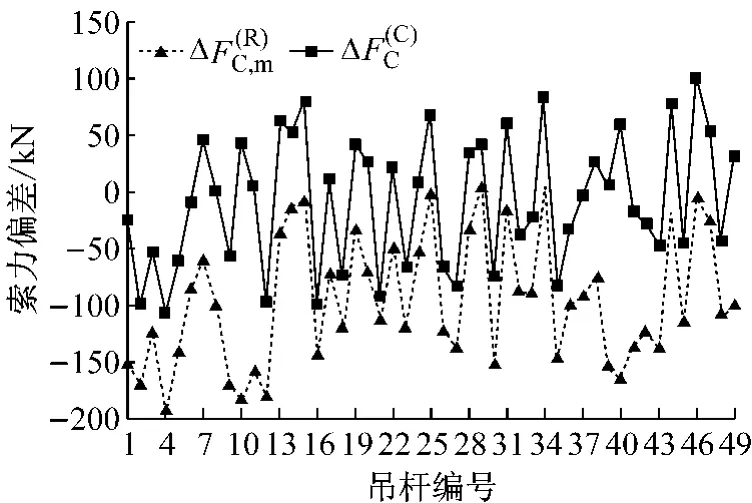
图9 计算索力与实测索力偏差图Fig.9 Deviation of boom force between calculated and measured values
4 结论
(1)索夹能够对自锚悬索桥的成桥状态造成影响,使主缆的成桥线形有所提升.若维持各吊杆无应力长度不变,则吊杆的成桥索力普遍增大.若使各吊杆索力达到成桥索力值,则需加大各吊杆的无应力长度值.
(2)主缆成桥线形和吊杆成桥索力主要受索夹的抗拉面积和水平投影长度影响,受索夹抗弯刚度的直接影响甚微;主缆中跨跨中控制点成桥高程提升量≈60 KA+60 KD,各吊杆成桥索力平均增量≈40 KA+130 KD.
(3)经工程实例验证,本文所提出的索夹模型合理,模拟方法正确,能够正确、有效地反映索夹对结构的影响,其计算结果与结构的实际变形值更为接近.
在进行自锚式悬索桥设计过程中,尤其在进行主缆和吊杆无应力长度计算时,应考虑索夹的影响.同时应注意索夹的抗拉面积并不能全部计入主缆的有效抗拉面积,在具体分析时应予以折减.
[1]孙永明,张连振,李忠龙.自锚式悬索桥主缆状态影响参数分析[J].计算力学学报,2014,31(6):742.SUN Yongming,ZHANG Lianzhen,LI Zhonglong.Analysis of the parameters infulencing the main-cable state of self-anchored suspension bridge[J].Chinese Journal of Computational Mechanics,2014,31(6):742.
[2]孙永明,张连振,李忠龙.自锚式悬索桥吊杆目标索力影响参数分析[J].桥梁建设,2015,45(4):69.SUN Yongming,ZHANG Lianzhen,LI Zhonglong.Affectingfactor study on boom’s target force of self-anchored suspension bridge[J].Bridge Construction,2015,45(4):69.
[3]沈锐利.悬索桥主缆系统设计及架设算法研究[J].土木工程学报,1996,29(2):3.SHEN Ruili.Calculation methods for design and erection of cable curve of suspension bridge[J].China Civil Engineering Journal,1996,29(2):3.
[4]陈常松,陈政清,颜东煌.悬索桥主桥初始线形的悬链线方程精细迭代分析法[J].工程力学,2006,23(8):62.
CHEN Changsong,CHEN Zhengqing,YAN Donghuang.Accurate interation method to calculate the initial states of main cables of suspension bridges[J].Engineering Mechanics,2006,23(8):62.
[5]程斌,孙海涛,肖汝诚.自锚式悬索桥的主缆线形计算与误差分析[J].华南理工大学学报:自然科学版,2008,36(6):17.CHENG Bin,SUN Haitao,XIAO Rucheng.Configuration calculation and deviation analysis on main cable of self-anchored suspension bridge[J].Journal of South China University of Technology:Natural Science Edition,2008,36(6):17.
[6]黄海云,张俊平,刘爱荣,等.空间索面自锚式悬索桥主缆横向位移及索夹横向偏转角的试验研究[J].公路工程,2009,34(2):41.HUANG Haiyun,ZHANG Junping,LIU Airong,et al.Testing study on lateral displacement of main cable and lateral deflection angle of cable clamp in the self-anchored suspension bridge with spatial cable system[J].Highway Engineering,2009,34(2):41.
[7]黎志忠,蒋劲松.悬索桥上、下对合型索夹结构分析研究[J].桥梁建设,2013,43(3):60.LI Zhizhong,JIANG Jinsong.Analysis and study of cable band structure of upper and lower halves type for suspension bridge[J].Bridge Construction,2009,43(3):60.
[8]孙永明.基于组合单元的混凝土斜拉桥施工过程分析与控制方法研究[D].哈尔滨:哈尔滨工业大学,2009.SUN Yongming.Construction process analysis and construction control techniques research of concrete cable-stayed bridge based on composite element[D].Harbin:Harbin Institute of Technology,2009.
[9]刘厚军,刘钊.自锚式悬索桥吊索张力及主缆线形的设计研究[J].土木工程学报,2008,41(3):79.LIU Houjun,LIU Zhao.Design of hanger tension and cable configuration for self-anchored suspension bridges[J].China Civil Engineering Journal,2008,41(3):79.
[10]孙永明,孙航,任远.频率法计算匀质竖直拉索索力的实用公式[J].工程力学,2013,30(4):211.SUN Yongming,SUN Hang,REN Yuan.Practical formulas to calculate tensions of vertical cable with uniform properties by frequency method[J].Engineering Mechanics,2013,30(4):211.
[11]孙永明,李惠.端部性质对频率法测量竖直拉索索力影响分析[J].工程力学,2013,30(8):10.SUN Yongming,LI Hui.Effect of extreme properties of vertical cable on the cable force measurement by frequenciesbased method[J].Engineering Mechanics,2013,30(8):10.
Impact Analysis of Cable Clamp on Completed State of Self-anchored Suspension Bridge
SUN Yongming,ZHANG Lianzhen,LI Zhonglong
(School of Transportation Science and Engineering,Harbin Institute of Technology,Harbin 150090,China)
The impacts of cable clamps on the completed state of a self-anchored suspension bridge were analyzed based on the finite element method(FEMC).The cable clamp could raise the shape of main cable in a middle span.If the unstressed length of each boom was kept unchanged,the pulling force of each boom would increase.In the same way,if each boom was made to reach the designed force on the completed stage of a bridge,the unstressed length of each boom should be increased.Based on FEMC,the impacts of parameters,e.g.length,cross-sectional area and moment of inertia on the completed state of a bridge,were studied respectively.Furthermore,the simplified formulas were established,which could calculate the elevation increment of mid-position of main cable in the middle span and the average increment of each boom force by the length ratio and area ratio of cable clamp.It is verified that results from FEMCare in good agreement with the measured data.
bridge engineering;self-anchored suspension bridge;cable clamp;completed state of a bridge
U448.25;U443.38
A
0253-374X(2016)01-0024-05
10.11908/j.issn.0253-374x.2016.01.004
2015-01-04
国家自然科学基金(51308156);中国博士后科学基金(2012M510969);中央高校基本科研业务费专项资金(HIT.NSRIF.2014077)
孙永明(1981—),男,工学博士,主要研究方向为混凝土结构安全评定、结构有限元分析原理和桥梁施工控制理论.E-mail:sunym@hit.edu.com

