基于末端杆件姿态约束的串联机器臂避碰策略
王恒升,黄平伦,彭天博(1.中南大学高性能复杂制造国家重点实验室,湖南长沙410083;.中南大学机电工程学院,湖南长沙410083)
基于末端杆件姿态约束的串联机器臂避碰策略
王恒升1,2,黄平伦2,彭天博2
(1.中南大学高性能复杂制造国家重点实验室,湖南长沙410083;2.中南大学机电工程学院,湖南长沙410083)
根据双臂凿岩台车上六自由度串联机械臂的工作特点,为减小机械臂运动干涉的可能性,提出了该机械臂在运动过程中保持末端杆件垂直于工作断面的姿态约束条件,并给出实现这一约束条件的运动学方法和空间杆件发生干涉的判断式.针对某隧道断面64个炮孔设计,对机械臂运动进行了仿真,结果表明文中所提方法具有良好的避碰效果.
六自由度串联机械臂;避碰;运动干涉;姿态约束
机器人运动干涉(避碰)问题的解决往往与路径规划联系在一起.过去几十年来,这一问题的研究范围包括移动机器人路径规划、多机器人路径规划、串联(并联)机械臂的路径规划等[1-2].针对机器臂来说,路径规划的任务就是要在机械臂起点位姿和终点位姿之间寻找一条路径,沿着这条路径驱动关节变量向目标位姿运动的过程中,机械臂的各个杆件不会发生任何形式的碰撞(或称运动干涉),包括一个机械臂的各杆件之间、几个机械臂的杆件之间、机械臂与环境及障碍物之间.
路径规划及避障的研究大致可分为2类方法:
一类是基于规划的方法(或离线方法),一般是对机械臂的工作空间进行离线规划,搜索出一条最优路径.20世纪70年代,文献[3-4]做了开创性的工作.文献[4]提出的C-空间法对路径规划的研究起了非常深远的影响,很多研究工作都是基于C-空间提出的.实际算法在应用时需要对这一位姿空间进行离散化,如将上述平面分割成许多小方格(称为网格),自由区域用0表示,有干涉区域用1表示.典型的基于离散化位姿空间的最短路径搜索方法有Dijkstra算法和A*算法.八叉树、Voronoi图、概率地图等提供了不同的表示位姿空间的方法[2-5].位姿空间法的明显不足是,随着机械臂自由度数目的增加,位姿空间会向高维发展,所需要的存贮空间、计算搜索时间和计算复杂度会迅速增加,无法实际应用.很多研究工作就是想办法使位姿空间适合于多自由度机械臂的应用.
另一类方法是基于控制提出的,试图通过实时控制来实现避障及搜索最优路径.典型的方法有人工势函数法[6]和反射控制法[7].人工势函数法建立一个势场,该场吸引机械臂向其目标位姿移动而同时排斥其远离障碍物,通过搜索势函数的梯度方向来寻找最优路径.反射控制法涉及到快速评估机械臂的运动干涉情况,如有碰撞的可能,就采取措施避开障碍物.反射控制法常常通过安装传感器实现快速准确判断障碍物的方位.与基于规划的方法相比,基于控制的方法属于在线的局部寻优法,容易陷入局部最优而无法到达目标位姿.为了跳出局部最优,基于控制的方法往往需要在控制结构中引入全局路径规划,非常消耗计算资源.
值得一提的是,近来年,碰撞干涉检测问题在计算机图形的应用方面,如动画、三维可视化几何处理、计算机游戏等,取得不少的研究成果[8-10].
本文针对一种六自由度机械臂,提出以末端执行器的姿态为约束,不需要建立C-空间.在机械臂的运动过程中,只要保持末端执行器姿态固定,就可以大大减小机械臂运动干涉的可能性,同时大大减小实时控制器在避碰方面的计算压力.再辅之以障碍检测传感器,可以很好地防止机械臂的运动干涉.
这一思路受到冗余机械臂自运动的启发[11-15].对于冗余机械臂,相应于末端执行器的某目标位姿,关节变量有多种(甚至于无穷多种)配置.这个特点使冗余机械臂为达到末端执行器的某种工作位姿,可以克服关节的限制、奇异位形或改善动力学性能,也可以绕过障碍物,同时还可以用于末端执行器需要锁定在某确定位姿而调整关节以实现避障、多机械臂协作及某特定作业(如医疗外科、拧开瓶盖等)的情况.
六自由度机械臂在关节配置的灵活性上不如冗余机械臂,无法实现末端执行器位姿固定调整驱动关节位置,但可以放松自运动中对末端执行器位姿固定的这一约束,仅保持末端执行器姿态不变或者姿态的某些参数不变.针对凿岩机械臂的工作特点,本文提出末端执行器的姿态保持垂直工作面的避障运动约束条件.
1 末端杆件姿态确定
研究对象为双臂凿岩台车上的六自由度机器臂.凿岩台车的末端执行器是液压凿岩钻机,安装在图1所示的滑架上.滑架上装有3m多长的钻钎,工作时要求在岩石断面上打出一定深度的炮孔.机械臂的作用就是根据爆破工艺的设计要求,将滑架以某姿态移动到断面的指定位置.对于4.8m宽的煤矿运煤通道,通道断面的一次爆破成形需要60~80个炮孔,2个机械臂同时工作.机械臂的运动干涉可能发生在机械臂杆件之间,也可能发生在2个机械臂之间,还有可能发生在机械臂与隧道壁之间.由于该机械臂的质量和尺寸较大,发生碰撞后引起的破坏性很大.目前国内使用的液压凿岩台车大多是手动操作,避碰是由操作人员手动掌握的.将自动控制技术与机器人技术应用于凿岩台车,实现某种程度的自动化作业,可以大大减少操作人员的劳动强度.
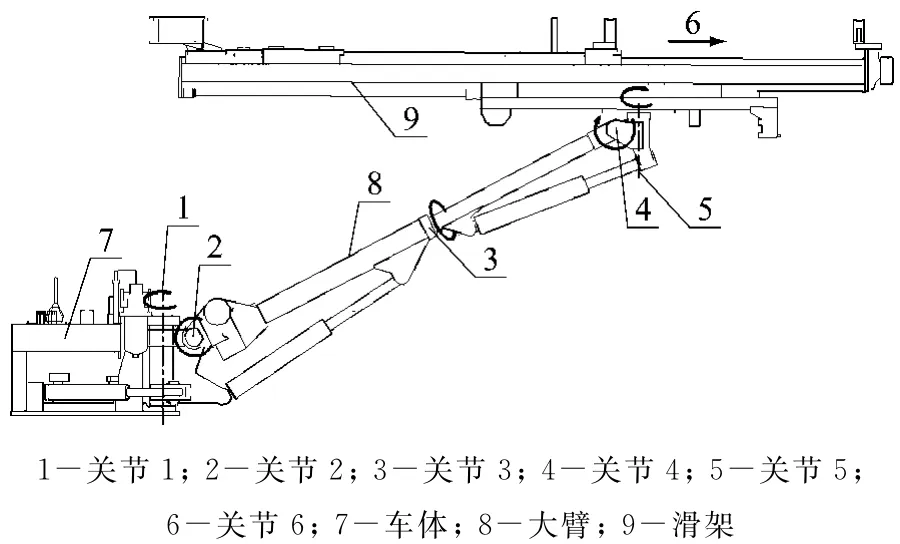
图1 机械臂外形Fig.1 Outline of the manipulator
凿岩台车机械臂外形如图1所示,机械臂机构简图如图2所示.图2表达出了固结于每个关节的坐标系设置.机械臂共有6个关节,前5个关节为转动关节,最后1个是移动关节.本文提出机械臂运动过程中保持末端杆件(即滑架)的姿态垂直于工作断面的方法,主要基于以下原因:
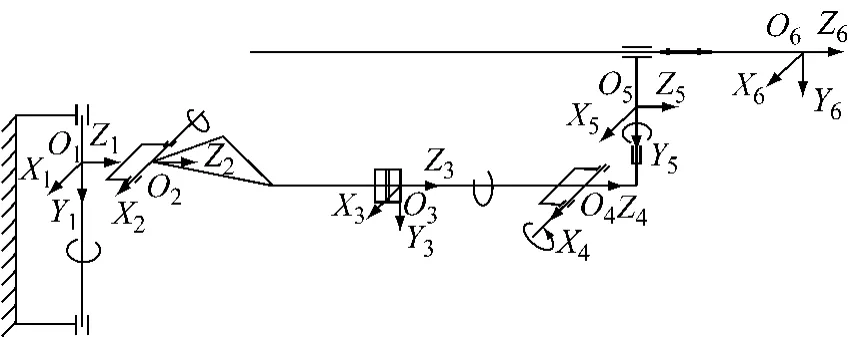
图2 机械臂机构简图Fig.2 Mechanism of the manipulator
(1)根据爆破工艺,炮孔的姿态设计要求打孔时滑架的姿态基本接近于与断面相垂直,只有掏槽孔和外沿孔有一定的偏角要求,但偏转的角度不大,一般在30°以内.因此,滑架在运动过程中保持与断面垂直,在接近目标点时再调整最终姿态不会造成机械臂运动的不平稳.
(2)机械臂运动过程中末端杆件保持与断面垂直,可以减小机械臂的空间活动范围与空间占用.图3b和3c分别为滑架垂直断面和不垂直断面时机械臂在断面上的投影示意图,很明显滑架垂直断面时机械臂与隧道壁以及2个机械臂之间碰撞的可能性大为减小.
(3)滑架与断面垂直,可以有效减少单个机械臂自身干涉的可能性,如图4所示.图4 机器臂两杆件间的自干涉
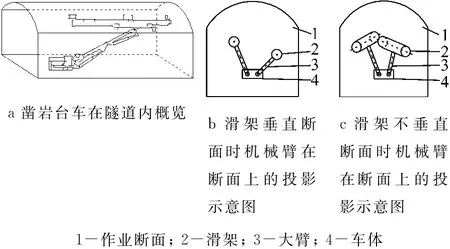
图3 凿岩台车在隧道内示意图Fig.3 Sketch of tunnelling rig in workplace
Fig.4 Self-interference of the manipulator between two links
2 滑架保持垂直于工作断面的实现
用四元数法[16-20]建立Oi-XiYiZi(i=1~6)坐标系,如图2所示.这里的杆件坐标系全部采用同一姿态,可以更直观地理解关节的运动.
5个转动关节轴在相应关节坐标系中的矢量表达分别为e2、e1、e3、e1、e2,其中e1、e2、e3分别表示相应坐标系X、Y、Z轴方向的单位矢量.旋转变量为θ1、θ2、θ3、θ4、θ5.在机械臂运动学逆解完成以后,各个炮孔所对应的关节变量值均已确定.接下来的任务是确定角度θ4、θ5,使机械臂从一个孔到另一个孔的运动过程中始终保持滑架与断面垂直,也即在实际控制中根据关节角度传感器测量得到θ1、θ2、θ3的值,然后确定θ4、θ5的跟随值,其约束条件就是保证滑架垂直于工作断面.当机械臂θ1、θ2、θ3接近目标
从机械臂的运动学特性可知(见图1和2),末端执行器目标位置的驱动主要由关节1和2来实现,关节3~5主要用于调节末端执行器的姿态,其中关节3的作用是在打周边孔时防止机械臂上附带的油路管道对钻臂运动产生影响.在运动中为实现滑架姿态始终垂直工作断面,需要按关节1~3的角度调整关节4和5的角度,下文详细推导这一约束关系.位姿时,再调整θ4、θ5,达到目标位姿.
在下面的推导中用到的几个标志矢量所对应的四元数定义为:①工作断面法向量的四元数,N=(0,e3)=(0,0,0,1);②关节4的虚拟法向量四元数,N4=(0,e2)=(0,0,1,0);③关节5的虚拟法向量四元数,N5=(0,e1)=(0,1,0,0).关节1~5的旋转运动用四元数可以分别表示为
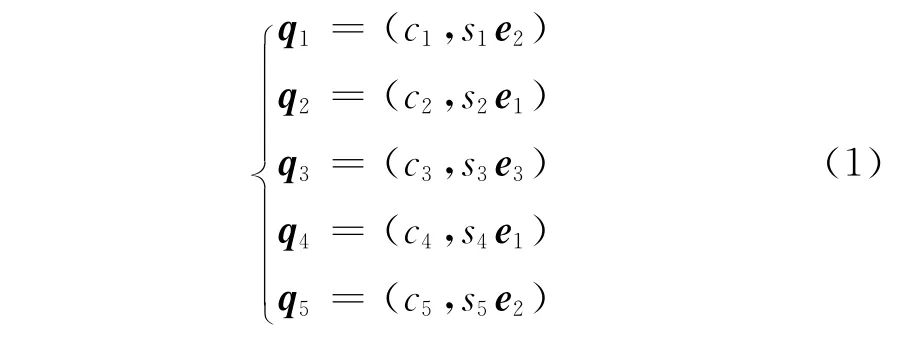
式中:ci表示cos(θi/2),si表示sin(θi/2),i=1~5.
由于仅涉及到杆件的姿态,未涉及位置量,所以推导过程只运用坐标的旋转变换.
关节1~3的连续旋转变换的四元数运算为

其结果Q3亦为单位四元数,并记为

其中a、b、f、r为实数,而且满足关系
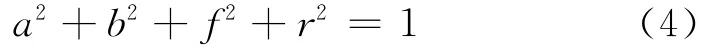
加入关节4的旋转变换为
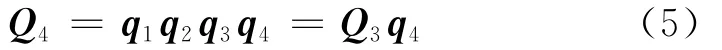
将式(1)和(3)代入式(5),有
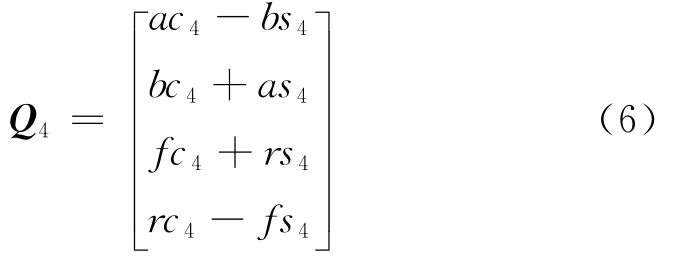
若要机械臂在运动过程中保持滑架姿态垂直于工作断面,则关节4的虚拟法向量与断面法向量必须正交.利用四元数法,关节4的虚拟法向量(四元数)N4经过前面4个关节的旋转变换后得到的四元数为Q4N4Q-14,该四元数是一个纯矢量,应与断面法向量相垂直.按照此约束条件,可以得到
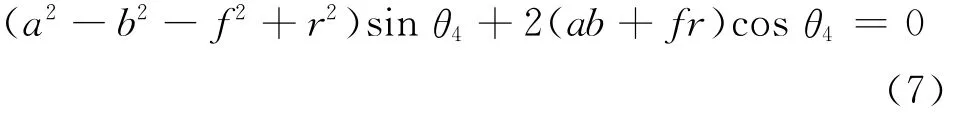
记
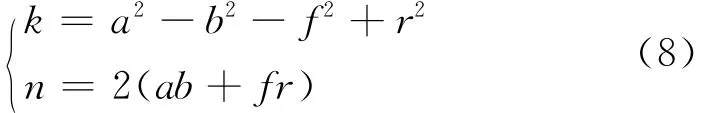
式(7)可简化为
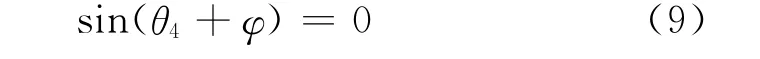
根据几何意义,可以得到

其中,
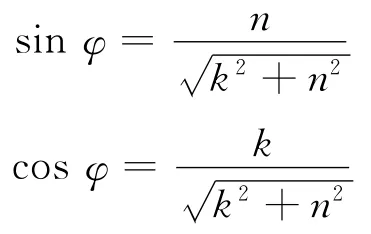
下面说明θ5的求解.经过前面4个关节的旋转后,为保持滑架垂直断面,关节5的虚拟法向量N5与断面法向量之间应该成直角,如果不是直角可通过关节5调成直角,这就是关节5需要调整的角度.
设关节5的虚拟法向量(四元数)N5经过前面4个关节旋转后变换为N′5,根据四元数运算法则,有


其中Q4由式(5)得到.关节5的调整角度
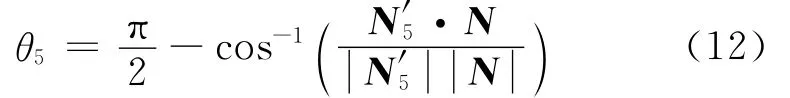
为简化符号表达,式(12)中直接用四元数的符号来表示其对应的矢量运算.式(10)和(12)即为保持滑架垂直所需要的θ4、θ5跟随θ1、θ2、θ3变化的关系式.
3 滑架保持垂直于作业断面方法的仿真证明
按照上述方法,直观上能使机械臂杆件运动所占用的空间小,有利于防止运动干涉.下面定量计算按照这种控制策略运动时机械臂杆件之间的距离,用于检测杆件运动过程中发生干涉的可能性.这里将空间杆件简化为空间线段,如图5中的AB和CD表示2个空间杆件.
3.1 干涉的判断
设2个杆件所在直线分别为L1和L2,2条直线的公垂线为GG′,如图5所示.为便于后文求解G、G′的坐标,这里引入直线的Plücker坐标[19].在某坐标系下,Plücker坐标用2个向量表达1条直线,将直线L表达为形如
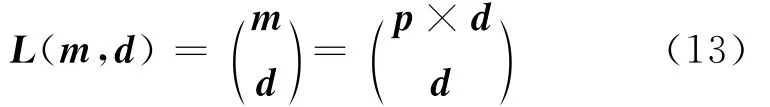
的1个6维向量.其中,d为直线的单位方向向量;m为直线相对于坐标原点的矩(向量),由m=p×d确定,p为坐标原点连接该直线上任意一点构成的向量;d和m正交,即d·m=0.如图5所示,2个杆件AB和CD所在的2条直线L1和L2的Plücker坐标分别为L1(p1×d1,d1)、L2(p2×d2,d2).其中,p1、p2分别为向量,P1和P2为直线L1和L2上的任意点,d1和d2为直线L1和L2的单位方向向量.令g、g′分别表示向量,则公垂线GG′所在直线的Plücker坐标为
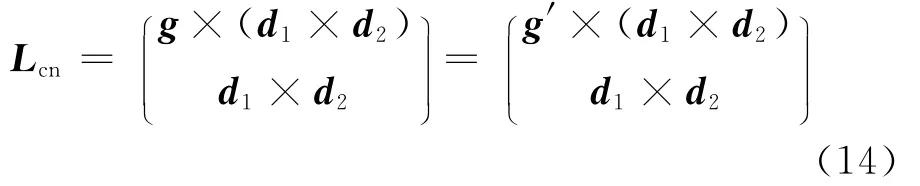
垂足G、G′的坐标计算可参照图5列出的向量运算式得到,如下所示:
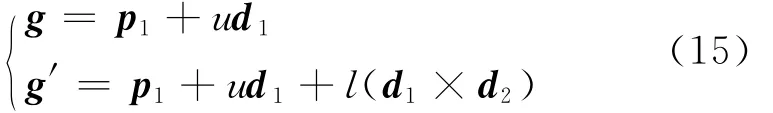
其中的实系数u、l可由式(16)给出的向量约束方程求解,P1和P2为直线L1和L2上的任意点,可分别选已知坐标的A点和C点.由图5的几何关系可以写出式(16),其中h为一实数.
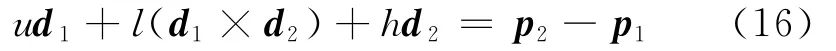
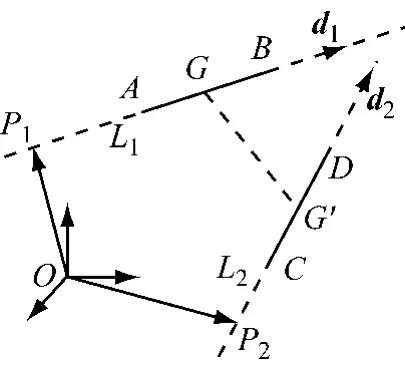
图5 Plücker坐标及空间2条直线的距离Fig.5 Plücker coordinate and the distance between two lines in space
至此,垂足G、G′的坐标可以通过式(15)和(16)轻松求得.接下来讨论3类9种距离.
3.1.1 第1类距离
传统的成本管理过分强调“省”和“节流”,努力追求成本最小化,结果使成本管理仅仅限制在生产领域当中,这种方式把直接材料、直接人工,和制造费用当作减少成本费用的主要技巧,因此成本管理陷入了一个简单的循环,成本的减少并不能够提供最终的决策所需要的有效信息,无法准确的表现出整个经营活动过程,更不能具体的表现出每一个环节的成本信息。反而更多的关注点放在了生产过程中的节省,这样造成了在过程当中核算的比较多,但是前期的预测和准备较少,成本管理效果非常弱。
2个杆件所在直线L1和L2之间公垂线的距离,即图5中公垂线GG′的长度.可分以下2种情况确定公垂线的长度:
(1)垂足G、G′都落在对应线段内部,且d1× d2≠0时,根据公垂线段距离公式计算
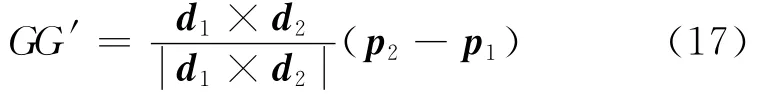
(2)除去(1)的情况,即d1×d2=0时或者至少有1个垂足点没有落在对应线段内部时,式(17)计算出的公垂线长度对判断干涉没有意义,此时取GG′=+∞.线段之间的最短距离可能是以下几种情况之一:线段端点向另一线段的投影垂直距离(本文称为第2类距离),即AA′、BB′、CC′、DD′之一;两线段端点之间的连线距离(本文称为第3类距离),即AC、AD、BC、BD之一.
3.1.2 第2类距离
线段端点向对应线段的投影点在对应线段内,投影垂直距离有AA′、BB′、CC′、DD′4种,其中符号A′表示A点在线段CD上的投影点,其他类推.先分析端点A投影到CD所在直线A′点的距离AA′的计算,如图6所示,按照投影点的位置分为3种情况.判断此3种情况可概括为下面判别式的计算,根据3个端点的坐标可得到
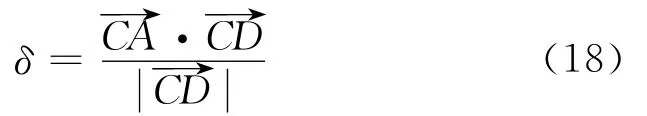
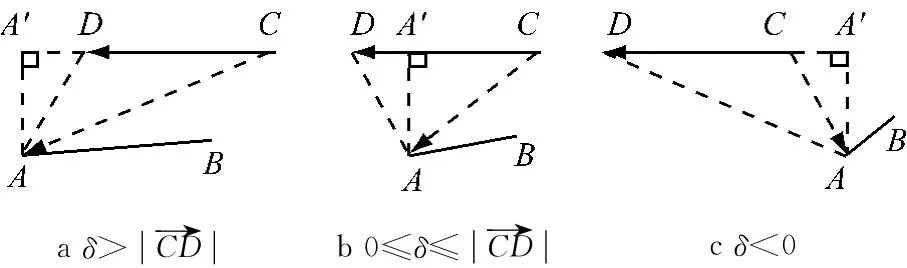
图6 线段端点向另一线段投影情况Fig.6 Cases of projection to another line from one line in space
(3)δ<0,即图6c的情况.
对于第2类距离的(1)、(3)2种情况,A′点不在CD线段内,此时距离AA′对干涉的判断没有影响,此距离可不计算在内,判断时可取AA′=+∞.对于情况(2),A′在线段CD段内,对杆件的干涉判断有影响,距离AA′=
3.1.3 第3类距离
线段端点向另一线段的投影点不在对应线段内时,计算2条线段端点之间的连线距离,即AC、AD、BC、BD4种,根据4个端点的坐标,利用欧拉距离公式可计算出这些距离.
按照以上分析计算出2个杆件的3类9种距离,取其中的最短距离
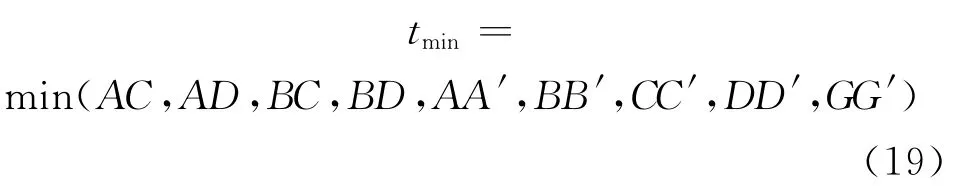
来判断2个杆件的干涉情况.由于tmin是杆件中心轴之间的距离,因此还应该考虑杆件的尺寸.将2个杆件考虑为半径分别为R1、R2的2个圆柱体,判断2个杆件的碰撞干涉可用如下的判断式:
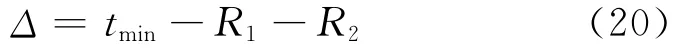
Δ≤0时,两杆件有碰撞干涉发生;Δ>0时,无碰撞发生;Δ值越大,发生碰撞干涉的可能性越小.
3.2 仿真
图7所示为台车应用的某煤矿运煤隧道断面的64个炮孔位置设计,用虚线给出了一种左右臂钻孔的孔序规划.右臂从58号孔开始,沿着虚线指示的路径,最后到63号孔结束;左臂从11号孔开始,到1号孔结束.
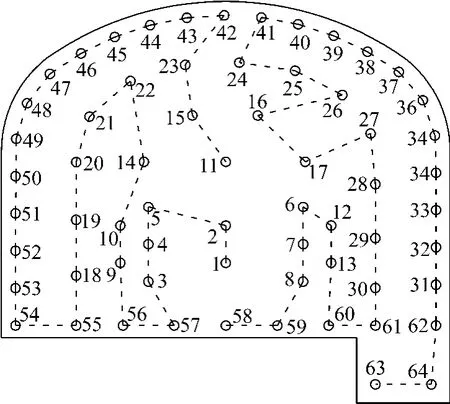
图7 断面炮孔布置及左右臂作业孔序路径图Fig.7 Borehole design pattern on working section and boring sequence paths of right and left manipulators
3.2.1 仿真1:2个孔位之间机械臂的移动仿真本文所讨论的机械臂的末端执行器(凿岩机及钻钎)安装在末端杆件(即滑架)上,工作时,机械臂根据爆破工艺设计的炮孔的位置和方向,将滑架移送到目标位置和姿态.如果在移动过程中没有对末端执行器的姿态进行约束,这4m多长的杆件在空中摆动起来所占用的空间是很大的,极易与隧道壁发生碰撞.由于机械臂的质量大,运动惯性很大,碰撞产生的后果是极其严重的.对实际台车进行试验调试时,开始没有对末端杆件姿态进行约束,机械臂的末端杆件摆动很大;由于惯性、杆件及关节连接件的非绝对刚性、多个油缸同时运动时液压系统的不均匀性等原因,末端杆件的运动非常不平稳,效果很差.在本仿真中,选取右臂从30号孔到41号孔的运动过程来分析,仿真中忽略了机械臂的质量、弹性、阻尼及液压系统等动力学要素,仅在理想情况下考虑其运动学关系.30号孔的末端杆件的位姿数据为:位置坐标(-1 600,545,4 900)mm(参考坐标系见图2),姿态数据(0°,0°,0°),运动学反解后得到的5个转动关节数据(17.398°,-13.647°,85.772°,-16.891°,-14.275°).41号孔的末端杆件的位姿数据为:位置坐标(-400,3 425,4 900)mm(参考坐标系见图2),姿态数据(0°,-3°,0°),运动学反解后得到的5个转动关节数据(3.304°,36.546°,0.207°,-33.551°,-13.185°).在考虑末端杆件姿态约束时,关节1、2、3的角度均匀变化,关节4和5按照第2节式(10)和(12)跟随变化,保证末端杆件的姿态与工作断面垂直,仿真过程未考虑关节6的运动.仿真过程中末端杆件的运动过程如图8a所示,图8b所示为未对末端杆件姿态进行约束时的仿真结果,5个转动关节都假设为均匀变化.图8a、b的结果对比可见,考虑末端杆件姿态约束的机械臂运动过程,滑架的空间占用小,与隧道壁发生碰撞干涉的可能性小.如果考虑动力学因素的话,结果的对比将更为明显.
为了定量表示机械臂与隧道壁碰撞的可能,图9示出了仿真过程中末端杆件(滑架)与隧道壁之间的最短距离.图中A曲线表示运用约束机械臂末端姿态时的曲线,B曲线表示未约束机械臂末端姿态时的曲线.2条曲线对比明显,运用约束机械臂末端杆件姿态方法可以有效地减少滑架与环境发生碰撞的可能性.
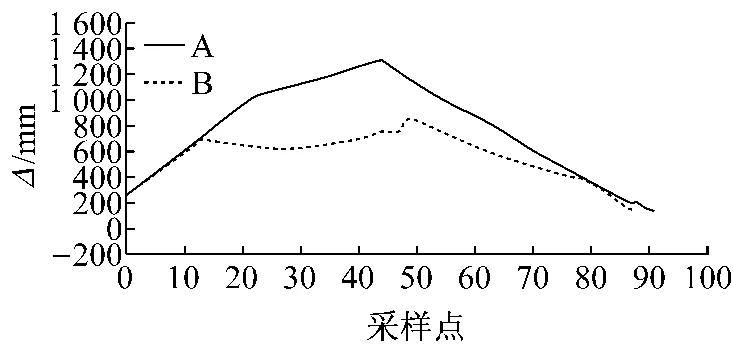
图9 滑架与隧道壁最短距离Fig.9 The shortest distance between sliding frame and tunnel walls
3.2.2 仿真2:连续多孔机械臂定位过程仿真
利用左右臂的连续运动过程仿真来分析机械臂杆件间的自干涉与互干涉情况.同样不考虑实际工作中2个臂的进度可能不同、液压系统的不对称等情况,按照图7所示的钻孔任务分配孔序,2个臂分别从各自的起始孔位,经过中间孔位,最后运动到终点孔位.2个臂的起始孔和终止孔的数据见表1.仿真过程与仿真1类似,前3个关节均匀变化,同时到达目标值,关节4和5按照式(10)和(12)进行垂直姿态时角度变化的跟踪.对于单臂的自干涉,仅可能发生在滑架与大臂之间,按照第3节公式计算最短距离,图10为单臂自干涉的仿真结果.
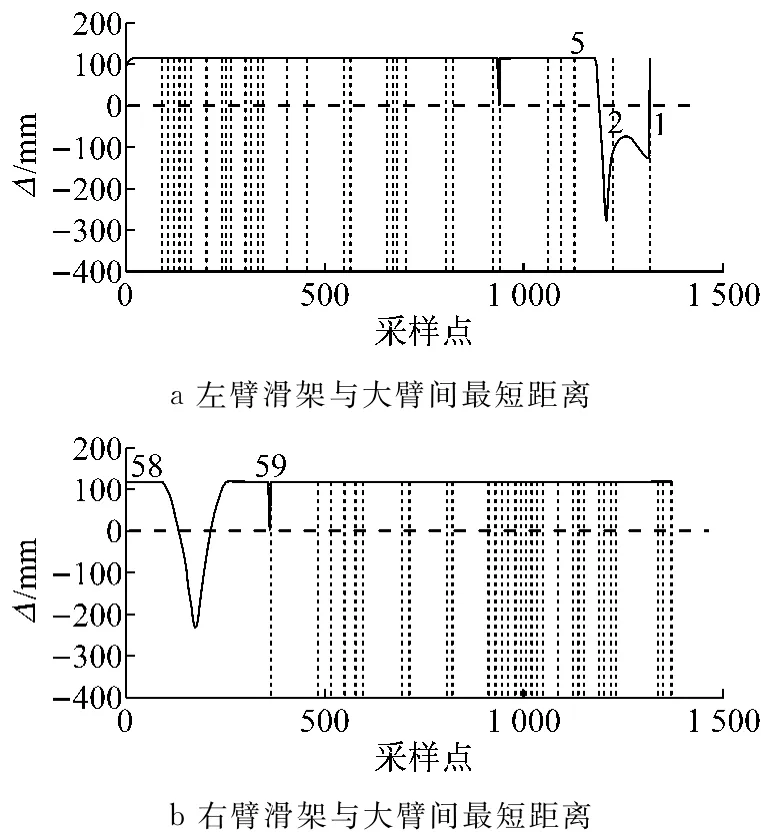
图10 机械臂滑架与大臂间最短距离(自干涉)Fig.10 The shortest distance between sliding frame andboom of the manipulator(self interference)

表1 2个臂的起始孔和终止孔数据Tab.1_Data of starting and ending holes of two manipulators
图10中横坐标为机械臂运动仿真过程的采样时间点,在曲线上标出了发生干涉前后的作业炮孔序号(钻臂按图7所示顺序移动),纵坐标为大臂与滑架的最短距离Δ,当Δ≤0时有自干涉发生.多数情况下大臂与滑架间最短距离为一固定值(未画出),该值就是图1关节5轴线上大臂端点与滑架固连的一小段垂直杆件的长度.只有当左臂(见图10a)从5号孔向2号孔、从2号孔向1号孔移动过程中会发生自干涉.当右臂(见图10b)从58号孔向59号孔移动过程中会发生自干涉.这与实际情况是相符的,因为此时机械臂出现如图4b所示的干涉情况,即滑架的后部已经与大臂紧靠在一起.要避免这种自干涉的发生,只需要对关节4的转动角度θ4进行一个极小值的限制即可,在实际控制中给定这个极小值角度为7°.
图11为两臂同时按图7给出的孔序运动时,2个臂之间的最短距离计算结果.由于凿岩台车机械结构的空间限制,2个机械臂的安装位置距离很近,在2个臂同时运动时,如不小心,机械臂间碰撞的可能性很大.采取本文提出的机械臂移动过程中保持末端杆件姿态垂直于工作断面的方法,能够有效地防止互干涉的发生.图11a显示机械臂运动过程中2个臂之间的最短距离基本大于200mm,只有某个点时,2个臂之间的最短距离小于100mm,总体无碰撞发生.图11b为机械臂移动过程中未采取末端杆件姿态垂直断面的方法,在2个臂移动过程中,多处发生碰撞.在实际情况下,机械臂凿岩任务完成的进度不同,发生互干涉的危险性更为严重.只对末端杆件姿态进行约束会减少干涉的可能性,但还不能完全避免干涉.实际控制时,在移动机械臂前,先利用本文第3.1节的方法,计算移动过程中的两臂间最短距离进行干涉预测,根据预测结果对钻孔顺序进行调整.此时可定义一个机械臂为主臂另一个为从臂,如有干涉的危险时,从臂避让主臂.运用这种策略,可以有效避免机械臂间发生互干涉的风险.
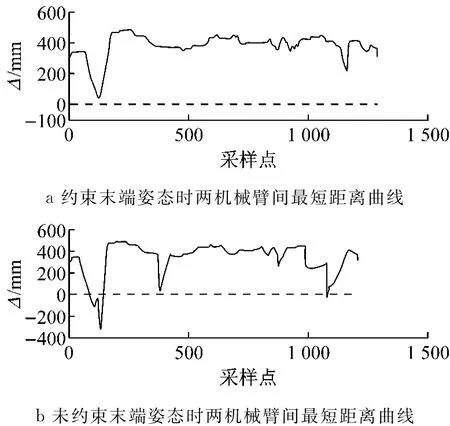
图11 两机械臂的互干涉情况Fig.11 Interference between two manipulators
图12为仿真过程中左臂滑架与隧道壁的最短距离计算结果.两图对比可以看出,采用约束机械臂末端杆件姿态垂直于工作断面的方法有效地避免了运动过程中机械臂与环境的干涉.

图12 机械臂与隧道壁间最短距离Fig.12 The shortest distance between manipulator and tunnel walls
4 结论
(1)考虑台车机械臂处在钻孔工位时,针对滑架偏离垂直断面的姿态方向一般不大这一实际情况,提出在移动过程中保持末端执行器(滑架)垂直于断面的位姿路径,等到机械臂基本到达目标位置后再将关节调整至目标姿态,即所谓的基于末端姿态约束的避障策略.这一策略通过文中的理论推导及仿真计算,证明是有效的.这种方法已经应用于某凿岩台车自动化改造中六自由度机械臂的实时控制.
(2)运用四元数方法对机械臂的运动关系进行描述与分析,推导出了关节4和5跟随前面3个关节的计算公式.
(3)针对空间杆件的干涉判断,提出3类9种距离的计算方法,得到杆件线段在空间的最短距离.运用这种方法,对某凿岩机械臂运动过程的干涉进行判断,运算结果可靠.
[1]Lahouar S,Zeghloul S,Romdhane L.Collision free path planning for multi-DoF manipulators[M]//Industrial Robotics:Theory,Modeling and Control.[S.l.]:Pro Literatur Verlag,2006:349-378.
[2]Lavalle S M.Planning algorithms[M].Cambridge,Eng.:Cambridge University Press,2006.
[3]Udupa S M.Collision detection and avoidance in computer controlled manipulators[D].Pasadena:California Institute of Technology,1977.
[4]Lozano-Pérez T,Wesley M A.An algorithm for planning collision-free paths among polyhedral obstacles[J].Communications of the ACM,1979,22(10):560.
[5]Tournassoud P,Planification et contrÔle en robotique:application aux robots mobiles et manipulateurs traite des no (French)[M].Paris:Hermes Science,1992.
[6]Khatib O.Real-time obstacle avoidance for manipulators and mobile robots[J].The International Journal of Robotics Research,1986,5(1):90.
[7]Newman W S.High-speed robot control in complex environments[D].Boston:Massachusetts Institute of Technology,1987.
[8]Wu J,Dick C,Westermann R.Efficient collision detection for composite finite element simulation of cuts in deformable bodies [J].The Visual Computer,2013,29(6):739
[9]Glondu L,Schvartzman S C,Marchal M,et al.Fast collision detection for fracturing rigid bodies[J].IEEE Transactions on Visualization and Computer Graphics,2014,20(1):30
[10]Mujika A,Oyarzun D,Arrieta A,et al.Real time accurate collision detection for virtual characters[C]//WSCG 2010 Communication Papers.Plzen:The Press of the University of West Bohemia,2010:123-130.
[11]Burdick J W.On the inverse kinematics of redundant manipulators:characterization of the self-motion manifolds [M]//Advanced Robotics.Beilin:Springer,1989:25-34.
[12]Oriolo G.Stabilization of self-motions in redundant robots [C]//Robotics and Automation,1994 IEEE International Conference on.[S.l.].IEEE,1994:704-709.
[13]王连圭,马保离.冗余机器人系统的自运动控制[J].控制与决策,2003,18(2):199.WANG Liangui,MA Baoli.Self-motion control of redundant manipulators[J].Control and Decision,2003,18(2):199.
[14]马保离.冗余机器人的双向自由运动路径规划[J].控制理论与应用,2005,22(4):547.MA Baoli.Bi-directional self-motion path planning of redundant manipulators[J].Control Theory &Applications,2005,22(4):547.
[15]Zhang Y,Zhu H,Tan Z,et al.Self-motion planning of redundant robot manipulators based on quadratic program and shown via PA10 example[C]//Systems and Control in Aerospace and Astronautics.[S.l.].IEEE,2008:1-6.
[16]Hamilton W R.Elements of quaternions(Vol.I &II)[M].New York:Chelsea,1869.
[17]Yang A T,Freudenstein F.Application of dual-number quaternion algebra to the analysis of spatial mechanisms[J].Journal of Applied Mechanics,1964,31(2):300.
[18]Gouasmi M.Robot kinematics,using dual Quaternions[J].IAES International Journal of Robotics and Automation(IJRA),2012,1(1):13.
[19]Sariyildiz E,Temeltas H.Solution of inverse kinematic problem for serial robot using dual quaterninons and plücker coordinates[C]//Advanced Intelligent Mechatronics,IEEE/ASME International Conference on.[S.l.]:IEEE,2009:338-343.
[20]张荣辉,贾宏光,陈涛,等.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程,2008,16(10):1963.ZHANG Ronghui,JIA Hongguang,CHEN Tao,et al.Attitude solution for strapdown inertial navigation system based on quaternion algprithm[J].Optics and Precision Engineering,2008,16(10):1963.
Collision Avoidance Based on Pose Constraint of End Link for Serial Manipulator
WANG Hengsheng1,2,HUANG Pinglun2,PENG Tianbo2
(1.State Key Laboratory for High Performance Complex Manufacturing,Central South University,Changsha 410083,China;2.College of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)
To reduce the possibility of motion interference of manipulators,apose constraint was proposed according to the mechanism characteristics of manipulators for a hydraulic tunneling rig with two 6-DoF(degree of freedom)manipulators.The pose constraint is that the end link of manipulator keeps perpendicular to working cross section during whole motion process.Then,kinematic methods for the realization of the constraint and the minimum distance between spatial links were given.Finally,motion simulation of manipulators was made for a tunneling cross section with 64-borehole design pattern.The results show that the pose constraint of end link perpendicular to working section during the motion of manipulators is effective for collision avoidance.
6-DoF(degree of freedom)manipulator;collision avoidance;motion interference;pose constraint
TP242.3
A
0253-374X(2016)01-0128-08
10.11908/j.issn.0253-374x.2016.01.019
2015-01-08
国家“九七三”重点基础研究发展计划(2013CB035504)
王恒升(1963—),男,教授,博士生导师,工学博士,主要研究方向为智能机器人.E-mail:whsheng@csu.edu.cn

