曲率半径对矮塔斜拉桥车桥耦合振动影响研究①

黎曙文，郭向荣，尹邦武

(1.中铁第四勘察设计院集团有限公司，湖北武汉430063; 2.中南大学土木工程学院，湖南长沙410075)

对于100 m以下的中小桥采用预应力箱梁结构形式的比较多，200 m以上采用一般的斜拉桥形式较为普遍，对100～200 m跨度的桥梁采用介于预应力箱梁和一般斜拉桥之间的桥梁形式比较合适，兼有梁桥和斜拉桥优点的矮塔斜拉桥是一种很好的选择［1－3］。矮塔斜拉桥相对于一般的梁桥具有自重和预应力钢筋数量较小的优点，相对一般斜拉桥而言，由于各索之间应力变化小，可显著降低塔高且更加经济，因而矮塔斜拉桥是一种具备实用价值的桥梁形式［2，4－5］。由于铁路桥梁时常为曲线布置，因而研究曲率半径对矮塔斜拉桥车桥耦合动力性能的影响具有实际意义。本文以某跨径布置为(88+148+88)m的塔梁固结形式矮塔斜拉桥为例，采用中南大学自编车桥耦合软件TBI，建立全桥有限元模型，对其自振特性及车－桥耦合振动响应进行了计算与分析，进而确定曲率半径对矮塔斜拉桥动力响应、车辆行车安全性及舒适性的影响。

1 工程概况

本文算例为一曲线矮塔斜拉桥，跨径为(88+ 148+88)m，总体布置如图1所示。采用塔梁固结体系，主塔采用左右分离独立式设置，同一截面处有并排2个柱式塔，每个主塔有6对拉索，全桥共24对拉索。中支点梁高7 m，端支点及跨中处梁高3.5 m。3号墩采用固定支座，其余3个墩为活动支座。

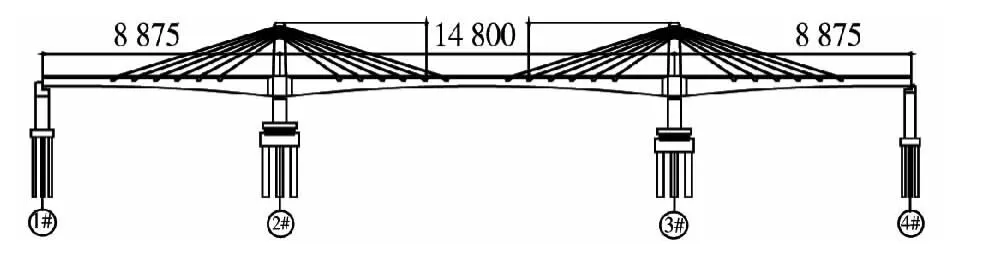
图1 桥梁结构总体布置图Fig.1 Overall arrangement of bridge structure

图2 主梁截面图Fig.2 Main girder cross－section

梁体采用单箱单室直腹板箱梁截面，斜拉索锚固于悬臂板上。主梁顶板宽10 m，底宽6.5 m，具体尺寸见图2所示。斜拉索采用双索面体系，梁上间距8.0 m，塔上间距0.7 m。索塔采用柱式塔，桥面以上塔高18.0 m，桥面以上塔的高跨比为1/8.2。塔柱为矩形实心截面，顺桥向以“上窄下宽”连续变化，顺桥向尺寸变化范围为 4.0～5.0 m，横桥向尺寸不变为2.0 m。桥梁的设计速度为120 km/h，单线行车。

2 曲线梁桥车－桥时变系统空间计算模型及其算法

相对直线梁桥，曲线梁桥车桥耦合振动分析的关键在于:合适的车辆模型;正确的曲线梁桥的振动理论以及快速的数值计算方法［6－7］。

2.1 车辆模型

客车及机车均为二系弹簧悬挂，假设车辆由车体、前后转向架及4个轮对共7个刚体组成。车体与前后转向架之间、转向架与各轮对之间均由线性弹簧和黏滞阻尼器相联，蠕滑力按线性考虑。轮对、转向架和车体沿桥跨作匀速运动，即不考虑机车、车辆纵向振动及其对桥梁振动及行车速度的影响。车体及转向架关于质心左右对称和前后对称。沿铅垂方向，轮对与钢轨密贴(密贴接触模型)，即轮对与钢轨的竖向位移相同［8］。

这样，车体空间振动有侧摆、侧滚、摇头、点头、浮沉等5个自由度;每个构架有侧摆、侧滚、摇头、点头、浮沉5个自由度;每个轮对有侧摆、摇头等2个自由度，故每辆四轴车辆共有23个自由度(见表1)。其位移参数列阵为:

表1 车辆模型的自由度表Table 1 Degrees of freedom of vehiclemodel

运用车辆动力学理论，即可得到车辆的运动方程:

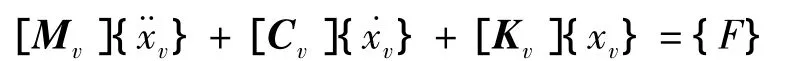
式中:［Mv］，［Cv］和［Kv］分别表示车辆的质量矩阵、阻尼矩阵和刚度矩阵。

2.2 桥梁模型

桥梁结构的自振特性与其车桥耦合振动密切相关，选择合适的计算模型来求解桥梁的自振频率和振型是进行车桥耦合分析的基础。对曲线梁桥而言，由于存在曲率，桥梁的截面主轴和作用的荷载通常不在一个平面内，因而其振动属于空间振动问题，需要选用空间梁单元(板单元)并采用以直代曲方式对结构进行离散。对空间梁单元而言，每个节点包含6个自由度——沿单元局部坐标系方向的3个线位移和绕3个坐标轴的转角位移;板单元采用4节点8自由度的矩形单元，则共有8个线位移自由度。

图3 正交流动坐标系Fig.3 Coordinates orthogonal flow system

为简便而正确地分析曲线梁桥，对整体结构采用如图3所示的正交流动坐标系，这样虽然在不同节点的坐标系不一定相同，但每个节点的坐标系都是唯一确定的，结构的内外力在各个节点上都是平衡的，这样处理可直接输出在局部坐标系下节点的响应值从而大大简化计算节约机时。

本桥主梁截面为箱梁，桥面系在计算时采用脊梁模型。它把桥面系的刚度(竖向、横向挠曲刚度、扭转刚度)和质量(平动质量和转动质量)都集中在中间节点上，节点和拉索之间采用刚臂连接。斜拉索采用空间杆单元建模，对于动力分析而言，垂度对弹性模量的影响可以忽略不计，故本文模型中弹性模量采用预应力索材料的弹性模量，不进行折减［5］，而作为线弹性单元处理;斜拉索的初始拉力以荷载的形式加到相对应的杆单元上，转化为初始刚度矩阵，进而加到主刚度矩阵上。主塔采用三维梁单元模拟，由于单元划分的粗细决定了堆聚质量的分布、振型的形状等，所以单元划分不宜太粗，否则将导致频率降低、塔根弯矩减小。桩基础处理采用桩基模型，通过三维梁单元模拟实际桩基础，同时桩－土共同作用则采用m法模拟。模型共划分为3 047个节点，5 062个单元，其有限元模型如图4所示。所有构件之弹性模量E和泊松比μ按现行铁路桥梁规范取值，铁路桥面二恒取90.18 KN/m。该桥采用塔梁固结体系，因此桥塔与主梁采用主从约束的形式进行刚接，从而形成一个整体与桥墩进行连接，主梁与边墩则放松纵向的水平平动自由度。

计算法获得烃露点通过现场获取实际天然气样品，然后采用气相色谱法分析天然气的组成，再由天然气组成数据通过软件计算天然气的烃露点。由于天然气是一种组分十分复杂的混合物，影响计算法获得烃露点结果的因素较多，其主要影响因素包括样品的代表性、组成分析结果的准确性以及计算模型的选择等。

图4 桥梁有限元分析模型Fig.4 Finite elementmodel of the bridge

在进行动力计算时，可采用一致质量和集中质量矩阵2种方法，其中集中质量矩阵是对角矩阵。按一致质量矩阵计算时，结构频率值稍微偏高且计算繁琐;而按集中质量矩阵考虑时，不仅质量矩阵得到简化，而且得到的结构频率值有时比一致质量矩阵求得值更能与实测值吻合。因此在实际计算结构动力特性时，通常采用集中质量矩阵。

采用Rayleigh阻尼来描述结构体系的阻尼特性，可得到桥梁系统的运动方程:

式中:［MB］，［CB］和［KB］分别表示桥梁系统的质量矩阵、阻尼矩阵和刚度矩阵。

2.3 列车－桥梁时变系统振动方程的建立与求解

车－桥耦合系统为相当复杂的时变系统，宜采用能量原理计算。将桥上列车与桥梁视为整体振动系统，分别计算任意时刻t桥梁空间振动总势能∏b(t)及桥上车辆空间振动总势能∏v(t)，在∏v(t)中考虑车辆与桥梁之间的相互作用。二者相加可得到弹性系统总势能∏d(t)，由动力学势能驻值原理 δ∏d=0及形成矩阵的“对号入座”法则［7，10－11］，可以得出t时刻列车－桥梁系统的质量矩阵［M］、阻尼矩阵［C］、刚度矩阵［K］及荷载列阵［P］，从而列出在t时刻列车桥梁时变系统空间振动的矩阵方程:

式中:{¨x}，{˙x}和{x}分别表示车桥系统在t时刻的加速度、速度、位移参数列阵。该系统的刚度、质量、阻尼矩阵随列车的运行而发生变化。矩阵方程式(1)只考虑了车辆重力作用，还须将激励源作为已知参量代入上述矩阵方程进行矩阵分块。根据文献［8］，以构架实测蛇形波(确定性分析)、构架人工蛇形波(随机性分析)作为横向振动激励源，轨道竖向几何不平顺作为竖向激励源。这样，方程式(1)的振动位移参数{x}可分为k个已知参数和n个未知参数，即{x}可写成［xkxn］T。则式(1)可重新组成:

式(2)右边各项都已知，因而它是具有自由项的车—桥系统空间振动微分方程组。TBI软件独创性地调用了一种用wilson－θ法高效求解矩阵方程组(2)的求解器，采用一种特殊的一维变带宽反序存贮及矩阵反序分块消元的技巧，大大提高了车桥耦合振动计算过程中的运算效率［8－10］。

3 计算结果分析

为考察曲率半径对结构车桥耦合分析的影响，分别计算了曲率半径为700～4 000 m、直线共16种工况下的动力特性。为了更好反映曲率半径对该桥动力特性的影响，对模型有以下基本假定: (1)截面尺寸、跨径布置及约束条件均保持不变;(2)列车以相同的速度通过不同曲率半径的矮塔斜拉桥。

在车桥耦合分析时，对国产CRH2型车以120 km/h单线通过桥梁时的动力响应进行了仿真计算与分析研究。对比分析不同曲率半径桥梁的竖向与横向位移、车辆竖向与横向加速度、轮对最大横向力、轮对脱轨系数、轮重减载率等。计算中轨道不平顺函数采用了德国低干扰谱。

3.1 自振特性分析

桥梁的自振频率及振型特点反映了桥梁的刚度及桥梁的动力特性，是车桥振动响应分析的基础。采用上述桥梁动力计算模型，利用子空间迭代法对该矮塔斜拉桥各个半径下的自振特性进行了计算分析，第一阶横向、纵向、竖向振型对比结果如表2所示。

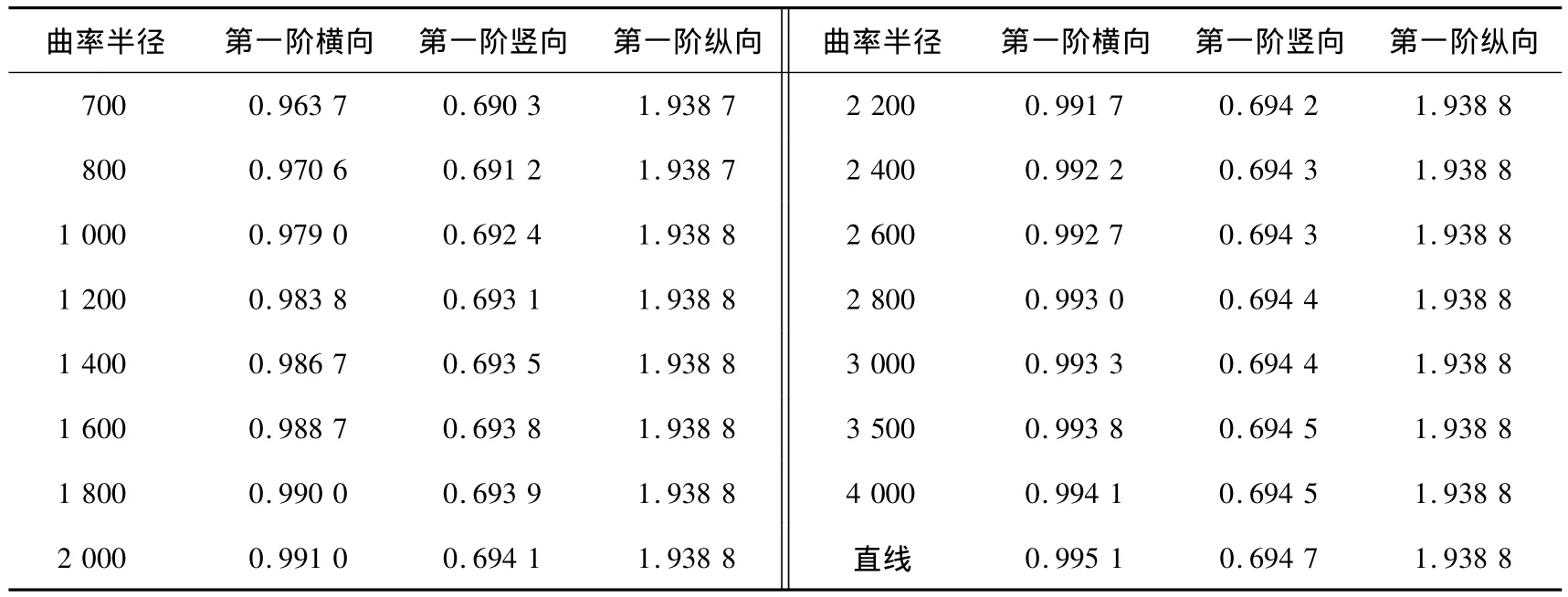
表2 不同曲率半径主要振型对比表Table 2 Comparison of frequency and vibration of different radius of curvatures

3.2 桥梁动力响应

图5和图6分别为CRH2列车以100，130，160，180和200 km/h 5种速度通过不同曲率半径桥梁时桥梁横竖向位移的最大值。图中振动位移均为相对于初始平衡位置而言。图7和图8所示分别为CRH2列车以120 km/h时速通过曲率半径1 000m的矮塔斜拉桥桥时中跨跨中横向位移时程曲线及中跨跨中竖向位移时程曲线。

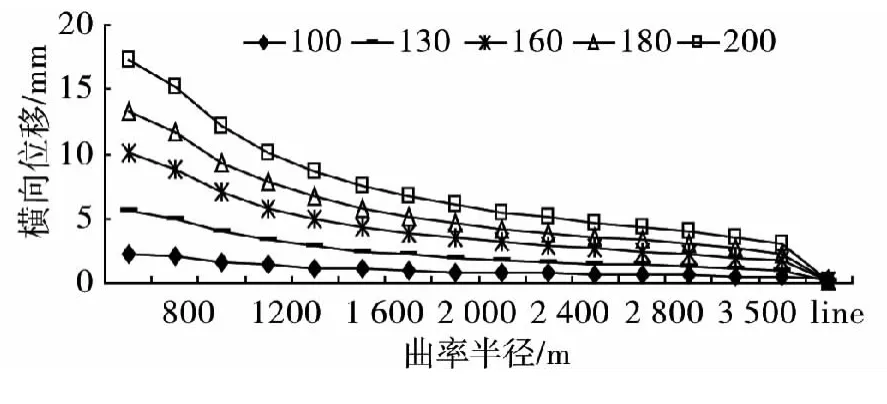
图5 中跨跨中横向位移极值随曲率半径变化趋势Fig.5 Changes of lateral displacement with different radius of curvatures on themid－span

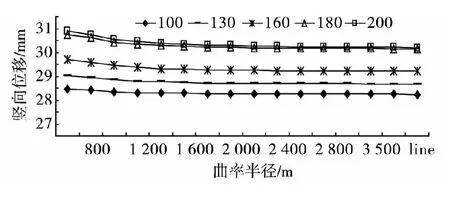
图6 中跨跨中竖向位移极值随曲率半径变化趋势Fig.6 Changes of vertical displacementwith different radius of curvatures on themid－span

由图5可知:中跨跨中横向位移随着曲率半径的增大而减小，车速越大，曲率半径的影响越显著。当半径为700 m时，横向位移达到最大;当半径为无穷大即桥梁为直桥时，横向位移达到最小。

由图6可知:中跨跨中竖向位移随曲率半径的增大而减小，曲率半径的影响不显著。当曲率半径为700时，竖向位移达到最大，当桥梁为直桥时，竖向位移为达到最小。当曲率半径超过2 000 m后，竖向位移随曲率半径变化较为平缓。说明曲率半径对列车的横竖向响应都有影响，但是曲率半径对横向位移的影响非常显著，对竖向位移的影响相对较小。

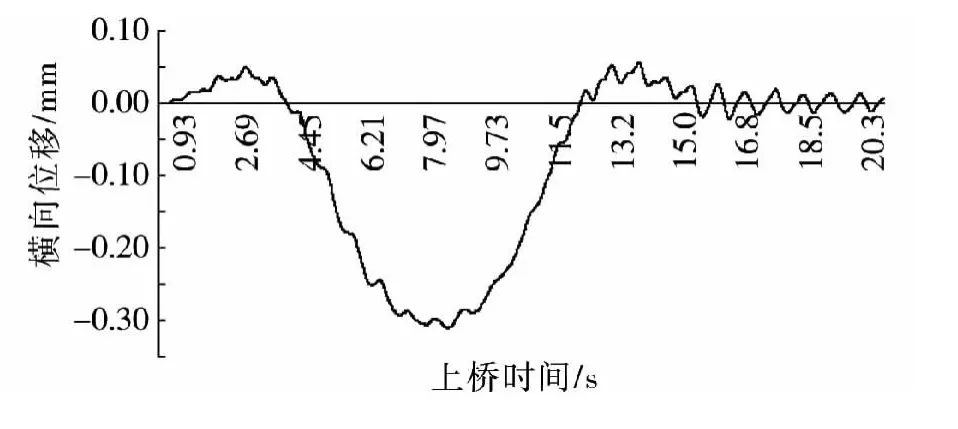
图7 中跨跨中横向位移极值时程曲线图Fig.7 Time history of lateral displacement curve on themid－span(120 km/h)

图8 中跨跨中竖向位移极值时程曲线Fig.8 Time history of vertical displacement curve on themid－span(120 km/h)

3.3 列车动力响应

图9～图11为CRH2列车以100，130，160，180和200 km/h 5种速度通过不同曲率半径桥梁时车辆脱轨系数、轮重减载率及横向力的变化趋势。

由图9可知:脱轨系数随曲率半径的增大而减小，车速越大，受曲率半径的影响越明显。当车速小于180 km/h时，脱轨系数较小，且受曲率半径变化的影响小，当车速大于180 km/h时，脱轨系数明显增大，此时曲率半径的影响相当显著，当曲率半径超过1 000 m时，脱轨系数随着曲率半径的增大基本保持不变;本桥的曲线超高按120 km/h的时速设置，从图10可知当车速接近120 km/h时，轮重减载率基本不受曲率半径的影响。当车速明显超出120 km/h时，轮重减载率受曲率半径的影响变得显著，曲率半径小于2 400 m时，轮重减载率随曲率半径的增大而明显减，当曲率半径大于2 400 m时，轮重减载率随曲率半径变化趋于平缓;从图11可以看出，横向力在曲率半径小于1 600 m时随着曲率半径的增大而显著减小，当曲率半径大于1 600 m时，横向力基本不受曲率半径的影响。

图9 脱轨系数随曲率半径变化Fig.9 Changes of derailment coefficient with different radius of curvatures

图10 轮重减载率随曲率半径变化Fig.10 Changes ofwheel load reducing rate with different radius of curvatures

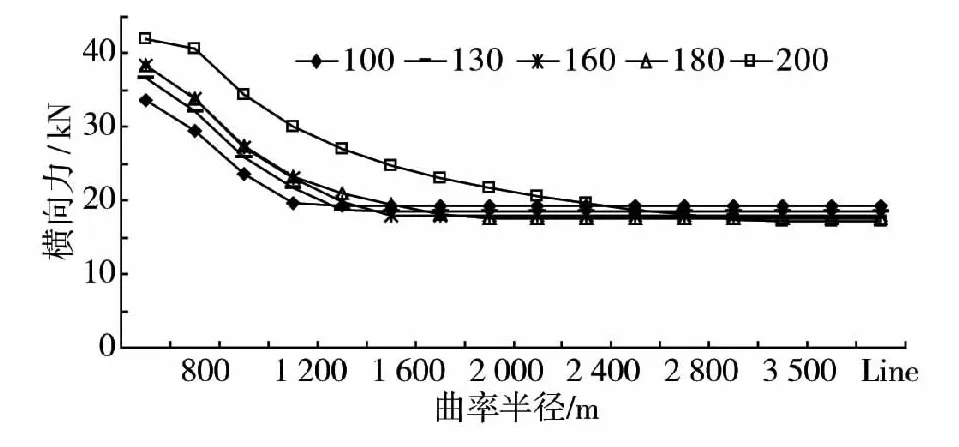
图11 横向力随曲率半径变化Fig.11 Changes of lateral force with different radius of curvatures

本桥的设计半径为1 000 m，在设计速度下桥梁的横向位移为3.1mm，竖向位移为28.71mm;列车的脱轨系数为0.52，轮重减载率为0.41，满足规范［11－12］的要求。同时桥梁、列车的其他评价指标均满足规范要求。

4 结论

(1)曲率半径对矮塔斜拉桥的横竖向频率有一定影响，随着曲率半径的增大，第一阶纵向频率变化不明显，第一阶横向、竖向频率逐渐增大，且横向频率敏感程度大于竖向频率。从计算分析还可得知该斜拉－连续梁桥振型表现出明显的三维性和相互耦合性，墩、塔、梁的振动相互影响。

(2)桥梁系统动力响应随曲率半径的减小而增加。跨中横向位移受曲率半径影响显著，且车速越大，受曲率半径影响越明显。跨中竖向位移受曲率半径影响较小。且当曲率半径大于某一特定值后，竖向位移基本不受曲率半径的影响。

(3)列车系统动力响应的各项指标随曲率半径的变化呈现出不同的变化趋势。脱轨系数在车速很小时基本不受曲率半径的影响，随着车速增大，脱轨系数受曲率半径影响变得非常显著，伴随着曲率半径的增大，脱轨系数明显减小，当曲率半径达到一个特定值后，脱轨系数基本上不受曲率半径影响;轮重减载率在车速为平衡超高对应的平衡速度时达到较小值，当车速大于平衡车速时，轮重减载率受曲率半径影响变化显著，随着曲率半径的增大轮重减载率明显减小，当曲率半径大于某一特定值时轮重减载率基本不受曲率半径的影响;横向力在曲率半径小于某一特定值时随曲率半径的增加会明显减小，而当曲率半径大于该特定值之后，横向力基本维持稳定，不再受曲率半径的影响。

［1］刘士林，王似舜.斜拉桥设计［M］.北京:人民交通出版社，2006.LIU Shilin，WANG Sishun.Design of cable－stayed bridge［M］.Beijing:China Communications Press，2006

［2］罗晓媛.地震作用下矮塔斜拉桥的车桥耦合振动研究［D］.长沙:中南大学，2009 LUO Xiaoyuan.Study on vehicle－bridge coupling vibration of the low tower cable－stayed bridge under earth-quake［D］.Changsha:Central South University，2009.

［3］陈从春，周海智，肖汝诚.矮塔斜拉桥研究的新进展［J］.世界桥梁，2006(1):70－73.CHEN Congchun，ZHOU Haizhi，XIAO Rucheng.The new research progress of low tower cable－stayed bridge［J］.The World Bridge，2006(1):70－73.

［4］何新平.矮塔斜拉桥的设计［J］.公路交通科技，2004 (4):66－68.HE Xinping.Design of low tower cable!stayed bridge［J］.Journal of Hihgway and Transportation Research and Development，2004(4):66－68.

［5］尹邦武，苗永抗，郭向荣.斜拉－连续刚构组合梁桥车－桥耦合动力响应分析［J］.铁道科学与工程学报，2013，10(2):11－16.YIN Bangwu，MIAO Yongkang，GUO Xiangrong.The vehicle－bridge coupling dynamic analysis of cable－stayed and continuous rigid－frame composite beam bridge［J］.Journal of Railway Science and Engineering，2013，10 (2):11－16.

［6］单德山.高速铁路曲线梁桥车桥耦合振动分析及大跨度曲线梁桥设计研究［D］.成都:西南交通大学，1999.SHAN Deshan.The vehicle－bridge coupling dynamic analysis of curved beam bridge for high speed railway and the design and research for long－span curve beam bridge［D］.Chengdu:Southwest Jiaotong University，1999.

［7］单德山，李乔.曲率半径对曲线连续梁桥车桥耦合振动的影响［J］.桥梁建设，2004(6):1－3.SHAN Deshan，LIQiao.Effect of curvature radii on vehicle－bridge coupled vibration about continuous curved girder bridges［J］.Bridge Construction，2004(6):1－3.

［8］曾庆元，郭向荣.列车桥梁时变系统振动分析理论与应用［M］.北京:中国铁道出版社，1999.ZENG Qingyuan，GUO Xiangrong.Theory and application of train－bridge time－variant system vibration analysis［M］.Beijing:China Railway Press，1999.

［9］曾庆元.弹性系统动力学总势能不变值原理［J］.华中理工大学学报，2000，28(1):1－3.ZENG Qingyuan.The principle of total potential energy with stationary value in elastic system dynamics［J］.Journal of Huazhong University of Science and Technology，2000，28(1):1－3.

［10］翟婉明，夏禾.列车－轨道－桥梁动力相互作用理论与工程应用［M］.北京:科学出版社，2011.ZHAIWanming，XIA He.Train－track－bridge dynamic interaction:theory and engineering application［M］.Beijing:Science Press，2011

［11］TB/T2360—1993，铁道机车动力学性能试验鉴定方法及评定标准［S］.TB/T2360—1993，Railway locomotives－specification for evaluation the dynamic performance and accreditation test［S］.

［12］GB/T5599—1985，铁道车辆动力学性能评定和试验鉴定规范［S］.GB/T5599—1985，Railway vehicles－specification for e－valuation the dynamic performance and accreditation test［S］.