基于并联的非接触平面运动测量传感器设计及其误差分析

徐志刚，白鑫林，王军义，王　昊

(1．中国科学院沈阳自动化研究所，辽宁沈阳　110016；2．中国科学院大学，北京　100039)

0　引言

目前，航天器平面运动测量多采用惯性导航陀螺及视觉等测量方式来实现[1]，但是陀螺以及视觉测量装置测量频率较低，无法用于闭环反馈控制。现开发的测量频率较高的平面运动测量系统多为利用角度测量装置以及距离测量装置通过机构组合而构成的接触式测量系统，在一些运动精度要求较高，且不允许有运动干扰的系统中，测量系统自身机构的运动会给被测系统运动带来影响[2]，因此迫切要求一种新型的非接触式平面运动测量装置。

针对这一情况，文中提出一种新型非接触式并联平面激光测距传感器，通过组合测量与计算求解，得到模样件的位姿信息。激光测距传感器具有较高的测量精度[7]，但是影响总体精度的因素也有很多[3]，对主要的8个影响因素，用蒙特卡洛法进行了相同概率分布下的随机抽样，并根据所建立的误差数学模型，得到被测量误差的概率分布情况。最后以某一实际待测情况为例，用蒙特卡洛法进行了相同概率分布下的随机抽样，并根据所建立的误差数学模型，得到被测量误差的概率分布情况。

1　传感器测量原理与安装标定

1．1基本结构与测量原理

非接触式平面激光测距传感器由3个相同的激光测距传感器、安装基座和被测对象组成，如图1所示。

其测量原理为3个相同的非接触式激光测距传感器测量相对于安装基准的距离值，通过对所获测量数据的组合算法，从而实现对物体平面运动两个方向相对位移的测量及绕Z轴转动角度的测量。非接触式激光测距传感器测量频率较高，能满足系统闭环控制的要求。

1．2传感器安装与标定

安装基座上安装3个相同的非接触式激光测距传感器，即在X轴方向安装2个，在Y轴方向安装一个，而安装基座位于在模样件相互垂直的相邻侧面上。

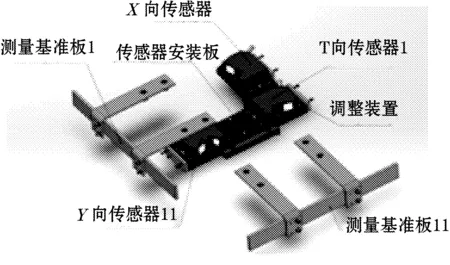
图1　非接触式并联平面激光测距传感器结构

标定方法：模样件的安装面经过精密加工，其垂直度误差很小，可以忽略不计。设在X、Y轴方向上的2个激光测距传感器的初始测量值分别为：y01、y02、x01，Y向传感器测量理论值为x02。在该传感器测量前，需要进行调整，直到满足下式：

y01=y02，x01=x02

2　测量对象数学模型建立

设被测量为G，则其与输入量之间的函数关系为：

G=f(x1，x2，l1，l2，l3，y1，|o1o2|，θ，t)

式中：l1、l2、l3为激光测距传感器测量值；x1、x2、y1为与激光测距传感器安装位置相关的参数；|o1o2|、θ1为与模样件质心相关的参数；t为环境温度。

由于环境温度变化不大，且对被测量G的影响较小，忽略其影响[4]，因此，G=f(x1，x2，l1，l2，l3，y1，|o1o2|，θ1)。

测量X、Y轴方向传感器安装点位置坐标分别为：a1(x1，0)、a2(x2，0)、b(0，y1)，则被测物体上传感器的坐标分别为：

u(x1，l1)，v(x2，l2)，w(l3，y1)

根据图2中三点坐标及几何关系o2o3⊥o2o4，得到直线o2o3、o2o4的方程分别为：

解上面的方程组得交点o2的x、y坐标为：

由交点o2的坐标、被测对象上任一点o1到o2的距离|o1o2|、直线o1o2与直线o2o3间的夹角θ1，可求得被测物体相对于安装基座及激光测距传感器X向、Y向位移和绕Z轴的转动运动参数如下。

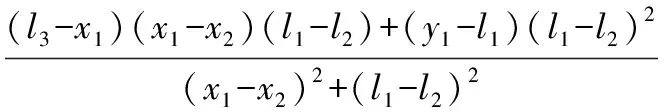
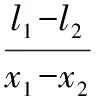
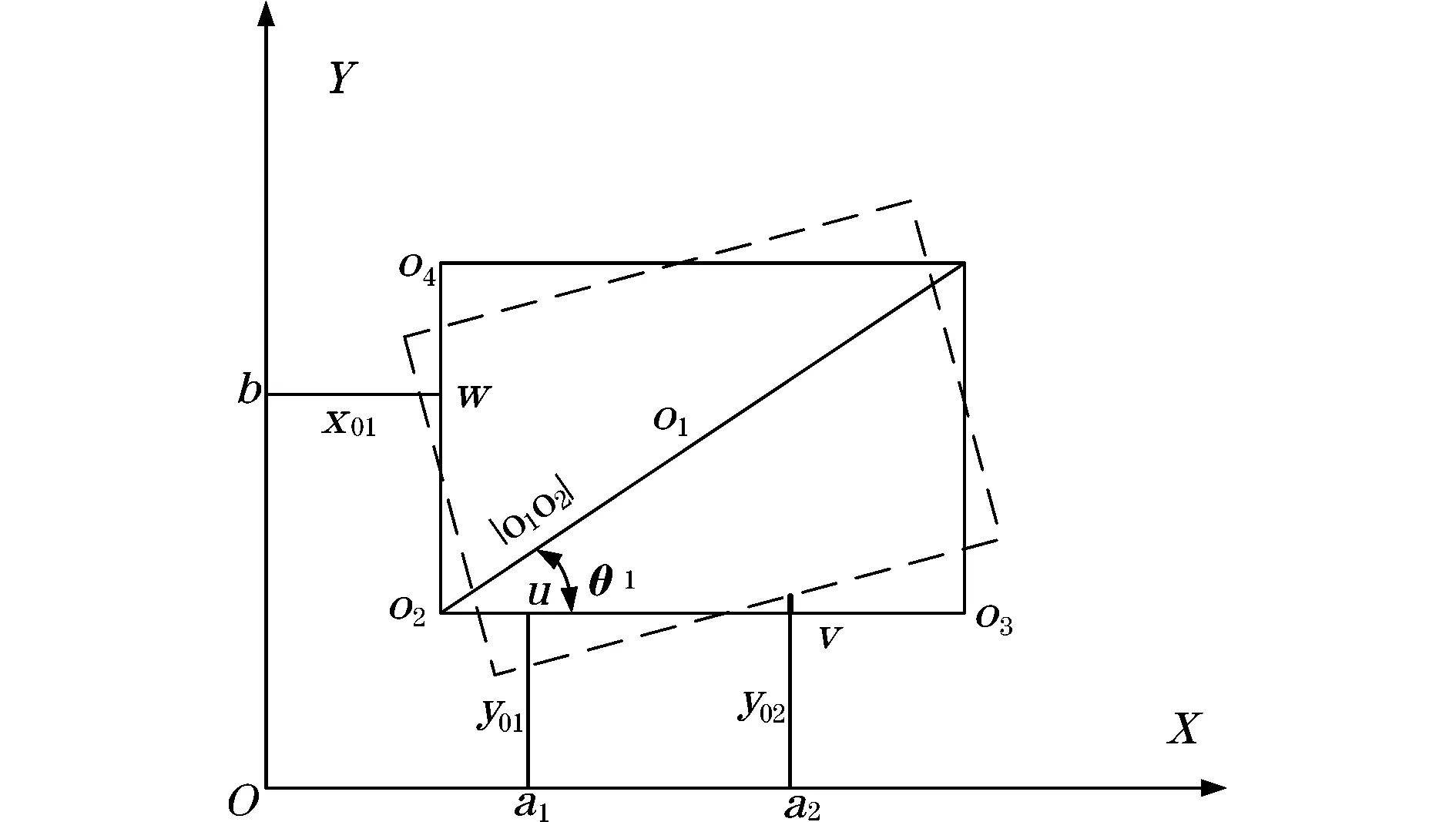
图2　测量原理图

3　误差分析

在不考虑温度变化、模样件安装面及测量基准板直线度等因素对被测量的影响下，用全微分法建立被测量误差的数学模型[5]，并用蒙特卡洛法对测量误差进行了定量分析。

3．1误差数学模型建立

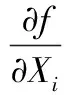
由于被测物体是三自由度的平面运动，故激光测距带来的测量误差由三部分组成，分别是：X、Y向位移误差ΔX、ΔY、绕Z向的转角误差Δθ，误差矩阵为：

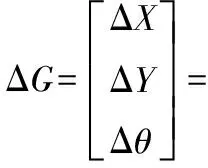
3．2测量误差蒙特卡洛法模拟

误差的蒙特卡洛模拟，就是在计算机对具有不同分布的误差随机量进行抽样，再按测量误差的数学模型算出大量的抽样数据，最终借助统计分析定量的获取测量误差的分布规律的一种方式[6]。

3．2．1伪随机数生成

生成(0，1)之间均匀分布的伪随机数的算法主要有：线性同余(MLCG)法、移位寄存器(或Tausworthe)法、Fibonacci法和混合法，这里使用线性同余法。

线性同余法由D．H．Lehmer提出，其基本形式是对任意整数X0，由以下公式确定：

X1=(aXi-1+c)modM

ξi=Xi/M，i=1，2，…

式中：乘子a为小于模M的正整数；c为非负整数，常选为零；ξ为伪随机数。

当c=0时，称为乘同余法，其满周期为：T=M-1。有研究表明，乘同余法优于加同余法，而混合同余法与简单的乘同余法相比并无显著优点[6]。目前，具有参数为M=231-1，以及a=16 807或630 360 016的乘同余方法得到广泛应用。

3．2．2伪随机数的随机性检验

伪随机数序列的随机性检验，就是按照从(0，1)上均匀分布随机所应具有的性质和规律，来研究所产生的伪随机数序列是否与这些性质和规律相符合。

伪随机数通过的检验越多，说明其越可靠。这里对所产生的伪随机数用矩检验法进行参数检验，用χ2检验法检验伪随机数的均匀性，用游程检验法检验伪随机数的独立性。

3．2．3随机变量抽样

随机变量的抽样是为了生成与原始误差有相同概率分布和统计特征的随机变量的抽样值。由于G=f(x1，x2，l1，l2，l3，y1，|o1o2|，θ1)的输入参数之间是独立的，由于各随机变量在有限区间都有上界，因此可以用简单分布的舍选抽样方法。具有概率密度f0(x)的随机变量x∈(m，n)的抽样公式为：

式中：η1、η2为(0，1)上的伪随机数；fmax为f0(x)的最大值。

对f0(x)的舍选抽样方法的流程图如图3所示。

图3　抽样流程图

3．2．4算例误差的数值计算

若某激光测距传感器的最小采样时间为：20 μs，位移分辨率为：1 μm，重复精度为：+2 μm，其安装精度为：0．02 mm，则对于如下输入参数：

u(520.000±0.01，342.019±0.002)(mm)

v(680.000±0.01，416.629±0.002)(mm)

w(379.324±0.002，600.000±0.01)(mm)

|o1o2|=(283.285±0.005)(mm)，θ1=45.00°±0.01°

用乘同余法生成(0，1)区间的伪随机数，并对伪随机数进行检验，伪随机数的检验结果见表1，从表中可以看出所产生的10 000个伪随机数满足随机性、均匀性、独立性要求。

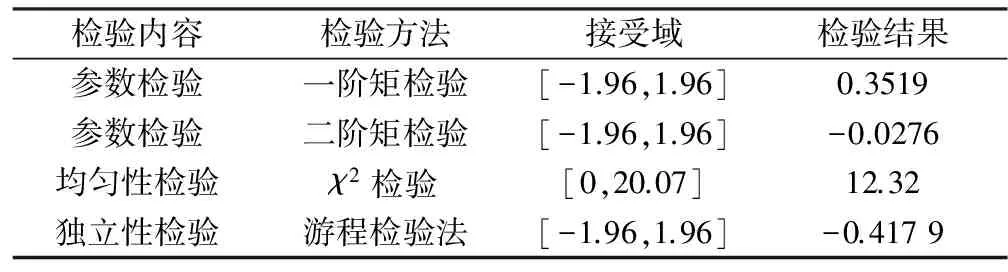
表1　伪随机数检验结果

图4　X向位移测量误差分布

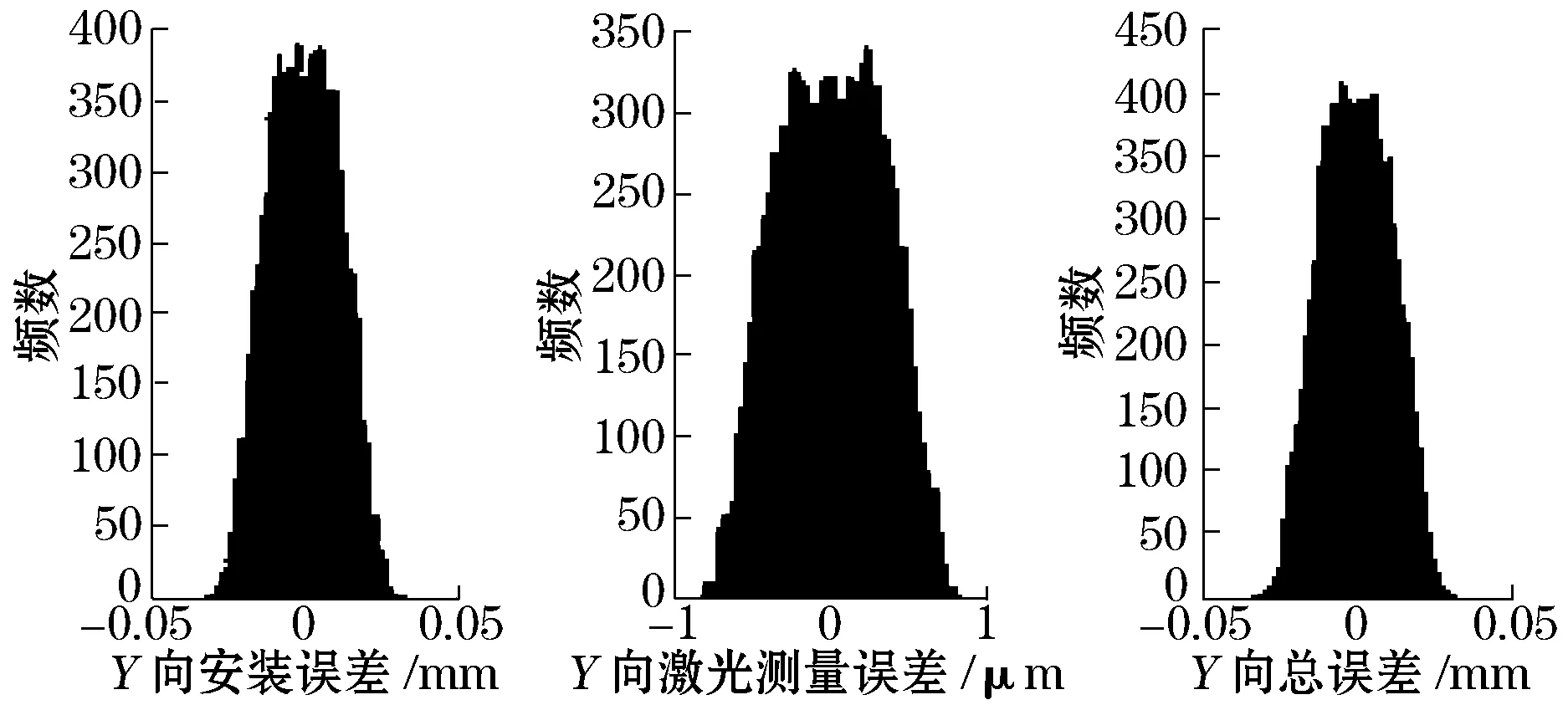
图5　Y向位移测量误差分布

图6　Δθ的误差分布

4　结束语

文中提出了一种基于并联的新型非接触式平面激光测距传感器，通过组合算法，能够测量出平面运动物体平移和转动量，实现了物体平面运动的非接触式测量。采用蒙特卡洛方法模拟出这种新型传感器平移和转动误差的概率分布，得到X、Y向测量精度分别高于±0.056 mm、±0.029 5 mm，转动精度高于5.6×10-3°，为这种传感器的实际应用提供了依据。

参考文献：

[1]姜春英，房立金，徐志刚，等．一种平面运动位姿组合测量方法研究．机械工程学报，2006，17(4)：362-366．

[2]王志乾，谢幕君，乔彦峰．一种非接触式测量方法的研究．光学技术，2003，7(4)：431-433．

[3]罗相杰，段纯刚，胡双启，等．某军用三坐标激光测量系统的安全性及精度控制方法研究．激光杂志，2006，27(3)：18-20．

[4]BAROUDI，DJEBAR，THIBERT．An instrumented structure to measure avalanche impact pressure：Error analysis from Monte Carlo simulations．EI．Cold Regions Science and Technology，2009，59(2)，242-250．

[5]费业泰．误差理论与数据处理．北京：中国机械工业出版社，2010．

[6]徐钟济．蒙特卡罗方法．上海：上海科学技术出版社，1985-06-ISBN．

[7]Haima YANG，Ruiting LI，Qingzhong WEI，et al．The study of high accuracy capacitive displacement sensor used in non-contact precision displacement measurement．The Ninth International Conference on Electronic Measurement & Instruments，Bei jing，2009．