光纤束强度调制传感器的性能优化研究

钟丽琼，胡　浩

(1．贵州大学机械工程学院，贵州贵阳　550025；2．贵阳学院机械工程学院，贵州贵阳　550003)

0　引言

反射式强度调制光纤传感器(RIM-FOS)是一种能广泛应用的传感器，得到了许多学者的研究[1-8]。在这类传感器的应用中，对微弱光强信号的采集一直都备受关注，因为接收到的光强信号的强弱直接影响着传感器的检测灵敏度，甚至决定了该类传感器是否能够满足检测要求，所以这也是制约该类传感器发展的关键因素之一。那么，为了增大接收光信号的功率，很多情况下采用了多根光纤集合成束的结构作为光的传输通道。

现今，光纤束的种类主要有同轴型、随机型、半圆型、同轴随机型、半圆随机型等，其中同轴型光纤束又是目前应用最为广泛的一种[9-10]。虽然通过同轴型光纤束的使用，提高了传感器的灵敏度，但是却没有人应用优化理论对此类光纤束的结构进行优化研究，从而能进一步提高其使用性能。正是在这一背景下，文中提出了利用约束非线性优化方法，对光纤束的结构进行优化，使其在应用中具有更好的传感性能，同时使得光纤束尺寸更加紧凑，价格更加低廉，最终实现性价比最优的同轴型光纤束结构。

1　优化模型建立

建立数学模型是优化设计实现的关键，也是优化设计过程中最困难的环节。建立模型时，需要考虑设计变量为那些参数，变量的约束条件是什么，优化需要实现什么目标函数等。

那么在同轴型光纤束的结构优化中，其设计变量包括输入光纤TF半径r1、接收光纤RF半径r2、TF与RF的间距l、两相邻TF之间的间距2h等多个变量。通过向量形式可表示为：

(1)

现在分析目标函数及约束条件，文中优化设计的目标是使接收光纤能够耦合更多的反射光，从而提高传感器的灵敏度，即使其强度调制函数M具有更大的峰值，如图1所示，假设多模光纤的出射光场强度分布均匀，那么调制函数M可简化表示为：

(2)

式中：S0表示RF端面的有效接收面积，图1中①、②种情况S0=S；S1表示反射光锥端面面积；μ为综合损失系数。

图1　光纤反射光锥与RF位置关系示意图

不难得出，反射光锥端面边界与接收光纤外边界相切时，强度调制函数M出现峰值。所以目标函数可表示为：

(3)

式中：Sgx为n条接收光纤端面的最大接收面积；Sgz为反射光锥端面边界与接收光纤外边界相切时，光斑的面积。

(4)

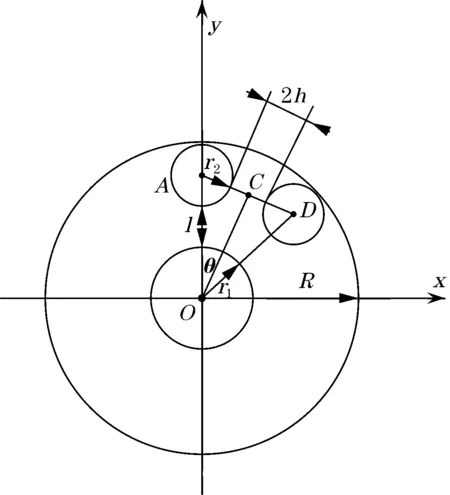
图2　光纤分布结构简图

再分析设计变量的边界条件为(优化设计中为了使光源耦合进入TF的光功率更高，使TF传送更大的光强度，直接选用尺寸参数较大的多模光纤作为入射光纤r1=50 μm，而常用的多模光纤最小半径为25 μm)：

(5)

把式(4)、式(5)整理为优化设计数学模型的标准形式为：

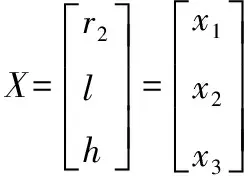
目标函数：

(6)

2　最优解探寻

文中建立的光纤束优化数学模型为具有约束的非线性规划问题，文中采用约束随机方向搜索法对其进行求解。按照上述求解方法，文中利用计算机对前述式(6)的数学模型进行了计算，得到使目标函数取得最小值时，设计变量X=(x1，x2，x3)的取值大小：x1=r2=25.001 0，x2=l=0，x3=h=0

根据上述的优化设计计算结果，可以看出在光纤束设计时，要使传感器的灵敏度越高，即要使传感器的强度调制函数M的峰值越大，此时接收光纤应该选用较小纤芯直径的多模光纤，并且入射光纤与接收光纤的间距l，以及接收光纤之间的间距2h要越小。

3　实验论证与分析

3．1仿真实验

文中首先利用仿真实验对同轴型光纤束优化设计结果进行论证。根据上述优化结果，首先分别取r1=50、r2=25，此时要使传感器灵敏度越高，则最好有l=0、h=0，通过计算设计了如表1尺寸参数的光纤束结构。表1中，当l=0时，TF外的RF根数最多为n1=9，此时某两根光纤之间存在h=2.92的间距；当h=0时，TF外的RF根数n2=10，但此时TF与RF之间存在l=5.906的间距(如图3所示)。

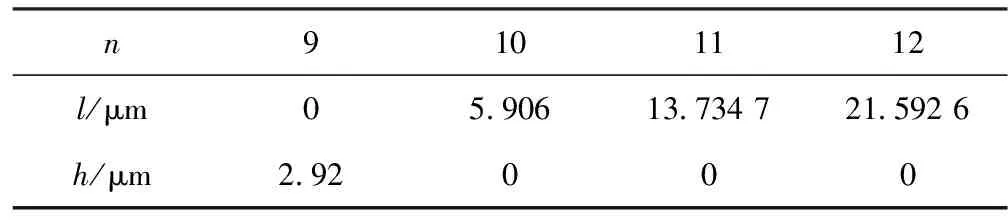
表1　不同接收光纤数对应尺寸

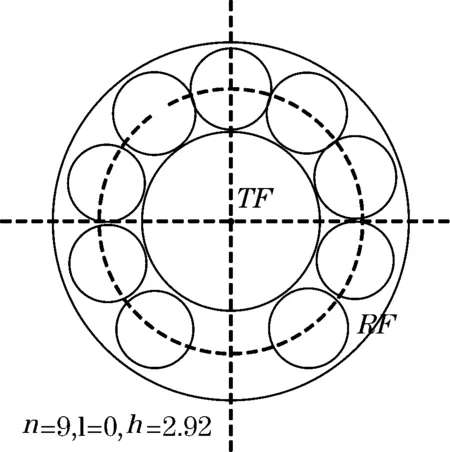
(a)n=9光纤束

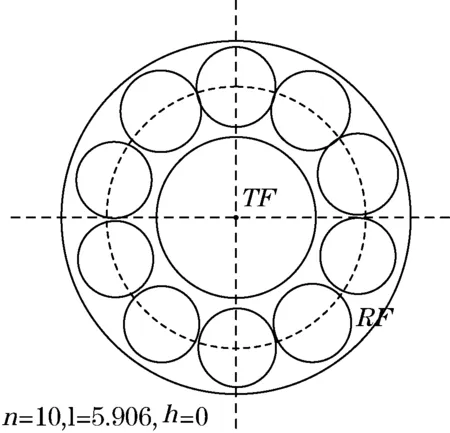
(b)n=10光纤束

依据反射式同轴型光纤束传感器在压力检测中的强度调制函数M，计算出表1中n1=9、n2=10、n3=11、n4=12时各种光纤束结构下的强度调制函数曲线为图4所示。

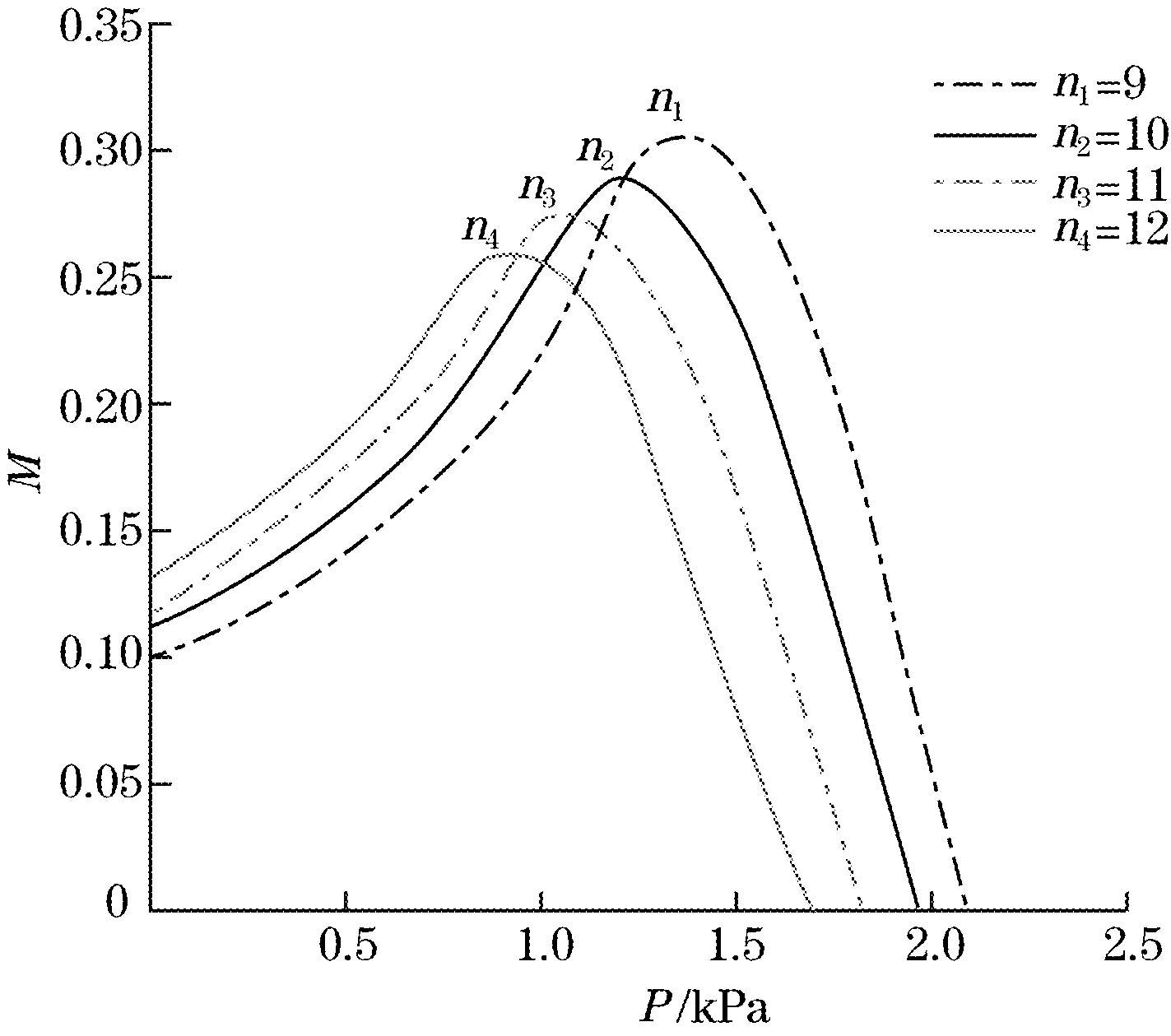
图4　不同光纤束结构P—M曲线

在图4中不难看出当接收光纤数分别为n1=9、n2=10、n3=11、n4=12时，其强度调制P—M曲线的最大值依次减小，即当n1=9时具有最大的强度调制函数峰值，而当n4=12时，是这几种结构中强度调制函数峰值最小的。这与文中前述的光纤束优化设计结果相吻合，证明了当接收光纤与入射光纤的间距越小，排列越紧密时，传感器的输出信号强度越大，灵敏度越高。

3．2对比实验结果

在实验室条件下，更具上述优化设计的结果，自制与购买了3种不同结构的同轴型光纤束进行对比实验。3种光纤束的结构如表2所示，图5为各光纤束的实物图。

表2　3种光纤束结构

图5　光纤束实物图

应用不同结构的光纤束进行反射位移实验，实验中光纤束固定于支架上，接收光纤输出的光信号，通过光电探测器及信号处理模块，转换为电压值输出。首先让反射镜尽量靠近光纤束，再以每次0.2 mm的距离逐渐远离光纤束，记录下每一次位移的输出信号值，如图6所示。

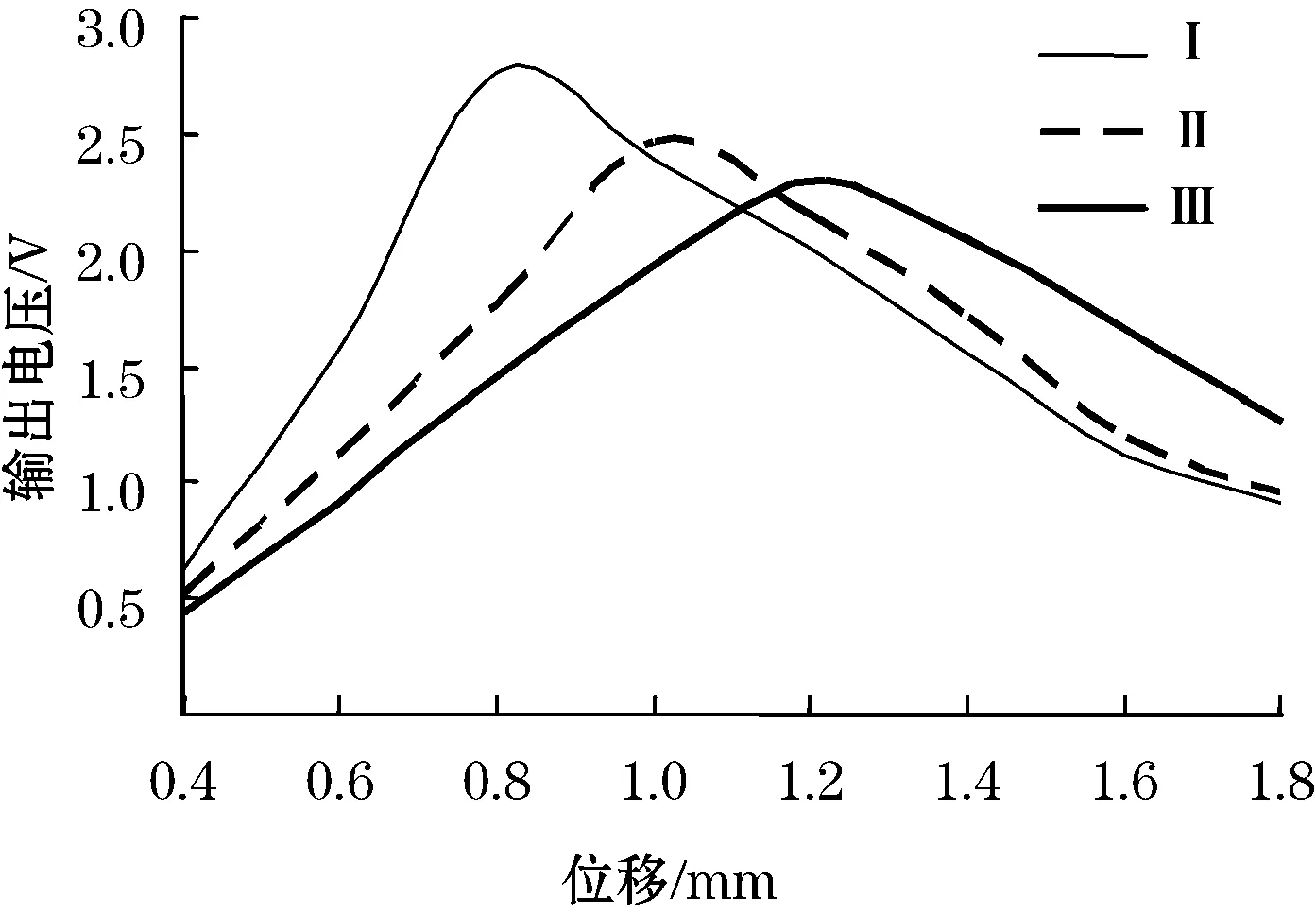
图6　实验数据曲线

从图6中的实验数据得出：光纤束Ⅰ的输出电压峰值最大，为2.8 V左右，其前坡曲线灵敏度约为5.2 V/mm；光纤束Ⅱ的输出电压峰值次之，为2.5 V左右，其前坡曲线灵敏度约为3.3 V/mm；光纤束Ⅲ的输出电压峰值最小，为2.2 V左右，其前坡曲线灵敏度约为2.3 V/mm．不难看出通过优化后的光纤束结构检测灵敏度得到了很大的提高，分别为后两种结构的1.58与2.26倍，这与光纤束结构的优化设计理论结果相吻合。

4　结束语

同轴型光纤束在强度调制型传感器中经常得到使用，但很少有人对其结构的优化进行思考，很多情况都是拿来即用，这就可能出现传感器达不到检测要求、传感器性价比不高、传感器结构不够优化等诸多不足。文中通过优化理论对同轴型光纤束的结构进行设计，从而在提高其传感性能的同时，使得光纤束具有更高的性价比与更优的几何尺寸。以期为这类传感器的设计与使用起到积极的推动作用。

参考文献：

[1]ZAWAWI，ANWAR M．Intensity-modulated fiber optic sensor for health monitoring applications：A comparative review．Sensor Review，?2013，33(1)：57-67．

[2]JASON，NILSSON J．Experimental study of an intensity modulated fiber-optic position sensor with a novel readout system．IEEE Sensors Journal，2008，8(7)：1105-1113．

[3]PUANGMALI，PINYO．Modeling of Light Intensity-Modulated Fiber-Optic Displacement Sensors．Instrumentation and Measurement，2011，60(4)：1408-15．

[4]JASON，NILSSON J．Robustness analysis of an intensity modulated fiber-optic position sensor with an image sensor readout system．Applied Optics，2013，52(16)：3876-3883．

[5]杨华勇，吕海宝．反射面形状对反射式光纤位移传感器理论特性的影响．光学精密工程，2002，10(4)：379-382．

[6]陈幼平，曹汇敏，张冈，等．反射式光纤束位移传感器的建模与仿真．光电子．激光，2005，16(6)：653-658．

[7]张冈，刘东波，陈幼平，等．光纤传感器中光源的驱动与控制．仪表技术与传感器，2006(5)：45-46．

[8]佟成国，杨军，刘志海，等．双弹簧管光纤差压传感器．光子学报，2004，33(10)：1172-1175．

[9]金远强，马惠萍，周岩．基于光强余弦分布的同轴型光纤位移传感器设计．传感器与微系统，2008，27(7)：79-81．

[10]刘丽华，车仁生，李建新，等．三层反射式同轴光纤束位移传感器设计．光学精密工程，2005(13)：25-29．