叠加型组合体尺寸标注的教学分析方法研究

易声耀，尚建忠，徐海军

(国防科学技术大学机电工程与自动化学院，湖南 长沙 410073)

工程图样中的尺寸是图样的重要组成部分，是加工零件、检验零件的重要依据，直接影响零件的制造、加工、测量、检验和使用[1]。因此，国家标准对图样中的尺寸标注的要求是：正确、完整、清晰、合理。组合体尺寸标注是零件工作图尺寸标注的基础，除了性能及工艺性要求外，几乎包括所有零件工作图尺寸标注的内容。组合体标注尺寸的对象是平面图形和几何体。给这些图形注尺寸时，只考虑几何上的完整性。因此，对组合体尺寸标注要求的重点是正确、完整、清晰[2]。

组合体尺寸标注是工程制图和机械制图教学中的难点，许多学生在学完本节内容之后，仍对于尺寸标注思维不明晰，不知道要标注到何种程度才算正确和完整标注，或遗漏，或重复。鉴于此，一些学者试图寻求组合体尺寸标注有效方法和教法[3-10]。典型的如“工程制图课程教学中组合体尺寸标注的三基法”[9]、“用投影特征统计法保证集合体尺寸标注的完整性”[10]等。

组合体尺寸标注之所以成为工程制图教学中的难点，是因为要做到正确、完整、清晰并非易事。尺寸标注是否“正确”，源于对国家标准《机械制图》中关于标注尺寸规定的精通及严格执行；尺寸标注是否“完整”，是要做到既不遗漏标注尺寸，也不会重复标注尺寸，所谓不多不少；尺寸标注是否“清晰”，则源于对国家标准的正确理解，甚至需要创造性的理解。本文就笔者多年来的教学思考和体会，从另外的角度试图探求叠加型组合体尺寸标注的教学分析方法。

1 叠加型组合体尺寸标注的基本分析方法和有关定义

组合体的基本组成方式有叠加和切割两种。而在现实世界中，叠加型组合体更为常见。因此，探求叠加型组合体尺寸标注的有效方法在教学中显得非常重要。

1.1 叠加型组合体尺寸标注的基本分析方法及局限性

对于叠加型组合体，应用形体分析法标注尺寸是基本方法。形体分析法标注尺寸的一般步骤和过程为：①对组合体进行形体分析，假想地将其分解为若干基本几何体；②选取尺寸基准；③逐个标注出各基本几何体的定形尺寸、定位尺寸；④综合分析，标注整体尺寸[11-12]。

对初学者而言，虽然作形体分解并不困难，但标注整体尺寸却并不容易把握。因为应用形体分析法标注尺寸时，并非简单地将每个基本几何体的定形尺寸和定位尺寸进行叠加即可，而是在简单叠加的基础之上，经过综合分析，将一些重复的尺寸剔除掉，才能获得正确和完整的标注。这就使初学者难以把握尺寸标注的数目，遗漏和重复几乎不可避免。

1.2 叠加型组合体的分类及其尺寸的有关定义

为了便于分析，本文先将叠加型组合体分类，并为其尺寸给出一些新的定义。

1.2.1 形体分类

将叠加型组合体按结构分为简单叠加型组合体和关联结构叠加型组合体两大类。

简单叠加型组合体：当构成组合体的若干基本几何体中，任意两相邻的基本几何体在结构上完全独立、互不相关时，称为简单叠加型组合体。如图1所示的支座一。

图1 支座一 (简单叠加型组合体)

关联结构叠加型组合体：若构成组合体的一些相邻的基本几何体在结构上存在某种关联关系时，称之为关联结构叠加型组合体。如图2所示的支座二，其底板之上的另两个部分均依底板结构尺寸而定。

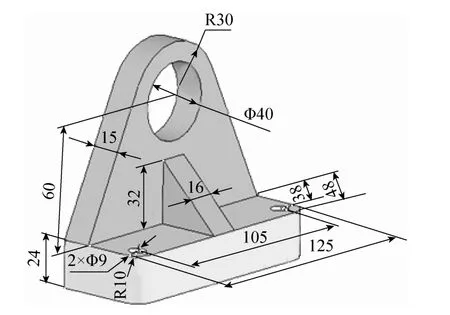
图2 支座二 (关联结构叠加型组合体)

1.2.2 尺寸定义

为了准确把握形体应注出的尺寸类型和数目，本文拓展尺寸定义。即在原有组合体的定形尺寸、定位尺寸、总体尺寸的基础上，新增两种尺寸定义：非约束尺寸和约束尺寸。

非约束尺寸：在对组合体作形体分析时，其形状大小或位置仅由功能决定、而不依赖于相邻基本体形状或位置的基本几何体的定形尺寸或定位尺寸。非约束尺寸又可分为非约束定形尺寸和非约束定位尺寸。

约束尺寸：其形状大小或位置取决于相邻基本尺寸。约束尺寸可分为：约束定形尺寸和约束定位尺寸。

约束定形尺寸一般只出现在关联结构叠加型组合体上，当相邻两基本体的表面连接关系为平齐、相切以及虽不平齐，但结构上对齐的情况时，某一基本几何体的某些定形尺寸随其相邻几何体的结构而定，这一尺寸即为约束定形尺寸。如支座二中的竖板和肋板，假想地分解后，都存在约束定形尺寸。而支座一则不存在约束定形尺寸。在叠加型组合体中，由支架类和箱体类零件抽象而成的复杂组合体多出现此种情况。这类复杂叠加型组合体由较多的基本几何体构成，一般包括工作部分、安装部分、连接部分三大部分。其工作部分和安装部分是形体的主体部分，其形状一般由功能要求决定；连接部分是连接工作部分和安装部分的过渡结构，其形状除了功能要求外，许多情况下随工作部分和安装部分的形状而定。因此，大多会出现平齐、相切或结构上对齐等关联结构的情况。

约束定位尺寸是叠加型组合体常出现的一类定位尺寸。无论是简单叠加型组合体，还是关联结构叠加型组合体，都会有一些约束定位尺寸。图1和图2中的底板厚度24，均作为其上各结构在高度方向的约束定形尺寸。

2 叠加型组合体尺寸标注的分析

2.1 简单叠加型组合体尺寸标注分析

以图1所示的支座一为例，探讨叠加型组合体尺寸标注的分析方法和步骤。

2.1.1 形体分析

用形体分析法假想将其分解为底板、竖板、肋板等3个基本几何体。各基本几何体的定形尺寸标注如图3所示，3个方向的尺寸基准如图4所示。表1列出了各基本几何体的定形尺寸、定位尺寸及其数目。

表1 支座一各基本几何体定形、定位尺寸及其数目

图3 支座一形体分解及各部分的定形尺寸

2.1.2 尺寸分析

由图3和表1可知，该组合体定形、定位尺寸的总和为24个。

实际上，该形体尺寸的完整标注只需要15个尺寸，即如立体图1所示的全部尺寸。这个数目正好是表1中的全部定形尺寸的数目。这说明，该形体只要标全了各基本体的全部定形尺寸，就已经获得了完整的标注。而表中的全部定位尺寸均须剔除不标注。

归纳表中的定位尺寸类型，它们可归为两类：一类是数值为0的定位尺寸；另一类则是约束定位尺寸。

何谓数值为0的定位尺寸？当某基本几何体的轴线、对称面、中性面、底面或某一大端面等其中之一，与组合体整体某一方向的基准重合时，就表示该基本几何体与整体在这一方向的距离为0。如底板长度方向是以其对称面与整体的长度方向基准重合，即长度方向的定位尺寸为0。同理，底板的宽度方向以其最大的后背面与整体的宽度方向基准重合，高度方向以其底面与整体的高度方向基准重合；竖板的长度方向以其中性面与整体的长度方向基准重合，宽度方向以其后背面与整体的宽度方向基准重合；肋板的长度方向也是以其中性面与整体的长度方向基准重合。因此，数值为0的定位尺寸被剔除不标注。

约束定位尺寸不标注，是因为它们是作为主要基本体的定形尺寸已经注出。如竖板、肋板的高度方向的定位尺寸24，肋板的宽度方向的定位尺寸15等，分别是底板的厚度和竖板的厚度，均作为定形尺寸已经注出。

2.1.3 尺寸注出

图1所示支座一的完整标注见图4。图4中仅在形体分析的简单叠加基础上，将竖板原高度尺寸60改为孔Ф40的定位尺寸84，其余均不需作任何改动。即使尺寸60不改，若不考虑工程要求，仅就几何图形的要求而言，完全是可以接受的。

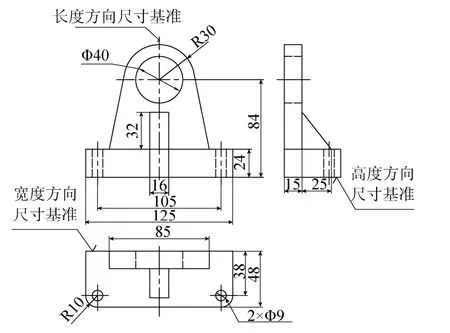
图4 形体分解及各部分的定形尺寸

2.2 关联结构叠加型组合体尺寸标注分析

以图5所示的轴承座为例，来分析关联结构叠加型组合体尺寸标注的方法及其规律。

2.2.1 形体分析

该形体是一个比较典型的关联结构叠加型组合体。用形体分析法假想将其分解为圆筒、支撑板、底板、肋板等4个基本几何体。各基本几何体的定形尺寸标注如图6所示；3个方向的尺寸基准如图7所示。表2列出了各基本几何体的定形尺寸、定位尺寸及其数目。

2.2.2 尺寸分析及标注

由表2可知该组合体定形、定位尺寸的总和为34个。

但该轴承座尺寸的完整标注实际只需要19个尺寸，如图5所注的全部尺寸所示。这说明按照形体分析法标注尺寸时，若只进行简单叠加，则会出现大量的多余或重复标注，这是工程上所不允许的。本例有15个尺寸必须剔去，不仅包括一些定位尺寸，还包括一些定形尺寸。以下试图探求必须剔去的15个尺寸的一般规律。

图5 轴承座立体图

图6 轴承座的形体分解及各部分的定形尺寸

表2 轴承座的各基本几何体定形、定位尺寸及其数目

(1) 剔除数值为0的定位尺寸：照2.1的道理和方法，剔除表2中7个数值为0的定位尺寸不标注。剩下的尺寸个数为34-7=27个。也即还有8个尺寸需要剔除掉。

图7 轴承座3个方向尺寸基准和尺寸标注

(2) 进行尺寸分析：将表2中的所有定形尺寸和数值不为0的定位尺寸按前述尺寸定义重新分类，如表3所示。

非约束尺寸：在轴承座中，底板和圆筒的所有定形尺寸、支撑板厚度尺寸12、肋板的厚度尺寸14以及其上另3个尺寸6、16和18等，其大小仅由功能决定、而不依赖于相邻基本体结构形状，均为非约束定形尺寸。而圆筒的高度方向定位尺寸62和宽度方向定位尺寸6，其位置仅由功能决定、而不依赖于相邻基本体的位置关系，则是数值不为0的非约束定位尺寸。

表3 轴承座各基本几何体的数值不为0的非约束尺寸和约束尺寸及其数目

对于数值为0的定位尺寸，上述已经阐明无需标注。不过，就其本质而言，数值为0的定位尺寸都是非约束的。因为当基本体的某一方向定位尺寸数值为0时，该定位尺寸即是基本体本身相对于基准之间的距离，而非与相邻基本体之间的关系。因为无需标注，因此也就不必考虑其约束或非约束的性质了。

约束尺寸：支撑板底端的长度取决于底板的长度尺寸76，其高度及上部形状取决于圆筒的定位尺寸62与定形尺寸Ф44，其孔槽即为圆筒的定形尺寸Ф44。同理，肋板的高度和圆弧槽也取决于圆筒的62与Ф44。因此，支撑板、肋板的这些尺寸均为约束定形尺寸。而支撑板、肋板的高度方向定位尺寸18取决于底板的高度(厚度)，肋板的宽度方向定位取决于支撑板的厚度12，因此，支撑板、肋板的这些定位尺寸均为约束定位尺寸。

自表3可以看出，非约束定形尺寸与数值不为0的非约束定位尺寸之和为17+2=19，这些都是需要标注的尺寸。而约束定形尺寸与约束定位尺寸之和为5+3=8，这些都是需要剔除不标注的尺寸。其中，支撑板的定形尺寸Ф44、44、76、肋板的定形尺寸Ф44、44等5个尺寸，均为约束定形尺寸；而支撑板高度方向定位尺寸18、肋板高度方向定位尺寸18、宽度方向定位尺寸12等3个尺寸，均为约束定位尺寸。

经过以上的分析，最后注出轴承座的全部尺寸如图7所示。图上仅留下确实应该标注的19个尺寸，不多不少，获得轴承座尺寸的完整标注。

2.3 叠加型组合体尺寸标注的原则

综合以上对两类叠加型组合体尺寸标注的分析，本文得出应用形体分析法标注叠加型组合体尺寸时，应遵循的3条原则，归纳如下：

(1) 所有数值为0的定位尺寸均不标注；

(2) 所有约束尺寸均不标注；

(3) 所有非约束定形尺寸和数值不为0的非约束定位尺寸均应标注。

掌握以上尺寸标注原则，可正确、完整地标注叠加型组合体尺寸。对图2所示的支座二进行尺寸标注，应用此3条原则可知：形体分解后，得到15个定形尺寸(底板125、105、48、38、24、2×Ф9、R10；竖板Ф40、R30、125、15、60；肋板16、32、33)，9个定位尺寸(各数值均同支座一，见表1)，总尺寸数为24个。其中，15个定形尺寸中有2个约束定形尺寸(竖板尺寸125、肋板尺寸33)；9个定位尺寸中，6个数值为0，其余3个均为约束定位尺寸。因此，标注时应将9个定位尺寸和2个约束定形尺寸共11个尺寸剔除，得到必须注出的尺寸个数为24-11=13个，即是完整标注图上的尺寸数目。同时得知那些尺寸必须注出。

3 结束语

组合体尺寸标注作为工程制图或机械制图课程教学中重点内容，在课程内容体系中占有重要位置。而作为教学中的难点，是因为目前的标注方法还不易于为学生所接受与掌握。本文对叠加型组合体的尺寸标注教学分析方法作了一定程度的研究，主要内容有以下3点：

(1) 将叠加型组合体按结构分为简单叠加型组合体和关联结构叠加型组合体两大类，继而按类分析了其尺寸标注的步骤。

(2) 通过定义约束尺寸和非约束尺寸，探索了一种能容易接受和掌握的叠加型组合体尺寸标注的方法和规律，用此法能较好地标注叠加型组合体的尺寸。

(3) 经过综合总结，得出了叠加型组合体尺寸标注的3条原则。

本文最后得出的叠加型组合体尺寸标注的3条原则，应该为教学分析提供方便。

[1]秦小琼.“组合体尺寸标注”的图例讲解[J].甘肃广播电视大学学报, 2000, 103: 69-71.

[2]苏秀英.尺寸标注方法的探讨[J].天津轻工业学院学报, 1995, 2: 82-85.

[3]刘桂书.组合体尺寸标注教学浅析[J].长江水利教育,1996, 3: 36-37.

[4]陆国栋, 晏 群, 曹 敏.关于尺寸标注的教学方法改革探讨[J].浙江工业大学学报, 2000, 28(S1): 177-180.

[5]贺金华, 刘志儒.尺寸标注完整性探讨[J].机械研究与应用, 2004, 17(2): 21-22.

[6]殷小清.组合体尺寸标注规律探讨[J].机械工业标准化与质量, 2007, (3): 26-30.

[7]许淑慧.尺寸标注常见问题及对策探析[J].机械工程与自动化, 2008, (3): 192-193,195.

[8]张爱莲, 陈书剑.组合体尺寸标注中几个问题的探讨[J].广西轻工业, 2009, 25(11): 41-42.

[9]胡 东, 唐川林, 曾 莹, 王菊槐.工程制图课程教学中组合体尺寸标注的三基法[J].湖南工业大学学报, 2011, 25(3): 97-100.

[10]李唯东, 杨胜强.用投影特征统计法保证集合体尺寸标注的完整性[J].机械管理开发, 2007, (4): 56-57.

[11]杨惠英, 王玉坤.机械制图[M].北京: 清华大学出版社, 2002: 107-110.

[12]张 彤, 樊红丽, 焦永和.机械制图[M].2版.北京:北京理工大学出版社, 2006: 193-197.