后向投影成像算法的GPU优化方法研究∗

班阳阳,张劲东,陈家瑞,邱晓燕

(南京航空航天大学电子信息工程学院,江苏南京210016)

0 引言

合成孔径雷达(SAR)是一种全天时、全天候的微波成像雷达,能够对飞机、舰船和导弹实现超视距检测[1],高分辨率的特点使它在军用和民用领域有着不可替代的作用。随着合成孔径雷达成像技术的发展,各种高分辨率成像算法应运而生。然而高分辨率带来巨大的计算量成为某些成像算法实际应用的瓶颈,其中最为典型的就是后向投影(Back Projection,BP)算法。BP成像算法是一种时域成像算法,其成像过程就是计算各方位时刻雷达平台位置与目标点的双程延时,再将不同方位时刻对应的回波信号进行相干累加,最后得出目标函数的过程。BP算法在原理上不存在任何理论近似,因此成像效果更好;但是逐点成像计算的过程,使得该算法运算量巨大[2]。

近年来,GPU技术的迅速发展为大规模数据的计算与分析提供了一种新的技术手段。与CPU相比,GPU明显具有成本低、性能高的特点。目前Fermi与Kepler架构的出现,使得GPU通用计算的性能有了飞速的提升[3]。在此基础上,各种复杂的SAR成像处理算法在GPU上得到加速实现。文献[4]对高分辨率星载SAR成像中ECSA(Extended Chirp Scaling)算法提出了一种加速方案,并在NVIDIA Tesla C2075上面实现了6～8倍的有效加速;中科院电子所针对距离多普勒(Range Doppler,RD)算法、CS(Chirp Scaling)算法及ω-k算法提出了不同的加速方案,并在NVIDIA K20C上面实现了每秒约36 MB采样点的实时处理[5]。文献[6]对复杂场景的SAR成像进行实时仿真,把计算机的相关技术应用到SAR图像仿真中去,充分利用GPU的可编程图形管线,实现了三维复杂场景的建立和实时阴影的生成。

本文以后向投影成像作为算法基础,研究了GPU设计中的多流异步执行技术、数据传输模式和计算速度与精度,提出了一种在聚束模式下针对BP成像的GPU优化方案。该方案充分利用后向投影算法内在的并行性,最大程度地利用GPU设备的计算资源,使得成像速度与GPU非优化方案的实现相比有了近一倍的提升。

1 后向投影算法的并行化分析

BP算法主要包括距离向压缩和反投影两个部分。它假设发射波是冲激球面,通过回波在时域的相干叠加实现高分辨率成像。慢时间域相干叠加的成像结果可表示为

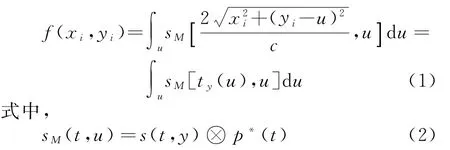
因此,后向投影算法的过程是一个点对点的图像重建过程,在反投影过程中需要数量巨大的插值操作,导致运算量巨大。以Na×Nr的回波数据为例(其中Na和Nr分别为方位向和距离向点数),成像网格方位向和距离向点数分别为Nia和Nir,假设Na、Nia和Nir都为N,那么后向投影中插值的计算量就为O(N3)。除了插值运算本身之外,斜距计算和相位补偿等操作在CPU计算中也是非常耗时的,这些因素制约了该算法在CPU平台上的应用和发展。

GPU最大的特点是采用了SIMT(Single Instruction Multiple Threads)组织模式管理硬件中同时存在的线程,实现对所有数据的并行处理[7]。同时,GPU在线程的组织管理中采用了单线程(Thread)、线程块(Block)以及线程格(Grid)的方式,将线程与GPU硬件中的流多处理器(Streaming Multiprocessor,SM)和流处理器(Streaming Processor,SP)进行了映射。

对后向投影算法的分析可知,不同网格点的反向投影操作过程完全相同并相互独立,这使得后向投影算法在GPU上并行实现成为可能。我们可以通过为每个成像网格点分配一个独立工作的线程,每个线程都单独执行斜距计算、插值、相位补偿等操作,最终完成对每个像素点的反投影计算。后向投影算法的GPU并行计算分配示意图如图1所示,对于Nia×Nir的成像网格,一共分配Nia×Nir个并行线程,其相应的并行度为Nia×Nir。

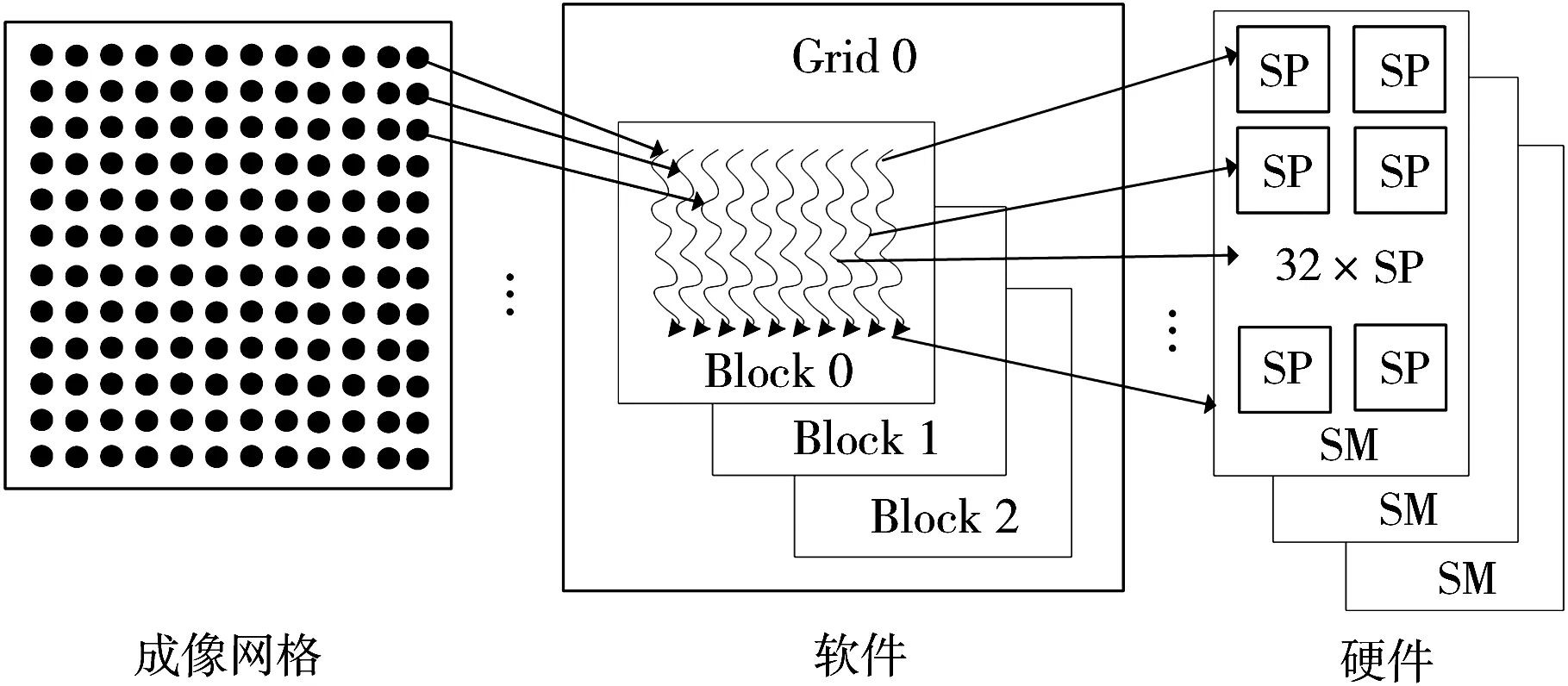
图1 后向投影算法的GPU并行计算分配图

值得注意的是,在GPU中所谓的“并行”执行并不严谨,实际情况下是“并发”执行的[8]。由于硬件资源的限制,在理想条件下,并行运算所能获得的加速比等同于并行度,但由于并行处理所涉及的GPU资源分配及调度等原因,在实际情况下加速比要低于并行度。尽管如此,并行度为Nia×Nir的反投影操作经过并行处理后依然能获得相当高的加速比。

2 后向投影算法的GPU设计

2.1 算法设计流程

图2是后向投影算法在CPU+GPU上实现的流程图。后向投影算法实质上是在CPU+GPU异构平台上完成的,GPU负责完成数据级并行的操作,包括距离向脉冲压缩以及反投影,CPU则主要负责简单的串行操作。

2.2 脉冲压缩

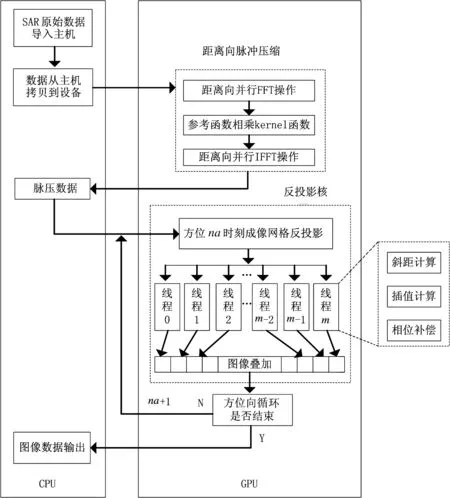
图2 利用CUDA实现基于CPU+GPU的后向投影成像算法流程图

后向投影算法的距离向压缩和传统SAR成像算法一样,包含3个部分：回波数据距离向FFT、参考函数和FFT后的数据相乘、相乘后数据进行IFFT。CUDA有自带的FFT库,即CUFFT库,它是一个基于CUDA编程环境下的FFT库,支持多个分段数据批量进行一维FFT以及IFFT运算,该库对FFT以及IFFT操作能够达到很高的运算性能[9-10],为距离向脉压提供了极大的方便。

如图2所示,首先将Na×Nr的SAR回波数据从CPU拷贝到GPU,接着对Na×Nr的数据进行距离向脉冲压缩处理,主要包括对回波数据分段批量进行一维FFT、在编写的核函数内进行参考函数相乘以及将相乘结果分段批量进行一维IFFT等操作,最后将脉冲压缩后的数据从GPU拷贝到CPU。其具体实现步骤如下：

(1)在主机端申请Na×Nr大小的内存来存储距离压缩后的数据,同时在设备端也申请相同大小的显存并完成数据从主机端到设备端的拷贝。

(2)使用CUFFT库中的cufft Handle制定FFT计划plan,并使用cufft Plan1d制定FFT方案,即cufftPlan1d(&plan,Nr,CUFFT_C2C,Na),对Na×Nr长度的数据分段批量作FFT;再调用cufftExecC2C函数分段批量完成回波数据的一维FFT。

(3)编写核函数完成FFT后的数据与参考函数的点乘,并将结果存入已经分配好的显存内。

(4)与步骤(2)类似,再次调用cufft ExecC2C函数对步骤(3)中显存内的数据并行批量完成一维IFFT,完成距离向压缩。

(5)考虑到GPU显存容量,将脉冲压缩后的数据拷贝到主机端,并释放掉在显存上申请的空间。

2.3 反投影

如图2所示,反投影操作沿着方位向依次进行,方位时刻na(0≤na≤Na-1)的反投影操作包括na时刻脉压数据以及必要参数从CPU拷贝到GPU、反投影核函数执行。在同一方位时刻,对于Nia×Nir大小的成像网格,为核函数分配Nia×Nir个并行线程,核函数中的每一个线程独立完成网格中一个点的反投影操作,包括距离计算、插值计算、相位补偿,不同方位时刻的反投影结果相叠加并存储在设备端,方位向操作完成后将最终的图像数据拷贝到主机。

反投影操作主要包括斜距计算、插值和相位补偿。对于Nia×Nir大小的成像网格,首先在设备上为成像网格分配一个Nia×Nir的存储空间H0,并初始化为0,以存储GPU上反投影的叠加结果,同时在主机上也分配一个同样大小的内存空间Hl以存储从设备上拷贝回来的反投影数据。计算任意方位时刻雷达平台与网格点之间的斜距R(t)求得双程延时td,由BP算法原理可知,利用此延时构造多普勒相位补偿因子ej2πfctd来进行相位补偿。在SAR成像处理过程中,距离压缩后的数据都为离散信号,上面求得的双程延时很难刚好匹配于采样点,所以需要对距离压缩后的回波数据进行插值重采样,以实现精确的相位补偿。每个方位时刻的反投影结果均与H0叠加并更新H0中的数据,一直到方位向操作全部结束,H0图像数据更新完成,并将H0数据拷贝回主机上事先分配好的内存Hl里。

插值重采样一般采用线性插值、最邻近点插值以及8点sinc插值等。无论哪一种插值方式,都要通过斜距求出待插点位置,然后根据位置进行插值。由2.1节可知,在插值核内为每个网格点的插值分配一个独立的线程,线性插值和最邻近插值只需要根据待插点位置便可一次性求出待插点的值,而8点sinc插值则需要在单个线程内完成8次循环才能完成插值操作。目前主流的CPU主频超过1 GHz、2 GHz,甚至3 GHz,而主流GPU的主频在500～600 MHz,性能好的在1 GHz左右。从主频来看,GPU执行每个数值计算的速度并没有CPU快,所以在GPU上编程要尽量避免单线程循环操作。基于以上分析,在GPU上实现8点sinc插值要比线性插值和最邻近插值耗时长久。

3 GPU算法优化

3.1 基于多流异步执行技术的脉冲压缩优化

如图2所示,距离向脉冲压缩过程是先将SAR原始数据从CPU拷贝到GPU,完成距离向脉冲压缩之后再将数据由GPU拷贝到CPU。为了隐藏数据在主机内存与设备显存之间的交互传输,充分利用GPU设备的计算资源,本文将利用CUDA多流异步执行技术[11]来优化此过程。首先创建4个流,并将SAR数据按方位向分块并分别交由流0、流1、流2和流3处理,每个流单独完成本块数据的脉冲压缩操作,包括“CPU→GPU数据拷贝、脉压处理、GPU→CPU数据拷贝”三项任务。流之间同类处理任务不能并行执行,不同种类的处理任务可以并行执行。在整个任务处理过程中,除了首位部分时间4个流未完全并行外,中间处理过程都处于并行执行状态。由于GPU上的计算单元一直处于工作状态,从而有效隐藏了数据在主机和设备之间的传输时间。具体执行过程如图3所示。

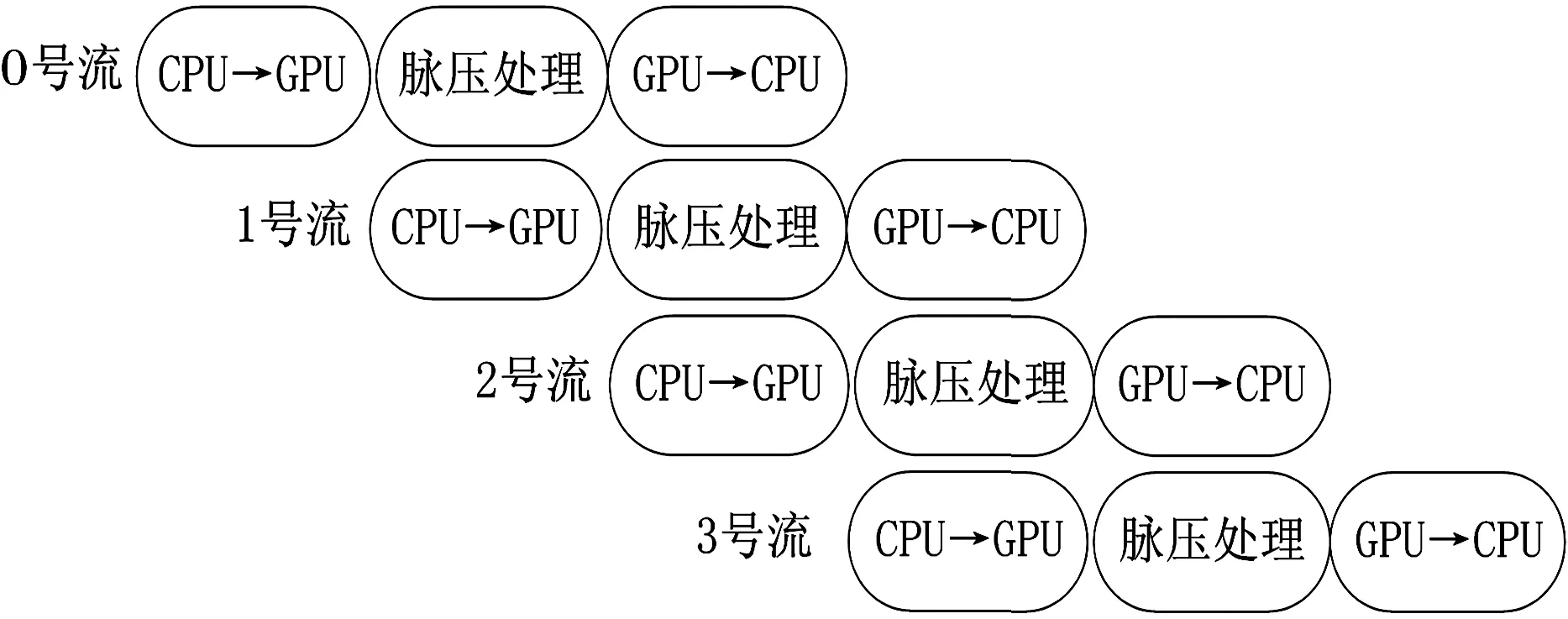
图3 多流异步执行流程图

3.2 反投影计算结构优化

如图2所示,在反投影过程中习惯将脉压数据沿方位向依次拷贝到GPU,即每个方位时刻的反投影过程都包括CPU→GPU数据拷贝以及核函数执行两个部分。反投影计算过程优化之前的流程图如图4所示。

图4 优化之前执行流程图

在CUDA架构中,只有使计算单元一直处于工作状态才能充分利用GPU资源,而由传统设计方案来看,在数据拷贝到GPU之前,GPU计算单元会一直处于等待状态,使得GPU资源没有充分得到利用。为了解决以上问题,在反投影操作前将待用的数据拷贝到GPU内存H2,然后在核函数中根据na计算出的偏移量在H2中选择当前方位时刻需要的数据进行反投影操作。这样在沿方位向进行反投影操作的时候,不同方位时刻的核函数就会连续执行,充分利用了GPU的计算资源。反投影计算过程优化之前的流程图如图5所示。

图5 优化之后执行流程图

3.3 计算精度与速度优化

本文中的GPU实验平台为NVIDIA Tesla C2075,共有448个CUDA cores,6 GB显存以及1.15 GHz的时钟频率。Tesla C2075是NVIDIA公司为高性能计算量身打造,通过加入一颗Tesla协处理器,使其拥有高速的浮点计算能力,更适合用于以浮点运算为主的计算任务,并且可以执行符合IEEE-754标准的硬件双精度计算。

成像质量和成像速度是本次实验的两个主要指标,由于后向投影成像算法对精度要求相对较高,所以在满足精度要求的情况下,最大限度的提高计算速度是本实验追求的主要目标。双精度虽然能取得很好的成像效果,但其实现效率却不太理想。反投影操作中要进行相位补偿,需要计算sin和cos值,sinf(x)、cosf(x)及相应的双精度指令开销非常昂贵,尤其是x绝对值较大时更是如此,而用CUDA自带的__sinf(x)、__cosf(x)函数吞吐量却能达到每个时钟周期一个操作;考虑到sin和cos函数对小数位的精度要求不高,并且当使用单精度时可以用__sinf和__cosf函数进行加速,所以为了提高计算效率,本实验将使用混合精度来计算,即相位补偿计算用单精度进行替换。本实验中的波长λ为0.03 m,雷达与网格点之间的斜距R为10 000 m左右,相位补偿因子4πR/λ的量级为107,此情况下数值较大不能直接使用__sinf和__cosf函数进行加速。基于余弦的周期性,先对相位补偿因子进行如下处理：

处理完之后数量级减小,则可以直接用-sinf和-cosf函数进行加速。

4 CPU与GPU计算结果测试

本文中所用实测数据来自某型机载雷达所录取,该雷达工作在X波段,以聚束模式采集数据;点目标仿真数据参数和实测数据参数相同,均为聚束模式数据。SAR仿真数据方位向大小Na为4 096,距离向大小Nr为32768,成像网格大小Nia×Nir为512×512,网格间隔大小为0.1 m×0.1 m。表1是本文用到的SAR实验数据的相关参数。

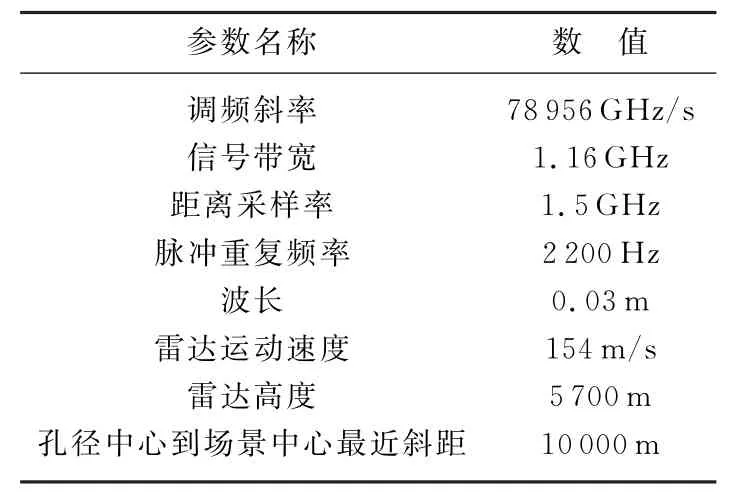
表1 SAR成像参数

图6为线性插值下算法优化前后中心点目标脉冲压缩后的等高线图。

线性插值下脉冲压缩优化前后耗时对比图如图7所示。

在多次计算求出平均耗时时间(不包括内存/显存的分配和释放时间),(a)情况下脉冲压缩耗时507.880 1 ms,(b)情况下耗时267.892 1 ms,优化后的计算效率比优化前提升了将近一倍。

反投影优化前后耗时对比图如图8所示。

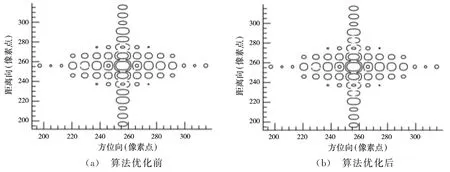
图6 线性插值点目标仿真图

图7 脉冲压缩耗时图

图8 反投影耗时图

在多次计算求出平均耗时时间,(a)情况下脉冲压缩耗时1 936.326 8 ms,(b)情况下耗时1 100.356 1 ms,优化后的计算效率比优化前提升了将近一倍。

表2是基于CPU/GPU不同插值方法下成像速度的比较。

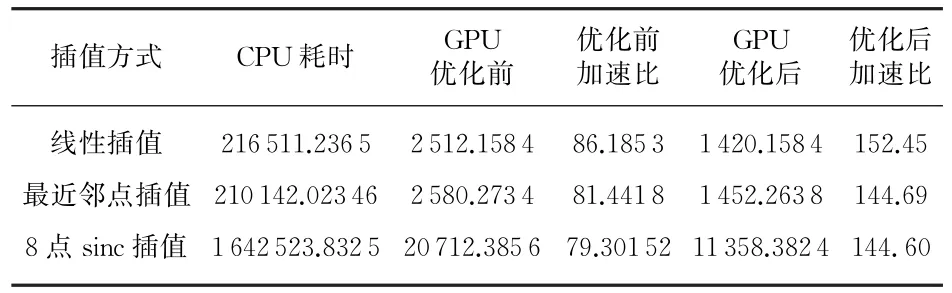
表2 基于CPU/GPU下不同插值方法成像时间对比(混合精度) ms

综上结果分析可知,BP成像算法在GPU和CPU成像质量相当,并且该算法在GPU上得到了150倍左右的加速,GPU优化后的算法比优化前速度提升了约一倍。另外由成像时间可知,线性插值速度最快,其次是最近邻点插值,8点sinc插值速度最慢,这也验证了之前的理论分析。

使用以上方案对实测数据进行成像处理,下面给出线性插值下实测数据分别在CPU和GPU上的成像结果,成像网格大小为512×512,网格间隔大小为0.8 m×0.8 m,如图9所示。

本文通过图像熵和图像对比度准则来判定图像质量。图像熵的公式如下：

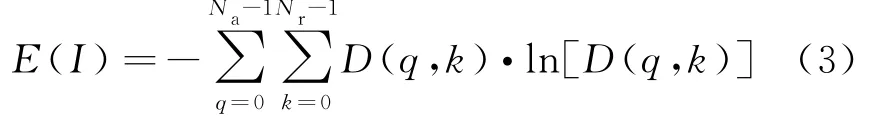
式中,0≤q≤Na-1,q为方位向索引,Na为方位向脉冲个数;0≤k≤Nr-1,k为距离单元索引,Nr为距离单元个数;D(q,k)为图像的散射强度密度,且

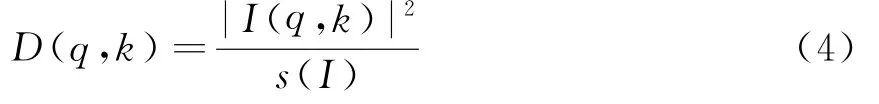
图9 实测数据成像图

图像对比度的公式如下：

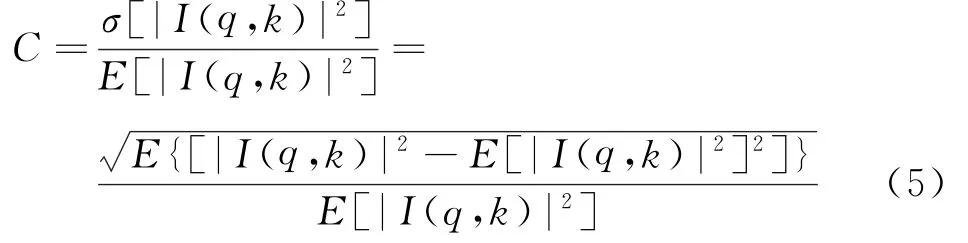
式中,σ(·)表示方差,E(·)表示均值,|I(q,k)|2表示图像各点的像素强度。对于给定的SAR图像,E[|I(q,k)|2]表示信号能量,是一常数。

由表3可知,GPU成像质量和CPU成像质量相当,具有很好的成像效果。

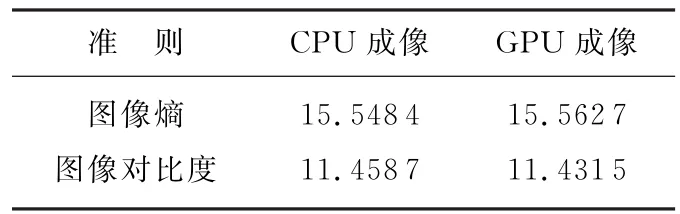
表3 CPU与GPU成像质量比较

5 结束语

本文主要研究了GPU设计中的多流异步执行技术、数据传输模式和计算速度与精度,提出了一种针对BP成像的GPU优化方案。该方案利用全新的GPU通用计算开发理念和编程模型,在低成本硬件的条件下,最大程度地加速了该算法的实现,与GPU非优化方案相比有了近一倍的速度提升。

CUDA环境下基于GPU的成像算法实现,解决了单核CPU甚至是多核CPU计算能力不足的难题,最大限度地加速了复杂算法的实现。将算法的并行性最大限度地与GPU的编程框架相结合,充分利用GPU强大的计算能力和低廉的计算成本,开发出新型的SAR成像处理系统,以应对SAR成像领域目前面临的新挑战。

[1]陈辉,雷霆,闫达亮.天波超视距雷达作战效能综合评估研究[J].雷达科学与技术,2014,12(2)：127-132.CHEN Hui,LEI Ting,YAN Da-liang.Comprehensive Evaluation of Combat Efficiency of Sky Wave OTHR[J].Radar Science and Technology,2014,12(2)：127-132.(in Chinese)

[2]聂鑫.SAR超高分辨率成像算法研究[D].南京：南京航空航天大学,2010：14-17.

[3]LAI J,SEZNEC A.Performance Upper Bound Analysis and Optimization of SGEMM on Fermi and Kepler GPUs[C]∥2013 IEEE/ACM International Symposium on Code Generation and Optimization(CGO),[S.l.]：IEEE,2013：1-10.

[4]侯明辉.基于GPU的高分辨率星载SAR成像处理研究[J].电子科技,2013,26(10)：29-32,35.

[5]孟大地,胡玉新,石涛,等.基于NVIDIA GPU的机载SAR实时成像处理算法CUDA设计与实现[J].雷达学报,2013,2(4)：481-491.

[6]卢媛.基于GPU的复杂场景实时SAR仿真[D].上海：上海交通大学,2010：27-54.

[7]张舒,褚艳利.GPU高性能运算-CUDA[M].北京：中国水利水电出版社,2009：20-24.

[8]VOLKOV V,KAZIAN B.Fitting FFT onto the G80 Architecture[D].Berkeley：University of California,2008：40.

[9]GOVINDARAJU N K,LLOYD B,DOTSENKO Y,et al.High Performance Discrete Fourier Transforms on Graphics Processors[C]∥Proceedings of the 2008 ACM/IEEE Conference on Supercomputing,[S.l.]：IEEE Press,2008：1-12.

[10]SANDERS J,KANDROT E,聂雪军.GPU高性能编程CUDA实战[M].北京：机械工业出版社,2011：40-45.