基于滑模算法的航空稳定平台控制∗

常九健,倪田荣,梅 亮

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

机载稳定平台可以搭载航空相机、合成孔径雷达等设备,广泛应用于军事、公安、消防、环境监控等领域[1]。由于机载稳定平台系统装载在飞机上,载机的姿态变化、振动和飞行中的风阻力矩会造成稳定平台伺服系统的速度波动,从而影响视轴指向不稳定,最终对观测设备的清晰成像产生显著影响[2]。因此在航空复杂气候环境条件下如何使稳定平台系统提高自身的抗干扰能力就显得非常重要。

传统的PI控制方式,鲁棒性较差,容易受到变化负载力矩的干扰[3]。滑动模态控制(SMC)具有鲁棒性、快速性和实现简单等优点。通过迫使系统结构在动态过程中作有目的的改变,使系统运动达到并保持在预定的滑模线上滑动,从而使系统对外部扰动、不确定因素、参数变化以及数学描述的不准确性具有不变性。SMC算法简单、易于工程实现,为复杂控制问题提供了一种很好的解决途径[4]。

本文的航空稳定平台采用永磁同步电机直接驱动的方式,首先建立永磁同步电机直接驱动的数学模型,然后对采用PI控制和滑模控制的试验系统进行仿真分析和实验测试。

1 PMSM的数学模型

为了简化分析,在建立永磁同步电动机数学模型时,作如下处理：(1)假设转子永磁磁场在气隙空间分布为正弦波,定子电枢绕组中的感应电动势也为正弦波;(2)忽略定子铁芯饱和,认为磁路为线性,电感参数不变;(3)不计铁芯涡流与磁滞损耗;(4)转子上无阻尼绕组[5-6]。采用id=0的PMSM转子磁场定向控制,电压方程如下：

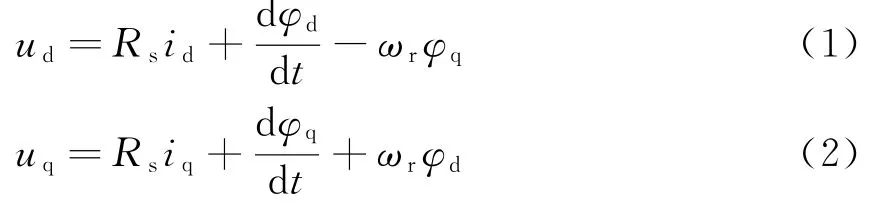
当采用矢量控制方式时,电机的力矩方程可以表示为

式中,Te为电机产生的电磁力,p为永磁体极对数,φf为永磁体产生的磁链,iq为电流环的交轴电流,J为伺服系统的转动惯量,ω为系统转动角速度,B为系统粘滞摩擦系数,TL为负载力矩。交轴电流iq为控制量,定义状态变量为角速度误差,即

式中,ωr为系统参考角速度。

系统的状态方程为

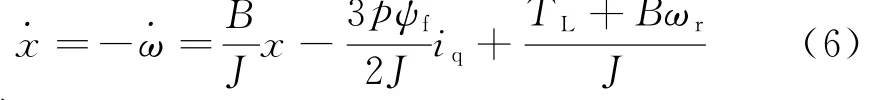
定义：

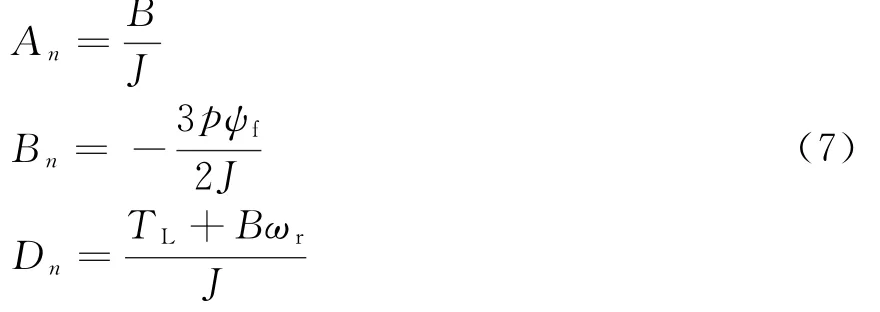
则系统状态方程可以表示为

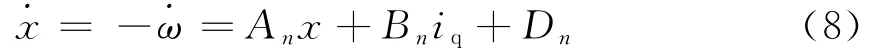
稳定平台伺服系统在运动过程中会受到外界风阻、振动等干扰力矩的影响。这些干扰力矩可以统一看作是负载力矩的变化,此处主要考虑这些干扰力矩对伺服特性的影响,则状态方程可以表述为

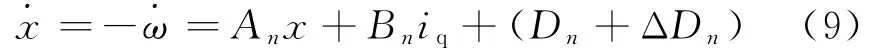
式中,ΔD n为干扰力矩。

为了使系统始终运行在滑模面上,本文滑模面设计采用积分滑模面,控制律采用函数切换控制方式。

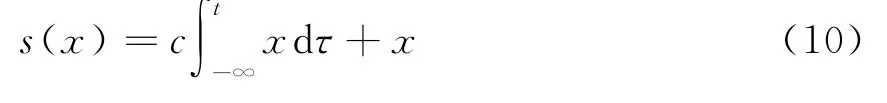
当系统运行在滑模面上时

将式(9)、(10)代入式(11),并令干扰力矩ΔD n=0,可以得到控制变量即交轴电流的等效控制部分：

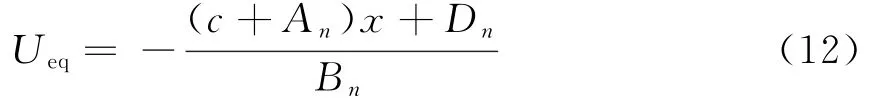
Usw为滑模切换控制部分,通过高频的切换控制,使系统状态趋向滑模面,并保证系统状态沿着滑模面滑向稳定点,实现对不确定性和外加干扰的鲁棒控制,使系统具有很强的鲁棒性。控制律设计为函数切换控制,滑模切换控制部分设计为

最终的滑模控制器设计为

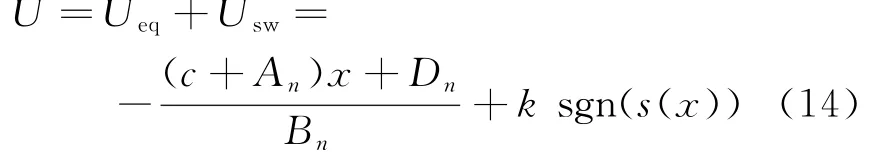
下面进行滑动模态的存在和稳定性条件验证。

由式(9)、(10)和(12)可得

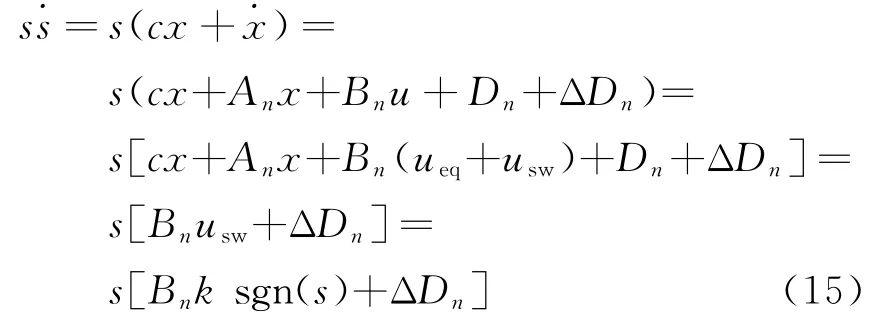
此处

则式(15)化简为

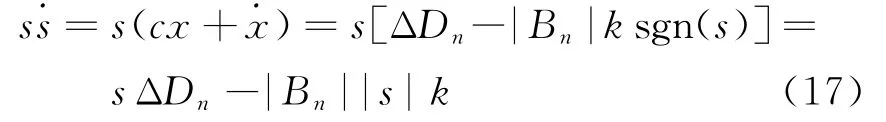
为了使系统存在滑动模态则

则系数k应该满足

为了使系统在任何干扰力矩下具有鲁棒性,即系统稳定性的条件应为

2 稳定平台伺服系统速度环滑模控制仿真

本文在MATLAB中对滑模控制进行建模仿真,电机的相关参数如表1所示。

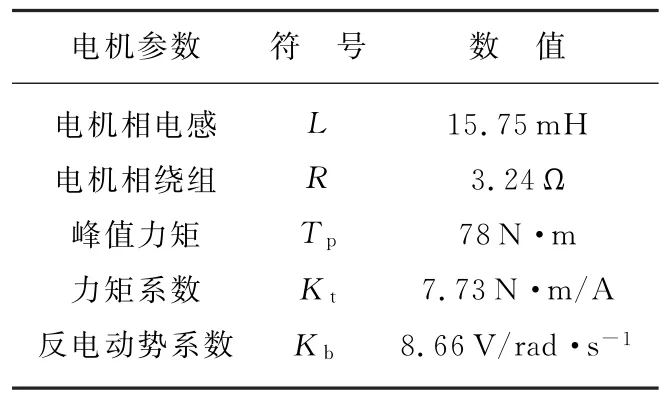
表1 永磁同步电机参数

模型中负载摩擦力矩为0.5 N·m,扰动力矩频率为20 Hz,幅值为0.1 N·m的正弦函数。滑模控制的系统模型和滑模控制子模块分别如图1和图2所示。

在额定速度为0.1 rad/s的情况下,得到的滑模控制速度响应曲线和普通PI控制的速度响应曲线如图3所示。

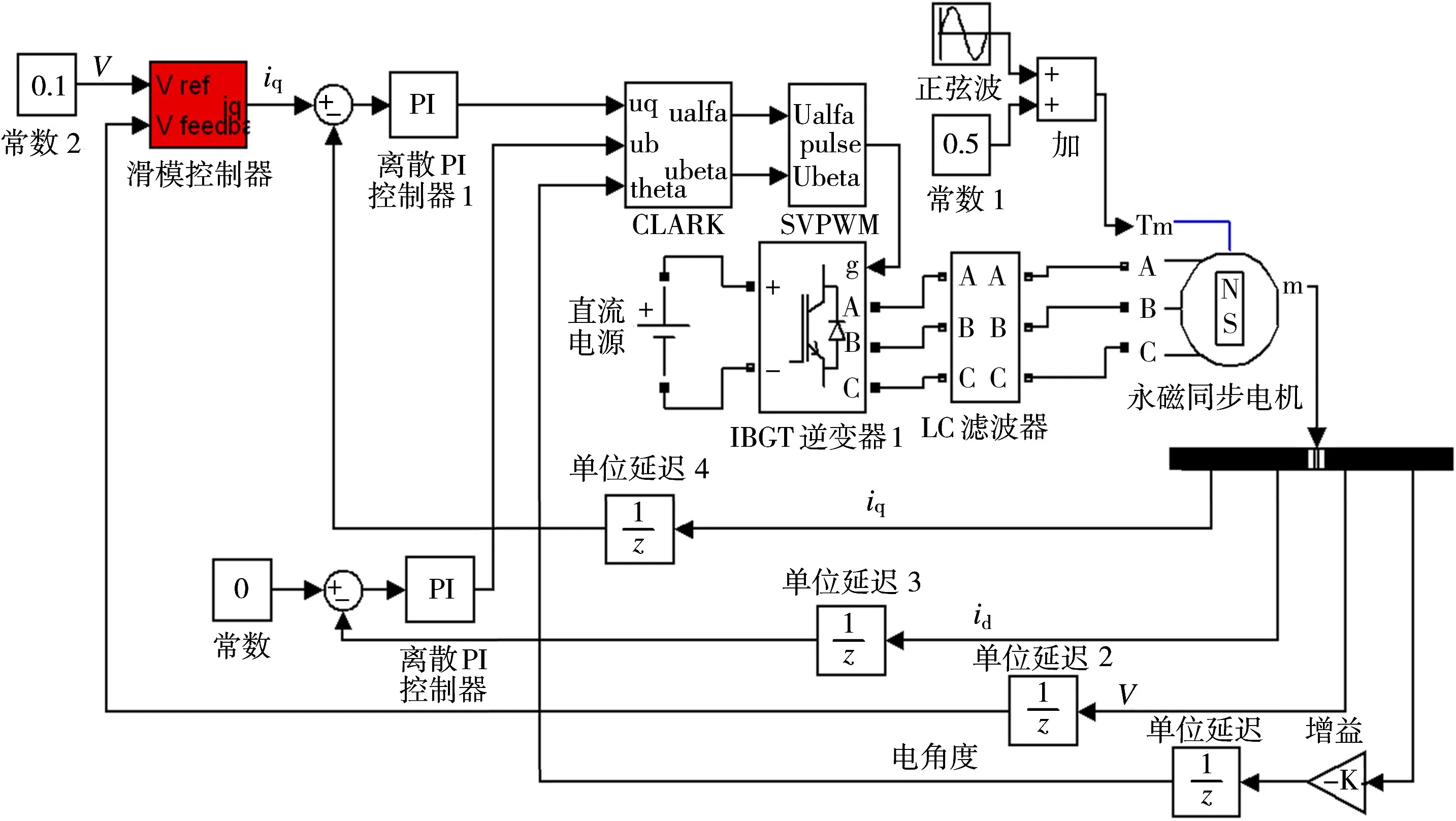
图1 稳定平台系统速度滑模控制

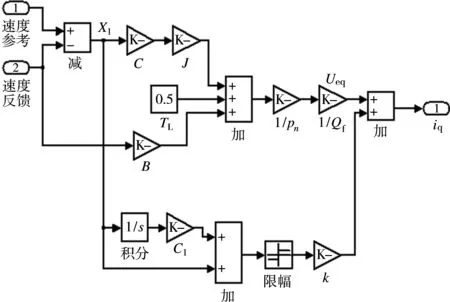
图2 滑模控制子模块

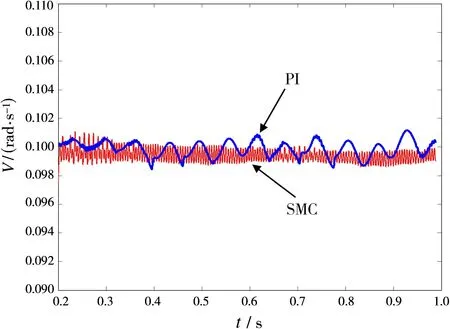
图3 滑模控制速度响应曲线

从仿真结果中可以发现,由于干扰力矩的影响,普通的PI控制容易受到干扰力矩的影响,速度存在明显的周期波动。而滑模控制有较强的鲁棒性,对干扰力矩有较强的鲁棒性,能较好地跟踪给定的速度。

3 稳定平台伺服系统速度环滑模控制实验测试

为了测试伺服系统参数变化对跟踪精度的影响,本文在电机正常运行的情况下突加负载,通过对比速度波动和跟踪精度的变化来验证滑模控制的鲁棒性。

电机初始状态下转台空载运行,t=20 s时刻突加60 kg的惯性负载。控制系统采用普通PI控制和滑模控制得到的速度波动分别如图4和图5所示,得到的跟踪精度如图6和图7所示。

4 结束语

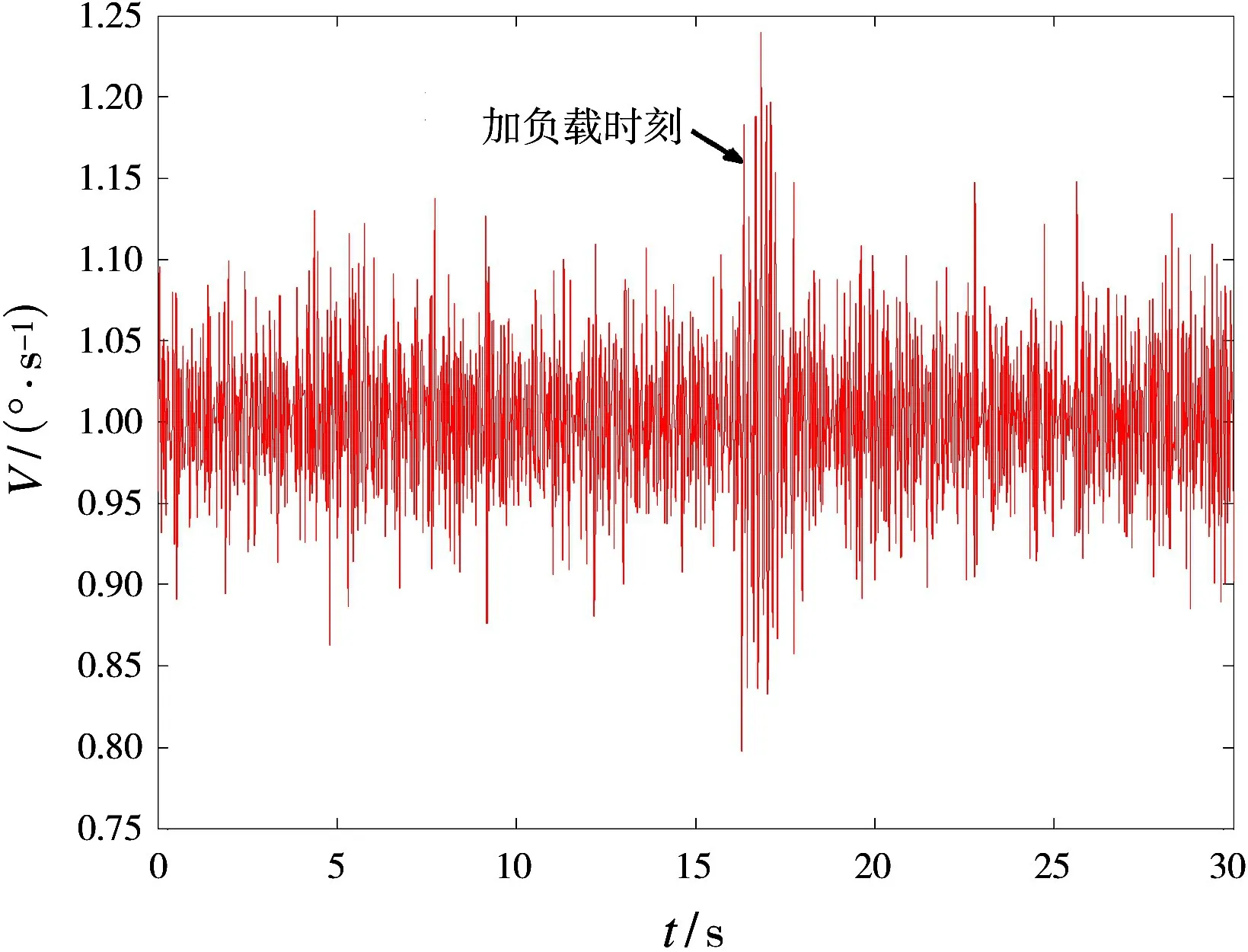
图4 PI控制的速度波动

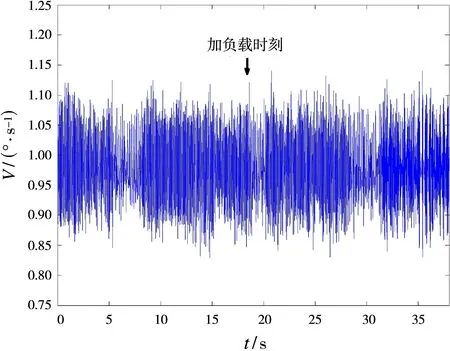
图5 SMC控制的速度波动

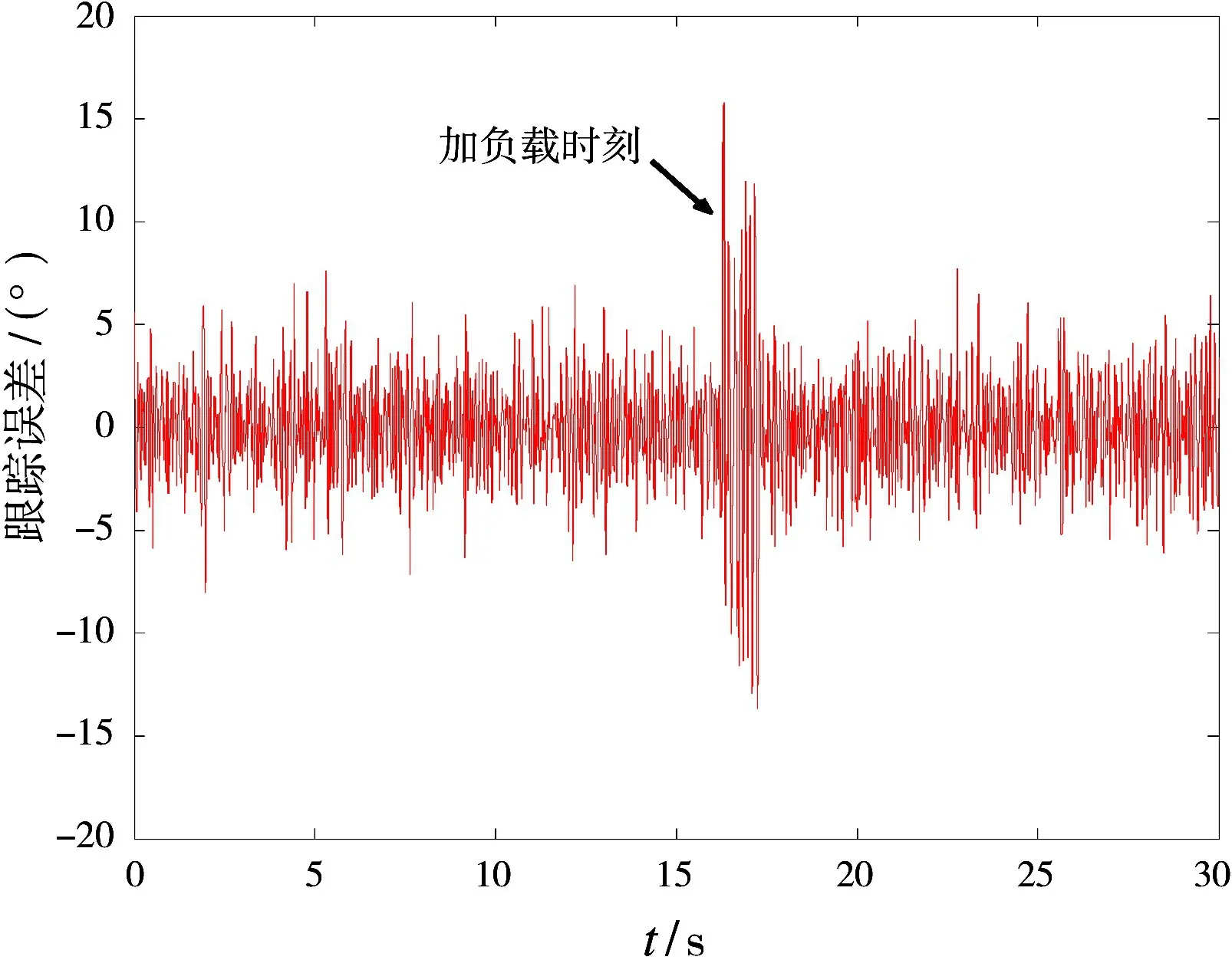
图6 PI控制的跟踪精度

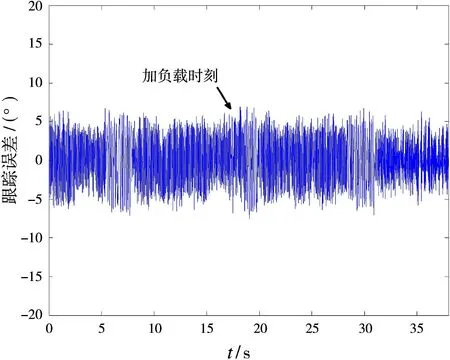
图7 SMC控制的跟踪精度

从实验测试结果可以看出采用PI控制的时候,当外界存在干扰时,稳定平台的速度和跟踪精度都有一定程度上的突变,而滑模控制的鲁棒性较强,速度和跟踪精度在外界干扰情况下几乎保持不变。不足的是,在实际系统实现时,理想的开关特性不可能实现。由于时间延迟、空间滞后等因素的影响,一般很难保证系统完全沿滑模线运动,而是在滑模线两侧来回穿越,从而导致控制不断变化,故SMC控制存在高频抖振现象。抖振现象不仅增加了电机损耗,而且对系统不利。解决办法可以采用高阶滑模控制或将滑模控制与其他鲁棒控制算法相结合的方法来解决。

[1]刘长安.机载稳定平台随动回路控制优化仿真研究[J].计算机仿真,2012,29(6)：63-66.LIU Chang-an.Simulation Research on Servo Loop Control Optimization of Airborne Stabilized Platform[J].Computer Simulation,2012,29(6)：63-66.(in Chinese)

[2]刘颖,周波,方斯琛.基于新型扰动观测器的永磁同步电机滑模控制[J].中国电机工程学报,2010,30(9)：80-85.LIU Ying,ZHOU Bo,FANG Si-chen.Sliding Mode Control of PMSM Based on a Novel Disturbance Observer[J].Proceedings of the CSEE,2010,30(9)：80-85.(in Chinese)

[3]唐茂华.基于直流无刷电机的雷达伺服系统设计[J].雷达科学与技术,2009,7(6)：479-484.TANG Mao-hua.Radar Servo System Design Based on Brushless DC Motor[J].Radar Science and Technology,2009,7(6)：479-484.(in Chinese)

[4]王少威,万山明,周理兵,等.利用蚁群算法辨识PMSM伺服系统负载转矩和转动惯量[J].电工技术学报,2011,26(6)：18-25.

[5]张群,李宏,郑勇.一种新型滑模观测器的永磁同步电动机无传感器控制[J].微特电机,2011(8)：41-43,50.

[6]陈振,耿洁,刘向东.基于积分时变滑模控制的永磁同步电机调速系统[J].电工技术学报,2011,26(6)：56-61.