基于导弹高程的机载红外单站定位方法

蔺建英，袁水平

(解放军91245部队，辽宁葫芦岛125001)

1 引言

在靶场导弹试验中，如果采用一台红外经纬仪对导弹进行测量的同时，还能获得光电经纬仪站点至导弹的斜距参数，就可通过单站定位数学模型计算导弹外弹道，然而，获得精确的导弹斜距参数是十分困难的［1－3］;机载红外经纬仪和其载体飞机的整体费用相比陆上站点要高数十倍，因此，单站定位对于机载光电经纬仪完成导弹远海试验中外弹道测量具有重要意义。

对于在海面上数百米高度飞行的反舰导弹，导弹上安装的无线电高度表的测量精度可达到其飞行高度的百分之一［4］。利用导弹的高程数据、载机(装载红外经纬仪的飞机)姿态角数据、机载红外经纬仪站点高程数据及红外经纬仪测量的导弹方位角和俯仰角数据，通过坐标变换和空间几何关系，可解算得到机载红外经纬仪与导弹之间的斜距。

2 机载红外经纬仪坐标系的定义与关系

在已知载机地理位置数据(可由GPS或北斗卫星定位获得)和导弹相对载机地平坐标系坐标后，可经坐标变换得到导弹在地心坐标系下的位置数据，为简化计算，仅以获得导弹在载机地平坐标系下的坐标作为最终结果。

2．1 坐标系定义

2．1．1 载机地平坐标系的定义

原点O:红外经纬仪水平轴与垂直轴的交点;

OXj轴:过原点的水平面内，指向大地北;

OYj轴:过原点的铅垂线向上;

OZj轴:与OXj轴、OYj轴构成右手直角坐标系。载机地平坐标系OXjYjZj、导弹M与地球椭球相对位置示意图如图1所示。

图1 载机地平坐标系、导弹M与地球椭球相对位置示意图Fig．1 Relative position diagram of airborne horizontal coordinate system，missile M and earth ellipsoid

2．1．2 测量坐标系的定义［5］

过红外经纬仪水平轴与垂直轴的交点并与该设备方位转盘平行的平面，称为大盘平面。载机起飞前使载机纵轴线和横轴线所确定的平面与水平面重合。

直角坐标系

原点O:红外经纬仪水平轴与垂直轴的交点;

OXc轴:在大盘平面内，指向方位转角输出为零的方向，载机起飞前与大地北和载机航向角为0°方向重合;

OYc轴:垂直于大盘平面向上(平行于垂直轴);

OZc轴:与 OXc轴、OYc轴构成右手直角坐标系。

极坐标系

方位角A:由OXc轴起算所旋转的角度，顺时针为正;

高低角E:由大盘面起算所旋转的角度，向上为正;

斜距R:原点O到目标点的直线距离。

2．2 载机地平坐标系与测量坐标系关系

测量坐标系与载机地平坐标系原点相同，OXc轴、OYc轴、OZc轴与 OXj轴、OYj轴、OZj轴相差载机的航向角κ、俯仰角和滚动角γ。航向角κ规定绕轴顺时针方向旋转(从旋转轴正向的一端面对着坐标原点看)为正，俯仰角和滚动角γ以逆时针方向旋转为正。

3 机载红外经纬仪站点与导弹斜距计算方法

已知参数:机载红外经纬仪站点高程H1;导弹高程H2;机载红外经纬仪姿态角即航向角κ、俯仰角、横滚角γ。

求解参数:机载红外经纬仪站点与导弹的斜距。

3．1 导弹在测量坐标系中的坐标

式中，xc，yc，zc为导弹在测量坐标系中的直角坐标;R，A，E分别为导弹相对红外经纬仪站点的斜距、方位角、高低角。

3．2 导弹在载机地平坐标系中的坐标

测量坐标系可以看作是载机地平坐标系经过三个角度的旋转得到的［6］。首先将坐标轴绕OYj轴旋转κ角，使 XjYjZj坐标系变成 XκYκZκ坐标系，然后绕旋转后的Zκ轴旋转角，使XκYκZκ坐标系变成XκYκZκ坐标系，最后绕旋转后的 Xκ轴旋转 γ 角，使载机地平坐标系OXjYjZj与测量坐标系OXcYcZc重合。

当坐标系 OXjYjZj绕 OYj轴旋转 κ角，使OXjYjZj坐标系变成OXκYκZκ坐标系，目标在两种坐标系中的坐标变换:

写成矩阵形式为:

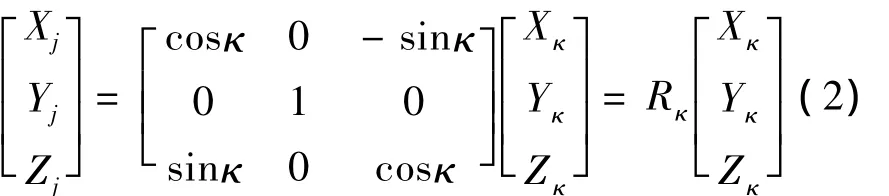
当坐标系 OXκYκZκ绕 OYκ轴旋转 角，使OXκYκZκ坐标系变成 OXκYκZκ坐标系，目标在两种坐标系中的坐标变换:

写成矩阵形式为:

当坐标系 OXκYκZκ绕 OXκ轴旋转 γ 角，使OXκYκZκ坐标系变成 OXcYcZc坐标系，目标在两种坐标系中的坐标变换:

Xκ=xc

Yκ=yccosγ － zcsinγ

Zκ=ycsinγ +zccosγ

写成矩阵形式为:

综合式(4)、式(3)、式(2)和式(1)，得到:

式中，a1=cosκcos ;a2=sin ;a3=sinκcos ;b1= － cosκsincosγ － sinκsinγ ;b2=coscosγ ;b3= － sinκsincosγ +cosκsinγ ;c1=cosκsinsinγ －sinκcosγ ;c2= － cossinγ ;c3=sinκsinsinγ +cosκcosγ 。

3．3 导弹斜距计算方法

图1中，O为载机地平坐标系原点，Or为地球椭球中心，M为导弹位置点，D1、D2分别为O点和M点与Or点连线与海面的交点，D3为由M点向OOr作垂线的交点。则OM=R为导弹斜距，OD1=H1为机载红外经纬仪站点高程，MD2=H2为导弹高程，仅考虑导弹斜距小于数十千米的情况，将地球椭球近似为圆球计算，地球半径OrD1=OrD2=Rr，并设OD3=H3。由图1中几何关系可得:

可导出:

设(xjm，yjm，zjm)为导弹在载机地平坐标系中的坐标，依据式(5)可得:

由式(7)结合图1 可得［7］:

式中，b=2(Rr+H1)［sincos E cos A+coscosγ sin E －cossinγcos E sin A］，式(9)中，除R外均为已知数，解一元二次方程可计算出R;在式(7)中可由yjm≈－(H1－H2)解出R的初值，式(9)中与R的初值接近的为R的真值。

4 单站定位与两站交会定位精度估算及影响因素分析

4．1 已知参数及误差

为进行仿真试验，按照反舰导弹和靶场测控装备可达到的试验条件作如下假定:导弹高程H2=100 m，σH2=1 m;机载红外经纬仪站点高H1=4000 m，σH1=2 m;导弹相对红外经纬仪站点的方位角A=10°、高低角E=－34°、机载红外经纬仪测角精度:σA= σE=0．005°;机载红外经纬仪姿态角:航向角 κ =20°、俯仰角 =7°、横滚角γ=5°，姿态角测量精度(设备可达到且价格可接受的指标):σκ=0．035°、σ =0．02°、σγ=0．02°;Rr=6378137 m。各参数误差是互不相关的。

4．2 单站定位与两站交会定位误差估算

4．2．1 单站定位误差

将式(7)展开，单站定位直角坐标按式(10)、(11)、(12)计算:

将式(7)展开并代入式(8)可得:xjms=(cosκcoscos E cos A － (cosκsincosγ － sinκsinγ)sin E+(cosκsinsinγ － sinκcosγ)cos E sin A)R (10)yjms=(sincos E cos A+coscosγsin E － cossinγcos E sin A)R (11)zjms=(sinκcoscos E cos A － (sinκsincosγ － cosκsinγ)sin E+(sinκsinsinγ － cosκcosγ)cos E sin A)R(12)

根据已知数据和误差，建立10000个随机变量数组的样本模型，用蒙特卡罗仿真估算测量误差，载机地平坐标系斜距R和直角坐标xjms、yjms、zjms的误差σR、σx、σy、σz分布如图2所示。

图2 单站定位误差分布图Fig．2 Single station positioning errors distribution

4．2．2 两站交会定位误差

机载红外经纬仪1参数与单站定位相同，站址坐标取坐标原点x1=0、y1=0、z1=0;机载红外经纬仪2参数作如下假定:站址坐标x2=500m，y2=3900m，z2=8000 m;方位 角 A=290°、高低角E= －34°，航向角κ=30°;其余参数与机载红外经纬仪 1相同。此时，交会角为 70°，定位精度较高［8］。

将式(7)展开，按式(13)、式(14)计算导弹在载机地平坐标系中的方位角Aj、高低角Ej［9］:

两站交会定位直角坐标按式(15)、式(16)、式(17)计算［10］:

根据已知数据和误差，建立10000个随机变量数组的样本模型，用蒙特卡罗仿真估算测量误差，载机地平坐标系直角坐标xjms、yjms、zjms的误差σx、σy、σz分布如图3所示。

图3 两站交会定位误差分布图Fig．3 Double station intersection positioning errors distribution

4．3 定位精度比较

图2 和图3中误差曲线是载机距目标8089 m时的误差曲线，表1中还给出了载机距目标4066 m时的仿真结果。从表1中数据可看出:利用导弹高程经坐标转换计算导弹斜距实现单站定位的误差与两站交会定位误差相当。仿真计算表明:当斜距大于12 km时，两站交会定位精度优于单站定位精度。

表1 单站定位与交会定位精度比较Tab．1 Comparison of positioning accuracy on single station and double station intersection

当机载红外经纬仪用于中靶段脱靶量测量时，由于导弹和靶标在同一帧图像中［11］，影响单站定位精度的误差项中除导弹和靶标高程误差不变外，其他各项误差影响将大大降低，以降低到原误差的1/3～1/5计算，脱靶量测量误差仿真计算结果见表1，从表1中数据看出，脱靶量测量精度高于定位精度一倍以上。

4．4 单站定位精度影响因素分析

4．1节中给出的导弹高程测量精度σH2、机载红外经纬仪站点高程测量精度σH1、机载红外经纬仪测角精度σA、σE和载机姿态角测量精度σκ、σ、σγ皆与导弹定位精度相关，且精度要求较高。除此之外，导弹定位精度还与机载红外经纬仪站点高程与导弹高程之差和与导弹斜距大小相关，斜距测量误差随高程差变化(斜距值固定)仿真曲线如图4(a)，斜距测量误差随斜距值大小变化(高程差固定)仿真曲线如图4(b)，斜距测量误差直接影响单站定位精度，从图4(a)和图4(b)可以看出，采用通过导弹高程计算斜距实现单站定位的方法，必须考虑机载红外经纬仪与导弹的相对位置关系，通过合理布站，可以获得较好的导弹定位精度。

图4 斜距测量误差随高程差和斜距值变化仿真曲线Fig．4 Geodesic distance error simulation curve on difference in elevation and geodesic distance value

5 结论

在导弹靶场试验中，利用靶场遥测设备获得的导弹高程数据，用一台机载红外经纬仪就可实现对导弹的外弹道测量，在与导弹斜距为数千米时，其外弹道测量精度与同等条件下两台机载红外经纬仪交会的测量结果相当，随着载机与导弹斜距的增加，单站定位精度将会低于两台交会定位精度。

［1］ YU Jiaxiang，XIAO Deyun．New approach for ground target location with precision analysis and simulation［J］．Journal of system simulation，2007，(11):4874 － 4876．(in Chinese)余家祥，萧德云．一种新的对地定位方法及其精度分析与 仿 真 ［J］．系 统 仿 真 学 报，2007，(11):4874－4876．

［2］ ZHANG Shiquan，YIN Shimin．Analysis of the location algorithm formobile targets based on mono－station passive infrared method［J］．Laser ＆ Infrared，2011，41(12):1323 －1326．(in Chinese)张世全，殷世民．空中机动目标的红外单站被动定位算法 分 析 ［J］．激 光 与 红 外，2012，41(12):1323－1326．

［3］ LIU Jinmang，LIZhenxing．Algorithm to estimate the parametric trajectory of elevation－only target by single station observation data［J］．Laser ＆ Infrared，2012，42(11):1301 －1305．(in Chinese)刘进忙，李振兴．基于单站测量的纯仰角目标参数航迹滤波方法［J］．激光与红外，2012，42(11):1301－1305．

［4］ WANG Xuan，LIXiaomin．Design of high precision barometric altimeter measuring system in mini UAV［J］．Measurement＆ control technology，2012，(2):12 － 15．(in Chinese)王晅，李小民．高精度小型无人机气压高度测量系统的设计［J］．测控技术，2012，(2):12－15．

［5］ ZHONG Dean，CUI Qinghua．The aerospace observation boatmeasuring＆control communication unit calibration test［M］．Beijing:National Defense Press，2009:12 － 15．(in Chinese)钟德安，崔庆华．航天测量船测控通信设备标校与校飞技术［M］．北京:国防工业出版社，2009:12－15．

［6］ WANG Shugen．The principles and application of photogrammetry［M］．Wuhan:Wuhan University Press，2009:38 －42．(in Chinese)王树根．摄像测量原理与应用［M］．武汉:武汉大学出版社，2009:38－42．

［7］ LIN Minxu，QIAO Yanfeng．Research on single payload air pod target location method［J］．Infrared Technology，2011，(10):593 －597．(in Chinese)林旻序，乔彦峰．单载荷航空吊舱目标定位方法研究［J］．红外技术，2011，(10):593 －597．

［8］ SHIYanzhao，ZHU Xinhua．The study of laying position on basis of photoelectric theodolite［J］．Journal of Detection ＆Control，2009，(12):86 －89．(in Chinese)石彦召，朱新华．基于光电经纬仪的布站研究［J］．探测与控制学报，2009，(12):86 －89．

［9］ LIN Jianying，CHEN Kejian．Aligning error correction method for measurement equipment［J］．Aerospace Control，2009，(2):84 －87．(in Chinese)蔺建英，陈克坚．测量设备站点安装对中误差修正方法［J］．航天控制，2009，(2):84 －87．

［10］ LIN Jianying，CHEN Kejian．The offshoremeasuring platform establish conception［J］．Navy range science，2011，(4):4 －7．(in Chinese)蔺建英，陈克坚．海上靶区建设构想［J］．海上靶场学术，2011，(4):4 －7．

［11］ LIGuoyou，FU Chengyu．Miss distance measurement based on single radar－ photoelectric theodolite［J］．Journal of Projectiles，Rocket，Missile and Guidance，2012，(6):177 －182．(in Chinese)李国友，付承毓．基于单台雷达光电经纬仪的脱靶量测量方法［J］．弹箭与制导学报，2012，(6):177 －182．