基于IDM的需求扰动供应链协调契约研究

杨兴林，朱陈陈

(江苏科技大学经济管理学院，江苏镇江212003)

当今企业为追求更高度的精益化生产来赢取竞争，更注重细化外包分工，加强企业联系，也无形放大了供应链本身的脆弱性，使供应链系统“牵一发而动全身”.如导致日系产品需求急剧萎缩的“钓鱼岛事件”以及让大量香蕉滞烂在港口，20万菲民失业的“黄岩岛事件”等突发事件使得已经协调的供应链系统不再协调.契约作为供应链管理的主要协调机制，如何设计合适的契约来协调供应链，显得格外重要.

比较经典的供应链协调契约如数量折扣契约，回购契约，数量弹性契约以及收益共享契约，在文献［1］中有很好的综述.需求扰动情形下供应链的协调机制大都基于此类经典契约展开，如文献［23］分别用收益共享契约和线性组合契约探讨了需求扰动下供应链协调机制.然而用保险契约来研究供应链的协调问题较少，且大都针对需求不变的情形.如文献［4］用比例型免赔额的保险契约协调了稳态条件下的供应链;文献［5］用固定型免赔额保险机制分析了供应链的最优订货量问题;文献［6］在文献［4］的基础上结合保险契约的性质分析了比例型免赔额保险契约应对突发事件风险下的供应链协调效果.

利益驱动机制是以利益为驱动力的一种相互作用的过程或体制，其关键在于驱动力的来源和相应的实现机制.在供应链企业中，追求自身最大化利润为来源，协调企业间的契约为机制，能使双方均受益且达到双赢效果的机制就是有效的.文献［7］总结出有效的激励契约需满足目标合理性、个体合理性以及激励兼容性3个条件.文中在文献［5］的基础上，研究固定型免赔额保险契约机制.不仅考虑免赔额因素同时还引入赔偿上限因素，基于利益驱动原则，设计出一种体现“射幸”性质的新型保险契约机制.研究表明，考虑赔偿上限因素的保险契约机制可以实现均匀分布市场需求下，具有需求扰动风险供应链的完美协调.

1 模型构建

考虑一个供应商和一个零售商组成的两级供应链系统，销售单周期短寿命产品.零售商不仅在正常的市场需求下面临一定的缺货和滞货风险损失，同时零售商还会遭受到突发事件而引起的需求扰动风险损失.为了规避或减少扰动带来的损失，供应商向零售商提供带有固定免赔额和赔偿上限的保险契约，以突发事件下零售商遭受的缺货和滞货损失应得到的赔偿为依据来计算应收取的保费.同时为满足利益驱动机制，刺激零售商接受此协议，供应商应对零售商进行损失补偿，补偿额应大于收取的保费额，这样才可能让零售商多订货的同时也增加供应商的利润，从而实现供应链的完美协调.

1.1 基本假设及符号

基本假设:①供应商和零售商对待风险的态度都是中性的;②整个供应链上的信息都是透明的，供应链上各个节点企业都知道对方的成本结构和收益信息;③双方都明确市场的需求分布信息，需求扰动风险按已知概率β发生，扰动前后市场需求均符合均匀分布.

符号说明:c为生产成本，w为批发价格，p为售价，由外部市场竞争所决定，v为产品残值，s为销售期内未满足顾客需求的缺货成本，q为订货量，D为随机市场需求，m(x)为稳态市场需求下概率密度函数，M(x)为分布函数，f(x)为扰动市场需求下概率密度函数，F(x)为分布函数，M(x)和F(x)均为可微的单调递增函数，且M(0)=F(0)=0.两种情形下市场需求的期望分别为μm和μf，其中v，w，p，s，c均为外生变量，且满足以下关系:p＞w＞c＞v＞0，w＞s＞0.Π为随机利润，E［·］为期望，r为零售商，s为供应商，sc为整个供应链，i为保险契约.

供应商给零售商提供的保险契约中，T(k，A， B)为应向零售商收取的保费，R为供应商为满足利益驱动原则给予零售商的补偿.契约参数A为供应商承诺的固定免赔额，B为供应商所能接受的最高赔偿上限，k为保费的费率.其中0≤A＜B≤N，k≥1，N为零售商可能遭受的最大损失.突发事件发生后，零售商所面临的损失为Y，零售商接受保险契约后，供应商对零售商的赔偿也就是自己的损失记为I(Y).

随机需求下零售商面临的损失可表示为:

根据保险学的理论，供应商的损失及供应商向零售商收取的保费为:

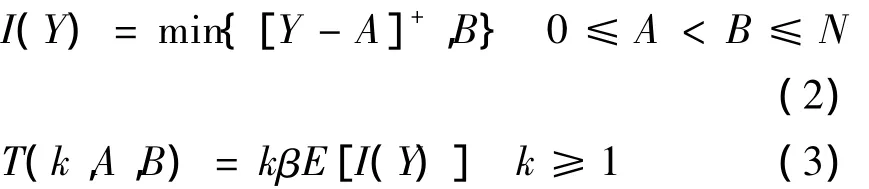
1.2 基于利益驱动机制的新型保险契约下供应链模型

根据利益驱动机制，在文献［5］的基础上提出一种新型的保险契约模式，契约参数为T(k，A，B)和R，其中保费T(k，A，B)由供应商的期望损失进行确定，补偿R由能够协调企业的利益驱动机制确定.由于保险具有“射幸”性质，此处考虑稳态和扰动两种需求状态.故新型保险契约下供应商，零售商及整个供应链的期望利润表示如下:

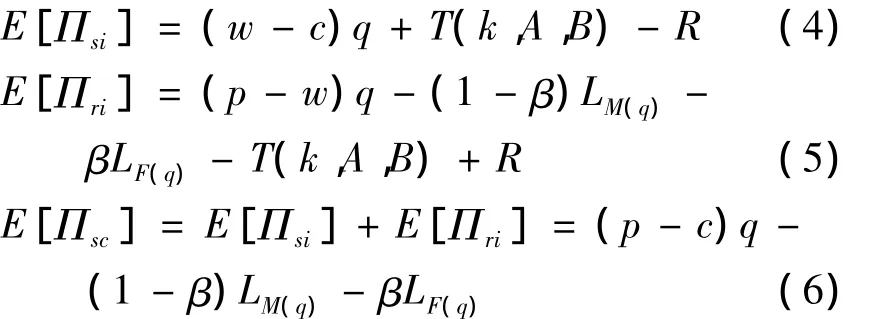
其中LM(q)和LF(q)分别为稳定市场和扰动市场的缺货和滞货损失.

2 新型保险契约下供应链模型求解与分析

2.1 保险契约参数分析

由式(1，2)易知，赔偿上限的取值影响了零售商的订货决策，故文中从以下两种情形进行分类讨论.

情形一:赔偿上限比较小的契约参数分析

当零售商的订货量大于市场需求，即q≥D时

当零售商的订货量小于市场需求，即q＜D时

由式(3，7，8)可得供应商应收取的保费为:

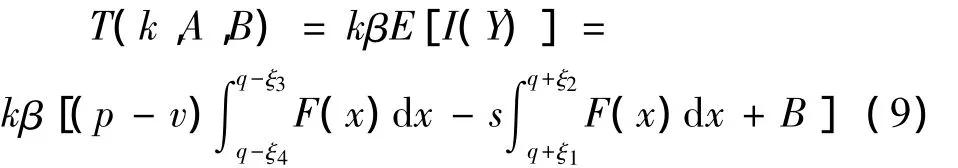
情形二:赔偿上限比较大的契约参数分析

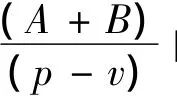
当零售商的订货量大于市场需求，即q≥D时

当零售商的订货量小于市场需求，即q＜D时，表达式与式(8)相同.

设ξ的表示与上面相同，由式(3，8，10)可知供应商收取的保费为:

总结情形一与情形二可知性质1:

性质1:1)保险费函数是免赔额的单调减函数，是赔偿上限凹的单调增函数;

2 )零售商的期望利润是免赔额的单调增函数，是赔偿上限凸的单调减函数;

3 )供应商的期望利润是免赔额的单调减函数，是赔偿上限凹的单调增函数.

2.2 均匀分布市场需求下新型保险契约协调分析

文中假设市场需求满足均匀分布.文献［8］针对无利润组织或政府机构设计了一种保险机制，对于决策者来说如何使用保险策略来决定供应链扰动风险下最优的库存水平，并对均匀分布和正态分布两种市场需求下进行数值分析，得知均匀分布的适用范围比正态分布更广.文献［9］研究了在均匀分布需求下，如何使用奖励和惩罚的双重契约来达到供应链的渠道协调.这也为文中的模型，假设市场需求分布满足均匀分布函数提供了理论依据.文献［5］的保险模型对市场分布为均匀分布的情形协调较困难，这也为文中的假设研究提供了理论研究意义.而在实际的生产中，产品生命周期比较短，可以根据以往的市场需求量推断出大致的需求区间产品，例如圣诞树，农业种子，重大节日纪念品等.为了简化模型，而又不失一般性，文中根据文献［10］的思想，令稳态的市场需求服从［0，b0］的均匀分布，突发事件发生后市场需求服从［0，b1］的均匀分布，且分布函数M(b0)=F(b1)=1.

普通批发价格下，供应商和零售商的期望利润为:

令qr，q*表示普通批发价格契约下零售商和整个供应链的最优订货量.根据文献［5］的定理，可知qr＜q*.也就是说由于双重边际效应的存在(w＞c)，零售商的最优订货选择与整个供应链的最优订货选择无法一致.

由式(6，12)易得:

情形一:赔偿上限比较小的保险契约协调分析

根据式(9)，均匀市场需求下供应商应收的保费以及零售商接受契约后的期望利润对订货量求一阶导数可知:保费只是关于保险参数的恒定值，不是有关订货量q的函数表达式，导致了零售商不管接受保险契约与否，都不会改变初始的订货量决策.其实从整个过程来看，零售商若接受此种情况下的契约模式，只要交一定数量的保费，就会小于供应商给予零售商的补偿，从整个过程而言，供应商是不断损失的，而零售商是不断获利的.这不符合利益驱动机制的激励兼容性条件，供应商也不会提供这种契约模式给零售商.

情形二:赔偿上限比较大的保险契约协调分析

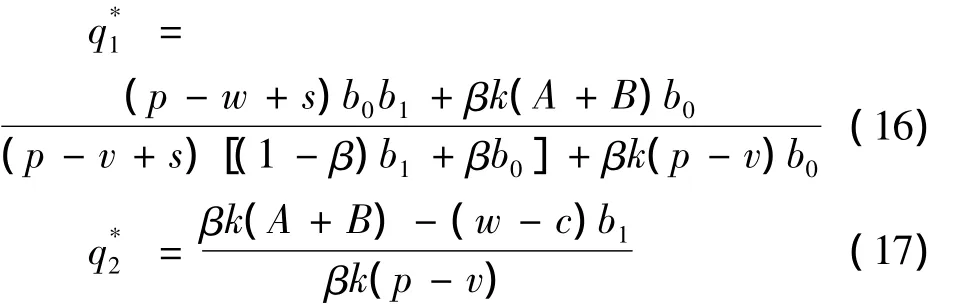
性质2:1)零售商的期望利润关于订货量是凹的，供应商的期望利润关于订货量是凸的，且协调的最优订货量q存在.

由性质2可知，接受契约后零售商的最优订货量大于初始的订货量，即qr＜q，而整个供应链的最优订货量为q*.若要想达到供应链的协调，可令q*=q，找出契约参数应满足的关系.由式(15，16)得:

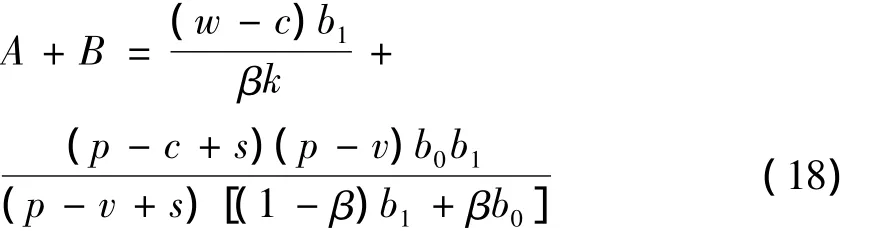
且赔偿参数之和存在一定范围，即:

同时为了满足利益驱动机制，由式(4，5，12，13，16)可得补偿参数的范围:

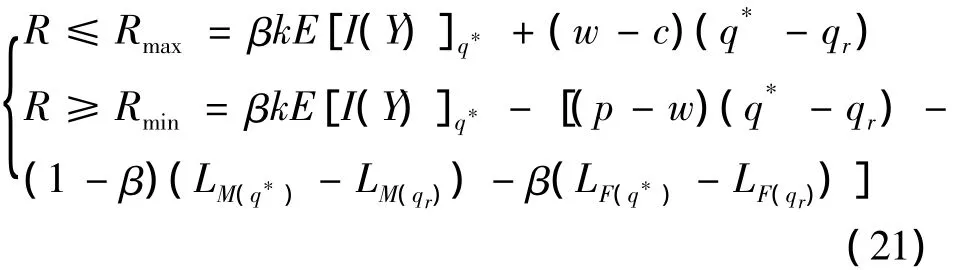
综上可以得到性质3:

性质3:1)当供应商给予零售商的契约参数中的赔偿上限比较小时，供应链无法达到协调的条件，且供应商不会对零售商提供此种形式的契约.

2 )当供应商给予零售商的契约参数中的赔偿上限比较大，且契约参数满足一定条件时，供应链可以达到均匀分布条件下具有扰动风险的完美协调.

3 数值分析

假设有关产品的参数设置如下:

市场上单位产品的零售价格p=10，供应商给予零售商的批发价格w=8，产品的成本c=7，产品缺货的情形下对零售商的商誉损失s=6，产品滞货的情形下产品的残值v=5，稳态的市场需求最大值b0=500，突发事件下市场需求的最大值b1=1000，突发事件发生的概率β=0.3.初步选定基准的契约参数(k，A，B)为(2.1，500，3500)，R∈(570，585).

3.1 参数对于最优订货量与最小订货量的影响

由最优订货量和最小订货量的表达式可以看出其值与保费参数有关，与补偿参数无关.而对于保费参数，虽然免赔额和赔偿上限都对上述订货量起到正相关的影响，但起决定作用的是赔偿参数之和，也就是免赔额与赔偿上限之和A+B的大小，即使免赔额增大，订货量的大小也不一定改变.所以对赔偿参数之和以及费率对最优订货量和最小订货量进行敏感性分析.订货量的变化如图1，2.

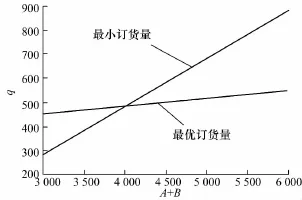
图1 A+B对订货量的影响Fig.1 Effect of A+B on order quantity

图2 k对订货量的影响Fig.2 Effect of k on order quantity

由图1，2可以看出最优订货量和最小订货量都随着赔偿参数和费率的增加而增加，只不过两个参数对于最优订货量影响不是很敏感，而对于最小订货量影响很大.因此得到性质4.

性质4:1)最优订货量或最小订货量取决于赔偿参数之和，与赔偿参数无直接关系.

2)最优和最小订货量都随着赔偿参数之和与费率的增加而增加，但两因素对最优订货量影响不大;最小订货量随着赔偿参数之和均匀增加，而随着费率的增加，最小订货量增加的速率先急剧增加然后慢慢放缓，直至趋于水平线.

3.2 参数对于保费的影响

通过给定基准的契约参数(k，A，B)为(2.1，500，3500)，讨论当一种变量保持不变，另外两种变量对保费的影响.其相应的变化趋势如图3～5.

图3 T与A，B的关系Fig.3 Relationship of T between on A and B

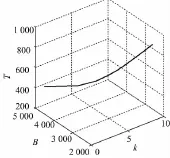
图4 T与k，B的关系Fig.4 Relationship of T between on k and B

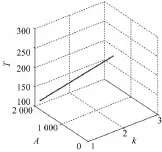
图5 T与k，A的关系Fig.5 Relationship of T between on k and A

由图3可以看出保费随着免赔额的增加而逐渐减少，随着赔偿上限的增加而逐渐增大;由图4可知保费随着费率的增加而逐渐增加，随着赔偿上限的增加而逐渐减少，变化的速率比较明显;由图5可知保费随着费率的增加而增加，随着免赔额的增加而减少.区别在于保费对变量变化的速率的差异，由此得到性质5.

性质5:1)当费率保持不变时，保费随着免赔额的增加而出现凸的递减趋势，随着赔偿上限的增加而出现凸的递增趋势，且变化比较迟缓.

2 )当免赔额保持不变时，保费随着费率的增加而出现凹的递增趋势，随着赔偿上限的增加而出现凸的递增趋势，且变化速率都是先急剧增大然后在逐渐放缓.

3 )当赔偿上限保持不变时，保费随着费率的增加而增加，随着免赔额的增加而出现递减趋势，且变化比较均匀.

4 结论

文中基于利益驱动机制，着眼于在均匀分布市场需求下，设计出一种新的保险契约，来协调具有扰动风险的供应链.通过对契约参数的分类讨论，得到如下结论:

1 )不管赔偿上限B有无限制，零售商的期望利润都是随着免赔额的增加而增加，随着赔偿上限的增加而减少，供应商的利润与之相反;

2 )供应商提供给零售商的契约参数赔偿上限应足够大，且契约参数需满足一定的条件可以实现均匀分布市场需求下，具有需求扰动风险的供应链完美协调;

3 )供应商在制定契约参数时，为追求最大利润，在满足利益驱动原则下应尽可能地扩大最优订货量和最小订货量的差距.

References)

［1］ Cachon G P.Supply chain coordination with contracts.In:Graves S，de Kok T Eds.Handbooks in operations research andmanagement science:supply chain management［M］.The Netherlands，Amsterdam:Kluwer，2003.

［2］ Zhang W，Fu J，Li H，Xu W.Coordination of supply chain with a revenue-sharing contractunder demand disruptionswhen retailers compete［J］.International Journal of Production Economics，2012，138(1):162179.

［3］ Lei D，Li J，Liu Z.Supply chain contracts under demand and cost disruptions with asymmetric information［J］.International Journal of Production Economics，2012，139(1):116126.

［4］ Lin Z，CaiC，Xu B.Supply chain coordination with insurance contract［J］.European Joural of Operational Research，2010，205(2):339345.

［5］ 林志炳，张岐山，李美娟.附免赔额保险协议下的供应链协调分析［J］.中国管理科学，2009，17(6):5762.

Lin Zhibing，Zhang Qishan，Li Meijuan.Supply chain coordination analyis with deductible insurance contract［J］.Chinese Journal of Management Science，2009，17 (6):5762.(in Chinese)

［6］ 郑奇威，季建华，陈娟.突发事件风险下保险合同对供应链的协调研究［J］.科学技术与工程，2012，12 (8):18411845.

Zheng Qiwei，Ji Jianhua，Chen Juan.Supply chain coordiantion with insurance contract under demand disruption［J］.Science Technology and Engineering，2012，12 (8):18411845.(in Chinese)

［7］ Chen P.Portfolio setting of insurance contractswhen facing a retailer with unknown risk pref-erence［D］.Taiwan:National Central University，2011.

［8］ Lodree E J，Taskin S.An insurance risk management framework for disaster relief and supply chain disruption inventory planning［J］.Journal of the Operational Research Society，2008，59(5):674684.

［9］ 李凯，张迎冬，严建援.需求均匀分布条件下的供应链渠道协调:基于奖励与惩罚双重契约［J］.中国管理科学，2012，20(3):131:136.

Li Kai，Zhang Yingdong，Yan Jianyuan.Supply chaincoordination under uniformly distributed market demand:A dual contract based on both bonus and penalty［J］.Chinese Journal of Management Science，2012，20 (3):131:136.(in Chinese)

［10］ 马利军.具有公平偏好成员的两阶段供应链分析［J］.运筹与管理，2011，20(2):3743.

Ma Lijun.Supply chain analysiswith fairness preference agent［J］.Operations Research and Management Science，2011，20(2):3743.(in Chinese)