玻色超流体中的准粒子激发与稳定性

贺丽

(江苏科技大学张家港校区基础教学部，江苏张家港215600)

超流是凝聚态物理中一类重要的宏观量子现象，其本质是大量粒子在集体运动中所表现出的相位相干性.在三维玻色系统中(如液氦、冷原子气体等)，超流总伴随着玻色-爱因斯坦凝聚的发生［1-3］，而博戈留波夫方法是理解这类物理系统最基本的理论工具.该方法不仅适用于平衡态性质的描述，还可以用于处理非平衡的稳态.文中利用博戈留波夫方法求解了以一定速度流动的玻色超流体的准粒子谱，并根据色散关系的正定性给出了超流稳定性条件.当体系具有伽利略不变性时，该条件即等价于朗道判据.而当伽利略不变性不满足时，朗道判据不再成立，超流稳定性只能通过准粒子的激发谱来判断.我们通过具体模型的计算，分别讨论了上述两种不同情形下的超流临界速度.

1 流动状态下的准粒子激发

从描述相互作用玻色系统的一般性哈密顿量出发，其二次量子化形式为

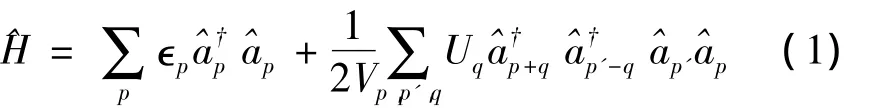
考虑玻色超流体以速度v流动，有宏观数目为N0个的粒子占据在动量为p0的态上，形成玻色爱因斯坦凝聚，p0满足(∂p∈p)p=p0=v.由于相互作用造成的粒子间的散射，即使在零温，凝聚粒子数N0也会小于系统总粒子数N，而占据p≠p0态的非凝聚粒子被称为量子亏缺(quantum depletion).亏缺部分与凝聚部分之和满足总粒子数守恒.

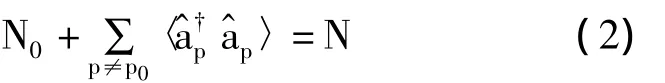
文中仅限于讨论零温的情况，即亏缺部分全部由量子涨落提供，而没有热激发的贡献.

当相互作用较弱时，可以用博戈留波夫理论处理该系统.由于凝聚粒子数目为宏观量级N0≫1，可以合理地将动量p0对应的算符用常数来代替，ap0≈a≈，而非凝聚部分的贡献则可视为涨落效应，对于p≠p0的算符保留至二阶，可将哈密顿量近似为［1］:

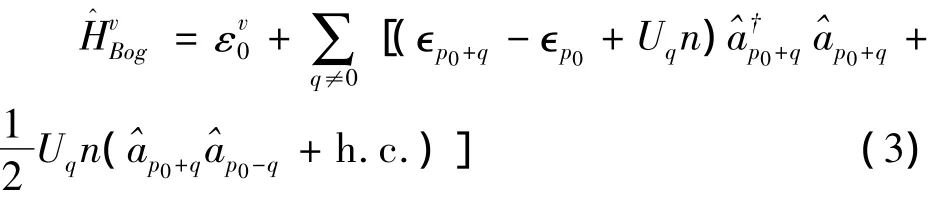
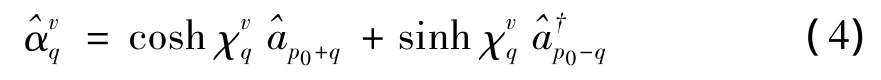
当正则变换系数满足下述关系时，

哈密顿量可以写为对角化形式:

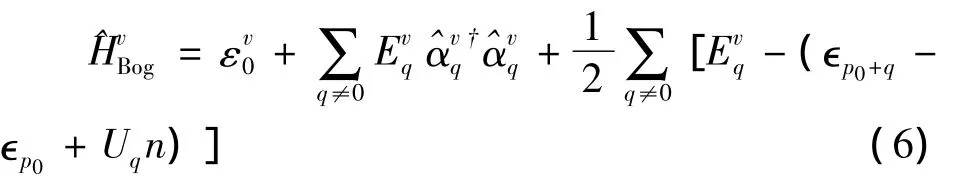
式中准粒子能量为:

式(4～7)实际上是玻色超流体博戈留波夫理论的一般性结果，当取v=0时(即p0处于能谱∈p最小值点时)该结果对应于平衡态的情形［1］，而当v为有限大小时则描述的是流速恒定的稳态.

在准粒子表象下，容易求得非凝聚原子(即量子亏缺)的数目，当不产生准粒子激发时，可以得到

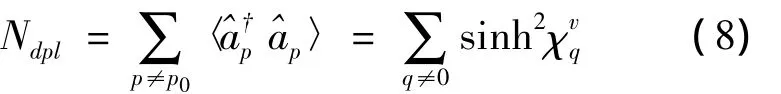
只要相互作用足够弱，非凝聚粒子数目总是占很小的比例，即Ndpl≪N，这一关系保证了博戈留波夫前提假设的自洽性.

2 超流稳定性

稳定的超流态可以无阻尼的流动，这种情形对应于准粒子的真空态.当体系出现准粒子激发时，准粒子与外部(包括器壁、杂质等)的碰撞会造成系统能量和动量的损失，从而产生耗散［23］.因此，超流的稳定性要求准粒子能谱必须是恒正的，即稳定性条件可一般写为:

显然，当流速v足够大时，上述条件必然会被破坏，故存在一个超流稳态的速度上限，即临界速度vc.

2.1 伽利略不变性与朗道判据

当单粒子能谱取为通常的自由原子的色散关系∈p=p2/(2m)时，体系的流速与凝聚动量满足v= p0/m，而公式(7)中的准粒子能量可简化为:

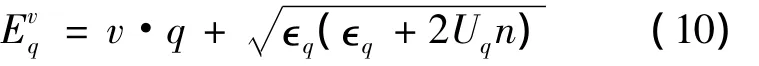
显然，对于给定的流速v，最容易造成不稳定的动量出现在与v相反的方向，因此超流稳定条件又可进一步写为:

这正是最早由朗道提出的超流判据［23］.与前面的微观理论推导不同，朗道在提出该判据时直接采用了系统具有伽利略不变性这一特征，从而得到了流动体系与静止体系的准粒子谱关系为E= E+q·v，即公式(10)的结果.当朗道判据取等号时所对应的速度即为该系统的超流临界速度vc.

图1为当系统具有伽利略不变性时，玻色超流体在不同流速下的准粒子谱.通过两个实例给出了当相互作用势取不同形式时流动状态下的准粒子色散关系及相应的临界速度.图1a)取接触相互作用势Uq=U0，超流临界速度即为声子的速度，vc=c≡;图1b)取含动量线性依赖的相互作用势Uq=U0+U'q，此处取U'=0.98)当相互作用满足1＜U'＜2时，准粒子的色散谱会出现一个能量局域极小的旋子激发，此时超流临界速度由旋子决定，vc=Δrot/qrot，其中，qrot=［3mnU'+/2和Δrot= n分别为静止情况下的旋子动量和旋子能隙.

图1 玻包超流体在不同流速下的准粒子谱Fig.1 Quasi-particle spectrum of bosonic superfluid w ith different velocity

需要强调的是，在这两个例子中朗道判据与超流稳定性条件一致是单粒子哈密顿量满足伽利略不变性的结果.当这一前提条件不成立时，朗道判据原则上不再适用，超流的稳定性条件以及临界速度只能由更为普适的公式(9)给出.

2.2 存在自旋－轨道耦合时的超流临界速度

近来，具有自旋-轨道耦合效应的玻色-爱因斯坦凝聚成为冷原子物理中的一个研究热点［4-5］.在这个系统中，由于自旋自由度与轨道自由度之间的纠缠，伽利略不变性是不被满足的.在目前所广泛采用的实验方案中，自旋-轨道耦合效应是借助拉曼光的双光子跃迁来实现的［6-8］.通过这种耦合光场作用，在沿拉曼光方向上最低能带的单粒子色散关系被调制为

式中:kr为反冲动量;Ω为拉曼耦合强度;δ为拉曼失谐.实验中这3个量都是连续可调的参数，在不同参数条件下，可以人为地控制单粒子能谱的色散行为.这里重点关注物理上最有兴趣的一种情况，即Ω=2k/m，δ=0的情形，此时单粒子能谱在小动量时呈现出四次方的色散关系(选择适当的能量零点)，

超流稳定性的必要条件是沿凝聚动量反方向传播的声子激发能量恒正，由此临界失稳的凝聚动量大小为p0c=(6U0nmk)1/4.再代入速度动量关系，即可求得体系的超流临界速度

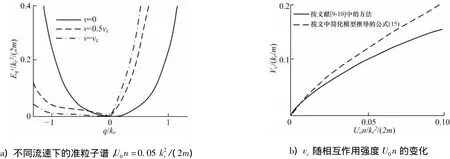
图2 自旋－耦合玻色气体的超流稳定性Fig.2 Superfluid stability of Bose gasw ith spin-orbit coupling

这个有限大小的临界速度从一个侧面说明了朗道判据的失效.这是因为，对于静止的凝聚体而言(p0=0)，准粒子色散谱在长波极限下的声速为零，即min(∂p∈p)=0，如果按朗道判据则会给出临界速度为零的错误结论.这里朗道判据不适用的物理原因正是由于体系不具有伽利略不变性导致的.

在上述简化模型的处理中，假定了决定体系稳定性的准粒子激发总是出现在由公式(14)描述的小动量区间内，而高阶修正可以忽略不计，此外也没有考虑相互作用势对动量的依赖关系.计入这些因素后，可以发现，只有当相互作用较弱时超流的稳定性才是由声子决定的［9］，而当相互作用较强时最先失稳的是旋子激发.采用文献［9-10］中给出的方法，在不做简化的情况下计算了临界速度随相互作用强度的变化关系，如图2b)所示.可以看到，从简化模型推出的公式(15)在弱相互作用条件下定量上符合得很好，这个公式为之前的数值计算提供了解析上的渐进形式.

3 结论

文中用博戈留波夫方法推导了流动状态下玻色-爱因斯坦凝聚的准粒子激发谱，并根据激发谱的正定性要求得到了超流稳定性条件.当体系哈密顿量满足伽利略不变性时，该稳定性条件与朗道判据等价;而当体系不具有伽利略不变性时，朗道判据不再适用，超流的稳定性则需根据准粒子谱来确定.作为一个实例，计算了存在自旋-轨道耦合时玻色气体在一种特殊情况下的超流临界速度，并推导出临界速度在相互作用较弱时的渐进表达式.

References)

［1］ 费特，瓦立克，陈俊文，等译.多体系统的量子理论［M］.北京:科学出版社，1984:618-634.

［2］ Pitaevskii L P，Stringari S.Bose-Einstein condensation［M］.Oxford:Oxford University Press，2003:63-82.

［3］ Pethick C J，Smith H.Bose-Einstein condensation in dilute gases［M］.Cambridge:Cambridge University Press，2001:290-296.

［4］ ZhaiH.Spin-orbit coupled quantum gases［J］.Int JMod Phys B，2012，26:1230001.

［5］ Galitski V，Spielman IB.Spin-orbit coupling in quantum gases［J］.Nature，2013，494:49-54.

［6］ Lin Y J，Jiménez-García K，Spielman IB.A spin-orbit coupled Bose-Einstein condensate［J］.Nature，2011，471:83-86.

［7］ Zhang JY，Ji SC，Chen Z，et al.Collective dipole oscillations of a spin-orbit coupled Bose-Einstein condensate［J］.Phys Rev Lett，2012，109(11):115301.

［8］ Wang P，Yu ZQ，Fu Z，et al.Spin-orbit coupled degenerate Fermi gases［J］.Phys Rev Lett，2012，109: 095301.

［9］ Ozawa T，Pitaevskii L，Stringari S.Supercurrent and dynamical instability of spin-orbit-coupled ultracold Bose gases［J］.Phys Rev A，2013，87:063610.

［10］ ZhengW，Yu ZQ，Cui X，etal.Properties of Bose gaseswith Raman-induced spin-orbit coupling［J］.J Phys B，2013，46:134007.