推土机工作装置的仿真和优化

李绪永, 孟令韩， 王树凤

(1.山东理工大学 交通与车辆工程学院, 山东 淄博 255091； 2.济南交通高级技工学校， 山东 章丘 250200)

大型推土机工作条件恶劣，其零部件对耐磨性、疲劳强度和冲击韧性要求较高.推土机工作装置要完成松土、铲土、短距离运送等工作，受力大，各构件相对运动复杂，这就对推土机工作装置的可靠性研究提出了较高的要求[1-2].国内已经对此进行了很多相关研究，青岛大学的林晓磊等对推土机工作装置的某铰接点处易发生断裂的实际情况进行了ADAMS仿真，但未进行优化[3]；吉林大学的叶兰成利用ADAMS对工作装置进行了建模，并进行了运动学、动力学及有限元分析，然后通过经验进行了优化，却没有进行样机的检验[4];吉林大学的赵雪莉对工作装置用MATLAB工具进行了数学建模和优化，并用ADAMS的建模仿真工具进行了检验，虽然有比较完整的建模仿真优化，但缺少较多的实际工况的仿真验证[5].本文以某推土机工作装置为研究对象，针对四种常见工况进行虚拟样机的仿真分析，根据分析结果对不理想的参数进行优化.

1 推土机工作装置的结构与受力分析

1.1 推土机工作装置的结构分析

图1 推土机工作装置实物图

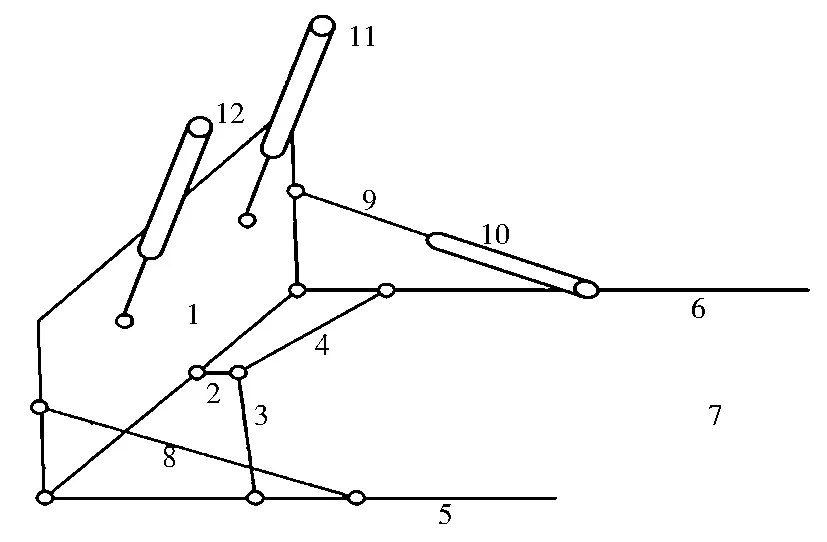
1.推土铲；2.连接基座；3.左横拉杆；4.右横拉杆；5.左顶推梁；6.右顶推梁；7.机架；8.斜撑螺杆;9.侧倾杆；10.侧倾油缸；11.右举升缸；12.左举升缸图2 推土机工作装置结构简图

图1所示为推土机工作装置的实物图，图2为其结构简图.推土机工作装置主要由举升机构和侧倾机构组成.举升机构由举升杆、举升缸、推土铲、顶推梁、机架组成.举升缸(杆)与推土铲以球铰的形式链接，另一端以球铰的形式连接在机架上.顶推梁两端都以球铰的形式连接在推土铲和机架上.工作时，举升缸提供动力，使得推土铲举升，同时顶推梁绕机架转动，实现推土铲的举升[6-7].

侧倾机构由侧倾杆、侧倾油缸、斜撑螺杆、推土铲、左右横拉杆、左右顶推梁、机架组成.侧倾油缸(杆)一端以球铰接的方式和右顶推梁相连接，另一端与推土铲以球铰的方式连接.水平横拉杆一端用球面副与连接基座相连接，另外一端用球面副与顶推梁相连接. 工作时，侧倾油缸推动侧倾杆运动，以提供偏转的动力，最终实现推土铲的侧倾. 各个部件之间连接方式如图2所示(水平横拉杆主要起平衡力矩的作用).

1.2 推土机工作装置不同工况下的动力学分析

推土机在工作过程中，要完成松土、铲土、短距离运送等工作，本文根据其工作情况，对推土机四种工况下的工作装置进行动力学分析，具体情况如下：

1)上升工况

上升工况即推土铲从最低点上升到最高点的工况，此时举升缸以及举升机构起作用，除物料的重力外，没有外力作用.在此假设物料在举升过程没有洒落，也即物料的重力不变.

2)侧倾工况

侧倾工况即推土铲从最右倾位置旋转到最左倾位置，此时侧倾缸以及侧倾机构起作用，此过程也是空载，没有外力作用.

3)运土前工况

运土前工况即铲土结束以后，推土铲满载从铲土最低点上升到地平面位置的过程.此过程满载，即外力只受到满载的土料的重力G的作用.推土铲上满铲土料重力大小可由以下公式计算得到：

G=ρ·V'max·g

(1)

式中：ρ为土料的密度；V'max为推土铲的满铲容量；g代表重力加速度.

4)铲土工况

铲土工况即推土铲从地平面位置下铲到达最低点位置的过程.此过程推土机在匀速前进中铲土，实现了空载至满载即土料实现了从0到G的转变，该工况结束时刻推土铲的受力如图3所示.图3中，A、B点分别代表举升缸及顶推梁与推土铲的铰接点，C、D点分别代表土料重心垂线与地面及推土铲的交点，E、O点分别代表推土铲的两个顶点.

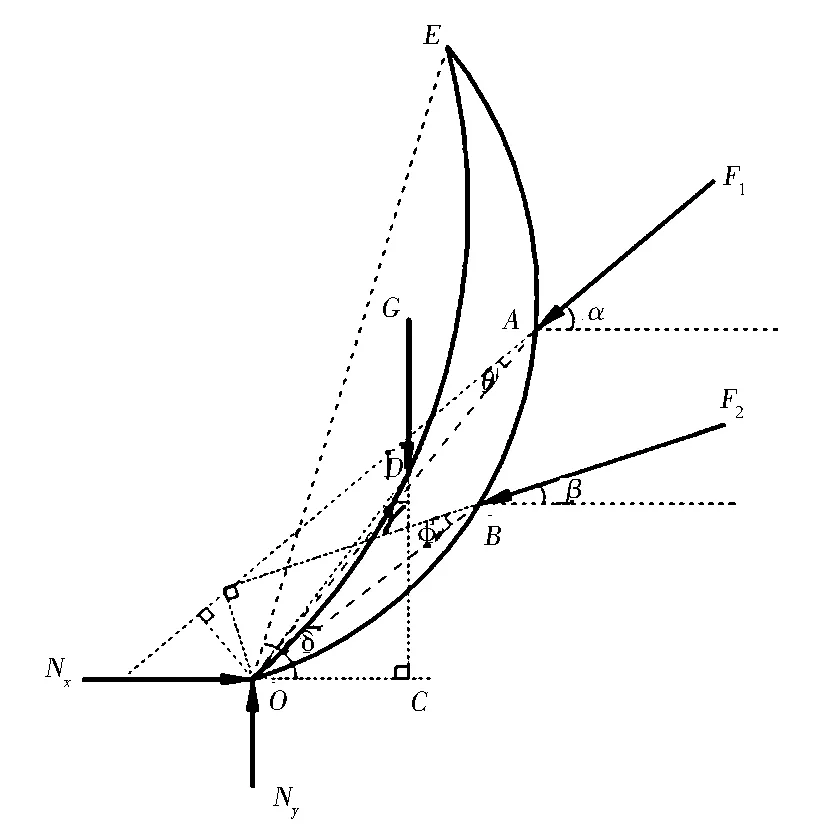
图3 推土铲在铲土工况的受力图

根据O点的力矩平衡得

G·lOD·sinγ-F1·lOA·sinθ-

F2·lOB·sinφ=0

(2)

根据力的水平和垂直方向平衡得

Nx-F1cosα-F2cosβ=0

(3)

Ny-F1sinα-F2sinβ-G=0

(4)

又有

F1=P·S

(5)

由该图形的几何关系知

θ=∠AOC-α=δ-α-∠AOE

(6)

φ=∠BOC-β=δ-β-∠BOE

(7)

γ=90°-∠DOC=90°-α+∠DOE

(8)

式中：F1为举升缸的液压力；F2为顶推梁力；G为铲上的土料重力；Nx为地面水平反力；Ny为地面垂直反力；P代表举升缸内的油压；S代表举升缸内的横截面积；α代表举升缸与水平面的夹角；β代表顶推梁与水平面的夹角；γ代表OD与数值方向的夹角；θ代表OA与F1延长线的夹角，φ代表OB与F2延长线的夹角；δ即∠COE代表前倾角.lOA,lOB,lOD,α，β，δ，∠AOE，∠BOE，∠DOE是几何数据，G在前面已经求得，从而可以由公式(1)～(8)求得F2,Nx,Ny.

2 推土机工作装置的建模与仿真

2.1 工作装置的建模

通过以上对某推土机工作装置的结构和受力分析，使用虚拟样机软件ADAMS对其进行建模，建模过程如下：

1)首先根据图1的模型及实车尺寸确定各主要关键点的坐标，利用Point工具将这些点标记在相应的坐标上；然后利用几何建模工具箱中的Link工具画出顶推梁，用Cylinder工具画出液压缸和横拉杆等，用Polyline工具将推土铲的截面画出来，并用Extrusion工具将截面拉伸成为立体的推土铲.

2)在相应的铰接点处添加球形副或转动副等，并在相应的液压缸上添加移动副.

3)针对不同的工况，分别对液压缸赋予相应的运动，并对推土铲赋予相应的外力.

4)进行模型验证，验证结果显示模型拥有13个部件，14个球形副，2个转动副，1个圆柱副，3个驱动和若干个外力(外力的数量视具体工况而定)，以及0个自由度.

最终得到的推土机工作装置模型如图4所示.

图4 工作装置虚拟样机模型

2.2 工作装置的仿真分析

通过对四种常见工况进行仿真，观察其运动过程，进行干涉分析，可判断结构是否符合预期的要求、运动过程中有无参数的突变等.仿真过程中需要测量的参数有：液压缸伸长量、推土铲高度、前倾角(即铲刀横截面所在弧线的内弦所在直线与地平面的夹角)、侧倾角(即铲刀刀刃所在直线与地平面的夹角)，另外还需要测量各构件的受力大小，判断是否受力过大、受力不平衡等.

图5～图9为推土机工作装置的运动学仿真结果，其中图5和图6是举升工况和侧倾工况仿真开始和结束时刻的模型图(运土前工况和铲土工况的效果图大体同举升工况一致).图7～图9是举升工况3个参数的变化曲线，从图7中可以看出，液压缸的伸长量最长是107. 5cm，最短是18.03cm.从图8可以看出，推土铲的最高点坐标是57.99cm，最低点坐标是-54.9cm，与实际样机的误差都控制在0.1cm以下.观察图9可知，推土铲的前倾角从82.4°变化到68.04°，即该推土铲能实现从最低点的82.4°到最高点的68.04°的转变，该角度变化范围满足工程要求的68°的切削角度范围和84°的铲削角度范围，适合铲削和运土.

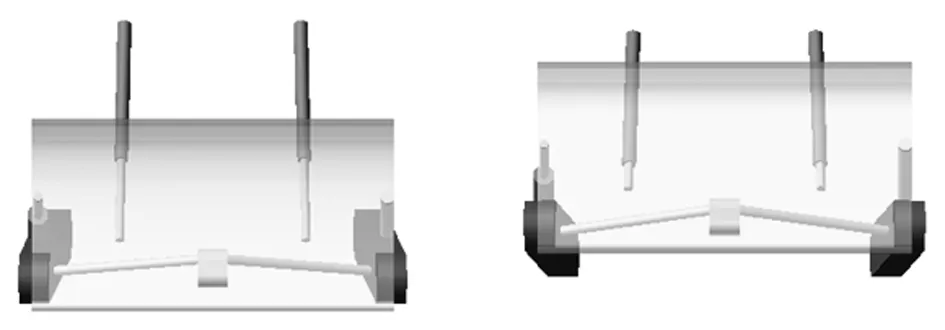
(a)开始时的状态(b)结束时的状态图5 举升过程的前视图

(a)开始时的状态(b)结束时的状态图6 侧倾过程的前视图

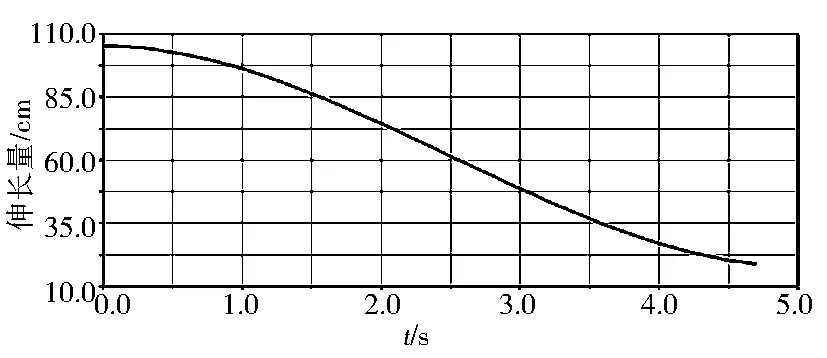
图7 举升缸伸长量变化曲线

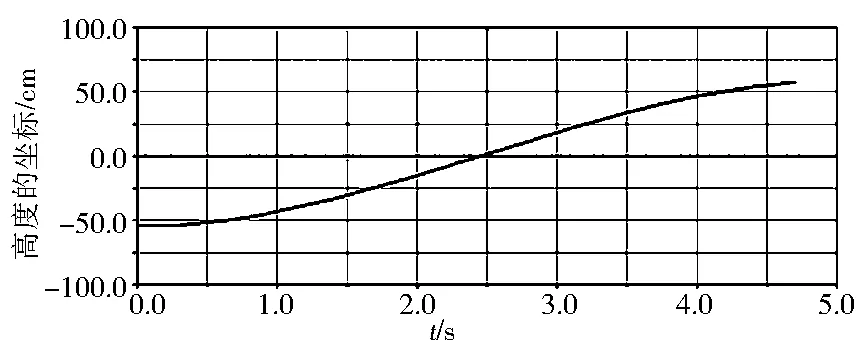
图8 推土铲高度坐标的变化曲线

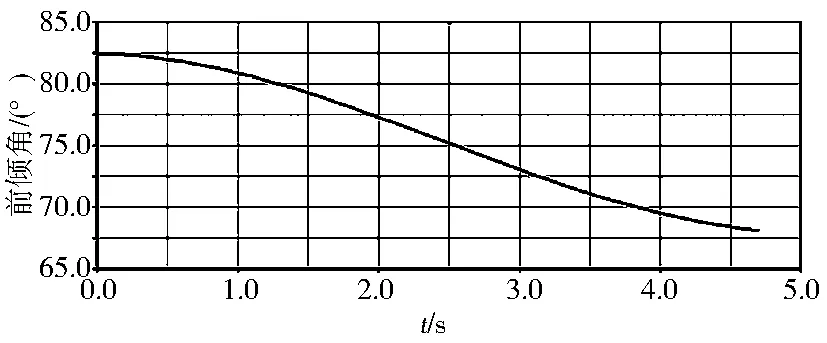
图9 推土铲前倾角变化曲线

测量推土铲上各铰接点的受力，包括推土铲与左右举升缸杆的铰接点、与斜撑螺杆和侧倾缸(杆)的铰接点、与左右顶推梁的铰接点这6个点，会发现各个工况下都存在左右受力不等的情况.机体左右受力不平衡会造成机身连接处受到力矩的作用，若力矩过大会造成较大的安全隐患，因此将力差作为研究对象并进行如下分析.

定义subtract_1为推土铲与左右举升缸杆的铰接点的力差，subtract_2为推土铲与斜撑螺杆以及侧倾缸杆的铰接点的力差，subtract_3为推土铲与左右顶推梁的铰接点的力差，则4个工况仿真过程的3种力差变化曲线如图10～ 图13所示.

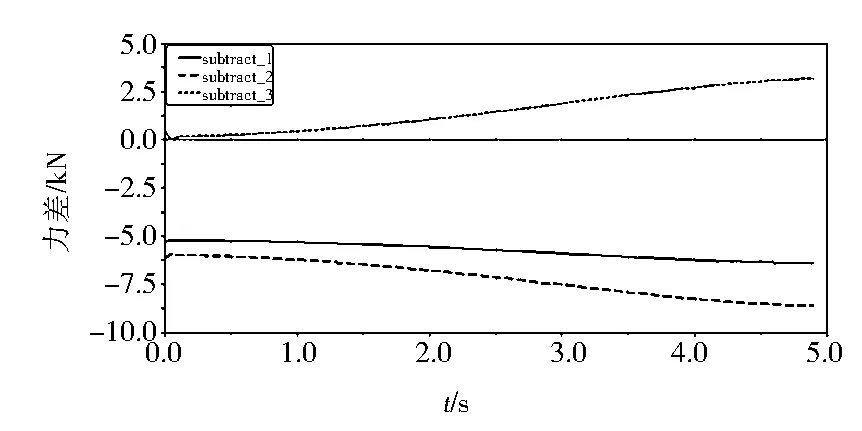
图10 上升工况各铰接点的力差

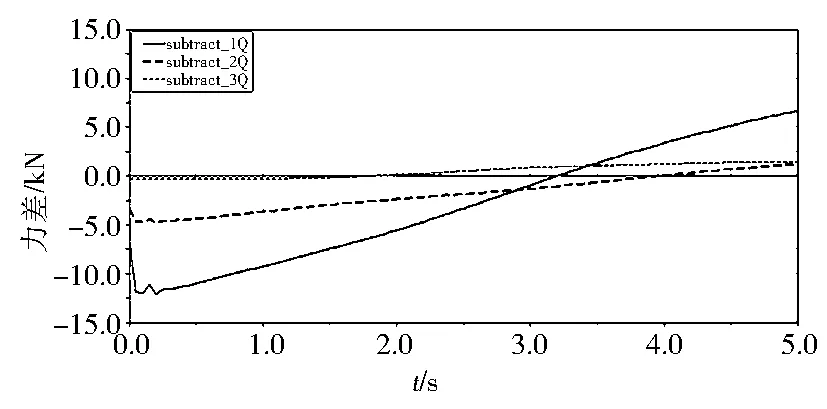
图11 侧倾工况各铰接点的力差

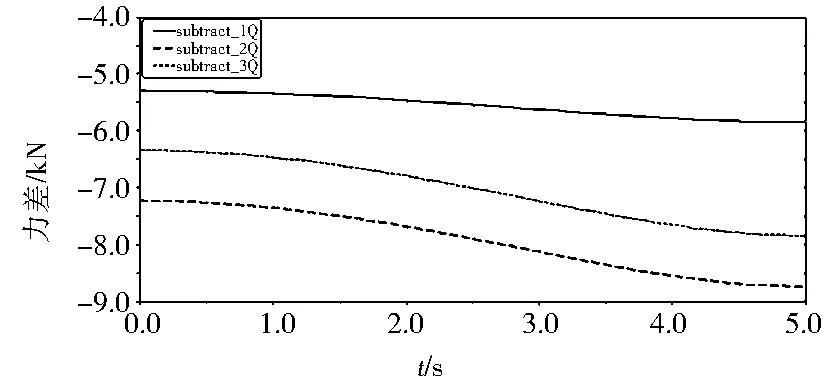
图12 运土前工况各铰接点的力差

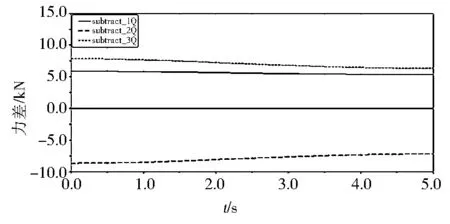
图13 铲土工况各铰接点的力差

分析图10～图13 4个曲线图，比较它们的绝对值大小，发现侧倾工况的subtract_1(推土铲与左右举升缸杆铰接点的力差)在前期仿真过程的绝对值最大，即在推土铲侧倾工况的开始阶段，左右举升缸与推土铲铰接点最易发生破坏.

3 推土机工作装置的优化分析

1)确定优化目标.由前面的分析知，侧倾工况时推土铲与左右举升缸杆铰接点的力差过大易造成机体的破坏，故将优化目标定为该力差绝对值的最大值最小.

2)确定约束条件.由于部件本身的材料刚度要求、装置的作业目的也对模型的结构尺寸提出了要求，因此对以下数据做出约束要求，①液压缸长度的最大伸长量的优化不能超出原来的5%；②举升高度的优化不能超过-5%；③保持装置左右对称点的始终对称性.

3)参数化变量.首先要确定需要优化的部件，部件尺寸的优化表现在关键点的优化上，此模型的可优化点为表1所列的6个点.其中，Point_2和Point_3，Point_6和Point_7，Point_14和Point_15分别是关于纵向对称面(在此模型中是XOY平面)的对称点.可将这6个点的X、Y、Z坐标值参数化为变量，据点的对称性(对称点的XY坐标相等，Z坐标相反)，最终坐标中有9个变量被参数化.由于变量越多工作量越大，故可对它们进行敏感度分析，抛去那些对目标函数影响较小的变量.最终得到5个变量，分别为Point2.X、Point2.Y、Point2.Z、Point14.X、Point14.Y.

表1 需要优化的参考点及其代表的位置

4)优化仿真.利用ADAMS的优化功能，设置相关的优化目标、约束条件、设计变量等，开始优化仿真.

优化迭代的过程如图14所示，系统进行了11次迭代(由于之后的8次迭代的曲线数值数量级很小，所以看起来很接近甚至是重合)，其中圈内部分是局部放大图.观察仿真结果的数据可知，最终优化目标值从11 155.80N变为8 976.72 N，优化效果明显.对该工况的其他力差进行对比，观察图15和图16，结果显示只有推土铲与左右顶推梁铰接点力差的数据略有上升.对优化后的工作装置进行其他工况的仿真分析，发现力差同样都得到了较好的优化，如铲土工况推土铲与左右举升缸铰接点力差的绝对值大小从5 868.49N减小为3 124.21N，与斜撑螺杆及侧倾缸铰接点力差的绝对值大小由8 726.97 N减小为2 303.21N，与左右顶推梁铰接点力差的绝对值由7 862.24N减小为863.47 N，证明此次优化的综合效果比较好.

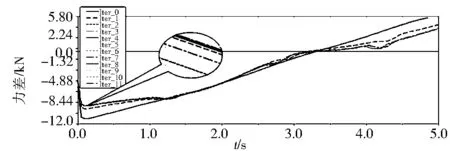
图14 侧倾工况的推土铲与左右举升缸铰接点的力差优化迭代曲线

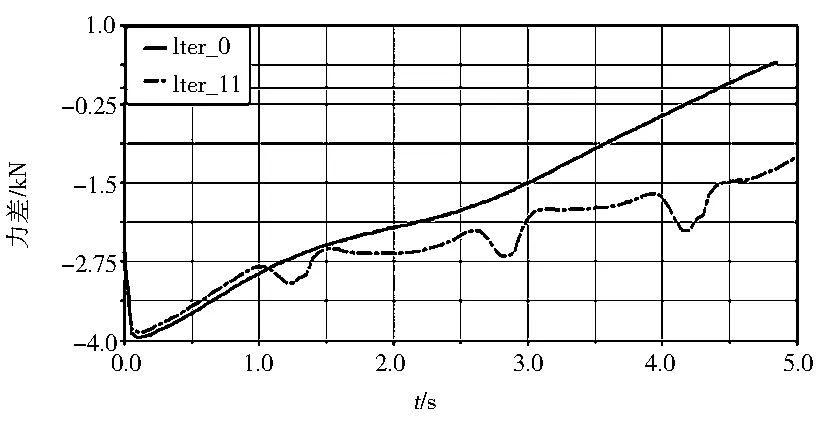
图15 侧倾工况的推土铲与斜撑螺杆及侧倾缸铰接点力差的优化前后对比图

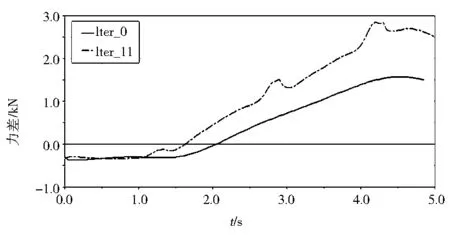
图16 侧倾工况的推土铲与左右顶推梁铰接点的力差优化前后对比图

4 结束语

本文首先分析了推土机工作装置的结构和不同工况下的受力情况，利用ADAMS建立了推土机工作装置的虚拟样机模型，并对四种工况进行仿真分析，结果表明该工作装置的运动情况符合要求，但是左右举升缸与推土铲的铰接点的力差很大.针对结构设计不合理而造成受力不均衡的情况进行了优化改进，改进后的结构性能得到了较大的改善，并提高了构件的安全性且降低了制造成本，具有较高的现实意义.

[1] 乔晓军,李爱峰.浅析国内推土机产业的发展趋势. [J].机械管理开发, 2011(4)：95-96.

[2] 周之胜.推土机行业技术发展与现状. [J].建筑机械化, 2005(10)：38-39.

[3] 林晓磊,符长会.基于ADAMS的推土机工作装置失效分析[J].煤矿机械, 2011，32(5)：98-100.

[4] 叶兰成.大型推土机工作装置仿真分析及结构强度研究[D].长春：吉林大学, 2008.

[5] 赵雪莉.大马力推土机前工作装置结构及性能优化研究[D].长春：吉林大学,2013.

[6] 岳国栋.推土机工作装置的多学科设计优化研究[D].杭州：浙江大学,2009.

[7] 徐东云.轮式推土机工作装置的结构及工作原理[J].建筑机械化, 2004(4)：60-61.