一类奇异Liénard系统的鸭环的存在唯一性

尚德生

(山东理工大学 理学院， 山东 淄博 255091)

在文献[1-2]中，作者利用Blow-up等技巧讨论了在函数F(x)满足什么条件，下面的奇异摄动Liénard系统

会有鸭环存在，其中F(x)是光滑函数，ε>0是个小参数，λ>0而且系统(L)的鸭环的个数可以由系统的慢散度积分

(1)

的零点来衡量，其中Ω是经过 (0,Y)的快轨道的两个端点(x1(Y),Y),(x2(Y),Y)之间的部分慢轨道，如图1所示.

具体结论是

引理1如果F(x)是一个Morse函数，而系统(L)以原点(0,0)为转点，且满足F(0)=0,F′(0)=0,F″(0)≠0，则系统(L)的环性可以由前面的慢散度积分(1)的零点的个数来确定，且其鸭环的稳定性可以由I(Y,λ)关于Y的导数的符号来确定.

图1 系统(L)在ε=0时的轨迹示意图

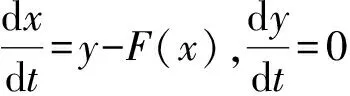
(2)由含有快轨道和慢轨道一起构成的闭曲线环称为系统(L)的一个快慢环(Slow-Fast Cycle)，也称为鸭环(Canard Cycle).

(3)系统(L)的一个鸭环与前面的慢散度积分的一个零点相对应，且其稳定性与I(Y)的导数的相应，即当I(Y)=0,I′(Y)<0时，对应于系统(L)的一个过 (0,Y)的稳定的鸭环，当I(Y)=0,I′(Y)>0时，对应于系统(L)的一个过 (0,Y)的不稳定的鸭环.

下面对一种特殊的Morse函数F(x)，来讨论系统(L)的环性，这里取

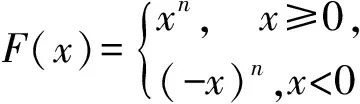
在区间(0,λ)∪(λ,+∞)上的零点即可.

注意到G(0)=0;当z→λ时，G(z)→-∞;且z→+∞时，G(z)→+∞.

又因为

G′(z)=z2n-4+λ2z2n-6+…+

显然，当z∈(λ,+∞)时，有G′(z)>0，即G(z)在区间(λ,+∞)单调递增.但是当z∈(0,λ)时，容易得到

从而G(z)单调递减，亦即有G(z)0，如图2所示.

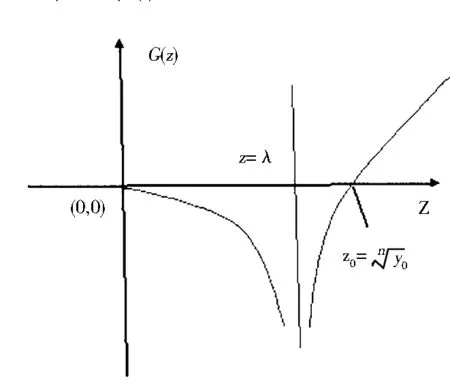
图2 G(Z)的图形示意图

从而系统(L)在(0,+∞)上有且只有一个鸭环，且该鸭环是不稳定的，它包含系统(L)的唯一奇点(λ,F(λ)).另一方面，可以得到在该奇点处系统(L)的散度为

div(L)=-F′(λ)=-nλn-1<0

即系统的这个唯一奇点是稳定的焦点，这也说明这个唯一的鸭环是不稳定的.由此得到下面的结论.

定理1对于任意的正整数n≥2相应的函数F(x)，奇异摄动系统(L)在整个xoy-平面上有且只有唯一一个不稳定的鸭环存在，此鸭环包含系统的唯一稳定的有限远奇点(λ,F(λ)).

[1] Dumortier F, Roussarie R. Canard cycles and center manifolds[J]. Memoirs of Amer. Math. Soc, 1996,121:1-100.

[2] De Maesschalck P, Dumortier F. Singular perturbations and vanishing passage through a turning point[J]. Differential Equations,2010,248(9):2 294-2 328.